4.1: Una introducción a los conjuntos

Un conjunto es una colección de objetos. Los objetos de un conjunto se denominan sus elementos o miembros. Los elementos de un conjunto pueden ser cualquier tipo de objetos, ¡incluidos los conjuntos! Los miembros de un conjunto ni siquiera tienen que ser del mismo tipo. Por ejemplo, aunque puede que no tenga ninguna aplicación significativa, un conjunto puede consistir en números y nombres.

Usualmente usamos letras mayúsculas como\(A\),\(B\),\(C\),\(S\), y\(T\) para representar conjuntos, y denotar sus elementos genéricos por sus correspondientes letras minúsculas\(a\),\(b\),\(c\),\(s\), y\(t\), respectivamente. Para indicar que\(b\) es un elemento del conjunto\(B\), adoptamos la notación\(b\in B\), que significa “\(b\)pertenece a\(B\)” o “\(b\)es un elemento de”\(B\). También escribimos\(B\mathbb{N}i b\), y decimos “\(B\)contiene\(b\) (como un elemento)”.

Designamos estas notaciones para algunos conjuntos especiales de números:\[\begin{array}{c c l} \mathbb{R} &=& \mbox{the set of real numbers}, \\ \mathbb{Q} &=& \mbox{the set of rational numbers}, \\ \mathbb{Z} &=& \mbox{the set of integers}, \\ \mathbb{N} &=& \mbox{the set of natural numbers (positive integers)}. \end{array} \nonumber\] Todos estos son conjuntos infinitos, porque todos contienen infinitamente muchos elementos. En contraste, los conjuntos finitos contienen finitamente muchos elementos.

Podemos usar el método roster para describir un conjunto si solo tiene un pequeño número de elementos. Enumeramos todos sus elementos explícitamente, como en\[A = \mbox{the set of natural numbers not exceeding 7} = \{1,2,3,4,5,6,7\}. \nonumber\] Para conjuntos con más elementos, mostramos las primeras entradas para mostrar un patrón, y usamos puntos suspensivos para indicar “y así sucesivamente”. Por ejemplo,\[\{1,2,3,\ldots,20\} \nonumber\] representa el conjunto de los primeros 20 enteros positivos. El patrón de repetición se puede extender indefinidamente, como en\[\begin{array}{c c l} \mathbb{N} &=& \{1,2,3,\ldots\} \\ \mathbb{Z} &=& \{\ldots,-2,-1,0,1,2,\ldots\} \end{array} \nonumber\] Hay tres tipos de enteros: positivo, negativo, y el número entero sin signo cero. En lo que respecta a la paridad, un entero es par o impar. Un entero es par si y solo si es divisible por dos. Por lo tanto, el conjunto de enteros pares se puede describir como\(\{\ldots,-4,-2,0,2,4,\ldots\}\).

Podemos usar una notación set-builder para describir un conjunto. Por ejemplo, el conjunto de números naturales se define como\[\mathbb{N} = \{x\in\mathbb{Z} \mid x>0 \}. \nonumber\] Aquí, la barra vertical\(\mid\) se lee como “tal que” o “para cuál”. De ahí que el lado derecho de la ecuación se pronuncia como “el conjunto de\(x\) pertenecer al conjunto de enteros tal que”\(x>0\), o simplemente “el conjunto de enteros\(x\) tal que”\(x>0\). En general, este método descriptivo aparece en el formato\[\{\,\mbox{membership}\;\mid\;\mbox{properties}\,\}. \nonumber\] La notación\(\mid\) significa “tal que” o “para cuál” sólo cuando se utiliza en la notación establecida. Puede significar otra cosa en un contexto diferente. Por lo tanto, no escribas “deja\(x\) ser un número real\(\mid\)\(x^2>3\)” si quieres decir “deja\(x\) ser un número real tal que”\(x^2>3\). Se considera impropio usar una notación matemática como abreviatura.

Ejemplo\(\PageIndex{1}\label{eg:setintro-01}\)

Escribe estos dos conjuntos\[\{x\in\mathbb{Z} \mid x^2 \leq 1\} \quad\mbox{and}\quad \{x\in\mathbb{N} \mid x^2 \leq 1\} \nonumber\] enumerando sus elementos explícitamente.

Contestar

El primer conjunto tiene tres elementos, y es igual\(\{-1,0,1\}\). El segundo conjunto es un conjunto singleton; es igual a\(\{1\}\).

ejercicio práctico\(\PageIndex{1}\label{he:setintro-01}\)

Utilice el método de lista para describir los conjuntos\(\{x\in\mathbb{Z} \mid x^2\leq20\}\) y\(\{x\in\mathbb{N} \mid x^2\leq20\}\).

ejercicio práctico\(\PageIndex{2}\label{he:setintro-02}\)

Usar el método de lista para describir el conjunto\[\{x\in\mathbb{N} \mid x\leq20 \mbox{ and $x=n^2$ for some integer $n$}\}. \nonumber\]

Hay un formato ligeramente diferente para la notación set-builder. Antes de la barra vertical, describimos la forma que asumen los elementos, y después de la barra vertical, indicamos de dónde vamos a recoger estos elementos:\[\{\,\mbox{pattern}\;\mid\;\mbox{membership}\,\}. \nonumber\] Aquí la barra vertical\(\mid\) significa “dónde”. Por ejemplo,\[\{ x^2 \mid x\in\mathbb{Z} \} \nonumber\] es el conjunto de\(x^2\) dónde\(x\in\mathbb{Z}\). Representa el conjunto de cuadrados:\(\{0,1,4,9,16,25,\ldots\}\).

Ejemplo\(\PageIndex{2}\label{eg:setintro-02}\)

El conjunto\[\{ 2n \mid n\in\mathbb{Z} \} \nonumber\] describe el conjunto de números pares. También podemos escribir el conjunto como\(2\mathbb{Z}\).

ejercicio práctico\(\PageIndex{3}\label{he:setintro-03}\)

Describa el conjunto\(\{2n+1 \mid n\in\mathbb{Z}\}\) con el método de roster.

ejercicio práctico\(\PageIndex{4}\label{he:setintro-04}\)

Utilice el método de lista para describir el conjunto\(\{3n \mid n\in\mathbb{Z}\}\).

Un intervalo es un conjunto de números reales, todos los cuales se encuentran entre dos números reales. Si se incluyen o excluyen los puntos finales depende de si el intervalo es abierto, cerrado o semiabierto. Adoptamos la siguiente notación de intervalo para describirlos:\[\displaylines{ (a,b) = \{x\in\mathbb{R} \mid a < x < b \}, \cr [a,b] = \{x\in\mathbb{R} \mid a\leq x\leq b \}, \cr [a,b) = \{x\in\mathbb{R} \mid a\leq x < b \}, \cr (a,b] = \{x\in\mathbb{R} \mid a < x\leq b \}. \cr} \nonumber\] Se entiende que\(a\) debe ser menor o igual a\(b\). De ahí que la notación\((5,3)\) no tenga mucho sentido. ¿Qué tal\([3,3]\)? ¿Es una notación legítima?

Un intervalo contiene no solo enteros, sino todos los números entre los dos puntos finales. Por números, nos referimos a números enteros y números decimales. Por ejemplo,\((1,5) \neq \{2,3,4\}\) porque el intervalo\((1,5)\) también incluye números decimales como at\(1.276\),\(\sqrt{2}\), y\(\pi\).

Podemos usar\(\pm\infty\) en la notación de intervalo:\[\begin{array}{r c l} (a,\infty) &=& \{ x\in\mathbb{R} \mid a<x \}, \\ (-\infty,a) &=& \{ x\in\mathbb{R} \mid x<a \}. \end{array} \nonumber\] Sin embargo, no podemos escribir\((a,\infty]\) o\([-\infty,a)\), porque no\(\pm\infty\) son números. Es una tontería decir\(x\leq\infty\) o\(-\infty\leq x\). Por la misma razón, podemos escribir\([a,\infty)\) y\((-\infty,a]\), pero no\([a,\infty]\) o\([-\infty,a]\).

Ejemplo\(\PageIndex{3}\label{eg:setintro-03}\)

Escribir los intervalos\((2,3)\),\([2,3]\), y\((2,3]\) en la forma descriptiva.

Solución

De acuerdo con la definición de intervalo, encontramos\[\begin{array}{c c l} {(2,3)} &=& \{x\in\mathbb{R} \mid 2<x<3\}, \\ {[2,3]} &=& \{x\in\mathbb{R} \mid 2\leq x\leq 3\}, \\ {(2,3]} &=& \{x\in\mathbb{R} \mid 2 < x\leq 3\}. \end{array} \nonumber\] ¿Qué dirías de\([2,3)\)?

Ejemplo\(\PageIndex{4}\label{eg:setintro-04}\)

Escribe estos conjuntos\[\{x\in\mathbb{R} \mid -2 \leq x < 5\} \quad\mbox{and}\quad \{x\in\mathbb{R} \mid x^2 \leq 1\} \nonumber\] en forma de intervalo.

Solución

Las respuestas son\([-2,5)\) y\([-1,1]\), respectivamente. La membresía de\(x\) afecta las respuestas. Si cambiamos el segundo set a\(\{x\in\mathbb{Z} \mid x^2\leq 1\}\), la respuesta habría sido\(\{-1,0,1\}\). ¿Puedes explicar por qué\(\{-1,0,1\} \neq [-1,1]\)?

Ejemplo\(\PageIndex{5}\label{eg:setintro-05}\)

Asegúrate de que estás usando los tipos de números correctos. Compara estos dos conjuntos\[\begin{array}{c c l} S &=& \{x\in\mathbb{Z} \mid x^2 \leq 5 \}, \\ T &=& \{x\in\mathbb{R} \mid x^2 \leq 5 \}. \end{array} \nonumber\] Uno consiste únicamente en enteros, mientras que el otro contiene números reales. Así,\(S=\{-2,-1,0,1,2\}\), y\(T=\big[-\sqrt{5},\sqrt{5}\,\big]\).

ejercicio práctico\(\PageIndex{5}\label{he:setintro-05}\)

¿Cuál de los siguientes conjuntos\[\{x\in\mathbb{Z} \mid 1<x<7\} \quad\mbox{and}\quad \{x\in\mathbb{R} \mid 1<x<7\} \nonumber\] puede ser representado por la notación de intervalo\((1,7)\)? Explique.

ejercicio práctico\(\PageIndex{6}\label{he:setintro-06}\)

Explique por qué\([2,7\,] \neq\{2,3,4,5,6,7\}\).

ejercicio práctico\(\PageIndex{7}\label{he:setintro-07}\)

Verdadero o falso:\((-2,3)=\{-1,0,1,2\}\)? Explique.

Dejar\(S\) ser un conjunto de números; definimos\[\begin{array}{c c l} S^+ &=& \{ x\in S \mid x>0 \}, \\ S^- &=& \{ x\in S \mid x<0 \}, \\ S^* &=& \{ x\in S \mid x \neq 0 \}. \end{array} \nonumber\] En inglés simple,\(S^+\) es el subconjunto de\(S\) contener solo aquellos elementos que son positivos,\(S^-\) contiene solo los elementos negativos de\(S\), y\(S^*\) contiene solo los elementos distintos de cero de\(S\).

Ejemplo\(\PageIndex{6}\label{eg:setintro-06}\)

Eso debería ser obvio\(\mathbb{N}=\mathbb{Z}^+\).

ejercicio práctico\(\PageIndex{8}\label{he:setintro-08}\)

¿Cuál es la notación para el conjunto de enteros negativos?

Algunos matemáticos también adoptan estas notaciones:\[\begin{aligned} bS &=& \{ bx \mid x\in S \}, \\ a+bS &=& \{ a+bx \mid x\in S \}. \end{aligned} \nonumber\] En consecuencia, podemos escribir el conjunto de enteros pares como\(2\mathbb{Z}\), y el conjunto de enteros impares puede ser representado por\(1+2\mathbb{Z}\).

Un conjunto vacío es un conjunto que no contiene ningún elemento. Ambos\[\{x\in\mathbb{R} \mid x>0 \mbox{ and } x<0\} \qquad\mbox{and}\qquad \{x\in\mathbb{R} \mid x^2 < 0\} \nonumber\] son ejemplos de conjuntos vacíos. El segundo ejemplo ilustra una aplicación típica de un conjunto vacío. Proporciona una manera conveniente de declarar que un problema no tiene solución: decimos que el conjunto de soluciones es un conjunto vacío. Denotamos un conjunto vacío con la notación\(\emptyset\) o\(\{\,\}\). Por ejemplo, ¿puedes explicar por qué\((3,3)=\emptyset\)?

ejercicio práctico\(\PageIndex{9}\label{he:setintro-09}\)

¿Qué\([7,7\,]\) significa la notación? ¿Cómo describirías los conjuntos\((7,7)\),\((7,7\,]\) y\([7,7)\)?

Ejemplo\(\PageIndex{7}\label{eg:setintro-07}\)

Determinar cuáles de estas afirmaciones son verdaderas. \[\begin{aligned} \{x\in\mathbb{R} \mid (x^2+2)(x^2+3) = 0\} &=& \emptyset, \\ \{x\in\mathbb{Z} \mid (x^2-2)(x^2+3) = 0\} &=& \emptyset, \\ \{x\in\mathbb{R} \mid (x^2-2)(x^2+3) = 0\} &=& \emptyset, \\ \{x\in\mathbb{R} \mid (x^2-2)(x^2+3)\geq0\} &=& \emptyset. \end{aligned} \nonumber\]

Solución

Las respuestas son: verdadera, verdadera, falsa y falsa, respectivamente.

Ejemplo\(\PageIndex{8}\label{eg:setintro-08}\)

Cuando escribimos\(3,4,5,\ldots,n\), nos estamos refiriendo a una lista de enteros entre 3 y\(n\), inclusive. Se entiende eso\(n\geq3\). En consecuencia, el conjunto\[\{3,4,5,\ldots,n\} \nonumber\] está vacío cuando\(n=2\).

Dos conjuntos\(A\) y\(B\) se dice que son iguales si contienen la misma colección de elementos. De manera más rigurosa, definimos\[A = B \Leftrightarrow \forall x \, (x \in A \Leftrightarrow x \in B). \nonumber\] Dado que los elementos de un conjunto pueden ser conjuntos, tenga precaución y use la notación adecuada cuando compare el contenido de dos conjuntos.

Ejemplo\(\PageIndex{9}\label{eg:setintro-09}\)

Explique por qué\(\big\{0,\{1\}\big\} \neq \{0,1\}\).

Solución

El conjunto\(\big\{0,\{1\}\big\}\) consta de dos elementos: el entero\(0\) y el conjunto\(\{1\}\). El conjunto\(\{0,1\}\) también consta de dos elementos, ambos enteros; es decir, 0 y 1.

Puede que le resulte útil la siguiente analogía. Imagina que un set es una caja. Abres una caja para ver su contenido. La caja en sí se puede comparar con las llaves\(\{\) y\(\}\). Lo que sostiene es exactamente lo que llamamos los elementos del conjunto que representa. El contenido de los dos conjuntos\(\big\{0,\{1\}\big\}\) y\(\{0,1\}\) se representan en los recuadros mostrados en la Figura\(\PageIndex{1}\).

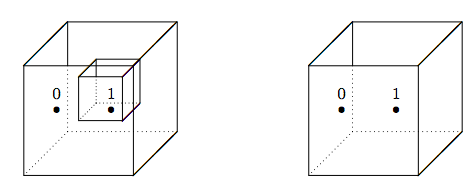
Figura\(\PageIndex{1}\): Los dos conjuntos\(\big\{0,\{1\}\big\}\) y\({0,1}\).

Cuando abres la primera caja, encuentras dos artículos. Uno de ellos es el número 0; el otro es otro cuadro que contiene el número 1. La segunda caja también contiene dos elementos que son ambos números. Lo que encuentras en estas dos cajas no es lo mismo. De ahí que los conjuntos que representan sean diferentes.

ejercicio práctico\(\PageIndex{10}\label{he:setintro-10}\)

Nombra algunas diferencias entre los conjuntos\(\big\{0,\{1\}\big\}\) y\(\big\{\{0\},\{1\}\big\}\).

Ejemplo\(\PageIndex{10}\label{eg:setintro-10}\)

Verdadero o falso:\(\mathbb{Z}=\big\{\{\ldots,-3,-2,-1\},0,\{1,2,3,\ldots\}\big\}\)?

Solución

El conjunto de la izquierda es\(\mathbb{Z}\), y\[\mathbb{Z} = \{\ldots,-3,-2,-1,0,1,2,3,\ldots\}. \nonumber\] es un conjunto infinito. El conjunto de la derecha consta de solo tres elementos:

1. el conjunto\(\{\ldots,-3,-2,-1\}\), que es el conjunto de enteros negativos,
2. el entero 0, y
3. el conjunto\(\{1,2,3,\ldots\}\), que es el conjunto de enteros positivos.

De ahí que no sean iguales. Observe que\[\mathbb{Z} \neq \big\{\{\ldots,-3,-2,-1\}, \{0\}, \{1,2,3,\ldots\}\big\} \nonumber\] tampoco, porque el conjunto de la derecha es un conjunto de tres conjuntos, mientras que el conjunto de la izquierda es un conjunto de enteros. Uno tiene tres elementos; el otro tiene infinitamente muchos elementos.

Para reducir la confusión, en lugar de decir un conjunto de conjuntos, podríamos decir una colección de conjuntos o una familia de conjuntos. Por ejemplo,\[\big\{\{1,3,5,\ldots,\}, \{2,4,6,\ldots\,\}\big\} \nonumber\] es una familia de dos conjuntos, uno de los cuales es el conjunto de enteros impares positivos; el otro es el conjunto de enteros pares positivos.

Definición

Se dice que un conjunto es finito si tiene un número finito de elementos. El número de elementos en un conjunto finito\(A\) se llama su cardinalidad, y se denota por\(|A|\). De ahí\(|A|\) que, siempre sea no negativo. Si\(A\) es un conjunto infinito, algunos autores escribirían\(|A|=\infty\).

Ejemplo\(\PageIndex{11}\label{eg:setintro-11}\)

Si bien es trivial eso\(|\{1,4,7,8\}| = 4\), y\(|\{0,1\}| = 2\), puede que no sea obvio que\[\big|\big\{0,\{1\}\big\}\big| = 2, \nonumber\] y\[\big|\big\{\{\ldots,-3,-2,-1\},0,\{1,2,3,\ldots\,\}\big\}| = 3. \nonumber\] lo que importa es el número de entradas en un conjunto, que se puede comparar con la cantidad de artículos que puedes encontrar al abrir una caja. Aquí hay otro ejemplo:\[|\{x\in\mathbb{R} \mid x^2=9\}| = 2 \nonumber\] porque la ecuación\(x^2=9\) tiene dos soluciones reales. ¿Qué es\(|\{x\in\mathbb{N} \mid x^2=9\}|\)?

ejercicio práctico\(\PageIndex{11}\label{he:setintro-11}\)

Determinar estas cardinalidades:

1. \(|\{x\in\mathbb{Z} \mid x^2-7x-6=0\}|\)
2. \(|\{x\in\mathbb{R} \mid x^2-x-12<0\}|\)
3. \(|\{x\in\mathbb{Z} \mid \mbox{ x is prime and x is even}\}|\)

Recuerda que tus respuestas deben ser no negativas.

ejercicio práctico\(\PageIndex{12}\label{he:setintro-12}\)

Explique por qué es incorrecto decirlo\(|\emptyset|=\emptyset\). De hecho, es una tontería decirlo\(|\emptyset|=\emptyset\). Explique. ¿Cuál debería ser el valor de\(|\emptyset|\)?

Cerramos esta sección con una observación importante sobre los conjuntos. De la definición de igualdad de conjuntos se desprende que no contamos los elementos repetidos como elementos separados. Por ejemplo, supongamos que un pequeño club estudiantil tiene tres oficiales:

silla:	María,
vicepresidenta:	Juan,
secretario:	Juan;

y que\(A\) representen el conjunto de sus funcionarios, y\(B\) el conjunto de posiciones en su junta ejecutiva, entonces\(|A|=2\) y\(|B|=3\), porque\[A = \{ \mbox{Mary}, \mbox{John} \}, \nonumber\] y\[B = \{ \mbox{chair}, \mbox{vice chair}, \mbox{secretary}\}. \nonumber\]

Ejemplo\(\PageIndex{12}\label{eg:setintro-12}\)

Encuentra los errores en la siguiente declaración:\[|\{-2,2\}| = \{\,|-2|,|2|\} = \{2\} = 2, \nonumber\] y corríjalos.

Solución

Esta declaración contiene varios errores. El primer error es asumir que podemos distribuir los símbolos de “valor absoluto”\(|\quad|\) sobre el contenido de un conjunto:\[|\{-2,2\}| \neq \{\,|-2|,|2|\}. \nonumber\] Después de todo, las dos barras verticales no significan valor absoluto en este caso. En cambio, significa la cardinalidad del conjunto\(\{-2,2\}\). De ahí,\(|\{-2,2\}|=2\).

La segunda igualdad\(\{\,|-2|,|2|\} = \{2\}\) es correcta. Después de tomar valores absolutos, ambas entradas se convierten en 2. Sin embargo, no escribimos\(\{|-2|,|2|\} = \{2,2\}\), porque un conjunto no debe contener repetición. Por lo tanto, es correcto decirlo\(\{\,|-2|,|2|\} = \{2\}\).

La última igualdad\(\{2\}=2\) está equivocada. No podemos comparar un conjunto con un número. Imagínese el conjunto\(\{2\}\) como una caja que contiene solo un objeto, y ese objeto es el número 2. En contraste, 2 en el lado derecho se deja al aire libre sin ningún tipo de contención. Eso es claro\(\{2\} \neq 2\).

Todo el enunciado contiene múltiples errores; algunos de ellos son errores sintácticos mientras que otros son conceptuales. Sin embargo, sí tenemos\(|\{-2,2\}|=2\). Si bien la respuesta final es correcta, el argumento utilizado para obtenerla no lo es.

En algunas situaciones, sí queremos contar los elementos repetidos como elementos separados, como en\(S=\{1,2,2,2,3,3,4,4\}\). Llamamos a tal colección un multiset en lugar de un conjunto ordinario. En este caso,\(|S|=8\).

Resumen y revisión

• Un conjunto es una colección de objetos (sin repeticiones).
• Para describir un conjunto, enumere todos sus elementos explícitamente o utilice un método descriptivo.
• Los intervalos son conjuntos de números reales.
• Los elementos de un conjunto pueden ser cualquier tipo de objeto, incluidos los conjuntos.
• Incluso podemos tener un conjunto que contenga elementos diferentes. En particular, podemos mezclar elementos y conjuntos dentro de un conjunto.
• Si un conjunto\(A\) es finito, su cardinalidad\(|A|\) es el número de elementos que contiene. En consecuencia, siempre\(|A|\) es no negativo.

Ejercicios 4.1

Ejercicio\(\PageIndex{1}\label{ex:setintro-01}\)

Escribe cada uno de estos conjuntos enumerando sus elementos explícitamente (es decir, usando el método roster).

1. \(\{n\in\mathbb{Z} \mid -6<n<4\}\)
2. \(\{n\in\mathbb{N} \mid -6<n<4\}\)
3. \(\{x\in\mathbb{Q} \mid x^3-x^2-6x=0\}\)
4. \(\{x\in\mathbb{Q} \mid x^4-11x^2+18=0\}\).

Ejercicio\(\PageIndex{2}\label{ex:setintro-02}\)

Utilice el método de lista para describir estos conjuntos:

1. \(\{x\in\mathbb{N} \mid \mbox{ x<20 and x is a multiple of 3 }\}\)
2. \(\{x\in\mathbb{Z} \mid \mbox{ |x|<20 and x is a multiple of 3 or a multiple of 5 }\}\)
3. \(\{x\in\mathbb{Z} \mid \mbox{ |x|<20 and x is a multiple of 3 and a multiple of 5}\}\)
4. \(\{x\in\mathbb{N} \mid \mbox{ x<20 and x is a multiple of 3 but not a multiple of 5}\}\)

Ejercicio\(\PageIndex{3}\label{ex:setintro-03}\)

Escriba cada uno de los siguientes conjuntos en el formulario\(\{n\in\mathbb{Z} \mid p(n)\}\) con una declaración lógica\(p(n)\) que describa la propiedad de\(n\).

1. \(\{\ldots,-3,-2,-1\}\)
2. \(\{\ldots,-27,-8,-1,0,1,8,27,\ldots\}\)
3. \(\{0,1,4,9,16,\ldots\}\)
4. \(\{\ldots,-15,-10,-5,0,5,10,15,\ldots\}\)
5. \(\{0,4,8,12,\ldots\}\)
6. \(\{\ldots,-14,-8,-2,4,10,16,\ldots\}\)

Ejercicio\(\PageIndex{4}\label{ex:setintro-04}\)

Repite el problema anterior, pero escribe los conjuntos en el formulario\(\{ f(n) \mid n\in S\}\), donde\(f(n)\) hay una fórmula que describe el patrón de los elementos, y\(S\) es un conjunto apropiado de números.

Ejercicio\(\PageIndex{5}\label{ex:setintro-05}\)

Siempre que sea posible, exprese los conjuntos en Problema 3 en la forma\(S^+\)\(S^-\)\(bS\),, o\(a+bS\) para algún conjunto apropiado\(S\).

Ejercicio\(\PageIndex{6}\label{ex:setintro-06}\)

Determine si los siguientes conjuntos son conjuntos vacíos, finitos o infinitos:

1. \(\{2n+1 \mid n\in\mathbb{N}\}\)
2. \(\{x\in\mathbb{R} \mid x^2<0\}\)
3. \(\{x\in\mathbb{Q} \mid x\geq0 \mbox{ and } x\leq0\}\)
4. \(\{x\in\mathbb{N} \mid x<0 \mbox{ or } x>0\}\)

Ejercicio\(\PageIndex{7}\label{ex:setintro-07}\)

Escribe cada uno de estos conjuntos en la notación de intervalo.

1. \(\{x\in\mathbb{R} \mid -4<x<7\}\)
2. \(\{x\in\mathbb{R} \mid -4<x\leq7\}\)
3. \(\{x\in\mathbb{R}^+\mid -4<x\leq7\}\)
4. \(\{x\in\mathbb{R} \mid -4<x\}\)
5. \(\{x\in\mathbb{R} \mid x\leq6\}\)
6. \(\{x\in\mathbb{R}^-\mid 0\leq x\leq6\}\)

Ejercicio\(\PageIndex{8}\label{ex:setintro-08}\)

¿Es\([-\infty,\infty]\) una notación legítima o correcta? Explique.

Ejercicio\(\PageIndex{9}\label{ex:setintro-09}\)

Evalúe las siguientes expresiones.

1. \(|\{x\in\mathbb{Z} \mid -4<x<7\}|\)
2. \(|\{x\in\mathbb{Z} \mid -4<x\leq7\}|\)
3. \(|\{x\in\mathbb{N} \mid -4<x\leq7\}|\)
4. \(|\{x\in\mathbb{R} \mid x^4-2x^3-35x^2=0\}|\)
5. \(|\{-3,-2,2,3\}|\)
6. \(|\{x\in\mathbb{Q} \mid x^2=3\}|\)

Ejercicio\(\PageIndex{10}\label{ex:setintro-10}\)

Determinar cuáles de las siguientes afirmaciones son verdaderas y cuáles son falsas.

1. \(a\in\{a\}\)
2. \(\{3,5\}=\{5,3\}\)
3. \(\emptyset\in\emptyset\)
4. \(\emptyset=\{\emptyset\}\)
5. \(\{\;\}=\emptyset\)
6. \(\emptyset\in\{\emptyset\}\)

Ejercicio\(\PageIndex{11}\label{ex:setintro-11}\)

Determinar cuáles de las siguientes afirmaciones son verdaderas y cuáles son falsas.

1. \(2\in(2,7)\)
2. \(\sqrt{2}\in(1,3)\)
3. \(\big(\sqrt{5}\,\big)^2\in\mathbb{Q}\)
4. \(-5\in\mathbb{N}\)

Ejercicio\(\PageIndex{12}\label{ex:setintro-12}\)

Dar ejemplos de conjuntos\(A\),\(B\) y\(C\) tal que:

1. \(A\in B\)y\(B\in C\), y\(A \notin C\)
2. \(A\in B\)y\(B\in C\), y\(A\in C\)

Ejercicio\(\PageIndex{13}\label{ex:setintro-13}\)

Determinar si las siguientes declaraciones son correctas o incorrectas sintácticamente. Para aquellos que son sintácticamente correctos, determinar sus valores de verdad; para los que son sintácticamente incorrectos, sugerir formas de arreglarlos.

1. \((3,7\,]=3<x\leq7\).
2. \(\{x\in\mathbb{R}\mid x^2<0\} \equiv \emptyset\).

Ejercicio\(\PageIndex{14}\label{ex:setintro-14}\)

Determinar si las siguientes declaraciones son correctas o incorrectas sintácticamente. Para aquellos que son sintácticamente correctos, determinar sus valores de verdad; para los que son sintácticamente incorrectos, sugerir formas de arreglarlos.

1. \(\frac{7}{4}\in[2,\sqrt{7})\).
2. No existe\(x\) tal que\(x\in\mathbb{R}^+\) y\(\mathbb{R}^-\).
3. Si\((0,\infty)\), entonces\(x\) es positivo.