4.2: Subconjuntos y Conjuntos de Potencia

Por lo general, consideramos conjuntos que contienen elementos de tipos similares. La colección de todos los objetos bajo consideración se llama el conjunto universal, y se denota\({\cal U}\). Por ejemplo, para los números, el conjunto universal es\(\mathbb{R}\).

Ejemplo\(\PageIndex{1}\label{eg:subsets-geomfig}\)

Los diagramas de Venn son útiles para demostrar la relación de conjunto. Dejar\[\begin{array}{c c l} {\cal U} &=& \mbox{set of geometric figures}, \\ S &=& \mbox{set of squares}, \\ P &=& \mbox{set of parallelogram}, \\ R &=& \mbox{set of rhombuses}, \\ L &=& \mbox{set of rectangles}, \\ C &=& \mbox{set of circles}. \end{array} \nonumber\] Su relación se muestra en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): La relación entre diversos conjuntos de figuras geométricas.

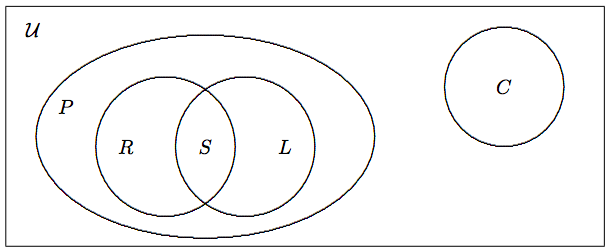
La representación pictórica en la Figura\(\PageIndex{1}\) se denomina diagrama de Venn. Usamos un rectángulo para representar el conjunto universal, y círculos u óvalos para representar los conjuntos dentro del conjunto universal. Las posiciones relativas de estos círculos y óvalos indican la relación de los conjuntos respectivos. Por ejemplo, tener\(R\)\(S\), y\(L\) dentro\(P\) significa que los rombos, los cuadrados y los rectángulos son paralelogramos. En contraste, los círculos son incomparables a los paralelogramos.

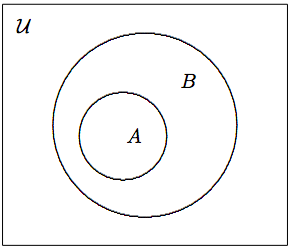
Un conjunto\(A\) es un subconjunto de otro conjunto\(B\), denotado por\(A \subseteq B\), si cada elemento de\(A\) es también un elemento de\(B\). Ver Figura\(\PageIndex{2}\). También llamamos\(B\) un superconjunto de\(A\), y escribimos\(B \supseteq A\), que es similar a\(y\geq x\).

Figura\(\PageIndex{2}\): El diagrama de Venn para\(A \subseteq B\).

Ejemplo\(\PageIndex{2}\label{eg:subsets-02}\)

Es claro que\(\mathbb{N}\subseteq\mathbb{Z}\) y\(\mathbb{Z}\subseteq\mathbb{R}\). Podemos anidar estas dos relaciones en una sola, y escribir\(\mathbb{N}\subseteq\mathbb{Z} \subseteq\mathbb{R}\). De manera más general, tenemos\[\mathbb{N} \subseteq \mathbb{Z} \subseteq \mathbb{Q} \subseteq \mathbb{R}. \nonumber\] Comparar esto con\(x \leq y \leq z \leq w\). Descubriremos muchas similitudes entre\(\subseteq\) y\(\leq\).

Ejemplo\(\PageIndex{3}\label{eg:subsets-03}\)

Es obvio que\[\{1,2,7\} \subseteq \{1,2,3,6,7,9\} \nonumber\] debido a que los tres elementos 1, 2 y 7 del conjunto de la izquierda también aparecen como elementos en el conjunto de la derecha. En tanto,\[\{1,2,7\} \nsubseteq \{1,2,3,6,8,9\} \nonumber\] porque 7 pertenece al primer set pero no al segundo.

Ejemplo\(\PageIndex{4}\label{eg:subsets-04}\)

Las siguientes afirmaciones son ciertas:

1. \(\{1,2,3\}\subseteq \mathbb{N}\).
2. \(\{x\in\mathbb{R} \mid x^2=1\} \subseteq \mathbb{Z}\).

Asegúrese de que puede explicar claramente por qué se mantienen estas relaciones de subconjunto.

ejercicio práctico\(\PageIndex{1}\label{he:subsets-01}\)

¿Estas afirmaciones son verdaderas o falsas?

1. \(\{-1,2\} \nsubseteq \mathbb{N}\), y\(\{-1,2\} \subseteq \mathbb{Z}\).
2. \(\{x\in\mathbb{Z} \mid x^2\leq1\} \subseteq \mathbb{R}\).

Ejemplo\(\PageIndex{5}\label{eg:subsets-05}\)

No asuma que si\(A\nsubseteq B\) entonces debemos tener\(B\subseteq A\). Por ejemplo, si\(A=\{1,5,7\}\) y\(B=\{3,8\}\), entonces\(A \nsubseteq B\); pero también tenemos\(B \nsubseteq A\).

El último ejemplo demuestra que\(A\nsubseteq B\) es más complicado que solo cambiar la notación de subconjuntos como lo hacemos con las desigualdades. Necesitamos una definición más precisa de la relación de subconjunto:

\[A \subseteq B \Leftrightarrow \forall x\in{\cal U} \,(x \in A \Rightarrow x \in B) \nonumber\]

La definición de\(A \subseteq B\).

De ello se deduce que\[A \nsubseteq B \Leftrightarrow \exists x\in{\cal U} \,(x \in A \wedge x \not\in B). \nonumber\] Por lo tanto, para demostrar que no\(A\) es un subconjunto de\(B\), necesitamos encontrar un elemento\(x\) que pertenezca\(A\) pero no\(B\). Hay tres posibilidades; sus diagramas de Venn se representan en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Tres casos de\(A \nsubseteq B\).

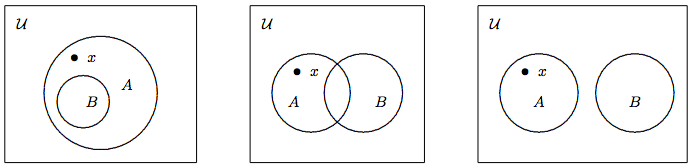
Ejemplo\(\PageIndex{6}\label{eg:subsets-06}\)

Tenemos\([3,6]\subseteq[2,7)\), y\([3,6]\nsubseteq[4,7)\). También tenemos\((3,4) \subseteq [3,4]\).

ejercicio práctico\(\PageIndex{2}\label{he:subsets-02}\)

Verdadero o falso:\([3,4) \subseteq (3,4)\)? Explique.

Con la noción de conjunto universal, ahora podemos afinar la definición de igualdad de conjunto:

\[A = B \Leftrightarrow \forall x\in{\cal U}\,(x\in A \Leftrightarrow x\in B) \nonumber\]

Lógicamente,\(x\in A \Leftrightarrow x\in B\) es equivalente a\[(x\in A \Rightarrow x\in B) \wedge (x\in B\Rightarrow x\in A). \nonumber\] Por lo tanto, también podemos definir la igualdad de conjuntos a través de la relación de subconjunto:

\[A = B \Leftrightarrow (A \subseteq B) \wedge (B \subseteq A) \nonumber\]

que se puede comparar\[x=y \Leftrightarrow (x\leq y) \wedge (y\leq x) \nonumber\] para números reales\(x\) y\(y\).

Esta nueva definición de igualdad de conjunto sugiere que para probarlo\(A=B\), podríamos usar este argumento de dos pasos:

1. \(A \subseteq B\)Demuéstralo.
2. \(B \subseteq A\)Demuéstralo.

Esta técnica es útil cuando es imposible o poco práctico enumerar los elementos de\(A\) y\(B\) para su comparación. Esto es particularmente cierto cuando\(A\) y\(B\) se definen abstractamente. Aplicaremos esta técnica en las próximas secciones.

Los dos se relacionan\(\subseteq\) y\(\leq\) comparten muchas propiedades comunes. La propiedad transitiva es otro ejemplo.

Teorema\(\PageIndex{1}\label{thm:setstrans}\)

Dejar\(A\),\(B\), y\(C\) ser conjuntos. Si\(A\subseteq B\) y\(B\subseteq C\), entonces\(A\subseteq C\).

Discusión

La declaración del teorema es en forma de implicación. Para probarlo\(p\Rightarrow q\), comenzamos con el supuesto\(p\), y lo usamos para demostrar que también\(q\) debe ser cierto. En este caso, estos dos pasos se convierten en

1. Supongamos que\(A\subseteq B\) y\(B\subseteq C\).
2. \(A\subseteq C\)Demuéstralo.

¿Cómo podemos probarlo\(A\subseteq C\)? Sabemos que eso\(A\subseteq C\) significa\[\forall x\in{\cal U}\,(x\in A\Rightarrow x\in C). \nonumber\] Así que tenemos que empezar\(x\in A\), e intentar\(x\in C\) demostrarlo también. ¿Cómo podemos demostrarlo\(x\in C\)? Necesitamos usar la suposición\(A\subseteq B\) y\(B\subseteq C\).

Prueba

Asumir\(A\subseteq B\) y\(B\subseteq C\). Vamos\(x\in A\). Ya que\(A\subseteq B\), también tenemos\(x\in B\). De igual manera,\(B\subseteq C\) implica que\(x\in C\). Dado que cada elemento\(x\) en también\(A\) es un elemento de\(C\), concluimos que\(A\subseteq C\).

La prueba se basa en la definición de la relación de subconjunto. Muchas pruebas en matemáticas son bastante simples si conoces las definiciones subyacentes.

Ejemplo\(\PageIndex{7}\label{eg:subsets-07}\)

Demostrar que\(x \in A \Leftrightarrow \{x\} \subseteq A\), para cualquier elemento\(x\in{\cal U}\)

Discusión

Llamamos a\(p\Leftrightarrow q\) una declaración bicondicional porque consta de dos implicaciones\(p \Rightarrow q\) y\(p\Leftarrow q\). De ahí que tengamos que probarlo en dos pasos:

1. \(p \Rightarrow q\)Demuéstralo.
2. \(q \Rightarrow p\)Demuéstralo.

Llamamos a estas dos implicaciones la necesidad y suficiencia de la declaración bicondicional, y las denotamos (\(\Rightarrow\)) y (\(\Leftarrow\)), respectivamente. En este problema,

• (\(\Rightarrow\)) significa “\(x\in A\Rightarrow\{x\}\subseteq A\)”.
• (\(\Leftarrow\)) significa “\(\{x\}\subseteq A\Rightarrow x\in A\)”.

Así es como puede verse la prueba:

\[\begin{array}{c c c} (\Rightarrow) & \quad \text{ Assume } x\in A. & \qquad\ldots\qquad & \text{Therefore } x \subseteq A. \\ (\Leftarrow) & \quad \text{Assume } x \subseteq A. & \qquad\ldots\qquad & \text{ Therefore } x \in A. \end{array} \nonumber\]

Ahora procedemos a terminar la prueba.

Contestar

(\(\Rightarrow\)) Asumir\(x \in A\). El conjunto\(\{x\}\) contiene solo un elemento\(x\), que también es un elemento de\(A\). Así, cada elemento de\(\{x\}\) es también un elemento de\(A\). Por definición,\(\{x\} \subseteq A\).

(\(\Leftarrow\)) Asumir\(\{x\} \subseteq A\). La definición de la relación de subconjunto afirma que cada elemento de\(\{x\}\) es también un elemento de\(A\). En particular,\(x\) es un elemento de\(\{x\}\), por lo que también es un elemento de\(A\). Por lo tanto,\(x \in A\).

Definición

El conjunto\(A\) es un subconjunto apropiado de\(B\), denotado\(A \subsetneq B\) o\(A \subset B\), si\(A\) es un subconjunto de\(B\), y\(A\neq B\). Simbólicamente,\(A \subset B \Leftrightarrow (A \subseteq B) \wedge (A \neq B)\). Equivalentemente,\[A \subset B \Leftrightarrow (A \subseteq B) \wedge \exists x\in{\cal U}\,(x \in B \wedge x \not\in A). \nonumber\] Ver el diagrama de Venn en la Figura\(\PageIndex{4}\).

Figura\(\PageIndex{4}\): La definición de un subconjunto propio.

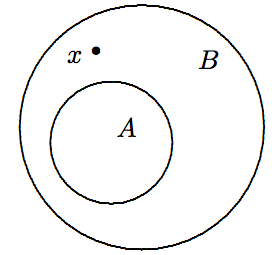
Ejemplo\(\PageIndex{8}\label{eg:subsets-08}\)

Eso es claro\([0,5]\subset\mathbb{R}\). También tenemos\[\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}. \nonumber\] Nota las similitudes entre\(\subset\) y\(<\). Compara la última expresión con\[x < y < z < w. \nonumber\] Aquí hay otra similitud entre\(\subset\) y\(<\). Para los números,\(x<y\) y\(y<z\) juntos implican eso\(x<z\). A esto lo llamamos la propiedad transitiva. De manera similar, para conjuntos, si\(A\subset B\) y\(B\subset C\), entonces\(A\subset C\); véase Teorema\(4.2.1\).

ejercicio práctico\(\PageIndex{3}\label{he:subsets-03}\)

Verdadero o falso:\((3,4)\subset[3,4]\)? ¿Qué tal\((3,4)\subset(3,4]\)?

Teorema\(\PageIndex{2} \label{thm:twosubsets}\)

Para cualquier conjunto\(A\), tenemos\(\emptyset \subseteq A\) y\(A \subseteq A\). En particular,\(\emptyset\subseteq\emptyset\).

Prueba

Dado que cada elemento de\(A\) también aparece en\(A\), se deduce inmediatamente que\(A\subseteq A\). Para demostrarlo\(\emptyset\subseteq A\), necesitamos verificar la implicación\[x\in\emptyset \Rightarrow x\in A \nonumber\] para cualquier arbitrario\(x\in{\cal U}\). Ya que\(\emptyset\) está vacío, siempre\(x\in\emptyset\) es falso; de ahí que la implicación sea siempre verdadera. En consecuencia,\(\emptyset\subseteq A\) para cualquier conjunto\(A\). En particular, cuando\(A=\emptyset\), obtenemos\(\emptyset\subseteq \emptyset\).

Ejemplo\(\PageIndex{9}\label{eg:subsets-09}\)

Determinar los valores de verdad de estas expresiones.

1. \(\emptyset \in \emptyset\)
2. \(1 \subseteq \{1\}\)
3. \(\emptyset \in \{\emptyset\}\)

Contestar

1. Por definición, un conjunto vacío no contiene ningún elemento. En consecuencia, la afirmación\(\emptyset\in\emptyset\) es falsa.
2. Una relación de subconjunto solo existe entre dos conjuntos. A la izquierda del símbolo\(\subseteq\), sólo tenemos un número, que no es un conjunto. De ahí que la afirmación sea falsa. De hecho, esta expresión es sintácticamente incorrecta.
3. El conjunto\(\{\emptyset\}\) contiene un elemento, que resulta ser un conjunto vacío. Compare esto con una caja vacía dentro de otra caja. La caja exterior se describe por el par de soportes establecidos\(\{\,\ldots\,\}\), y la caja (vacía) en el interior es\(\emptyset\). De ello se deduce que\(\emptyset\in\{\emptyset\}\) es una verdadera afirmación.

ejercicio práctico\(\PageIndex{4}\label{he:subsets-04}\)

Determinar los valores de verdad de estas expresiones.

1. \(\emptyset \subseteq \{\emptyset\}\)
2. \(\{1\} \subseteq \big\{1,\{1,2\}\big\}\)
3. \(\{1\} \subseteq \big\{\{1\},\{1,2\}\big\}\)

Definición

El conjunto de todos los subconjuntos de\(A\) se llama el conjunto de potencia de\(A\), denotado\(\wp(A)\).

Dado que un conjunto de potencia en sí mismo es un conjunto, necesitamos usar un par de llaves izquierda y derecha (establecer corchetes) para encerrar todos sus elementos. Sus elementos son en sí mismos conjuntos, cada uno de los cuales requiere su propio par de llaves rizadas izquierda y derecha. En consecuencia, necesitamos al menos dos niveles de corchetes para describir un conjunto de potencia.

Ejemplo\(\PageIndex{10}\label{eg:subsets-10}\)

Dejar\(A=\{1,2\}\) y\(B=\{1\}\). Los subconjuntos de\(A\) son\(\emptyset\),\(\{1\}\),\(\{2\}\) y\(\{1,2\}\). Por lo tanto,\[\wp(A) = \big\{ \emptyset, \{1\}, \{2\}, \{1,2\} \big\}. \nonumber\] de manera similar, encontramos\[\wp(B) = \big\{ \emptyset, \{1\} \big\}. \nonumber\] Podemos escribir directamente\[\wp(\{1,2\}) = \big\{ \emptyset, \{1\}, \{2\}, \{1,2\} \big\}, \qquad\mbox{and}\qquad \wp(\{1\}) = \big\{ \emptyset, \{1\} \big\} \nonumber\] sin introducir letras para representar los conjuntos involucrados.

ejercicio práctico\(\PageIndex{5}\label{he:subsets-05}\)

Evaluemos\(\wp(\{1,2,3,4\})\). Para garantizar que no se pierda ningún subconjunto, enumeramos estos subconjuntos según sus tamaños. Dado que\(\emptyset\) es el subconjunto de cualquier conjunto, siempre\(\emptyset\) es un elemento en el conjunto de potencia. Este es el subconjunto de tamaño 0. A continuación, enumere los subconjuntos singleton (subconjuntos con un solo elemento). Después los subconjuntos de dobletes, y así sucesivamente. Complete la siguiente tabla.

\[\begin{array}{|c|l|} \hline \mbox{size} & \mbox{subsets} \\ \hline 0 & \emptyset \\ 1 & \{1\}, \{2\}, \ldots \qquad \\ 2 & \{1,2\}, \{1,3\}, \ldots \hskip2in \\ 3 & \{1,2,3\}, \ldots \hskip1in \\ 4 & \ldots \\ \hline \end{array} \nonumber\]Ya que\(A\subseteq A\) para cualquier conjunto\(A\), el conjunto de potencia\(\wp(A)\) siempre se contiene a\(A\) sí mismo. En consecuencia, el último subconjunto de la lista debería ser\(A\) él mismo.

Ahora estamos listos para juntarlos para formar el conjunto de poder. Todo lo que necesitas es poner todos los subconjuntos dentro de un par de llaves más grandes (un conjunto de potencia es en sí mismo un conjunto; por lo tanto, necesita un par de llaves en su descripción). Pon tu respuesta final en el espacio de abajo.

Verifique que los tirantes izquierdo y derecho coincidan perfectamente.

Ejemplo\(\PageIndex{11}\label{eg:subsets-11}\)

Ya que\(A\) es un subconjunto de\(A\), pertenece a\(\wp(A)\). No obstante, es impropio decirlo\(A \subseteq \wp(A)\). ¿Puedes explicar por qué? ¿Cuál debería ser la notación correcta?

Contestar

El conjunto de potencia\(\wp(A)\) es la colección de todos los subconjuntos de\(A\). Así, los elementos en\(\wp(A)\) son subconjuntos de\(A\). Uno de estos subconjuntos es el\(A\) propio conjunto. De ahí que,\(A\) sí mismo aparezca como un elemento en\(\wp(A)\), y escribimos\(A\in\wp(A)\) para describir esta membresía.

Esto es diferente a decir eso\(A\subseteq\wp(A)\). Para tener la relación de subconjunto\(A\subseteq\wp(A)\), cada elemento en también\(A\) debe aparecer como un elemento en\(\wp(A)\). Los elementos de\(\wp(A)\) son conjuntos (son subconjuntos de\(A\), y los subconjuntos son conjuntos). Un elemento de no\(A\) es lo mismo que un subconjunto de\(A\). Por lo tanto, aunque\(A\subseteq\wp(A)\) es sintácticamente correcto, su valor de verdad es falso.

ejercicio práctico\(\PageIndex{6}\label{he:subsets-06}\)

Explicar la diferencia entre\(\emptyset\) y\(\{\emptyset\}\). ¿Cuántos elementos hay en\(\emptyset\) y\(\{\emptyset\}\)? ¿Es cierto eso\(\wp(\emptyset) = \{\emptyset\}\)?

Teorema\(\PageIndex{3}\label{thm:powersetcard}\)

Si\(A\) es un conjunto\(n\) -element, entonces\(\wp(A)\) tiene\(2^n\) elementos. En otras palabras, un conjunto\(n\) -element tiene subconjuntos\(2^n\) distintos.

Prueba

¿Cuántos subconjuntos de\(A\) podemos construir? Para formar un subconjunto, pasamos por cada uno de los\(n\) elementos y nos preguntamos si queremos incluir este elemento en particular o no. Dado que hay dos opciones (sí o no) para cada uno de los\(n\) elementos en\(A\), hemos encontrado\(\underbrace{2\cdot2\cdot\cdots2}_{\mbox{n times}}\, =2^n\) subconjuntos.

ejercicio práctico\(\PageIndex{7}\label{he:subsets-07}\)

¿En cuántos elementos hay\(\wp(\{\alpha,\beta, \gamma\})\)? ¿Qué son?

ejercicio práctico\(\PageIndex{8}\label{he:subsets-08}\)

¿De qué es la cardinalidad\(\emptyset\)? ¿Qué tal\(\wp(\emptyset)\)? Describir\(\wp(\emptyset)\).

ejercicio práctico\(\PageIndex{9}\label{he:subsets-09}\)

¿Es correcto escribir\(|\wp(A)|=2^{|A|}\)? ¿Qué tal\(|\wp(A)|=2^A\)? Explique.

Ejemplo\(\PageIndex{12}\label{eg:subsets-12}\)

Cuando un conjunto contiene conjuntos como elementos, su conjunto de potencia podría volverse bastante complicado. Aquí hay dos ejemplos. \[\begin{aligned} \wp(\big\{\{ a\},\{1\}\big\}) &=& \Big\{ \emptyset, \big\{\{a\}\big\}, \big\{\{1\}\big\}, \big\{\{a\},\{1\}\big\} \Big\}, \\ \wp(\big\{\emptyset,\{1\}\big\}) &=& \Big\{ \emptyset, \{\emptyset\}, \big\{\{1\}\big\}, \big\{\emptyset,\{1\}\big\} \Big\}. \end{aligned} \nonumber\]Asegúrese de entender las notaciones utilizadas en estos ejemplos. En particular, examine el número de niveles de corchetes establecidos utilizados en cada ejemplo.

Resumen y revisión

• Un conjunto\(S\) es un subconjunto de otro conjunto\(T\) si y solo si cada elemento en se\(S\) puede encontrar en\(T\).
• En símbolos,\(S\subseteq T \Leftrightarrow \forall x\in{\cal U}\, (x\in S \Rightarrow x\in T)\).
• En consecuencia, para demostrar eso\(S\subseteq T\), tenemos que comenzar con un elemento arbitrario\(x\) en\(S\), y mostrar que\(x\) también le pertenece\(T\).
• La definición de relación de subconjunto implica que para cualquier conjunto\(S\), siempre tenemos\(\emptyset\subseteq S\) y\(S\subseteq S\).
• El conjunto de potencia de un conjunto\(S\), denotado\(\wp(S)\), contiene todos los subconjuntos de\(S\).
• Si\(|S|=n\), entonces\(|\wp(S)|=2^n\). Por lo tanto, un conjunto de\(n\) elementos -tiene\(2^n\) subconjuntos.
• Para construir\(\wp(S)\), enumere los subconjuntos de\(S\) según sus tamaños. Asegúrese de usar un par de llaves para cada subconjunto y encerrarlas todas dentro de un par de llaves exteriores.

Ejercicios 4.2

Ejercicio\(\PageIndex{1}\label{ex:subsets-01}\)

Determinar cuáles de las siguientes afirmaciones son verdaderas y cuáles son falsas.

1. \(\{1,2,3\} \subseteq \{0,1,2,3,4\}\)
2. \(\{1,2,3\} \subseteq \mathbb{N}\)
3. \(\{1,2\} \subset [1,2]\)
4. \([2,4] \subseteq (0,6)\)
5. \([2,4) \subset [2,4]\)
6. \([2,4) \subseteq (2,4]\)

Ejercicio\(\PageIndex{2}\label{ex:subsets-02}\)

Determinar cuáles de las siguientes afirmaciones son verdaderas y cuáles son falsas.

1. \(a \subseteq \{a\}\)
2. \(\{a\} \subseteq \{a,b\}\)
3. \(\emptyset \subseteq \emptyset\)
4. \(\emptyset \subseteq \{\emptyset\}\)
5. \(\emptyset \subset \{\emptyset\}\)
6. \(\{a\} \subseteq \wp(\{\{a\},\{b\}\})\)

Ejercicio\(\PageIndex{3}\label{ex:subsets-03}\)

Explique por qué\(\mathbb{Z} \subseteq \mathbb{Q}\). En particular, explique cómo expresar un entero como un número racional.

Ejercicio\(\PageIndex{4}\label{ex:subsets-04}\)

Verdadero o falso:\(\mathbb{N} \subseteq 6\mathbb{N}\)? Explique.

Ejercicio\(\PageIndex{5}\label{ex:subsets-05}\)

Si\(A\subseteq B\),\(B\subseteq C\), y\(C\subseteq D\), ¿es cierto eso\(A\subseteq D\)? ¿Cómo se llama a esta propiedad?

Ejercicio\(\PageIndex{6}\label{ex:subsets-06}\)

Determine si las siguientes afirmaciones son verdaderas o falsas:

1. El conjunto vacío\(\emptyset\) es un subconjunto de\(\{1,2,3\}\).
2. Si\(A=\{1,2,3\}\), entonces\(\{1\}\) es un subconjunto de\(\wp(A)\).

Ejercicio\(\PageIndex{7}\label{ex:subsets-07}\)

Encuentra el conjunto de potencia de los siguientes conjuntos.

1. \(\{a,b\}\)
2. \(\{4,7\}\)
3. \(\{x,y,z,w\}\)
4. \(\big\{\{a\}\big\}\)
5. \(\big\{ a,\{b\} \big\}\)
6. \(\big\{ \{x\},\{y\} \big\}\)

Ejercicio\(\PageIndex{8}\label{ex:subsets-08}\)

Evalúe los siguientes conjuntos.

1. \(\wp(\{\emptyset\})\)
2. \(\wp(\wp(\{a,b\}))\)
3. \(\wp(\wp(\wp(\emptyset)))\)

Ejercicio\(\PageIndex{9}\label{ex:subsets-09}\)

Eso lo hemos aprendido\(A\subseteq A\) para cualquier set\(A\). Entonces, ¿deberíamos escribir\(A\in\wp(A)\) o\(A\subseteq\wp(A)\)? Explique.

Ejercicio\(\PageIndex{10}\label{ex:subsets-10}\)

Demostrar que\(X\in\wp(A)\) si y sólo si\(X\subseteq A\).

Ejercicio\(\PageIndex{11}\label{ex:subsets-11}\)

Determinar cuáles de las siguientes afirmaciones son verdaderas y cuáles son falsas. ¡Explique!

1. \(\{a\}\in \{a,b,c\}\)
2. \(\{a\}\subseteq\{\{a\},b,c\}\)
3. \(\{a\}\in \wp(\{\{a\},b,c\})\)

Ejercicio\(\PageIndex{12}\label{ex:subsets-12}\)

Determinar cuáles de las siguientes afirmaciones son verdaderas y cuáles son falsas. ¡Explique!

1. \(\{a\}\subseteq\{a,b,c\}\)
2. \(\{a\}\subseteq\{\{a,b\},c\}\)
3. \(\{a\}\subseteq\wp(\{\{a\},b,c\})\)