7.1: Definición de Relaciones

Dados dos conjuntos no vacíos\(A\) y\(B\), una función nos dice cómo obtener un elemento único a\(b\in B\) partir de cualquier elemento\(a\in A\). Muy a menudo, sólo nos interesa algún tipo de relación entre los elementos de estos dos conjuntos. Un ejemplo familiar es la igualdad de dos números. Al decir\(a=b\), estamos proclamando que los dos números\(a\) y\(b\) están relacionados por ser iguales en valor. De igual manera,\(a\geq b\) es otro ejemplo de una relación.

Ejemplo\(\PageIndex{1}\label{eg:defnrelat-01}\)

Dado\(a, b\in\mathbb{R}^*\), declarar\(a\) y\(b\) estar emparentados si tienen el mismo signo. Por ejemplo,\(7.14\) y\(e\) están relacionados, así son\(-\pi\) y\(-\sqrt{2}\). Sin embargo, 5 y no lo\(-2\) son. Tenga en cuenta que\(a\) se relaciona con\(b\) implica que también\(b\) se relaciona con\(a\).

Ejemplo\(\PageIndex{2}\label{eg:defnrelat-02}\)

Para\(a,b\in\mathbb{R}\), defina “\(a\)está relacionado con\(b\)” si y solo si\(a<b\). Toma nota de eso\(3<5\), pero\(5\nless3\). Esto demuestra que\(a\) se relaciona con\(b\) no implica necesariamente que también\(b\) se relaciona con\(a\).

Ejemplo\(\PageIndex{3}\label{eg:defnrelat-03}\)

Seamos\(A\) un conjunto de alumnos, y dejemos\(B\) ser un conjunto de cursos. Dado\(a\in A\) y\(b\in B\), definir “\(a\)está relacionado con\(b\)” si y sólo si el estudiante\(a\) está tomando curso\(b\). Si bien podría ser posible que “John Smith esté relacionado con MATH 210” porque John está tomando MATH 210, ciertamente es absurdo decir que “MATH 210 está relacionado con John Smith”, porque no tiene mucho sentido decir que MATH 210 se está llevando a John Smith. Esto nuevamente ilustra que\(a\) está relacionado con\(b\) no implica necesariamente que también\(b\) esté relacionado con\(a\).

En estos ejemplos, vemos que cuando decimos “\(a\)está relacionado con”\(b\), el orden en que\(a\)\(b\) aparecen puede marcar la diferencia. Esto sugiere la siguiente definición.

Definición

Una relación de un conjunto\(A\) a un conjunto\(B\) es un subconjunto de\(A \times B\). De ahí que una relación\(R\) consiste en pares ordenados\((a,b)\), donde\(a\in A\) y\(b\in B\). Si\((a,b)\in R\), decimos que está relacionado con, y también escribimos\(a\,R\,b\).

Comentario

También podemos reemplazar\(R\) por un símbolo, especialmente cuando uno está fácilmente disponible. Esto es exactamente lo que hacemos en, por ejemplo,\(a<b\). Decir que no es cierto eso\(a<b\), podemos escribir\(a\nless b\). Del mismo modo\((a,b)\notin R\), si, entonces no\(a\) está relacionado con\(b\), y podríamos escribir\(a\!\not\!R\,b\). Pero la barra puede no ser fácil de reconocer cuando está escrita sobre una letra mayúscula. En este sentido, puede ser una buena práctica evitar usar la notación de barra sobre una letra. Alternativamente, se puede usar la notación de “barra”\(\overline{a\,R\,b}\) para indicar eso\(a\) y no\(b\) están relacionados.

Ejemplo\(\PageIndex{4}\label{eg:defnrelat-04}\)

Definir\(R=\{(a,b)\in\mathbb{R}^2 \mid a<b \}\), de ahí\((a,b)\in R\) si y sólo si\(a<b\). Obviamente, decir “\(a<b\)” es mucho más claro que “”\(a\,R\,b\). Si\(a\) y no\(b\) están relacionados, podríamos decir\((a,b)\notin R\), o\(a\nless b\).

Ejemplo\(\PageIndex{5}\label{eg:defnrelat-05}\)

Definir\[F = \left\{(x,y)\in\mathbb{R}^2 \biggm| y=\frac{1}{x^2+1} \right\}. \nonumber\] Por lo tanto\(x\) se relaciona con\(y\) si y solo si\(y=\frac{1}{x^2+1}\). También podemos escribir\[F = \left\{\left(x,\frac{1}{x^2+1}\right) \biggm| x\in\mathbb{R} \right\}, \nonumber\] lo que puede parecer un poco más sencillo.

Por ejemplo,\((1,0.5)\in F\), pero\((1,0)\not\in F\). En este caso, probablemente\((2,0.2)\in F\) sea más fácil de entender que\(2\,F\,0.2\). De igual manera,\((1,2)\notin F\) puede ser más fácil de leer que\(1\!\not\!F\,2\).

Ejercicio práctico\(\PageIndex{1}\label{he:defnrelat-01}\)

Definir la relación\(H\) como\(\{(x,x^2+1)\mid x\in\mathbb{R}\}\). Determinar si las siguientes afirmaciones\[\textstyle 2\,H\,3, \quad (-4,17)\notin H, \quad \big(\frac{1}{2},\frac{3}{2}\big)\notin H, \quad (\sqrt{2},3)\in H, \quad (1,2)\in H, \nonumber\] son verdaderas o falsas.

Ejercicio práctico\(\PageIndex{2}\label{he:defnrelat-02}\)

Vamos\(G=\{(x,y)\in\mathbb{R}^2 \mid xy=1\}\). ¿2 está relacionado con 0.5? ¿Cómo lo escribirías? Repita con 4 y 0.5, y con 10 y 3.

Ejercicio práctico\(\PageIndex{3}\label{he:defnrelat-03}\)

En el último ejemplo, ¿0 está relacionado con 3? ¿Cómo lo escribirías? Repita con 1 y\(-1\). De nuevo con\(\frac{1}{\sqrt{2}}\) y\(\sqrt{2}\).

Como una relación es un conjunto, podemos describir una relación enumerando sus elementos (es decir, usando el método roster).

Ejemplo\(\PageIndex{6}\label{eg:parity}\)

Dejar\(A=\{1,2,3,4,5,6\}\) y\(B=\{1,2,3,4\}\). Definir\((a,b)\in R\) si y solo si\((a-b)\bmod 2 = 0\). Entonces\[R=\{(1,1), (1,3), (2,2), (2,4), (3,1), (3,3), (4,2), (4,4), (5,1), (5,3), (6,2), (6,4)\}. \nonumber\] observamos que\(R\) consiste en pares ordenados\((a,b)\) donde\(a\) y\(b\) tienen la misma paridad. Sea cauteloso, eso\(1\leq a\leq 6\) y\(1\leq b\leq 4\). De ahí que no tenga sentido hablar de si\((1,5)\in R\) o\((1,5)\notin R\).

Ejercicio práctico\(\PageIndex{4}\label{he:relat-div}\)

Dejar\(A=\{2,3,4,7\}\) y\(B=\{1,2,3,\ldots,12\}\). Definir\(a\,S\,b\) si y solo si\(a\mid b\). Utilice el método de roster para describir\(S\).

En el último ejemplo, 7 nunca aparece como el primer elemento (en la primera coordenada) de ningún par ordenado. Asimismo, 1, 5, 7 y 11 nunca aparecen como el segundo elemento (en la segunda coordenada) de ningún par ordenado.

Definición

El dominio de una relación\(R\subseteq A\times B\) se define como\[\mbox{dom}\,R = \{ a\in A \mid (a,b)\in R \mbox{ for some $b\in B$} \}, \nonumber\] y la imagen o rango se define como\[\mathrm{ im }{R} = \{ b\in B \mid (a,b)\in R \mbox{ for some $a\in A$} \}. \nonumber\]

Ejercicio práctico\(\PageIndex{5}\label{he:defnrelat-05}\)

Encuentra\(\mbox{dom}\,S\) y\(\mathrm{ im }{S}\), dónde\(S\) en Ejercicio Práctico 7.1.4.

Una relación se\(R\subseteq A\times B\) puede mostrar gráficamente en un dígrafo que también se llama gráfico dirigido. Representar los elementos desde\(A\) y\(B\) por vértices o puntos, y usar líneas dirigidas (también llamadas aristas o arcos dirigidos) para conectar dos vértices si los elementos correspondientes están relacionados. La figura\(\PageIndex{1}\) muestra una representación gráfica de la relación en el Ejemplo 7.1.6.

Figura\(\PageIndex{1}\): La representación gráfica de la relación a.

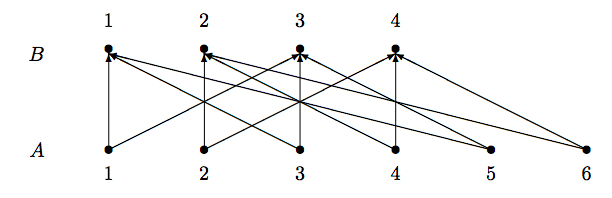
Aunque un dígrafo nos da una representación visual clara y precisa de una relación, podría llegar a ser muy confuso y difícil de leer cuando la relación contiene muchos pares ordenados. Como veremos en la Sección 4, a veces podemos simplificar los dígrafos en algunas situaciones especiales. De lo contrario, la representación gráfica sólo es efectiva para las relaciones con un pequeño número de pares ordenados.

Podemos usar una representación matricial para describir una relación. Una matriz consiste en valores dispuestos en filas y columnas. Una relación\(R\) de\(A=\{a_1,\ldots, a_m\}\) a\(B=\{b_1,\ldots,b_n\}\) puede ser descrita por una\(n\) matriz\(m\) -by-\(M=(m_{ij})\) cuya entrada en fila\(i\) y columna\(j\) está definida por\[m_{ij} = \cases{ 1 & if $a_i\,R\,b_j$, \cr 0 & otherwise. \cr} \nonumber\] La matriz\(M\) se denomina matriz de incidencia para\(R\).

Ejemplo\(\PageIndex{7}\label{eg:defnrelat-07}\)

La matriz de incidencia para la relación\(R\) en el Ejemplo 7.1.6 es\[\begin{array}{cc} & \begin{array}{cccc} 1 & 2 & 3 & 4 \end{array} \\ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ 5 \\ 6 \end{array} & \left(\begin{array}{cccc} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \end{array}\right) \end{array} \nonumber\] en la que etiquetamos las filas y columnas con los elementos involucrados en la relación.

Ejercicio práctico\(\PageIndex{6}\label{he:defnrelat-06}\)

Determinar la matriz de incidencia para la relación\(S\) en el Ejercicio Práctico 7.1.4.

Ejercicio práctico\(\PageIndex{7}\label{he:defnrelat-07}\)

Los cursos tomados por John, Mary, Paul y Sally se enumeran a continuación.

Juan:	MATEMÁTICAS 210, CSIT 121, MATEMÁTICAS 223
María:	MATEMÁTICAS 231, CSIT 121, MATEMÁTICAS 210
Pablo:	CSIT 120, MATEMÁTICAS 231, MATEMÁTICAS 223
Sally:	MATEMÁTICAS 210, CSIT 120

Representar, utilizando una gráfica y una matriz, la relación\(R\) definida como\(a\,R\,b\) si el alumno\(a\) estuviera tomando curso\(b\).

Resumen y revisión

• Las relaciones son generalizaciones de funciones. Una relación se limita a afirmar que los elementos de dos conjuntos\(A\) y\(B\) están relacionados de cierta manera.
• De manera más formal, una relación se define como un subconjunto de\(A\times B\).
• El dominio de una relación es el conjunto de elementos en\(A\) que aparecen en las primeras coordenadas de algunos pares ordenados, y la imagen o rango es el conjunto de elementos en\(B\) que aparecen en las segundas coordenadas de algunos pares ordenados.
• Por brevedad y claridad, a menudo escribimos\(x\,R\,y\) si\((x,y)\in R\).
• Bajo esta convención, las notaciones matemáticas\(\leq\),\(\geq\),\(=\),\(\subseteq\), y sus similares, pueden ser consideradas como operadores relacionales.

Ejercicio\(\PageIndex{1}\label{ex:defnrelat-01}\)

Representar cada una de las siguientes relaciones desde\(\{1,2,3,6\}\) hasta\(\{1,2,3,6\}\) usando un dígrafo y una matriz de incidencia.

1. \(\{(x,y)\mid x = y\}\)
2. \(\{(x,y)\mid x\neq y\}\)
3. \(\{(x,y)\mid x < y\}\)

Ejercicio\(\PageIndex{2}\label{ex:defnrelat-02}\)

Encuentra el dominio y la imagen de cada relación en Problema 7.1.1.

Ejercicio\(\PageIndex{3}\label{ex:defnrelat-03}\)

Representar cada una de las siguientes relaciones desde\(\{1,2,3,6\}\) hasta\(\{1,2,3,6\}\) usando un dígrafo y una matriz de incidencia.

1. \(\{(x,y)\mid x^2\leq y\}\)
2. \(\{(x,y) \mid x \)divide\(y \}\)
3. \(\{(x,y) \mid x + y\)es parejo\(\}\)

Ejercicio\(\PageIndex{4}\label{ex:defnrelat-04}\)

Encuentra el dominio y la imagen de cada relación en Problema 7.1.3.

Ejercicio\(\PageIndex{5}\label{ex:defnrelat-05}\)

Encuentra la matriz de incidencia para cada una de las siguientes relaciones de\(\{1,2,3,4\}\) a\(\{1,2,3,4,5\}\).

1. \(R=\{(1,1),(2,2),(2,3),(3,3),(3,4),(4,5)\}\)
2. \(S=\{(1,1),(1,2),(2,2),(2,3),(3,3),(3,4),(4,4)\}\)
3. \(T=\{(1,5),(2,4),(3,3),(4,1),(4,4)\}\)

Ejercicio\(\PageIndex{6}\label{ex:defnrelat-06}\)

Determinar la matriz de incidencia y el dígrafo que representan la relación\(R\) definida\(\{x\in\mathbb{Z} \mid -3\leq x\leq3\}\) por\[x\,R\,y \Leftrightarrow 3\mid(x-y). \nonumber\]

Ejercicio\(\PageIndex{7}\label{ex:defnrelat-07}\)

Determinar la matriz de incidencia y el dígrafo que representan la relación\(S\) definida\(\{1,2,4,5,10,20\}\) por\[x\,S\,y \Leftrightarrow \mbox{($x<y$ and $x$ divides $y$)}. \nonumber\]

Ejercicio\(\PageIndex{8}\label{ex:defnrelat-08}\)

\(D=\{1,2,3,\ldots,30\}\)Sea el conjunto de fechas en noviembre, y que el\(W=\{\) domingo, lunes, martes, miércoles, jueves, viernes, sábado\(\}\) sea el conjunto de días de la semana. Para noviembre de este año, definir la relación\(T\) de\(D\) a\(W\) por\[(x,y)\in T \Leftrightarrow \mbox{$x$ falls on $y$}. \nonumber\] Listar los pares ordenados en\(T\). Es\(T\) una función de\(T\) a\(W\)?

Ejercicio\(\PageIndex{9}\label{ex:defnrelat-09}\)

Encuentra la matriz de incidencia para la relación\(I\subseteq \wp(\{1,2\}) \times \wp(\{1,2\})\), donde\[(S,T)\in I \Leftrightarrow S\cap T\neq\emptyset. \nonumber\]

Ejercicio\(\PageIndex{10}\label{ex:defnrelat-10}\)

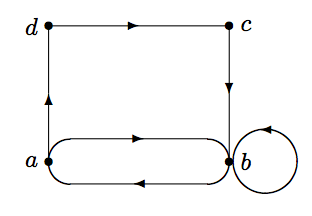
Para una relación\(R\subseteq A\times A\), en lugar de usar dos filas de vértices en un dígrafo, podemos usar un dígrafo en los vértices que representan los elementos de\(A\). De ahí que sea posible tener dos arcos dirigidos entre un par de vértices, y un bucle puede aparecer alrededor de un vértice\(x\) if\((x,x)\in R\). Encuentre la matriz de incidencia para la relación representada por el siguiente dígrafo: