4.2: Medidas de probabilidad

Bien, hemos definido espacios de muestra y eventos, pero ¿cuándo entran en juego nociones cuantitativas como “las probabilidades de” y el “porcentaje de probabilidad”? Entran en escena cuando definimos una medida de probabilidad. Una medida de probabilidad es simplemente una función desde el dominio de eventos hasta el codominio de números reales. Normalmente usaremos las letras “Pr” para nuestra medida de probabilidad. En símbolos,\(\text{Pr}:\mathbb{P}(\Omega) \to \mathbb{R}\) (ya que el conjunto de todos los eventos es el conjunto de potencia del espacio de muestreo, como se indicó anteriormente). Sin embargo, en realidad hay otra restricción que es que los valores de Pr deben estar en el rango de 0 a 1, inclusive. Entonces es más correcto escribir:\(\text{Pr}:\mathbb{P}(\Omega)\to [0,1]\). (Puede recordar de un curso anterior de matemáticas que '[' y ']' se utilizan para describir un intervalo cerrado en el que los puntos finales se incluyen en el intervalo).

El “significado” de la medida de probabilidad es lo suficientemente intuitivo: indica la probabilidad de que pensemos que ocurra cada evento. En el ejemplo del bebé, si decimos Pr ({niño}) = .5, significa que hay una probabilidad .5 (a.k.a., una probabilidad del 50%) de que nazca un hijo varón. En el ejemplo del juego, si decimos Pr (\(M\)) = .667, si significa que hay dos tercios de posibilidades de que gane el derecho de ir primero. En todos los casos, una probabilidad de 0 significa “imposible de ocurrir” y una probabilidad de 1 significa “absolutamente seguro de que ocurra”. En el inglés coloquial, la mayoría de las veces usamos porcentajes para hablar de estas cosas: diremos “hay un 60% de posibilidades de que Obama gane las elecciones” en lugar de “hay una probabilidad de .6 de que Obama gane”. Sin embargo, las matemáticas son un poco más torpes si tratamos con porcentajes, así que a partir de ahora vamos a tener el hábito de usar probabilidades en lugar de 'posibilidades porcentajes', y usaremos valores en el rango de 0 a 1 en lugar de 0 a 100.

Encuentro que la manera más fácil de pensar sobre las medidas de probabilidad es comenzar con las probabilidades de los resultados, no por los eventos. Cada resultado tiene una probabilidad específica de ocurrir. Las probabilidades de eventos fluyen lógicamente de eso con solo usar la suma, como veremos en un momento.

Por ejemplo, imaginemos que Fox Broadcasting está produciendo un evento televisivo mundial llamado All-time Idol, en el que los ganadores anuales de American Idol a lo largo de su historia compiten entre sí para ser coronados como el “campeón de todos los tiempos de American Idol”. Los cuatro concursantes elegidos para esta competencia, junto con sus géneros musicales, y la edad al aparecer originalmente en el programa, son los siguientes:

Kelly Clarkson (20): pop, rock, R&B
Fantasia Barrino (20): pop, R&B
Carrie Underwood (22): país
David Cook (26): rock

Los espectáculos de entretenimiento, las columnas de chismes y la revista People están todos alborotados en las semanas anteriores a la competencia, hasta el punto en que un analista astuto puede estimar las probabilidades de que cada concursante gane. Nuestras mejores estimaciones actuales son: Kelly .2, Fantasia .2, Carrie .1 y David .5.

Calcular la probabilidad de un evento específico es solo cuestión de sumar las probabilidades de sus resultados. Definir\(F\) como el evento que una mujer gana la competencia. Claramente Pr (\(F\)) = .5, ya que Pr ({Kelly}) = .2, Pr ({Fantasia}) = .2, y Pr ({Carrie}) = .1. Si\(P\) es el evento que gana un cantante de rock, Pr (\(P\)) = .7, ya que esta es la suma de las probabilidades de Kelly y David.

Ahora resulta que no cualquier función hará como medida de probabilidad, incluso si el dominio (eventos) y el codominio (números reales en el rango [0,1]) son correctos. Para que una función sea una medida de probabilidad “válida”, debe cumplir varias otras reglas:

1. [algo pasa]\(\text{Pr}(\Omega) = 1\)

2. [nonegs]\(\text{Pr}(A) \geq 0\) para todos\(A \subseteq \Omega\)

3. [probunion]\(\text{Pr}(A \cup B) = \text{Pr}(A) + \text{Pr}(B) - \text{Pr}(A \cap B)\)

Regla 1 básicamente significa “algo tiene que suceder”. Si creamos un evento que incluya todos los resultados posibles, entonces hay una probabilidad de 1 (100% de probabilidad) de que ocurra el evento, porque después de todo tiene que ocurrir algún resultado. (Y claro que Pr (\(\Omega\)) tampoco puede ser mayor que 1, porque no tiene sentido tener ninguna probabilidad superior a 1.) La regla 2 dice que no hay probabilidades negativas: no se puede definir ningún evento, por remoto que sea, que tenga menos de cero posibilidades de suceder.

La regla 3 se llama la “propiedad de aditividad”, y es un poco más difícil de entender. Un diagrama hace maravillas. Considere Figura [venn], llamada “diagrama de Venn”, que representa visualmente conjuntos y su contenido. Aquí hemos definido tres eventos:\(F\) (como arriba) es el evento de que el ganador es una mujer;\(R\) es el evento de que el ganador es un músico de rock (quizás además de otros géneros musicales); y\(U\) es el evento de que el ganador es menor de edad (i.e. , se convierte en un multimillonario antes de que puedan beber legalmente). Cada uno de estos eventos se representa como una curva cerrada que encierra los resultados que le pertenecen. Obviamente hay mucho solapamiento.

Ahora volvamos a la regla 3. Supongamos que pregunto “¿cuál es la probabilidad de que el ganador de todos los tiempos Idol sea menor de edad o una estrella de rock?” Enseguida nos enfrentamos a una ambigüedad irritante en el idioma inglés: ¿“o” significa “menor de edad o una estrella de rock, pero no ambos?” ¿O significa “menor de edad y/o estrella de rock?” A la primera interpretación se le llama exclusiva o y la segunda una inclusiva o. En informática, casi siempre estaremos asumiendo un inclusivo o, a menos que se indique explícitamente lo contrario.

Figura\(\PageIndex{1}\): Diversos eventos, y su superposición.

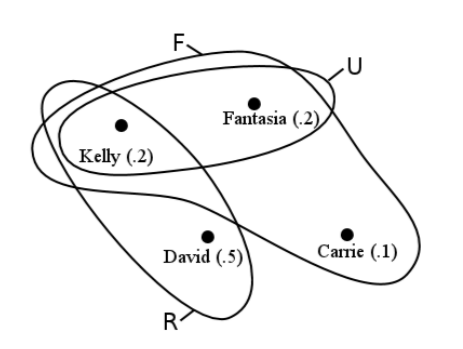
Muy bien entonces. Lo que realmente estamos preguntando aquí es “¿qué es Pr (\(U \cup R\))?” Queremos la unión de los dos eventos, ya que estamos pidiendo la probabilidad de que se produzca alguno (o ambos) de ellos. Primero podrías pensar que agregaríamos las dos probabilidades para los dos eventos y terminaríamos con ello, pero un vistazo al diagrama te dice que esto significa problemas. Pr (\(U\)) es .4, y Pr (\(R\)) es .7. Aunque no fuéramos muy inteligentes, sabríamos que algo andaba mal tan pronto como agregáramos\(.4 + .7 = 1.1\) para obtener una probabilidad de más de 1 y violar la regla 1. Pero somos inteligentes, y mirando el diagrama es fácil ver qué pasó: contamos dos veces la probabilidad de Kelly. Kelly era miembro de ambos grupos, por lo que su .2 fue contada ahí dos veces. Ahora se puede ver la justificación de la regla 3. Para obtener Pr (\(U \cup R\)) sumamos Pr (\(U\)) y Pr (\(R\)), pero luego tenemos que restar la parte que doblemente contamos. ¿Y qué contábamos dos veces? Precisamente la intersección\(U \cap R\).

Como segundo ejemplo, ¿supongamos que queremos la probabilidad de un menor de edad o de una mujer ganadora? Pr (\(U\)) = .4, y Pr (\(F\)) = .5, así que el primer paso es simplemente agregar estos. Después restamos la intersección, la cual doble contabilizamos. En este caso, la intersección\(U \cap F\) es justa\(U\) (revisa el diagrama), y así restar todo el .4. La respuesta es .5, como debería ser.

Por cierto, notarás que si los dos conjuntos en cuestión son mutuamente excluyentes, entonces no hay intersección para restar. Ese es un caso especial de la regla 3. Por ejemplo, supongamos que definí el evento\(C\) como un cantante de country ganando la competencia. En este caso,\(C\) contiene sólo un desenlace: Carrie. Por lo tanto\(U\) y\(C\) son mutuamente excluyentes. Entonces, si le pregunto “¿cuál es la probabilidad de que un menor de edad o un país sea ganador?” calcularíamos Pr (\(U \cup C\)) como

\[\begin{aligned} \text{Pr}(U \cup C) &= \text{Pr}(U) + \text{Pr}(C) - \text{Pr}(U \cap C) \\ &= .4 + .1 - 0 \\ &= .5.\end{aligned}\]

No contábamos nada doble, así que no había ninguna corrección que hacer.

Aquí hay algunas reglas más bastante obvias para las medidas de probabilidad, que siguen lógicamente desde los primeros 3:

4. Pr (\(\varnothing\)) = 0

5. Pr (\(\overline{A}\)) =\(1-\) Pr (\(A\)) (recordar el operador “complemento total” de p.)

6. Pr (\(A\))\(\leq\) Pr (\(B\)) si\(A \subseteq B\)

Por último, permítaseme llamar la atención sobre un caso especial común de las reglas anteriores, que es la situación en la que todos los resultados son igualmente probables. Esto suele suceder cuando tiramos dados, volteamos monedas, repartimos cartas, etc. ya que la probabilidad de rodar un 3 es (normalmente) la misma que rodar un 6, y la probabilidad de que se repartan el 10\(\spadesuit\) es la misma que la Q\(\diamondsuit\). También puede suceder cuando generamos claves de cifrado, elegimos entre rutas de enrutamiento de red alternativas o determinamos las posiciones iniciales de los malos en un nivel de disparos en primera persona.

En este caso, si hay\(N\) posibles resultados (nota\(N=|\Omega|\)) entonces la probabilidad de cualquier evento A es:

Pr (\(A\)) =\(\dfrac{|A|}{N}\).

Lo que importa es el tamaño (cardinalidad) del conjunto de eventos, y la relación entre este número y el número total de eventos es la probabilidad. Por ejemplo, si repartimos una carta de una baraja justa, la probabilidad de sacar una carta facial es

\[\begin{aligned} \text{Pr}(F) &= \frac{|F|}{N} \\[.1in] &= \frac{|\{K\spadesuit,K\heartsuit,K\diamondsuit,\cdots,J\clubsuit\}|}{52} \\[.1in] &= \frac{12}{52} = .231.\end{aligned}\]

Por favor, tenga en cuenta que este atajo solo se aplica cuando la probabilidad de cada resultado es la misma. Ciertamente no podríamos decir, por ejemplo, que la probabilidad de que la contraseña de un usuario empiece por la letra q sea justa\(\frac{1}{26}\), porque las contraseñas seguramente no contienen todas las letras con igual frecuencia. (Al menos, me sorprendería mucho si ese fuera el caso). La única manera de resolver un problema como este es saber con qué frecuencia ocurre cada letra del alfabeto.