5.1: Gráficas

En muchos sentidos, la forma más elegante, sencilla y poderosa de representar el conocimiento es por medio de una gráfica. Una gráfica está compuesta por un montón de pequeños bits de datos, cada uno de los cuales puede (o no) estar unido a cada uno de los otros. Un ejemplo está en la Figura\(\PageIndex{1}\). Cada uno de los óvalos etiquetados se llama vértice (plural: vértices), y las líneas entre ellos se llaman bordes. Cada vértice contiene, o no, un borde que lo conecta entre sí. Uno podría imaginarse que cada uno de los vértices contiene varios atributos descriptivos —quizás el óvalo de John Wilkes Booth tendría información sobre la fecha de nacimiento de Booth y la información de Washington, DC sobre su longitud, latitud y población— pero estos generalmente no se muestran en el diagrama. Todo lo que realmente importa, en cuanto a gráficos, es qué vértices contiene, y cuáles están unidos a qué otros.

Figura\(\PageIndex{1}\): Una gráfica (no dirigida).

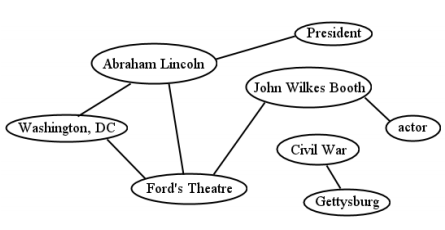
Los psicólogos cognitivos, que estudian los procesos mentales internos de la mente, han identificado desde hace mucho tiempo este tipo de estructura como la principal forma en que las personas almacenan mentalmente y trabajan con la información. Después de todo, si retrocedes un momento y preguntas “¿cuáles son las 'cosas' que hay en mi memoria?” una respuesta razonable es “bueno, sé sobre un montón de cosas, y las propiedades de esas cosas, y las relaciones entre esas cosas”. Si las “cosas” son vértices, y las “propiedades” son atributos de esos vértices, y las “relaciones” son los bordes, tenemos precisamente la estructura de una gráfica. Los psicólogos le han dado otro nombre: una red semántica. Se piensa que la miríada de conceptos que has comprometido con la memoria —Abraham Lincoln, y la barra de jabón, y mi horario de otoño, y quizás millones de otros— están todos asociados en tu mente en una vasta red semántica que une los conceptos relacionados entre sí. Cuando tu mente recuerda información, o deduce hechos, o incluso deriva aleatoriamente en momentos de inactividad, esencialmente está atravesando esta gráfica a lo largo de los diversos bordes que existen entre los vértices.

Eso es profundo. Pero no hay que acercarse a esa profundidad para ver la apariencia de las estructuras gráficas en toda la informática. ¿Qué es MapQuest, si no es un gráfico gigante donde los vértices son ubicaciones transitables y los bordes son rutas entre ellos? ¿Qué es Facebook, si no es una gráfica gigante donde los vértices son personas y los bordes son amistades? ¿Qué es la World Wide Web, si no un gráfico gigante donde los vértices son páginas y los bordes son hipervínculos? ¿Qué es Internet, si no es un gráfico gigante donde los vértices son computadoras o enrutadores y los bordes son enlaces de comunicación entre ellos? Este sencillo esquema de vértices enlazados es lo suficientemente potente como para dar cabida a toda una serie de aplicaciones, por lo que merece la pena estudiarlo.

Términos de la gráfica

El estudio de las gráficas trae consigo todo un grupo de nuevos términos que son importantes para usar con precisión:

vértice. Cada gráfica contiene cero o más vértices. ¹ (A estos también se les llama a veces nodos, conceptos u objetos).

borde. Cada gráfica contiene cero o más bordes. (A estos también se les llama a veces enlaces, conexiones, asociaciones o relaciones). Cada borde conecta exactamente dos vértices, a menos que el borde conecte un vértice consigo mismo, lo cual es posible, lo creas o no. Un borde que conecta un vértice consigo mismo se llama bucle.

camino. Un camino es una secuencia de aristas consecutivas que te lleva de un vértice a otro. En Figura\(\PageIndex{1}\), hay un camino entre Washington, DC y John Wilkes Booth (por medio del Teatro Ford) a pesar de que no hay borde directo entre los dos. Por el contrario, no existe camino entre el Presidente y la Guerra Civil. No confundas los dos términos edge y path: el primero es un enlace único entre dos nodos, mientras que el segundo puede ser un recorrido completo paso a paso. (Sin embargo, un solo borde cuenta como una ruta).

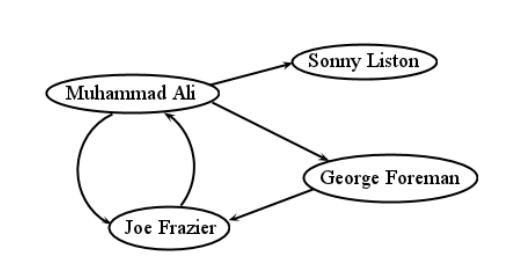
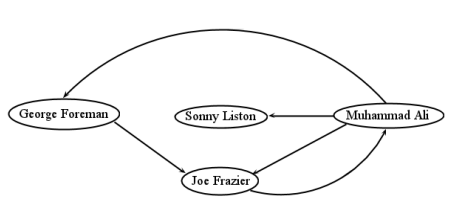
directo/no dirigido. En algunas gráficas, las relaciones entre nodos son inherentemente bidireccionales: si\(A\) está vinculado a\(B\), entonces\(B\) está vinculado a\(A\), y no tiene sentido de otra manera. Piensa en Facebook: la amistad siempre va en ambos sentidos. Este tipo de gráfica se llama gráfica no dirigida, y al igual que el ejemplo de Abraham Lincoln en la Figura\(\PageIndex{1}\), los bordes se muestran como líneas rectas. En otras situaciones, un borde de\(A\) a\(B\) no necesariamente implica uno en la dirección inversa también. En la World Wide Web, por ejemplo, el hecho de que la página web\(A\) tenga un enlace a la página web\(B\) no significa que lo contrario sea cierto (generalmente no lo es). En este tipo de gráfica dirigida, dibujamos puntas de flecha en las líneas para indicar en qué dirección va el enlace. Un ejemplo es Figura\(\PageIndex{2}\): los vértices representan boxeadores famosos, y los bordes dirigidos indican qué boxeador derrotó a qué otro (s). Es posible que un par de vértices tengan aristas en ambas direcciones —Muhammad Ali y Joe Frazier derrotaron cada uno al otro (en combates separados, claro) — pero esta no es la norma, y desde luego no la regla, con una gráfica dirigida.

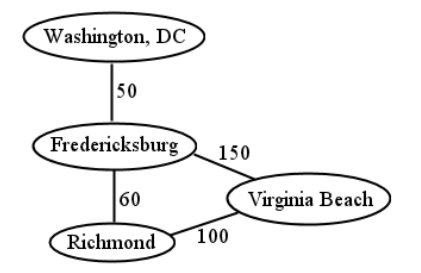
ponderado. Algunas gráficas, además de contener meramente la presencia (o ausencia) de un borde entre cada par de vértices, también tienen un número en cada borde, llamado peso del borde. Dependiendo de la gráfica, ésta puede indicar la distancia, o costo, entre vértices. Un ejemplo está en la Figura\(\PageIndex{3}\): en la verdadera manera de MapQuest, esta gráfica contiene ubicaciones, y el kilometraje entre ellas. Un gráfico puede ser tanto dirigido como ponderado, por cierto. Si un par de vértices en dicha gráfica se une “en ambos sentidos”, entonces cada uno de los dos bordes tendrá su propio peso.

Figura\(\PageIndex{2}\): Una gráfica dirigida.

Figura\(\PageIndex{3}\): Gráfica ponderada (y no dirigida).

adyacente. Si dos vértices tienen un borde entre ellos, se dice que son adyacentes.

conectado. La palabra conectada tiene dos significados: se aplica tanto a pares de vértices como a gráficas completas.

Decimos que dos vértices están conectados si hay al menos un camino entre ellos. Por lo tanto, cada vértice es “alcanzable” desde el otro. En Figura\(\PageIndex{1}\), Presidente y actor están conectados, pero el Teatro de Ford y la Guerra Civil no lo están.

“Conectado” también se utiliza para describir gráficas completas, si se puede llegar a cada nodo desde todos los demás. Es fácil ver que Figura\(\PageIndex{3}\) es un gráfico conectado, mientras que Figura no lo\(\PageIndex{1}\) es (porque Guerra Civil y Gettysburg están aislados de los otros nodos). No siempre es trivial determinar si una gráfica está conectada, sin embargo: imagínese un pantano enredado de un millón de vértices, con diez millones de aristas, y tener que averiguar si cada vértice es alcanzable o no desde todos los demás. (Y si eso parece poco realista grande, considere Facebook, que tiene más de mil millones de nodos).

grado. El grado de un vértice es simplemente el número de aristas que se conectan a él. Virginia Beach tiene grado 2, y Fredericksburg 3. En el caso de una gráfica dirigida, a veces distinguimos entre el número de flechas entrantes que tiene un vértice (llamado su grado de entrada) y el número de flechas salientes (el grado de salida). Muhammad Ali tuvo un grado superior (3) que en grado (1) ya que ganó la mayor parte del tiempo.

ciclo. Un ciclo es un camino que comienza y termina en el mismo vértice. ² En Figura\(\PageIndex{3}\), Richmond —a— Virginia Beach —a— Fredericksburg —a— Richmond es un ciclo. Cualquier bucle es un ciclo por sí mismo. Para las gráficas dirigidas, todo el bucle debe comprender bordes en la dirección “hacia adelante”: no es justo ir hacia atrás. En Figura\(\PageIndex{2}\), Frazier —a— Ali —a— Capataz —a— Frazier es un ciclo, como lo es el Ali más simple —a— Frazier —a— Ali.

DAG (gráfica dirigida, acíclica). Un uso común de las gráficas es representar flujos de dependencias, por ejemplo los requisitos previos que los diferentes cursos universitarios tienen entre sí. Otro ejemplo son los flujos de trabajo de gestión de proyectos: las tareas necesarias para completar un proyecto se convierten en vértices, y luego las dependencias que tienen entre sí se convierten en bordes. La gráfica de la Figura\(\PageIndex{4}\) muestra los pasos para hacer un lote de brownies, y cómo estos pasos dependen unos de otros. Los huevos tienen que ser agrietados antes de que los ingredientes se puedan mezclar, y el horno tiene que ser precalentado antes de hornear, pero la sartén se puede engrasar en cualquier época antigua, siempre que se haga antes de verter la goop marrón en ella.

Figura\(\PageIndex{4}\): Un DAG.

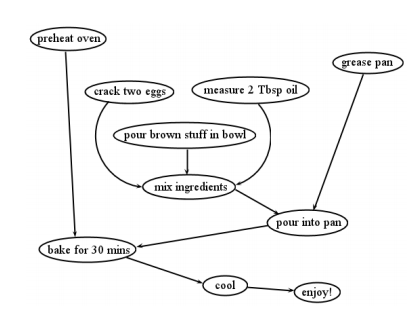
Una gráfica de dependencias como esta debe ser tanto dirigida como acíclica, o no tendría sentido. Dirigido, por supuesto, significa que la tarea X puede requerir que la tarea Y se complete antes que ésta, sin que lo contrario también sea cierto. Si ambos dependieran el uno del otro, tendríamos un bucle infinito, ¡y ningún brownies podría hornearse nunca! Acíclico significa que no puede existir ningún tipo de ciclo en la gráfica, incluso uno que atraviesa múltiples vértices. Tal ciclo volvería a resultar en un bucle infinito, haciendo que el proyecto fuera de esperanza. Imagínese si hubiera una flecha de hornear durante 30 minutos de regreso a la bandeja de engrase en la Figura\(\PageIndex{4}\). Entonces, tendríamos que engrasar la sartén antes de verterla en ella, y tendríamos que verter la goop antes de hornear, ¡pero también tendríamos que hornear antes de engrasar la sartén! Estaríamos atrapados de inmediato: no habría forma de completar ninguna de esas tareas ya que todas dependerían indirectamente el uno del otro. Una gráfica que es tanto dirigida como acíclica (y por lo tanto libre de estos problemas) a veces se llama DAG para abreviar.

Posicionamiento espacial

Una cosa importante a entender acerca de las gráficas es qué aspectos de un diagrama son relevantes. Específicamente, el posicionamiento espacial de los vértices no importa. En Figura\(\PageIndex{2}\) dibujamos a Muhammad Ali en la mitad superior izquierda, y Sonny Liston en la parte superior derecha extrema. Pero esta fue una elección arbitraria, e irrelevante. Más específicamente, esto no es parte de la información que el diagrama afirma representar. Podríamos haber posicionado los vértices de manera diferente, como en la Figura\(\PageIndex{5}\), y tener la misma gráfica. En ambos diagramas, hay los mismos vértices, y los mismos bordes entre ellos (verifícame). Por lo tanto, estas son matemáticamente la misma gráfica.

Figura\(\PageIndex{5}\): Una mirada diferente a la misma gráfica que la Figura\(\PageIndex{2}\).

Esto puede no parecer sorprendente para el gráfico de luchadores premiados, pero para gráficos como el gráfico de MapQuest, que en realidad representan ubicaciones físicas, puede parecer discordante. En Figura\(\PageIndex{3}\) podríamos haber dibujado Richmond al norte de Fredericksburg, y Virginia Beach en el extremo oeste del diagrama, y todavía tenía la misma gráfica, siempre que todos los nodos y enlaces fueran iguales. Solo recuerda que el posicionamiento espacial está diseñado para la comodidad humana, y no forma parte de la información matemática. Es similar a como no hay orden para los elementos de un conjunto, aunque cuando especificamos un conjunto extensivamente, tenemos que enumerarlos en algún orden para evitar escribir todos los nombres de los elementos uno encima del otro. En un diagrama gráfico, tenemos que dibujar cada vértice en alguna parte, pero donde lo ponemos es simplemente estético.

Parece que nos hemos desviado muy lejos de los sets con todas estas cosas gráficas. Pero en realidad, hay algunas conexiones importantes que hay que hacer con esos conceptos originales. Recordemos el conjunto\(A\) de magos del capítulo que extendimos para contener {Harry, Ron, Hermione, Neville}. Consideremos ahora la siguiente endorelación sobre\(A\):

(Harry, Ron)
(Ron, Harry)
(Ron, Hermione)
(Ron, Neville)
(Hermione, Hermione)
(Neville, Harry)

Esta relación, y todo lo que contiene, está representada fielmente por la gráfica de la Figura\(\PageIndex{6}\). Los elementos de\(A\) son los vértices por supuesto, y cada par ordenado de la relación se refleja en un borde de la gráfica. ¿Puedes ver cómo exactamente la misma información está representada por ambas formas?

Figura\(\PageIndex{6}\): Gráfica que representa una endorelación.

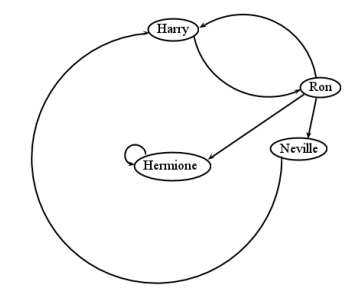
La figura\(\PageIndex{6}\) es una gráfica dirigida, por supuesto. ¿Y si se tratara de una gráfica no dirigida? La respuesta es que la relación correspondiente sería simétrica. Una gráfica no dirigida implica que si hay un borde entre dos vértices, va “en ambos sentidos”. Esto es realmente idéntico a decir que una relación es simétrica: si an\((x,y)\) está en la relación, entonces la correspondiente también\((y,x)\) debe serlo. Un ejemplo es la Figura\(\PageIndex{7}\), que representa la siguiente relación simétrica:

(Harry, Ron)
(Ron, Harry)
(Ron, Hermione)
(Hermione, Ron)
(Harry, Harry)
(Neville, Neville)

Figura\(\PageIndex{7}\): Gráfica que representa una endorelación simétrica.

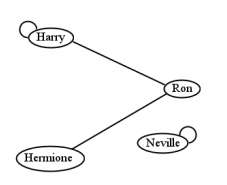
Observe cómo los bucles (bordes de un nodo de vuelta a sí mismo) en estos diagramas representan pares ordenados en los que ambos elementos son iguales.

Otra conexión entre gráficas y conjuntos tiene que ver con particiones. La figura no\(\PageIndex{7}\) era una gráfica conectada: No se pudo llegar a Neville desde ninguno de los otros nodos. Ahora considere: ¿no es una gráfica como esta similar en cierto modo a una partición de\(A\) — es decir, ésta?

{Harry, Ron, Hermione} y {Neville}.

Simplemente hemos particionado los elementos de\(A\) en los grupos que están conectados. Si eliminas el borde entre Harry y Ron en esa gráfica, tienes:

{Harry}, {Ron, Hermione}, y {Neville}.

Luego agrega uno entre Hermione y Neville, y ahora tienes:

{Harry} y {Ron, Hermione, Neville}.

En otras palabras, la “conectividad” de una gráfica se puede representar precisamente como una partición del conjunto de vértices. Cada subconjunto conectado está en su propio grupo, y cada vértice está en un solo grupo: por lo tanto, estos grupos aislados son mutuamente excluyentes y colectivamente exhaustivos. Fresco.

Trayectoria gráfica

Si tuvieras una larga lista —tal vez de números de teléfono, nombres o órdenes de compra— y necesitabas pasar y hacer algo a cada elemento de la lista, marcar todos los números, escanear la lista para un nombre determinado, sumar todos los pedidos, sería bastante obvio cómo hacerlo. Simplemente comienzas por la parte superior y trabajas tu camino hacia abajo. Puede ser tedioso, pero no es confuso.

Iterar a través de los elementos como este se llama atravesar la estructura de datos. Quieres asegurarte de encontrar cada elemento una vez (y solo una vez) para que puedas hacer lo que sea necesario hacer con él. Está claro cómo recorrer una lista. Pero, ¿cómo atravesar una gráfica? No hay un “primer” o “último” nodo obvio, y cada uno está vinculado a potencialmente muchos otros. Y como hemos visto, es posible que los vértices ni siquiera estén completamente conectados, por lo que una ruta de recorrido a través de todos los nodos puede que ni siquiera exista.

Hay dos formas diferentes de atravesar una gráfica: primero en ancho y primero en profundidad. Proporcionan diferentes formas de explorar los nodos, y como efecto secundario, cada uno es capaz de descubrir si la gráfica está conectada o no. Veamos cada uno a su vez.

Primer recorrido de la anchura

Con el recorrido de primer ancho, comenzamos en un vértice inicial (no importa cuál) y exploramos la gráfica con cautela y delicadeza. Sondeamos igualmente profundo en todas las direcciones, asegurándonos de haber buscado un poco hacia abajo en cada camino posible antes de explorar cada uno de esos caminos un poco más lejos.

Para ello, utilizamos una estructura de datos muy simple llamada cola. Una cola es simplemente una lista de nodos que están esperando en la fila. (En Gran Bretaña, me dicen, en lugar de decir “alinearse” en la tienda de sándwiches, dicen “hacer cola”). Cuando ingresamos a un nodo en la cola en el extremo de cola, lo llamamos enqueueing el nodo, y cuando eliminamos uno del frente, lo llamamos deshacer la cola del nodo. Los nodos en el medio esperan pacientemente su turno para ser tratados, acercándose al frente cada vez que se deja de cola al nodo frontal.

Un ejemplo de esta estructura de datos en acción se muestra en la Tabla\(\PageIndex{1}\). Tenga en cuenta cuidadosamente que siempre insertamos nodos en un extremo (a la derecha) y los retiramos del otro extremo (el izquierdo). Esto significa que el primer elemento a poner en cola (en este caso, el triángulo) será el primero en ser descolado. “Las llamadas serán atendidas en el orden en que fueron recibidas”. Este hecho ha dado lugar a otro nombre para una cola: un “FIFO”, que significa “primero en entrar, primero en salir”.

Tabla\(\PageIndex{1}\): Una cola en acción. La barra vertical marca el “frente de la línea”, y los elementos están a la espera de ser dejados de cola en orden de izquierda a derecha.

Comience con una cola vacía:	\(|\)
Poner en cola un triángulo, y tenemos:	\(|\triangle\)
Poner en cola una estrella, y tenemos:	\(|\triangle \bigstar\)
Poner en cola un corazón, y tenemos:	\(|\triangle \bigstar \heartsuit\)
Quita la cola del triángulo, y tenemos:	\(|\bigstar \heartsuit\)
Poner en cola un club, y tenemos:	\(|\bigstar \heartsuit \clubsuit\)
Quita la cola a la estrella, y tenemos:	\(|\heartsuit \clubsuit\)
Quita la cola del corazón, y tenemos:	\(|\clubsuit\)
Quita la cola al club. Estamos vacíos otra vez:	\(|\)

Ahora bien, así es como usamos una cola para recorrer primero una gráfica en profundidad. Vamos a comenzar en un nodo en particular, y poner todos sus nodos adyacentes en una cola. Esto hace que todos ellos “esperen en la fila” de manera segura hasta que lleguemos a explorarlos. Entonces, tomamos repetidamente el primer nodo en línea, hacemos lo que sea necesario que hagamos con él, y luego ponemos todos sus nodos adyacentes en línea. Seguimos haciendo esto hasta que la cola esté vacía.

Ahora se te podría haber ocurrido que podemos encontrarnos con problemas si nos encontramos con el mismo nodo varias veces mientras estamos atravesando. Esto puede suceder si la gráfica tiene un ciclo: habrá más de una ruta para llegar a algunos nodos, y podríamos quedarnos atascados en un bucle infinito si no tenemos cuidado. Por esta razón, introducimos el concepto de marcar nodos. Esto es como dejar un rastro de migas de pan: si alguna vez estamos a punto de explorar un nodo, pero nos enteramos de que está marcado, entonces sabemos que ya hemos estado ahí, y no tiene sentido volver a buscarlo.

Así que hay dos cosas que vamos a hacer a los nodos a medida que busquemos:

• Marcar un nodo significa recordar que ya lo hemos encontrado en el proceso de nuestra búsqueda.

• Visitar un nodo significa realmente hacer lo que sea que tengamos que hacer al nodo (llamar al número de teléfono, examinar su nombre para una coincidencia de patrón, agregar el número a nuestro total, lo que sea).

Ahora pues. El recorrido en primer plano (BFT) es un algoritmo, que es solo un procedimiento confiable paso a paso que garantiza producir un resultado. En este caso, se garantiza visitar todos los nodos de la gráfica que se pueda acceder desde el nodo de inicio, y no quedar atascado en ningún bucle infinito en el proceso. Aquí está:

Travesaño de primer ancho (BFT)

1. Elija un nodo de inicio.

2. Marcarlo y encolarlo en una cola vacía.

3. Si bien la cola no está vacía, siga estos pasos:

   1. Eliminar la cola del nodo frontal de la cola.

   2. Visítelo.

   3. Marcar y poner en cola todos sus nodos adyacentes sin marcar (en cualquier orden).

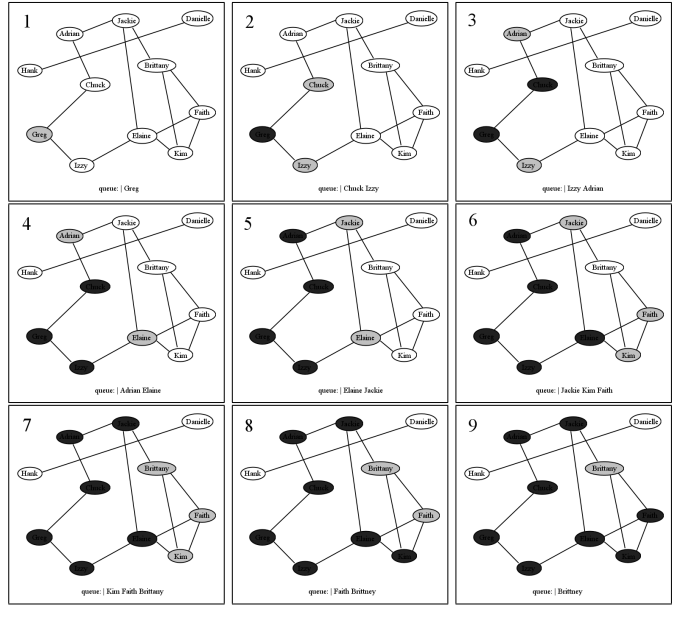
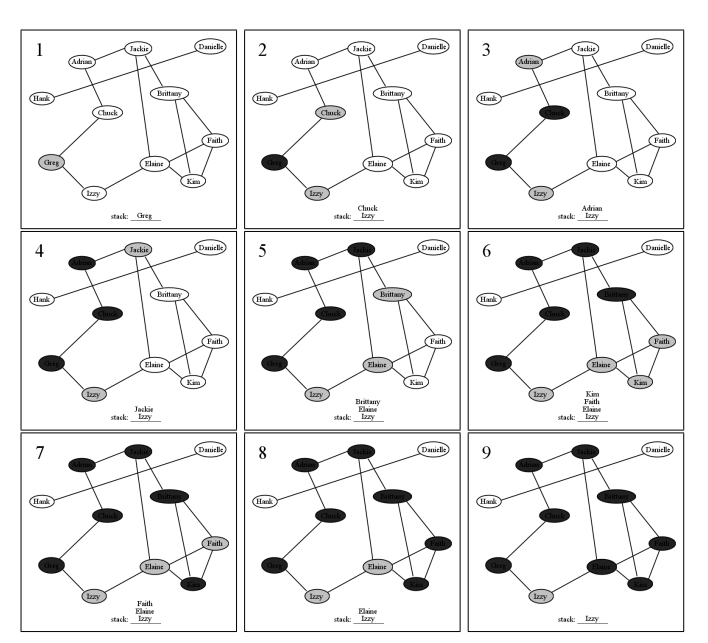
Ejecutemos este algoritmo en acción en un conjunto de usuarios de Facebook. La figura\(\PageIndex{1}\) representa once usuarios, y las amistades entre ellos. Primero, elegimos a Greg como nodo de inicio (no por ningún motivo en particular, solo que tenemos que empezar por alguna parte). Lo marcamos (en gris en el diagrama) y lo ponemos en la cola (los contenidos de la cola se listan en la parte inferior de cada fotograma, con el frente de la cola a la izquierda). Entonces, comenzamos nuestro bucle. Cuando sacamos a Greg de la cola, lo visitamos (lo que significa que “le hacemos lo que sea necesario que le hagamos a Greg”) y luego marcamos y ponemos en cola a sus nodos adyacentes Chuck e Izzy. No importa en qué orden los pusimos en la cola, así como no importaba con qué nodo iniciamos. En el panel 3, Chuck ha sido dejado de cola, visitado y sus nodos adyacentes puestos en la cola. Aquí sólo se pone en cola un nodo —Adrian— porque obviamente Greg ya ha sido marcado (e incluso visitado, nada menos) y esta marca nos permite ser inteligentes y no volver a ponerlo en cola.

Es en este punto que se hace evidente la característica de “amplitud primero”. Acabamos de terminar con Chuck, pero en lugar de explorar Adrian a continuación, retomamos con Izzy. Esto se debe a que ha estado esperando pacientemente en la cola, y su turno ha llegado. Así que dejamos a un lado a Adrian (en la cola, claro) y visitamos a Izzy, haciendo cola a su vecina Elaine en el proceso. Entonces, volvemos a Adrian. El proceso continúa, de manera “un paso en el camino superior, un paso en el camino inferior”, hasta que nuestros dos caminos de exploración realmente se encuentran en el fondo. Visitar a Jackie hace que entreguemos a Brittany, y luego cuando sacamos a Kim de la cola, no volvemos a poner en cola a Brittany porque ha sido marcada y así sabemos que ya la están cuidando.

Por consideraciones de espacio, Figure\(\PageIndex{1}\) deja fuera en este punto, pero por supuesto seguiríamos visitando nodos en la cola hasta que la cola estuviera vacía. Como puedes ver, Hank y Danielle no serán visitados en absoluto en este proceso: esto se debe a que aparentemente nadie que conozcan conoce a nadie en la multitud de Greg, y así no hay forma de llegar a ellos desde Greg. Esto es lo que quise decir antes al decir que como efecto secundario, el algoritmo BFT nos dice si la gráfica está conectada o no. Todo lo que tenemos que hacer es comenzar en alguna parte, ejecutar BFT, y luego ver si algún nodo no ha sido marcado y visitado. Si hay alguno, podemos continuar con otro punto de partida, y luego repetir el proceso.

Figura\(\PageIndex{8}\): Las etapas del recorrido ancho primero. Los nodos marcados son grises y los nodos visitados son negros. El orden de visita es: G, C, I, A, E, J, K, F, B.

Primer recorrido de profundidad (DFT)

Con el recorrido de profundidad primero, exploramos la gráfica con valentía e imprudencia. Elegimos la primera dirección que vemos, y la hundimos hasta sus profundidades, antes de retroceder a regañadientes y probar los otros caminos desde el principio.

El algoritmo es casi idéntico a BFT, excepto que en lugar de una cola, usamos una pila. Una pila es lo mismo que una cola excepto que en lugar de poner elementos en un extremo y quitárselos del otro, agregas y eliminas al mismo extremo. A este “fin” se le llama la parte superior de la pila. Cuando agregamos un elemento a este fin, decimos que lo empujamos sobre la pila, y cuando retiramos el elemento superior, decimos que lo arrancamos.

Tabla\(\PageIndex{2}\): Una pila en acción. La barra horizontal marca la parte inferior de la pila, y los elementos son empujados y reventados desde la parte superior

Comience con una pila vacía:	\(\underline{\quad}\)
Empuja un triángulo, y tenemos:	\(\underline{\triangle}\)
Empuje una estrella, y tenemos:	\(\bigstar\)\(\underline{\triangle}\)
Empuja un corazón, y tenemos:	\(\heartsuit\)\(\bigstar\)\(\underline{\triangle}\)
Pop el corazón, y tenemos:	\(\bigstar\)\(\underline{\triangle}\)
Empuje un club, y tenemos:	\(\clubsuit\)\(\bigstar\)\(\underline{\triangle}\)
Pop el club, y tenemos:	\(\bigstar\)\(\underline{\triangle}\)
Pop la estrella, y tenemos:	\(\underline{\triangle}\)
Pop el triángulo. Estamos vacíos otra vez:	\(\underline{\quad}\)

Se puede pensar en una pila como... bueno, una pila, ya sea de libros o bandejas de cafetería o cualquier otra cosa. No puedes sacar nada de la mitad de una pila, pero puedes quitarte artículos y ponerte más artículos. Mesa\(\PageIndex{2}\) tiene un ejemplo. El primer elemento empujado es siempre el último en ser reventado, y el más reciente empujado siempre está listo para ser reventado, por lo que a una pila también se le llama a veces “LIFO" (último en entrar, primero en salir).

El algoritmo de recorrido primero en profundidad se ve como déjà vu de nuevo. Todo lo que haces es reemplazar “cola” por “pila”:

Primer recorrido de profundidad (DFT)

1. Elija un nodo de inicio.

2. Marcarlo y empujarlo sobre una pila vacía.

3. Si bien la pila no está vacía, siga estos pasos:

   1. Saca el nodo superior de la pila.

   2. Visítelo.

   3. Marque y empuje todos sus nodos adyacentes sin marcar (en cualquier orden).

El algoritmo en acción se muestra en la Figura\(\PageIndex{9}\). ¡La pila realmente marcó la diferencia! En lugar de explorar alternativamente los caminos de Chuck e Izzy, se lanza tontamente por el camino de Chuck hasta donde puede llegar, hasta llegar a golpear la puerta trasera de Izzy. Sólo entonces vuelve a salir y visitar a Izzy. Esto se debe a que la pila siempre se desprende de lo que acaba de presionar, mientras que lo que sea que se empujó primero tiene que esperar hasta que todo lo demás esté hecho antes de que tenga su oportunidad. Ese primer par de empujones fue crítico: si hubiéramos empujado a Chuck antes que a Izzy desde el principio, entonces habríamos explorado el mundo entero de Izzy antes de llegar a la puerta trasera de Chuck, en lugar de al revés. Tal y como está, Izzy se puso en el fondo, y así se quedó en el fondo, lo cual es inevitable con una pila.

DFT identifica gráficos desconectados de la misma manera que BFT, y de manera similar evita quedarse atascado en bucles infinitos cuando encuentra ciclos. La única diferencia es el orden en el que visita los nodos.

Encontrar el camino más corto

Analizaremos otros dos algoritmos importantes que involucran gráficos, específicamente gráficos ponderados. El primero se llama algoritmo de ruta más corta de Dijkstra. Este es un procedimiento para encontrar la ruta más corta entre dos nodos, si existe uno. Fue inventado en 1956 por el legendario pionero de la informática Edsger Dijkstra, y es ampliamente utilizado hoy en día por, entre otras cosas, los protocolos de enrutamiento de red.

Figura\(\PageIndex{9}\): Las etapas del primer recorrido de profundidad. Los nodos marcados son grises y los nodos visitados son negros. El orden de visitas es: G, C, A, J, B, K, F, E, I.

Considere Figura\(\PageIndex{10}\), un mapa simplificado de Francia hacia noviembre de 1944. Nuevas tropas estadounidenses están llegando en barco a la ciudad portuaria de Burdeos, y necesitan llegar a Estrasburgo lo más rápido posible para ayudar a los Aliados a empujar a los escuadrones nazis de regreso a Alemania. Los vértices de esta gráfica son ciudades francesas, y los pesos de borde representan distancias de marcha en kilómetros. Aunque el Día D tuvo éxito, el desenlace de la Guerra puede depender de la rapidez con la que estos refuerzos puedan llegar al frente.

Figura\(\PageIndex{10}\): Una gráfica ponderada, a través de la cual deseamos encontrar el camino más corto de Burdeos a Estrasburgo.

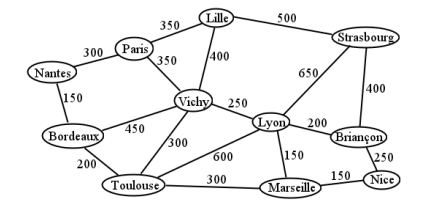
La pregunta, obviamente, es qué camino deben tomar las tropas para llegar lo más pronto posible a Estrasburgo. Con una gráfica así de pequeña, podrías ser capaz de hacer un globo ocular. (¡Pruébalo!) Pero el algoritmo de Dijksta considera sistemáticamente todos los caminos posibles, y está garantizado para encontrar el que tenga la distancia total más corta.

La forma en que funciona es asignarle a cada nodo una distancia mínima tentativa, junto con una ruta tentativa desde el nodo de inicio a él. Entonces, si el algoritmo encuentra una ruta diferente al mismo nodo a medida que avanza, actualiza esta distancia tentativa con la nueva distancia más baja, y reemplaza el “mejor camino hacia él” por el nuevo. El algoritmo de Dijkstra encuentra la distancia más corta desde el nodo de inicio hasta el nodo final, pero como un bono, en realidad encuentra la distancia más corta desde el nodo de inicio a cada nodo a medida que avanza. Así te quedas con la mejor ruta posible desde tu nodo de inicio hasta cualquier otro nodo en la gráfica.

Aquí está el algoritmo completo:

Algoritmo de ruta más corta de Dijkstra

1. Elija un nodo inicial y un nodo final.

2. Marque la distancia tentativa para los nodos iniciales como 0, y todos los demás nodos como\(\infty\).

3. Si bien todavía hay nodos no visitados, siga estos pasos:

   1. [elige] Identificar el nodo no visitado con la distancia tentativa más pequeña. (Si esto es\(\infty\) así, ya terminamos. Todos los demás nodos son inalcanzables.) Llama a este nodo el “nodo actual”.

   2. Para cada vecino no visitado del nodo actual, realice estos pasos:

      1. Calcular la suma de la distancia tentativa del nodo actual y la distancia desde el nodo actual a su vecino.

      2. Compara este total con la distancia tentativa actual del vecino. Si es menor que la distancia tentativa actual, actualice la distancia tentativa con este nuevo valor y marque una flecha en la ruta desde el nodo actual al vecino (borrando cualquier otra flecha al vecino).

      3. Marcar el nodo actual como visitado. (Su distancia y mejor camino ahora están fijos.)

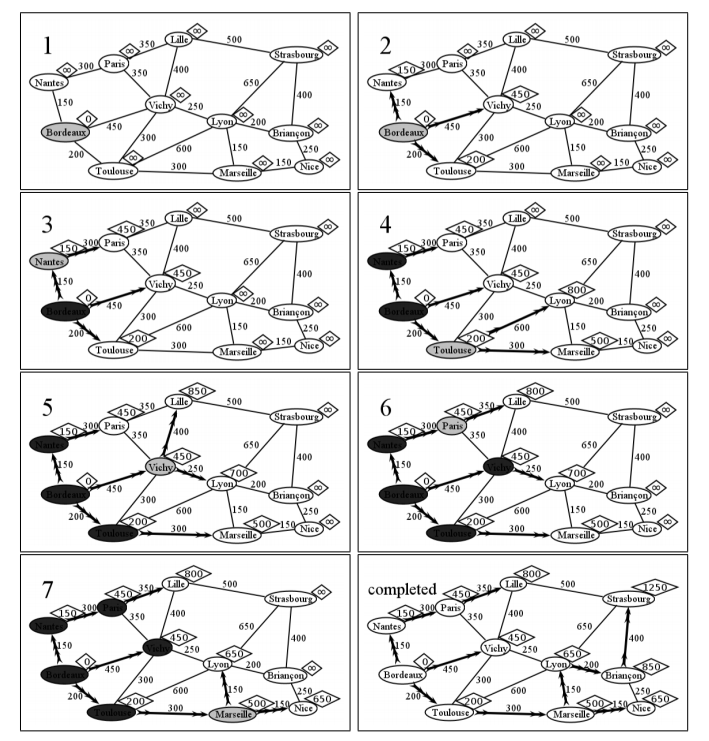
No te preocupes, esto no es tan difícil como suena. Pero sí hay que tener su ingenio sobre usted y actualizar cuidadosamente todos los números. Vamos a verlo en acción para la Francia de la Segunda Guerra Mundial. En el primer cuadro de Figura\(\PageIndex{11}\), hemos marcado cada nodo con un diamante que contiene la distancia tentativa más corta a él desde Burdeos. Esto es 0 para el propio Burdeos (ya que está a 0 kilómetros de sí mismo, duh), e infinito para todos los demás, ya que aún no hemos explorado nada, y queremos comenzar lo más pesimista posible. Actualizaremos estas distancias a valores más bajos a medida que encontremos caminos hacia ellas.

Comenzamos con Burdeos como el “nodo actual”, marcado en gris. En el marco 2, actualizamos el mejor camino posible y la distancia de ese camino para cada uno de los vecinos de Burdeos. Nantes, descubrimos, ya no está “infinito lejos”, sino a tan solo 150 km de distancia, ya que hay un camino directo hacia él desde Burdeos. Vichy y Toulouse se actualizan de manera similar. Observe las líneas pesadas con flechas en el diagrama, mostrando el mejor camino (hasta ahora) a cada una de estas ciudades desde Burdeos.

El paso 3.1 nos indica elegir el nodo con la distancia tentativa más baja como el siguiente nodo actual. Entonces para el marco 3, Nantes se ajusta a la factura con una distancia (tentativa) de 150 km. Tiene sólo un vecino sin marcar, París, que actualizamos con 450 km. ¿Por qué 450? Porque nos tomó 150 llegar desde el inicio a Nantes, y otros 300 de Nantes a París. Después de actualizar París, Nantes ahora está escrito en piedra; sabemos que nunca encontraremos una mejor ruta hacia él que desde Burdeos directamente.

El fotograma 4 es la primera vez que nos encontramos con un nodo que ya tiene una distancia tentativa no infinita. En este caso, no lo actualizamos más, porque nuestra nueva oportunidad (Burdeos —to—Toulouse—a-Vichy) es de 500 km, que es más larga que ir de Burdeos a Toulouse directo. Lyon y Marsella se actualizan con normalidad.

Ahora tenemos dos nodos sin marcar que empatan para la distancia tentativa más corta: París y Vichy (450 km cada uno). En este caso, no importa cuál escojamos. Escogeremos a Vichy sin ningún motivo en particular. El fotograma 5 muestra entonces alguna actividad interesante. No actualizamos el camino a París, ya que sería 800 km a través de Vichy, mientras que París ya tenía un camino mucho mejor de 450 km. Lille se actualiza del infinito a 850 km, ya que encontramos nuestro primer camino hacia él. Pero Lyon es el caso realmente interesante. Ya tenía un camino —Burdeos— a —Toulouse—a-Lyon— pero ese camino era de 800 km, y acabamos de encontrar un camino mejor: Burdeos —a-Vicy—a-Lyon, que sólo cuesta 450 + 250 = 700. Esto significa que retiramos la flecha de Toulouse a Lyon y dibujamos una nueva flecha de Vichy a Lyon. Tenga en cuenta que la flecha de Burdeos a Toulouse no desaparece, a pesar de que formaba parte de este camino aparentemente no tan bueno hacia Lyon. Eso es porque la mejor ruta a Toulouse sigue siendo por ese borde. El hecho de que no lo usáramos para ir a Lyon no significa que no lo queramos si íbamos simplemente a Toulouse.

En el marco 6, tomamos el otro nodo 450 (París) que descuidamos temporalmente cuando elegimos al azar continuar primero con Vichy. Cuando lo hacemos, descubrimos un mejor camino hacia Lille que antes, y así actualizamos su distancia (a 800 km) y su camino (a través de Nantes y París en lugar de por Vichy) en consecuencia.

Cuando consideramos Marsella en el marco 7, encontramos otro camino mejor: esta vez a Lyon. Olvídate de eso a través de cosas de Vichy; resulta ser un poco más rápido pasar por Toulouse y Marsella. En otras noticias, encontramos el camino a Niza.

Ojalá consigas el patrón. Seguimos seleccionando el nodo sin marcar con la menor distancia tentativa, actualizando las distancias y caminos de sus vecinos, marcándolo como “visitado”, hasta que terminemos con todos los nodos. El último fotograma muestra la versión terminada (con todos los nodos coloreados de blanco nuevamente para que puedas leerlos). El veredicto es: nuestras tropas deberían ir de Burdeos a través de Toulouse, Marsella, Lyon y Briançon en su camino a los combates en Strasborg, para un total de 1.250 kilómetros. ¿Quién sabía? Todos los demás caminos son más largos. Observe también cómo en la figura, la distancia más corta a cada nodo se identifica fácilmente al observar las líneas con flechas pesadas.

Encontrar el conjunto mínimo de bordes de conexión

Así que hemos descubierto el camino más corto para nuestras tropas. Pero nuestros generales de campo también podrían querer hacer algo diferente: establecer líneas de suministro. Una línea de suministro es una ruta segura por la que se pueden entregar alimentos, combustible y maquinaria, con un recorrido suave y protección contra emboscadas. Ahora tenemos divisiones militares estacionadas en cada una de las once ciudades francesas, y así todas las ciudades deben estar conectadas entre sí a través de caminos seguros. Sin embargo, salvaguardar cada milla de una línea de suministro requiere recursos, así que queremos hacerlo de la manera mínima posible. ¿Cómo podemos conectar todas las ciudades entre sí para que podamos entregar suministros de manera segura entre cualquiera de ellas, utilizando la menor cantidad posible de carretera?

Esto no es sólo un problema militar. El mismo tema surgió en la antigua Roma cuando los acueductos tuvieron que llegar a múltiples ciudades. Más recientemente, suministrar energía a vecindarios y hogares, o conectar en red múltiples computadoras con cable Ethernet, implica la misma pregunta. En todos estos casos, no estamos tras la ruta más corta entre dos puntos. En cambio, estamos más o menos después de la ruta más corta “entre todos los puntos”. No nos importa cómo se conecte cada par de nodos, siempre que estén conectados. Y es la longitud total de las conexiones requeridas lo que queremos minimizar.

Para encontrar esto, usaremos el algoritmo de Prim, una técnica que lleva el nombre del informático algo oscuro Robert Prim que la desarrolló en 1957, aunque ya había sido descubierta mucho antes (1930, por el matemático checo Vojtech Jarnik). El algoritmo de Prim resulta ser mucho más fácil de llevar a cabo que el algoritmo de Dijkstra, lo cual me parece sorprendente, ya que parece estar resolviendo un problema que es igual de difícil. Pero aquí está todo lo que haces:

Algoritmo de conjunto de bordes de conexión mínimo de Pri

1. Elija un nodo, cualquier nodo.

2. Si bien no todos los nodos están conectados, siga estos pasos:

   1. [greedystep] Identifica el nodo más cercano a los nodos ya conectados y conéctelo a esos nodos a través del borde más corto.

Eso es. El algoritmo de Prim es un ejemplo de un algoritmo codicioso, lo que significa que siempre elige la mejor opción inmediatamente obvia a corto plazo disponible. Los algoritmos no codiciosos pueden decir, “aunque hacer X daría la mayor satisfacción a corto plazo, puedo mirar hacia adelante y ver que elegir Y en su lugar conducirá a un mejor resultado general a largo plazo”. Los algoritmos codiciosos, por el contrario, siempre engullan lo que parece mejor en su momento. Eso es lo que está haciendo el algoritmo de Prim en el paso 2.1. Busca el nodo no conectado que está inmediatamente más cerca del grupo conectado, y lo agrega sin pensarlo dos veces. No hay noción de “tal vez voy a obtener un conjunto de borde general más corto si dejo de conectar este nodo tentadoramente cercano en este momento”.

A veces, un algoritmo codicioso resulta dar un resultado óptimo. A menudo no lo hace, y los enfoques más sofisticados pueden encontrar mejores soluciones. En este caso, pasa a darse cuenta de que el enfoque codicioso sí funciona! El algoritmo de Prim siempre encontrará el conjunto de bordes que conecta todos los nodos y lo hace con la menor distancia total posible. Es increíble que pueda hacerlo, sobre todo porque nunca retrocede ni revisa su opinión como lo hace el algoritmo de Dijkstra.

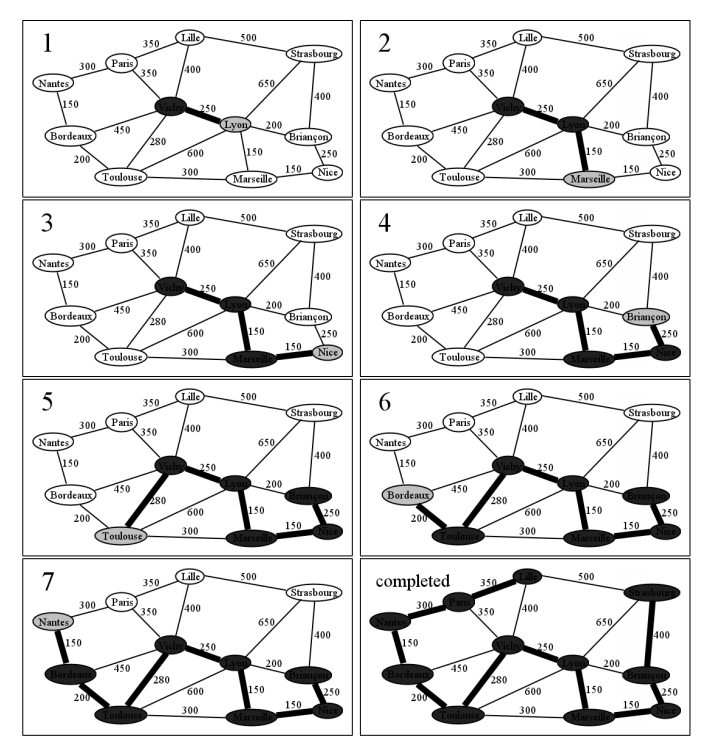
Sigamos el progreso del algoritmo en el ejemplo de la Segunda Guerra Mundial. Podemos comenzar con cualquier nodo, así que elegiremos a Vichy justo al azar. El cuadro 1 de la Figura\(\PageIndex{12}\) muestra lo que sucede cuando el algoritmo comienza con Vichy: simplemente examinamos a todos sus vecinos, y conectamos el que está más cerca de él. Nada podría ser más sencillo. En este caso, Lyon está a apenas 250 km de distancia, lo que está más cerca que cualquier otra cosa de Vichy, así que lo conectamos y agregamos el borde Vichy-Lyon a nuestro conjunto de bordes. En la figura se muestra una línea negra pesada entre Vichy y Lyon para demostrar que oficialmente será una línea de suministro.

Y así va. En cuadros sucesivos, agregamos Marsella, Niza y Briançon al conjunto de nodos conectados, ya que no podemos hacer mejor que 150 km, 150 km y 250 km, respectivamente. Tenga en cuenta que en el marco 5 no oscurecemos el borde entre Lyon y Briançon, a pesar de que 200 km es el borde conectado más corto, debido a que esos nodos ya se han conectado previamente. Tenga en cuenta también que el algoritmo puede saltar de lado a lado; no estamos buscando el borde más corto del nodo agregado más recientemente, sino el borde más corto de cualquier nodo conectado.

El resultado final se muestra en el último fotograma. Esta es la mejor manera de conectar todas las ciudades entre sí, si “mejor” significa “menor distancia total de la línea de suministro”. Pero si miras con atención, notarás algo fascinante. ¡Esta red de aristas no contiene el camino más corto de Burdeos a Estrasburgo! Ese resultado me parece estupefacto. ¿No pensarías que el camino más corto entre dos nodos cualquiera aterrizaría justo en esta red Prim? Sin embargo, si comparas Figura\(\PageIndex{12}\) con Figura\(\PageIndex{11}\) verás que la forma más rápida de llegar a Strasborg es directamente por Marsella, no por Vichy.

Por lo que terminamos con el notable hecho de que la ruta más corta entre dos puntos no tiene nada que ver con la distancia total más corta entre todos los puntos. ¿Quién sabía?

Figura\(\PageIndex{11}\): Las etapas del algoritmo de ruta más corta de Dijkstra. El “nodo actual” se muestra en gris, con los nodos visitados (cuyos mejores caminos y distancias más cortas se han determinado inalterablemente) en negro. El diamante al lado de cada nodo muestra la distancia tentativa más corta a ese nodo desde Burdeos.

Figura\(\PageIndex{12}\): Las etapas del algoritmo de conjunto mínimo de borde de conexión de Prim. Las líneas pesadas indican bordes que se han agregado (irrevocablemente) al conjunto.

 

 

 

---

1. La frase “cero o más” es común en las matemáticas discretas. En este caso, indica que la gráfica vacía, que no contiene ningún vértice, sigue siendo una gráfica legítima.
2. También diremos que un ciclo no puede repetir ningún borde o vértice a lo largo del camino, de manera que no pueda ir y venir repetidamente e inútilmente entre dos nodos adyacentes. Algunos matemáticos llaman a esto un ciclo simple para distinguirlo del ciclo más general, pero solo diremos que ningún ciclo puede repetirse así.