5.2: Árboles
- Page ID
- 117616
Un árbol no es realmente más que una simplificación de una gráfica. Hay dos tipos de árboles en el mundo: árboles libres y árboles enraizados. 1
Árboles libres
Un árbol libre es solo una gráfica conectada sin ciclos. Cada nodo es accesible desde los demás, y solo hay una manera de llegar a cualquier parte. Echa un vistazo a Figura\(\PageIndex{1}\). Se ve como una gráfica (y lo es) pero a diferencia de la gráfica de Francia de la Segunda Guerra Mundial, es más esquelética. Esto se debe a que en cierto sentido, un árbol libre no contiene nada “extra”.
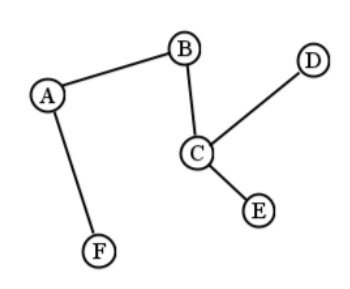
Si tienes un árbol libre, los siguientes datos interesantes son ciertos:
-
Hay exactamente una ruta entre dos nodos cualesquiera. (¡Compruébalo!)
-
Si elimina cualquier borde, la gráfica se desconecta. (¡Pruébalo!)
-
Si agregas algún borde nuevo, terminas agregando un ciclo. (¡Pruébalo!)
-
[onelessedge] Si hay\(n\) nodos, hay\(n-1\) bordes. (¡Piénsalo!)
Entonces, básicamente, si tu objetivo es conectar todos los nodos, y tienes un árbol libre, ya estás listo. Agregar cualquier cosa es redundante, y quitarle cualquier cosa lo rompe.
Si esto te recuerda el algoritmo de Prim, debería. El algoritmo de Prim produjo exactamente esto: un árbol libre que conecta todos los nodos, y específicamente el árbol libre con la longitud total más corta posible. Regresa y mira el fotograma final de la Figura 5.1.12 y convencerse de que los bordes oscurecidos forman un árbol libre.
Por esta razón, el algoritmo a menudo se llama algoritmo de árbol de expansión mínimo de Prim. Un “árbol de expansión” solo significa “un árbol libre que abarca (conecta) todos los nodos de la gráfica”.
Ten en cuenta que hay muchos árboles libres que uno puede hacer con el mismo conjunto de vértices. Por ejemplo, si eliminas el borde de A a F, y agregas uno de cualquier otra cosa a F, tienes un árbol libre diferente.
Árboles enraizados
Ahora un árbol enraizado es lo mismo que un árbol libre, excepto que elevamos un nodo para convertirnos en la raíz. Resulta que esto hace toda la diferencia. Supongamos que elegimos A como la raíz de la Figura\(\PageIndex{1}\). Entonces tendríamos el árbol enraizado en la mitad izquierda de Figura\(\PageIndex{2}\). El vértice A se ha posicionado en la parte superior, y todo lo demás fluye debajo de él. Pienso en ello como llegar al árbol libre, agarrar cuidadosamente un nudo, y luego levantar la mano para que el resto del árbol libre colgue de ahí. Si hubiéramos elegido (digamos) C como raíz en su lugar, tendríamos un árbol enraizado diferente, representado en la mitad derecha de la figura. Ambos árboles enraizados tienen todos los mismos bordes que el árbol libre: B está conectado tanto a A como a C, F está conectado solo a A, etc. La única diferencia es qué nodo se designa la raíz.
Hasta ahora hemos dicho que el posicionamiento espacial en las gráficas es irrelevante. Pero esto cambia un poco con los árboles enraizados. El posicionamiento vertical es nuestra única manera de mostrar qué nodos están “por encima” de otros, y la palabra “arriba” sí tiene sentido aquí: significa más cerca de la raíz. La altitud de un nodo muestra cuántos pasos está lejos de la raíz. En el árbol enraizado derecho, los nodos B, D y E están todos a un paso de la raíz (C), mientras que el nodo F está a tres pasos de distancia.
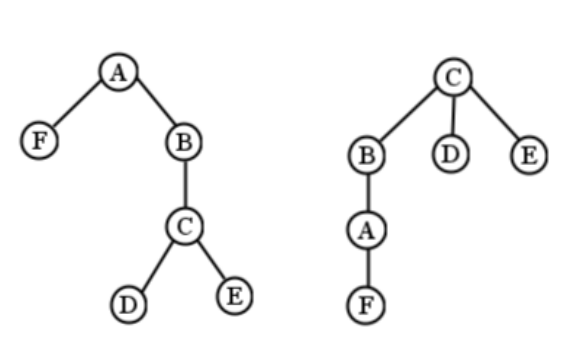
El aspecto clave de los árboles enraizados —que es tanto su mayor ventaja como su mayor limitación— es que cada nodo tiene uno y solo un camino hacia la raíz. Este comportamiento se hereda de los árboles libres: como señalamos, cada nodo tiene solo una ruta entre sí.
Los árboles tienen una gran variedad de aplicaciones. Piense en los archivos y carpetas de su disco duro: en la parte superior está la raíz del sistema de archivos (tal vez “/" en Linux/Mac o “C:\\” en Windows) y debajo de eso se nombran carpetas. Cada carpeta puede contener archivos así como otras carpetas con nombre, y así sucesivamente en la jerarquía. El resultado es que cada archivo tiene una, y solo una, ruta distinta desde la parte superior del sistema de archivos. El archivo puede ser almacenado, y posteriormente recuperado, exactamente de una manera.
Un “organigrama” es así: el CEO está en la cima, luego debajo de ella están los VP, los Directores, los Gerentes y finalmente los empleados de base. Así es una organización militar: el Comandante en Jefe dirige generales, que comandan coroneles, que comandan mayores, quienes comandan capitanes, quienes comandan tenientes, quienes comandan sargentos, quienes comandan soldados.
El cuerpo humano es incluso una especie de árbol enraizado: contiene sistemas esqueléticos, cardiovasculares, digestivos y otros, cada uno de los cuales está compuesto por órganos, luego tejidos, luego células, moléculas y átomos. De hecho, cualquier cosa que tenga este tipo de jerarquía de contención parcial es solo pedir ser representado como un árbol.
En la programación informática, las aplicaciones son demasiado numerosas para nombrarlas. Los compiladores escanean código y construyen un “árbol de análisis” de su significado subyacente. HTML es una forma de estructurar el texto plano en una jerarquía similar a un árbol de elementos visualizables. Los programas de ajedrez de IA construyen árboles que representan sus posibles movimientos futuros y las probables respuestas de su oponente, con el fin de “ver muchos movimientos adelante” y evaluar sus mejores opciones. Los diseños orientados a objetos implican “jerarquías de herencia” de clases, cada una especializada de otra específica. Etc. Aparte de una secuencia simple (como una matriz), los árboles son probablemente la estructura de datos más común en toda la informática.
Terminología de árboles arraig
Los árboles enraizados llevan consigo una serie de términos. Voy a usar el árbol del lado izquierdo de la Figura\(\PageIndex{2}\) como una ilustración de cada uno:
raíz.
El nodo en la parte superior del árbol, que es A en nuestro ejemplo. Tenga en cuenta que a diferencia de los árboles en el mundo real, los árboles de informática tienen su raíz en la parte superior y crecen hacia abajo. Cada árbol tiene una raíz excepto el árbol vacío, que es el “árbol” que no tiene ningún nodo en él. (Es un poco raro pensar en “nada” como un árbol, pero es como el conjunto vacío\(\varnothing\), que sigue siendo un conjunto.)
padre.
Cada nodo excepto la raíz tiene un padre: el nodo inmediatamente por encima de él. El padre de D es C, el padre de C es B, el padre de F es A y A no tiene padre.
niño.
Algunos nodos tienen hijos, que son nodos conectados directamente debajo de él. Los hijos de A son F y B, C son D y E, el único hijo de B es C y E no tiene hijos.
hermano.
Un nodo con el mismo padre. El hermano de E es D, B es F y ninguno de los otros nodos tiene hermanos.
antepasado.
Tu padre, abuelo, bisabuelo, etc., todo el camino de regreso a la raíz. El único ancestro de B es A, mientras que los ancestros de E son C, B y A. Tenga en cuenta que F no es el antepasado de C, aunque esté por encima de él en el diagrama: no hay conexión de C a F, excepto de vuelta a través de la raíz (que no cuenta).
descendiente.
Tus hijos, nietos, bisnietos, etc., hasta el final las hojas. Los descendientes de B son C, D y E, mientras que A son F, B, C, D y E.
hoja.
Un nodo sin hijos. F, D y E son hojas. Tenga en cuenta que en un árbol (muy) pequeño, la raíz podría ser en sí misma una hoja.
nodo interno.
Cualquier nodo que no sea una hoja. A, B y C son los nodos internos en nuestro ejemplo.
profundidad (de un nodo).
La profundidad de un nodo es la distancia (en número de nodos) desde éste hasta la raíz. La raíz en sí tiene profundidad cero. En nuestro ejemplo, B es de profundidad 1, E es de profundidad 3 y A es de profundidad 0.
altura (de un árbol).
La altura de un árbol enraizado es la profundidad máxima de cualquiera de sus nodos; es decir, la distancia máxima desde la raíz hasta cualquier nodo. Nuestro ejemplo tiene una altura de 3, ya que los nodos “más profundos” son D y E, cada uno con una profundidad de 3. Se considera que un árbol con un solo nodo tiene una altura de 0. Extrañamente, pero para ser consistentes, diremos que el árbol vacío tiene altura -1! Extraño, pero ¿qué más podría ser? Decir que tiene altura 0 parece inconsistente con un árbol de un nodo que también tiene altura 0. En todo caso, esto no va a surgir mucho.
nivel.
Todos los nodos con la misma profundidad se consideran en el mismo “nivel”. B y F están en el nivel 1, y D y E están en el nivel 3. Los nodos en el mismo nivel no son necesariamente hermanos. Si F tuviera un hijo llamado G en el diagrama de ejemplo, entonces G y C estarían en el mismo nivel (2), pero no serían hermanos porque tienen padres diferentes. (Podríamos llamarlos “primos” para continuar con la analogía familiar.)
subárbol.
Por último, gran parte de lo que da a los árboles su poder expresivo es su naturaleza recursiva. Esto significa que un árbol está formado por otros árboles (más pequeños). Considera nuestro ejemplo. Es un árbol con una raíz de A. ¡Pero los dos hijos de A son cada uno árboles por derecho propio! F en sí es un árbol con un solo nodo. B y sus descendientes hacen otro árbol con cuatro nodos. Consideramos que estos dos árboles son subárboles del árbol original. La noción de “raíz” cambia un poco a medida que consideramos subárboles: A es la raíz del árbol original, pero B es la raíz del segundo subárbol. Cuando consideramos a los hijos de B, vemos que hay otro subárbol más, que tiene sus raíces en C. Y así sucesivamente. Es fácil ver que cualquier subárbol cumple con todas las propiedades de los árboles, y así todo lo que hemos dicho anteriormente se aplica también a él.
Árboles binarios (BT's)
Los nodos en un árbol enraizado pueden tener cualquier número de hijos. Sin embargo, hay un tipo especial de árbol enraizado llamado árbol binario que restringimos simplemente diciendo que cada nodo puede tener como máximo dos hijos. Además, etiquetaremos a cada uno de estos dos niños como “niño izquierdo” y “niño derecho”. (Tenga en cuenta que un nodo en particular bien podría tener solo un hijo izquierdo, o solo un hijo derecho, pero aún así es importante saber en qué dirección está ese niño).
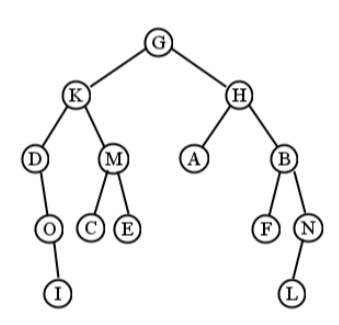
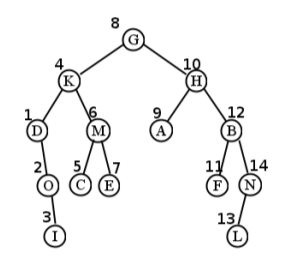
La mitad izquierda de la Figura\(\PageIndex{2}\) es un árbol binario, pero la mitad derecha no lo es (C tiene tres hijos). Un árbol binario más grande (de altura 4) se muestra en la Figura\(\PageIndex{3}\).
Atravesando árboles binarios
Había dos formas de atravesar una gráfica: primero en ancho y primero en profundidad. Curiosamente, hay tres formas de atravesar un árbol: pre-order, post-order y in-order. Los tres comienzan en la raíz, y los tres consideran a cada uno de los hijos de la raíz como subárboles. La diferencia está en el orden de las visitas.
-
Visita la raíz.
-
Tratar al niño izquierdo y a todos sus descendientes como un subárbol, y recorrerlo en su totalidad.
-
Haz lo mismo con el hijo adecuado.
Es complicado porque hay que recordar que cada vez que “tratas a un niño como un subárbol” haces todo el proceso de recorrido en ese subárbol. Esto implica recordar dónde estabas una vez que terminaste.
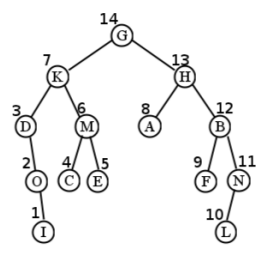
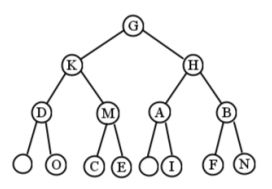
Sigue este ejemplo cuidadosamente. Para el árbol en la Figura\(\PageIndex{3}\), comenzamos visitando G. Luego, atravesamos todo el “subárbol K”. Esto implica visitar la propia K, y luego atravesar todo su subárbol izquierdo (anclado en D). Después de visitar el nodo D, descubrimos que en realidad no tiene subárbol izquierdo, así que seguimos adelante y atravesamos su subárbol derecho. Esto visita O seguido de I (ya que O tampoco tiene subárbol izquierdo) que finalmente regresa de nuevo por la escalera.
Es en este punto donde es fácil perderse. Terminamos de visitarme, y luego tenemos que preguntar “bien, ¿dónde carajo estábamos? ¿Cómo llegamos hasta aquí?” La respuesta es que acabábamos de estar en el nodo K, donde habíamos atravesado su subárbol izquierdo (D). Entonces, ¿qué es el momento de hacer? Atraviesa el subárbol derecho, claro, que es M. Esto implica visitar M, C y E (en ese orden) antes de regresar a la cima, G.
Ahora estamos en el mismo tipo de situación en la que podríamos habernos perdido antes: hemos pasado mucho tiempo en el enredado lío del subárbol izquierdo de G, y solo tenemos que recordar que ahora es el momento de hacer el subárbol derecho de G. Sigue este mismo procedimiento, y todo el orden de visitas termina siendo: G, K, D, O, I, M, C, E, H, A, B, F, N, L. (Ver Figura\(\PageIndex{4}\) para una visual.)
-
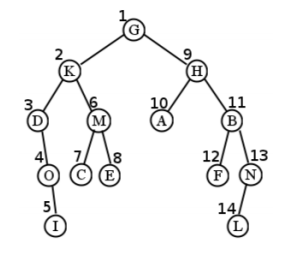
Tratar al niño izquierdo y a todos sus descendientes como un subárbol, y recorrerlo en su totalidad.
-
Haz lo mismo con el hijo adecuado.
-
Visita la raíz.
Es lo mismo que pre-order, excepto que visitamos la raíz después de los niños en lugar de antes. Aún así, a pesar de su similitud, ésta siempre ha sido la más difícil para mí. Todo parece pospuesto, y hay que recordar en qué orden hacerlo después.
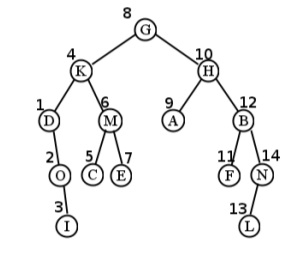
Para nuestro árbol de muestra, el primer nodo visitado resulta ser I. Esto se debe a que tenemos que posponer la visita a G hasta que terminemos su subárbol izquierdo (y derecho); luego posponemos K hasta que terminemos su subárbol izquierdo (y derecho); posponer D hasta que terminemos con el subárbol de O, y posponemos O hasta que hagamos I. Luego, finalmente, el la cosa comienza a relajarse... todo el camino de regreso a K. Pero en realidad no podemos visitar a la propia K todavía, porque tenemos que hacer su subárbol correcto. Esto da como resultado C, E y M, en ese orden. Entonces podemos hacer K, pero aún no podemos hacer G porque tenemos todo el mundo de su subárbol derecho con el que enfrentarnos. Todo el orden termina siendo: I, O, D, C, E, M, K, A, F, L, N, B, H, y finalmente G. (Ver Figura\(\PageIndex{5}\) para una visual.)
Tenga en cuenta que esto no es remotamente lo contrario de la visita de pre-orden, como es de esperar. G es último en lugar de primero, pero el resto está todo desordenado.
-
Tratar al niño izquierdo y a todos sus descendientes como un subárbol, y recorrerlo en su totalidad.
-
Visita la raíz.
-
Atraviesa el subárbol derecho en su totalidad.
Entonces, en lugar de visitar la raíz primero (pre-order) o last (post-order) la tratamos entre nuestros hijos izquierdo y derecho. Esto puede parecer algo extraño de hacer, pero hay un método para la locura que quedará claro en la siguiente sección.
Para el árbol de muestra, el primer nodo visitado es D. Esto se debe a que es el primer nodo encontrado que no tiene un subárbol izquierdo, lo que significa que el paso 1 no necesita hacer nada. A esto le siguen O y yo, por la misma razón. Luego visitamos K antes de su subárbol derecho, que a su vez visita C, M y E, en ese orden. El orden final es: D, O, I, K, C, M, E, G, A, H, F, B, L, N. (Ver Figura\(\PageIndex{6}\).)
Si sus nodos están espaciados uniformemente, puede leer el recorrido en orden del diagrama moviendo los ojos de izquierda a derecha. Sin embargo, ten cuidado con esto porque en última instancia la posición espacial no importa, sino más bien las relaciones entre los nodos. Por ejemplo, si hubiera dibujado el nodo I más a la derecha, para hacer menos empinadas las líneas entre D—O—I, ese nodo I podría haber sido empujado físicamente a la derecha de K. Pero eso no cambiaría el orden y K lo había visitado antes.
Por último, cabe mencionar que todos estos métodos transversales hacen un uso elegante de la recursión. La recursión es una forma de tomar un problema grande y dividirlo en subproblemas similares, pero más pequeños. Entonces, cada uno de esos subproblemas puede ser atacado de la misma manera que atacaste al problema mayor: dividiéndolos en subproblemas. Todo lo que necesitas es una regla para eventualmente detener el proceso de “ruptura” haciendo algo realmente.
Cada vez que uno de estos procesos transversales trata a un hijo izquierdo o derecho como un subárbol, están “recurriendo” al reiniciar todo el proceso de recorrido en un árbol más pequeño. El recorrido por pre-orden, por ejemplo, después de visitar la raíz, dice: “bien, pretendamos que comenzamos todo este asunto del recorrido con el árbol más pequeño enraizado en mi hijo izquierdo. Una vez que eso haya terminado, despiértame para que pueda iniciarlo de manera similar con mi hijo adecuado”. La recursión es una forma muy común y útil de resolver ciertos problemas complejos, y los árboles están plagados de oportunidades.
Tamaños de árboles binarios
Los árboles binarios pueden ser de cualquier forma vieja irregular, como nuestro\(\PageIndex{3}\) ejemplo de Figura. A veces, sin embargo, queremos hablar de árboles binarios con una forma más regular, que satisfacen ciertas condiciones. En particular, hablaremos de tres tipos especiales:
árbol binario completo.
Un árbol binario completo es aquel en el que cada nodo (excepto las hojas) tiene dos hijos. Dicho de otra manera, cada nodo tiene dos hijos o ninguno: no se permite la rigurosidad. La figura no\(\PageIndex{3}\) está llena, pero lo sería si agregáramos los tres nodos en blanco en la Figura\(\PageIndex{7}\).
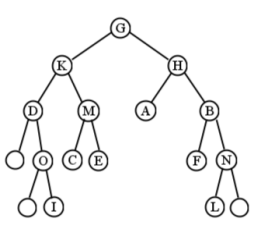
Por cierto, no siempre es posible tener un árbol binario completo con un número particular de nodos. Por ejemplo, un árbol binario con dos nodos, no puede estar lleno, ya que inevitablemente tendrá una raíz con un solo hijo.
árbol binario completo.
Un árbol binario completo es aquel en el que cada nivel tiene todos los nodos posibles presentes, excepto quizás el nivel más profundo, que se llena todo el camino desde la izquierda. La figura no\(\PageIndex{7}\) está llena, pero lo sería si la arregláramos como en la Figura\(\PageIndex{8}\).
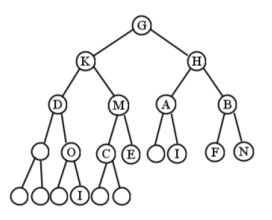
A diferencia de los árboles binarios completos, siempre es posible tener un árbol binario completo sin importar cuántos nodos contenga. Simplemente sigues rellenando de izquierda a derecha, nivel tras nivel.
árbol binario perfecto.
Nuestro último tipo especial tiene un título bastante audaz, pero un árbol “perfecto” es simplemente uno que está exactamente equilibrado: cada nivel está completamente lleno. La figura no\(\PageIndex{8}\) es perfecta, pero sería si agregáramos nodos para llenar el nivel 4, o eliminamos la parte inconclusa del nivel 3 (como en la Figura)\(\PageIndex{9}\).
Los árboles binarios perfectos obviamente tienen las restricciones de tamaño más estrictas. Solo es posible, de hecho, tener árboles binarios perfectos con\(2^{h+1}-1\) nodos, si\(h\) es la altura del árbol. Entonces hay árboles binarios perfectos con 1, 3, 7, 15, 31,... nodos, pero ninguno en el medio. En cada uno de esos árboles,\(2^h\) de los nodos (casi exactamente la mitad) son hojas.
Ahora como veremos, los árboles binarios pueden poseer algunos poderes bastante sorprendentes si los nodos dentro de ellos están organizados de ciertas maneras. Específicamente, un árbol de búsqueda binaria y un montón son dos tipos especiales de árboles binarios que se ajustan a restricciones específicas. En ambos casos, lo que los hace tan poderosos es la velocidad a la que un árbol crece a medida que se le agregan nodos.
Supongamos que tenemos un árbol binario perfecto. Para hacerlo concreto, digamos que tiene altura 3, lo que le daría 1+2+4+8=15 nodos, 8 de los cuales son hojas. Ahora, ¿qué pasa si aumentas la altura de este árbol a 4? Si todavía es un árbol “perfecto”, habrás agregado 16 nodos más (todas las hojas). Así se ha duplicado el número de hojas simplemente agregando un nivel más. Esto cae en cascada cuantos más niveles agregues. Un árbol de altura 5 vuelve a duplicar el número de hojas (a 32), y la altura 6 lo vuelve a duplicar (a 64).
Si esto no te parece increíble, probablemente sea porque no aprecias completamente lo rápido que puede acumularse este tipo de crecimiento exponencial. Supongamos que tenías un árbol binario perfecto de altura 30, ciertamente no una figura impresionante. Uno podría imaginarlo encajando en una hoja de papel... en cuanto a la altura, es decir. Pero corre los números y descubrirás que tal árbol habría terminado, más de uno por cada persona en Estados Unidos. Aumenta la altura del árbol a solo 34 —solo 4 niveles adicionales— y de repente tienes más de 8 mil millones de hojas, fácilmente mayores que la población del planeta Tierra.
El poder de crecimiento exponencial sólo se alcanza plenamente cuando el árbol binario es perfecto, ya que un árbol con algunos nodos internos “faltantes” no lleva la capacidad máxima de la que es capaz. Tiene algunos agujeros en él. Aún así, mientras el árbol sea bastante tupido (es decir, no está horriblemente desequilibrado en solo unas pocas áreas) el enorme crecimiento pronosticado para árboles perfectos sigue siendo aproximadamente el caso.
La razón por la que esto se llama crecimiento “exponencial” es que la cantidad que estamos variando —la altura— aparece como exponente en el número de hojas, que es\(2^h\). Cada vez que añadimos un solo nivel, duplicamos el número de hojas.
Entonces el número de hojas (llámalo\(l\)) es\(2^h\), si\(h\) es la altura del árbol. Volteando esto, decimos eso\(h = \lg(l)\). La función “lg” es un logaritmo, específicamente un logaritmo con base-2. Esto es lo que suelen utilizar los informáticos, en lugar de una base de 10 (que se escribe “log”) o una base de\(e\) (que se escribe “ln”). Ya que\(2^h\) crece muy, muy rápido, se deduce que\(\lg(l)\) crece muy, muy lentamente. Después de que nuestro árbol alcance algunos millones de nodos, podemos agregar más y más nodos sin crecer la altura del árbol significativamente en absoluto.
El mensaje para llevar aquí es simplemente que una cantidad increíblemente grande de nodos se pueden acomodar en un árbol con una altura muy modesta. Esto permite, entre otras cosas, buscar una gran cantidad de información asombrosamente rápidamente... siempre que el contenido del árbol esté organizado correctamente.
Árboles binarios (BT's)
Los nodos en un árbol enraizado pueden tener cualquier número de hijos. Sin embargo, hay un tipo especial de árbol enraizado llamado árbol binario que restringimos simplemente diciendo que cada nodo puede tener como máximo dos hijos. Además, etiquetaremos a cada uno de estos dos niños como “niño izquierdo” y “niño derecho”. (Tenga en cuenta que un nodo en particular bien podría tener solo un hijo izquierdo, o solo un hijo derecho, pero aún así es importante saber en qué dirección está ese niño).
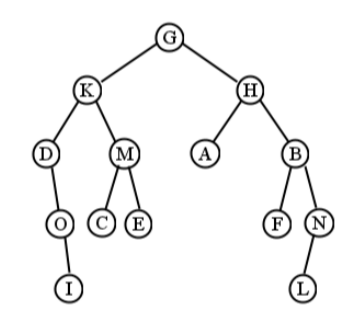
La mitad izquierda de la Figura\(\PageIndex{9}\) es un árbol binario, pero la mitad derecha no lo es (C tiene tres hijos). Un árbol binario más grande (de altura 4) se muestra en la Figura\(\PageIndex{10}\).
Atravesando árboles binarios
Había dos formas de atravesar una gráfica: primero en ancho y primero en profundidad. Curiosamente, hay tres formas de atravesar un árbol: pre-order, post-order y in-order. Los tres comienzan en la raíz, y los tres consideran a cada uno de los hijos de la raíz como subárboles. La diferencia está en el orden de las visitas.
-
Visita la raíz.
-
Tratar al niño izquierdo y a todos sus descendientes como un subárbol, y recorrerlo en su totalidad.
-
Haz lo mismo con el hijo adecuado.
Es complicado porque hay que recordar que cada vez que “tratas a un niño como un subárbol” haces todo el proceso de recorrido en ese subárbol. Esto implica recordar dónde estabas una vez que terminaste.
Sigue este ejemplo cuidadosamente. Para el árbol en la Figura\(\PageIndex{10}\), comenzamos visitando G. Luego, atravesamos todo el “subárbol K”. Esto implica visitar la propia K, y luego atravesar todo su subárbol izquierdo (anclado en D). Después de visitar el nodo D, descubrimos que en realidad no tiene subárbol izquierdo, así que seguimos adelante y atravesamos su subárbol derecho. Esto visita O seguido de I (ya que O tampoco tiene subárbol izquierdo) que finalmente regresa de nuevo por la escalera.
Es en este punto donde es fácil perderse. Terminamos de visitarme, y luego tenemos que preguntar “bien, ¿dónde carajo estábamos? ¿Cómo llegamos hasta aquí?” La respuesta es que acabábamos de estar en el nodo K, donde habíamos atravesado su subárbol izquierdo (D). Entonces, ¿qué es el momento de hacer? Atraviesa el subárbol derecho, claro, que es M. Esto implica visitar M, C y E (en ese orden) antes de regresar a la cima, G.
Ahora estamos en el mismo tipo de situación en la que podríamos habernos perdido antes: hemos pasado mucho tiempo en el enredado lío del subárbol izquierdo de G, y solo tenemos que recordar que ahora es el momento de hacer el subárbol derecho de G. Sigue este mismo procedimiento, y todo el orden de visitas termina siendo: G, K, D, O, I, M, C, E, H, A, B, F, N, L. (Ver Figura\(\PageIndex{11}\) para una visual.)
-
Tratar al niño izquierdo y a todos sus descendientes como un subárbol, y recorrerlo en su totalidad.
-
Haz lo mismo con el hijo adecuado.
-
Visita la raíz.
Es lo mismo que pre-order, excepto que visitamos la raíz después de los niños en lugar de antes. Aún así, a pesar de su similitud, ésta siempre ha sido la más difícil para mí. Todo parece pospuesto, y hay que recordar en qué orden hacerlo después.
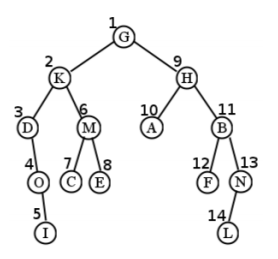
Para nuestro árbol de muestra, el primer nodo visitado resulta ser I. Esto se debe a que tenemos que posponer la visita a G hasta que terminemos su subárbol izquierdo (y derecho); luego posponemos K hasta que terminemos su subárbol izquierdo (y derecho); posponer D hasta que terminemos con el subárbol de O, y posponemos O hasta que hagamos I. Luego, finalmente, el la cosa comienza a relajarse... todo el camino de regreso a K. Pero en realidad no podemos visitar a la propia K todavía, porque tenemos que hacer su subárbol correcto. Esto da como resultado C, E y M, en ese orden. Entonces podemos hacer K, pero aún no podemos hacer G porque tenemos todo el mundo de su subárbol derecho con el que enfrentarnos. Todo el orden termina siendo: I, O, D, C, E, M, K, A, F, L, N, B, H, y finalmente G. (Ver Figura\(\PageIndex{11}\) para una visual.)
Tenga en cuenta que esto no es remotamente lo contrario de la visita de pre-orden, como es de esperar. G es último en lugar de primero, pero el resto está todo desordenado.
-
Tratar al niño izquierdo y a todos sus descendientes como un subárbol, y recorrerlo en su totalidad.
-
Visita la raíz.
-
Atraviesa el subárbol derecho en su totalidad.
Entonces, en lugar de visitar la raíz primero (pre-order) o last (post-order) la tratamos entre nuestros hijos izquierdo y derecho. Esto puede parecer algo extraño de hacer, pero hay un método para la locura que quedará claro en la siguiente sección.
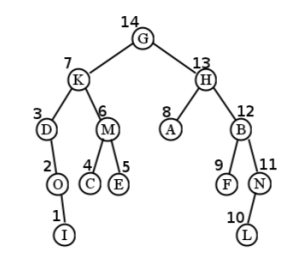
Para el árbol de muestra, el primer nodo visitado es D. Esto se debe a que es el primer nodo encontrado que no tiene un subárbol izquierdo, lo que significa que el paso 1 no necesita hacer nada. A esto le siguen O y yo, por la misma razón. Luego visitamos K antes de su subárbol derecho, que a su vez visita C, M y E, en ese orden. El orden final es: D, O, I, K, C, M, E, G, A, H, F, B, L, N. (Ver Figura\(\PageIndex{13}\).)
Si sus nodos están espaciados uniformemente, puede leer el recorrido en orden del diagrama moviendo los ojos de izquierda a derecha. Sin embargo, ten cuidado con esto porque en última instancia la posición espacial no importa, sino más bien las relaciones entre los nodos. Por ejemplo, si hubiera dibujado el nodo I más a la derecha, para hacer menos empinadas las líneas entre D—O—I, ese nodo I podría haber sido empujado físicamente a la derecha de K. Pero eso no cambiaría el orden y K lo había visitado antes.
Por último, cabe mencionar que todos estos métodos transversales hacen un uso elegante de la recursión. La recursión es una forma de tomar un problema grande y dividirlo en subproblemas similares, pero más pequeños. Entonces, cada uno de esos subproblemas puede ser atacado de la misma manera que atacaste al problema mayor: dividiéndolos en subproblemas. Todo lo que necesitas es una regla para eventualmente detener el proceso de “ruptura” haciendo algo realmente.
Cada vez que uno de estos procesos transversales trata a un hijo izquierdo o derecho como un subárbol, están “recurriendo” al reiniciar todo el proceso de recorrido en un árbol más pequeño. El recorrido por pre-orden, por ejemplo, después de visitar la raíz, dice: “bien, pretendamos que comenzamos todo este asunto del recorrido con el árbol más pequeño enraizado en mi hijo izquierdo. Una vez que eso haya terminado, despiértame para que pueda iniciarlo de manera similar con mi hijo adecuado”. La recursión es una forma muy común y útil de resolver ciertos problemas complejos, y los árboles están plagados de oportunidades.
Tamaños de árboles binarios
Los árboles binarios pueden ser de cualquier forma vieja irregular, como nuestro\(\PageIndex{10}\) ejemplo de Figura. A veces, sin embargo, queremos hablar de árboles binarios con una forma más regular, que satisfacen ciertas condiciones. En particular, hablaremos de tres tipos especiales:
árbol binario completo.
Un árbol binario completo es aquel en el que cada nodo (excepto las hojas) tiene dos hijos. Dicho de otra manera, cada nodo tiene dos hijos o ninguno: no se permite el rigor. La figura no\(\PageIndex{10}\) está llena, pero lo sería si agregáramos los tres nodos en blanco en la Figura\(\PageIndex{14}\).
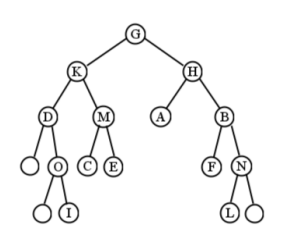
Por cierto, no siempre es posible tener un árbol binario completo con un número particular de nodos. Por ejemplo, un árbol binario con dos nodos, no puede estar lleno, ya que inevitablemente tendrá una raíz con un solo hijo.
árbol binario completo.
Un árbol binario completo es aquel en el que cada nivel tiene todos los nodos posibles presentes, excepto quizás el nivel más profundo, que se llena todo el camino desde la izquierda. La figura no\(\PageIndex{14}\) está llena, pero lo sería si la arregláramos como en la Figura\(\PageIndex{15}\).
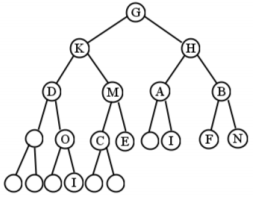
A diferencia de los árboles binarios completos, siempre es posible tener un árbol binario completo sin importar cuántos nodos contenga. Simplemente sigues rellenando de izquierda a derecha, nivel tras nivel.
árbol binario perfecto.
Nuestro último tipo especial tiene un título bastante audaz, pero un árbol “perfecto” es simplemente uno que está exactamente equilibrado: cada nivel está completamente lleno. La figura no\(\PageIndex{15}\) es perfecta, pero sería si agregáramos nodos para llenar el nivel 4, o eliminamos la parte inconclusa del nivel 3 (como en la Figura)\(\PageIndex{16}\).
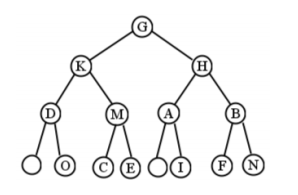
Los árboles binarios perfectos obviamente tienen las restricciones de tamaño más estrictas. Solo es posible, de hecho, tener árboles binarios perfectos con\(2^{h+1}-1\) nodos, si\(h\) es la altura del árbol. Entonces hay árboles binarios perfectos con 1, 3, 7, 15, 31,... nodos, pero ninguno en el medio. En cada uno de esos árboles,\(2^h\) de los nodos (casi exactamente la mitad) son hojas.
Ahora como veremos, los árboles binarios pueden poseer algunos poderes bastante sorprendentes si los nodos dentro de ellos están organizados de ciertas maneras. Específicamente, un árbol de búsqueda binaria y un montón son dos tipos especiales de árboles binarios que se ajustan a restricciones específicas. En ambos casos, lo que los hace tan poderosos es la velocidad a la que un árbol crece a medida que se le agregan nodos.
Supongamos que tenemos un árbol binario perfecto. Para hacerlo concreto, digamos que tiene altura 3, lo que le daría 1+2+4+8=15 nodos, 8 de los cuales son hojas. Ahora, ¿qué pasa si aumentas la altura de este árbol a 4? Si todavía es un árbol “perfecto”, habrás agregado 16 nodos más (todas las hojas). Así se ha duplicado el número de hojas simplemente agregando un nivel más. Esto cae en cascada cuantos más niveles agregues. Un árbol de altura 5 vuelve a duplicar el número de hojas (a 32), y la altura 6 lo vuelve a duplicar (a 64).
Si esto no te parece increíble, probablemente sea porque no aprecias completamente lo rápido que puede acumularse este tipo de crecimiento exponencial. Supongamos que tenías un árbol binario perfecto de altura 30, ciertamente no una figura impresionante. Uno podría imaginarlo encajando en una hoja de papel... en cuanto a la altura, es decir. Pero corre los números y descubrirás que tal árbol habría terminado, más de uno por cada persona en Estados Unidos. Aumenta la altura del árbol a solo 34 —solo 4 niveles adicionales— y de repente tienes más de 8 mil millones de hojas, fácilmente mayores que la población del planeta Tierra.
El poder de crecimiento exponencial sólo se alcanza plenamente cuando el árbol binario es perfecto, ya que un árbol con algunos nodos internos “faltantes” no lleva la capacidad máxima de la que es capaz. Tiene algunos agujeros en él. Aún así, mientras el árbol sea bastante tupido (es decir, no está horriblemente desequilibrado en solo unas pocas áreas) el enorme crecimiento pronosticado para árboles perfectos sigue siendo aproximadamente el caso.
La razón por la que esto se llama crecimiento “exponencial” es que la cantidad que estamos variando —la altura— aparece como exponente en el número de hojas, que es\(2^h\). Cada vez que añadimos un solo nivel, duplicamos el número de hojas.
Entonces el número de hojas (llámalo\(l\)) es\(2^h\), si\(h\) es la altura del árbol. Volteando esto, decimos eso\(h = \lg(l)\). La función “lg” es un logaritmo, específicamente un logaritmo con base-2. Esto es lo que suelen utilizar los informáticos, en lugar de una base de 10 (que se escribe “log”) o una base de\(e\) (que se escribe “ln”). Ya que\(2^h\) crece muy, muy rápido, se deduce que\(\lg(l)\) crece muy, muy lentamente. Después de que nuestro árbol alcance algunos millones de nodos, podemos agregar más y más nodos sin crecer la altura del árbol significativamente en absoluto.
El mensaje para llevar aquí es simplemente que una cantidad increíblemente grande de nodos se pueden acomodar en un árbol con una altura muy modesta. Esto permite, entre otras cosas, buscar una gran cantidad de información asombrosamente rápidamente... siempre que el contenido del árbol esté organizado correctamente.
Árboles de búsqueda binaria (BST's)
Bien, entonces hablemos de cómo organizar esos contenidos. Un árbol de búsqueda binaria (BST) es cualquier árbol binario que satisface una propiedad adicional: cada nodo es “mayor que” todos los nodos en su subárbol izquierdo, y “menor que (o igual a)” todos los nodos en su subárbol derecho. Llamaremos a esto la propiedad BST. Las frases “mayor que” y “menor que” están entre comillas aquí porque su significado es algo flexible, dependiendo de lo que estemos almacenando en el árbol. Si estamos almacenando números, usaremos orden numérico. Si estamos almacenando nombres, usaremos orden alfabético. Sea lo que sea que estemos almacenando, simplemente necesitamos una forma de comparar dos nodos para determinar cuál “va antes” al otro.
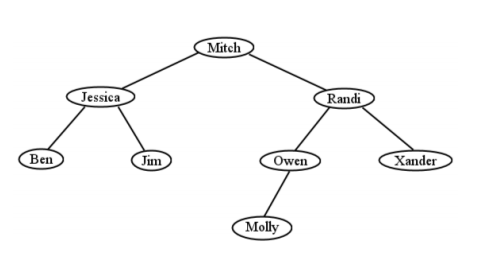
Un ejemplo de un BST que contiene personas se da en la Figura\(\PageIndex{17}\). Imagina que cada uno de estos nodos contiene una buena cantidad de información sobre una persona en particular: un registro de empleado, historial médico, información de cuenta, qué tienes. Los nodos en sí están indexados por el nombre de la persona, y los nodos se organizan de acuerdo con la regla BST. Mitch viene después de Ben/Jessica/Jim y antes de Randi/Owen/Molly/Xander en orden alfabético, y esta relación ordenadora entre padres e hijos se repite hasta el final del árbol. (¡Compruébalo!)
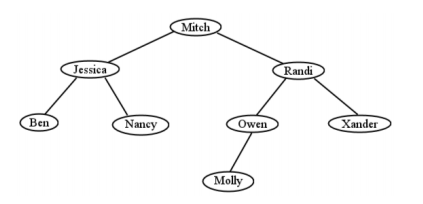
Tenga cuidado de observar que la regla de ordenación se aplica entre un nodo y todo el contenido de sus subárboles, no meramente a sus hijos inmediatos. Este es un error de novato que quieres evitar. Tu primera inclincación, al mirar la Figura\(\PageIndex{18}\), a continuación, es juzgarla como un BST. ¡No es un árbol de búsqueda binaria, sin embargo! Jessica está a la izquierda de Mitch, como debería estar, y Nancy está a la derecha de Jessica, como debería estar. Parece que se echa un vistazo. Pero el problema es que Nancy es descendiente del subárbol izquierdo de Mitch, mientras que ella debe colocarse adecuadamente en algún lugar de su subárbol derecho. Y sí, esto importa. Así que asegúrate de revisar tus BST todo el camino hacia arriba y hacia abajo.
El poder de los BST
Bien, entonces, ¿qué hay de los BST, de todos modos? El insight clave es darte cuenta de que si buscas un nodo, todo lo que tienes que hacer es comenzar por la raíz e ir la altura del árbol hacia abajo haciendo una comparación en cada nivel. Digamos que estamos buscando Figura\(\PageIndex{17}\) para Molly. Al mirar a Mitch (la raíz), sabemos de inmediato que Molly debe estar en el subárbol derecho, no en el izquierdo, porque viene tras Mitch en orden alfabético. Entonces miramos a Randi. Esta vez, nos encontramos con que Molly viene antes que Randi, por lo que debe estar en algún lugar de la rama izquierda de Randi. Owen nos manda otra vez a la izquierda, momento en el que encontramos a Molly.
Con un árbol de este tamaño, no parece tan asombroso. Pero supongamos que su altura era de 10. Esto significaría alrededor de 2000 nodos en el árbol: clientes, usuarios, amigos, lo que sea. Con un BST, solo tendrías que examinar diez de esos 2000 nodos para encontrar lo que estés buscando, mientras que si los nodos estuvieran solo en una lista ordinaria, tendrías que compararlos con 1000 más o menos de ellos antes de tropezar con el que estabas buscando. Y a medida que crece el tamaño del árbol, esta discrepancia crece (mucho) más grande. Si quisieras encontrar los registros de una sola persona en la ciudad de Nueva York, ¿preferirías buscar 7 millones de nombres, o 24 nombres? Porque esa es la diferencia que estás viendo.
Parece casi demasiado bueno para ser verdad. ¿Cómo es posible tal velocidad? El truco es darse cuenta de que con cada nodo que miras, efectivamente eliminas la mitad del árbol restante de la consideración. Por ejemplo, si estamos buscando a Molly, podemos hacer caso omiso de toda la mitad izquierda de Mitch sin siquiera mirarla, entonces lo mismo para toda la mitad derecha de Randi. Si descartas la mitad de algo, luego la mitad de la mitad restante, luego la mitad otra vez, no te lleva mucho tiempo eliminar casi todas las pistas falsas.
Hay una manera formal de describir esta aceleración, llamada “notación Big-O”. Las sutilezas son un poco complejas, pero la idea básica es ésta. Cuando decimos que un algoritmo es “O (n)” (pronunciado “oh—of—n”), significa que el tiempo que lleva ejecutar el algoritmo es proporcional al número de nodos. Esto no implica ningún número específico de milisegundos ni nada, eso depende en gran medida del tipo de hardware de computadora, que tenga, el lenguaje de programación y una miríada de otras cosas. Pero lo que podemos decir de un algoritmo O (n) es que si duplicas el número de nodos, vas a duplicar aproximadamente el tiempo de ejecución. Si cuádruples el número de nodos, vas a cuadruplicar el tiempo de ejecución. Esto es lo que esperarías.
Buscar “Molly” en una simple lista sin clasificar de nombres es un prospecto O (n). Si hay mil nodos en la lista, en promedio encontrarás a Molly después de escanear a través de 500 de ellos. (Podrías tener suerte y encontrar a Molly al principio, pero entonces por supuesto podrías tener mucha mala suerte y no encontrarla hasta el final. Esto promedia aproximadamente la mitad del tamaño de la lista en el caso normal.) Si hay un millón de nodos, sin embargo, te llevará 500.000 travesías en promedio antes de encontrar a Molly. Diez veces más nodos significa diez veces más tiempo para encontrar a Molly, y mil veces más significa mil veces más tiempo. Bummer.
Buscar a Molly en un BST, sin embargo, es un proceso O (lg n). Recordemos que “lg” significa el logaritmo (base-2). Esto significa que duplicar el número de nodos le da un aumento minúsculo en el tiempo de ejecución. Supongamos que había mil nodos en tu árbol, como arriba. No tendrías que mirar a través de 500 para encontrar a Molly: solo tendrías que mirar a través de diez (porque\(\lg(1000) \approx 10\)). Ahora aumentarlo a un millón de nodos. No tendrías que mirar a través de 500.000 para encontrar a Molly: solo tendrías que mirar a través de veinte. Supongamos que tenías 6 mil millones de nodos en tu árbol (aproximadamente la población de la tierra). No tendrías que mirar a través de 3 mil millones de nodos: solo tendrías que mirar a través de treinta y tres. Absolutamente alucinante.
Adición de nodos a un BST
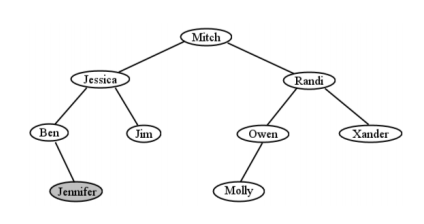
Encontrar cosas en un BST es rápido como un rayo. Resulta, así es agregarle cosas. Supongamos que adquirimos un nuevo cliente llamado Jennifer, y necesitamos agregarla a nuestro BST para que podamos recuperar la información de su cuenta en el futuro. Todo lo que hacemos es seguir el mismo proceso que haríamos si estuviéramos buscando a Jennifer, pero en cuanto encontremos el lugar donde estaría, la agregamos ahí. En este caso, Jennifer viene antes que Mitch (vaya a la izquierda), y antes Jessica (vuelva a la izquierda), y después de Ben (vaya a la derecha). Ben no tiene un hijo adecuado, así que pusimos a Jessica en el árbol justo en ese momento. (Ver Figura\(\PageIndex{19}\).)
Este proceso de adición también es un algoritmo O (lg n), ya que solo necesitamos mirar un pequeño número de nodos igual a la altura del árbol.
Tenga en cuenta que una nueva entrada siempre se convierte en una hoja cuando se agrega. De hecho, esto nos permite mirar al árbol y reconstruir algo de lo que vino antes. Por ejemplo, sabemos que Mitch debió haber sido el primer nodo originalmente insertado, y que Randi se insertó antes que Owen, Xander o Molly. Como ejercicio, agrega tu propio nombre a este árbol (y algunos de los nombres de tus amigos) para asegurarte de que lo aprendas. Cuando hayas terminado, el árbol debe obedecer por supuesto la propiedad BST.
Eliminación de nodos de un BST
Eliminar nodos es un poco más complicado que agregarlos. ¿Cómo eliminamos una entrada sin estropear la estructura del árbol? Es fácil ver cómo eliminar a Molly: ya que ella es solo una hoja, solo quítala y termina con ella. Pero, ¿cómo eliminar a Jessica? ¿O para el caso, Mitch?
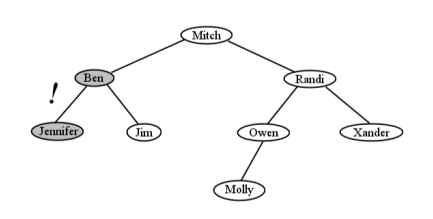
Tu primera inclinación podría ser eliminar un nodo y promover que uno de sus hijos suba en su lugar. Por ejemplo, si eliminamos a Jessica, podríamos simplemente elevar a Ben hasta donde estaba Jessica, y luego mover a Jennifer por debajo de Ben también. Esto no funciona, sin embargo. El resultado se vería como Figura\(\PageIndex{20}\), con Jennifer en el lugar equivocado. La próxima vez que busquemos a Jennifer en el árbol, buscaremos a la derecha de Ben (como deberíamos), extrañándola por completo. Jennifer efectivamente se ha perdido.
Una forma correcta (hay otras) de hacer una eliminación de nodo es reemplazar el nodo con el descendiente más a la izquierda de su subárbol derecho. (O, equivalentemente, el descendiente más a la derecha de su subárbol izquierdo). En la figura se\(\PageIndex{21}\) muestra el resultado después de retirar a Jessica. La reemplazamos por Jim, no porque esté bien promover ciegamente al hijo adecuado, sino porque Jim no tenía descendientes izquierdos. Si lo hubiera hecho, promocionarlo hubiera sido tan erróneo como promocionar a Ben. En cambio, habríamos promovido al descendiente más a la izquierda de Jim.
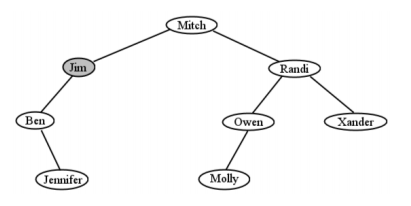
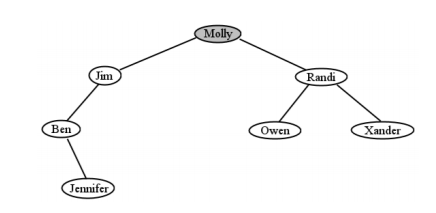
Como otro ejemplo, vayamos whole-hog y eliminemos el nodo raíz, Mitch. El resultado es como se muestra en la Figura\(\PageIndex{22}\). Es de harapa-a-riquezas para Molly: fue ascendida de una hoja hasta la cima. ¿Por qué Molly? Porque era la descendiente más a la izquierda del subárbol derecho de Mitch.
Para ver por qué funciona esto, solo considera que Molly fue inmediatamente después de Mitch en orden alfabético. El hecho de que él fuera un rey y ella campesina era engañosa. Los dos estaban en realidad muy cerca: consecutivos, de hecho, con recorrido en orden. Así que reemplazar Mitch por Molly evita barajar a nadie fuera de orden alfabético, y conserva la importantísima propiedad BST.
Equilibramiento
Por último, recordemos que esta búsqueda increíblemente rápida depende críticamente de que el árbol sea “tupido”. De lo contrario, la aproximación que\(h=\lg(l)\) se descompone. Como ejemplo ridículamente extremo, considera Figure\(\PageIndex{23}\), que contiene los mismos nodos que hemos estado usando. ¡Este es un árbol de búsqueda binario legítimo! (¡Compruébalo!) Sin embargo, buscar un nodo en esta monstruosidad obviamente no va a ser más rápido que buscarlo en una lista sencilla y antigua. Volvemos a O (n) performance.
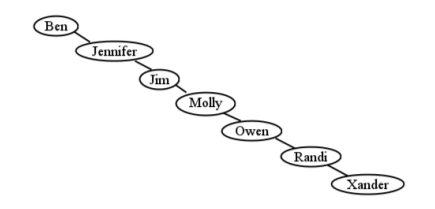
En la práctica, hay tres formas de lidiar con esto. Un enfoque es simplemente no preocuparse por ello. Después de todo, siempre y cuando estemos insertando y eliminando nodos aleatoriamente, sin un patrón discernible, las posibilidades de obtener un árbol tan desigual como la Figura\(\PageIndex{23}\) son astronómicamente pequeñas. Es tan probable como lanzar una baraja de cartas al aire y tenerla aterrizar todo en una pila ordenada. La ley de la entropía nos dice que vamos a obtener una mezcla de ramas cortas y ramas largas, y que en un árbol grande, el desequilibrio será mínimo.
Un segundo enfoque es reequilibrar periódicamente el árbol. Si nuestro sitio web se desconecta para mantenimiento de vez en cuando de todos modos, podríamos reconstruir nuestro árbol desde cero insertando los nodos en un árbol fresco en un orden beneficioso. ¿En qué orden debemos insertarlos? Bueno, recuerda que cualquiera que sea el nodo que se inserte primero será la raíz. Esto sugiere que querríamos insertar primero el nodo central en nuestro árbol, para que Molly se convierta en la nueva raíz. Esto deja la mitad de los nodos para su subárbol izquierdo y la mitad para su derecha. Si sigues este proceso de manera lógica (y recursiva) te darás cuenta de que a continuación queremos insertar los nodos medios de cada mitad. Esto equivaldría a Jennifer y Randi (en cualquier orden). Pienso en ello como las marcas en una regla: primero se inserta media pulgada, luego\(\frac{1}{4}\) y\(\frac{3}{4}\) pulgadas, luego\(\frac{1}{8}\)\(\frac{3}{8}\),\(\frac{5}{8}\),, y\(\frac{7}{8}\) pulgadas, etc. esto nos restaura una perfección árbol equilibrado a intervalos regulares, haciendo que cualquier desequilibrio grande sea aún más improbable (y de corta duración).
En tercer lugar, hay estructuras de datos especializadas que puede conocer en cursos futuros, como árboles AVL y árboles rojo-negros, que son árboles de búsqueda binarios que agregan reglas adicionales para evitar desequilibrios. Básicamente, la idea es que cuando se inserta (o elimina) un nodo, se comprueban ciertas métricas para asegurarse de que el cambio no causó un desequilibrio demasiado grande. Si lo hizo, el árbol se ajusta para minimizar el desequilibrio. Esto tiene un ligero costo cada vez que se cambia el árbol, pero evita cualquier posibilidad de un árbol desequilibrado que provoque búsquedas lentas a la larga.
- No parece haber consenso en cuanto a cuál de estos conceptos es el más básico. Algunos autores se refieren a un árbol libre simplemente como un “árbol” —como si este fuera el tipo de árbol “normal ”— y utilizan el término árbol enraizado para el otro tipo. Otros autores hacen lo contrario. Para evitar confusiones, intentaré usar siempre el término completo (aunque admito que soy de los que considera que los árboles enraizados son el concepto más importante, por defecto).