17: Flujo más allá de un obstáculo
- Page ID
- 117260
Consideramos ahora un problema clásico en la dinámica de fluidos computacional: el flujo estable y bidimensional más allá de un obstáculo. Aquí, consideramos flujos más allá de un rectángulo y un círculo.
Primero, consideramos flujo más allá de un rectángulo. El sistema simple de coordenadas cartisianas es el más adecuado para este problema, y los límites del rectángulo interno pueden alinearse con la cuadrícula computacional. Segundo, consideramos fluir más allá de un círculo. Aquí, el sistema de coordenadas polares es el más adecuado, y esto introduce algunas complicaciones analíticas adicionales a la formulación del problema. Sin embargo, veremos que el cálculo del flujo más allá de un círculo puede ser de hecho más simple que el flujo pasado un rectángulo. Aunque el flujo más allá de un rectángulo contiene dos parámetros adimensionales, el flujo más allá de un círculo contiene solo uno. Además, el flujo más allá de un círculo puede resolverse dentro de un dominio rectangular que no tiene límites internos.
Flujo más allá de un rectángulo
La velocidad de la corriente libre viene dada por\(\mathbf{u}=U \hat{\mathbf{x}}\) y se supone que el obstáculo rectangular tiene anchura\(W\) y altura\(H\). Ahora, la función de corriente tiene unidades de velocidad por longitud, y la vorticidad tiene unidades de velocidad divididas por longitud. Las ecuaciones de Poisson bidimensionales estables para la función de arroyo y la vorticidad, dadas por (16.14) y (16.18), pueden ser no dimensionalizadas usando la velocidad\(U\) y la longitud\(W\). Las ecuaciones adimensionales resultantes se pueden escribir como
\[\begin{align} &-\nabla^{2} \psi=\omega, \\ &-\nabla^{2} \omega=\operatorname{Re}\left(\frac{\partial \psi}{\partial x} \frac{\partial \omega}{\partial y}-\frac{\partial \psi}{\partial y} \frac{\partial \omega}{\partial x}\right), \end{align} \nonumber \]
donde el parámetro adimensional Re se llama el número de Reynolds. Un parámetro adimensional adicional surge de la relación de aspecto del obstáculo rectangular, y se denota por\(a\). Estos dos parámetros adimensionales están definidos por
\[\operatorname{Re}=\frac{U W}{V}, \quad a=\frac{W}{H} . \nonumber \]
Se buscará una solución para la función de flujo escalar y el campo de vorticidad escalar para diferentes valores del número de Reynolds Re en una relación de aspecto fija\(a\)
Aproximación de diferencia finita
Construimos una cuadrícula rectangular para una solución numérica. Haremos uso de celdas de cuadrícula cuadrada, y escribiremos
\[\begin{array}{ll} x_{i}=i h, & i=0,1, \ldots, N_{x} ; \\ y_{j}=j h, & j=0,1, \ldots, N_{y}, \end{array} \nonumber \]
donde\(N_{x}\) y\(N_{y}\) son el número de celdas de cuadrícula que abarcan las\(y\) direcciones\(x\) - y -y\(h\) es la longitud lateral de una celda de cuadrícula.
Para obtener una solución precisa, requerimos que los límites del obstáculo se encuentren exactamente en los límites de la celda de la cuadrícula. El ancho del obstáculo en nuestra formulación adimensional es la unidad, y colocamos el frente del obstáculo en\(x=m h\) y la parte posterior del obstáculo en\(x=(m+I) h\), donde debemos tener
\[h I=1 \text {. } \nonumber \]
Con\(I\) especificado, el espaciado de rejilla está determinado por\(h=1 / I\).
Solo buscaremos soluciones estables para el campo de flujo que sean simétricas alrededor de la línea media del obstáculo. Asumiendo simetría, solo necesitamos resolver para el campo de flujo en la mitad superior del dominio. Colocamos la línea central del obstáculo en\(y=0\) y la parte superior del rectángulo en\(h J .\) La media altura adimensional del obstáculo viene dada por\(1 / 2 a\), de modo que
\[h J=\frac{1}{2 a} . \nonumber \]
Forzar el rectángulo a acostarse sobre las líneas de la cuadrícula limita la elección de la relación de aspecto y los valores de\(I\) y\(J\) tal que
\[a=\frac{I}{2 J} \text {. } \nonumber \]
Los valores razonables de\(a\) a considerar son\(a=\ldots, 1 / 4,1 / 2,1,2,4, \ldots\), etc,\(I\) y se\(J\) pueden ajustar en consecuencia.
La física del problema se especifica a través de los dos parámetros adimensionales Re y\(a\). Los números del problema se especifican por los parámetros\(N_{x}, N_{y}, h\), y la colocación del rectángulo en el dominio computacional. Buscamos la convergencia de la solución numérica como\(h \rightarrow 0, N_{x}, N_{y} \rightarrow \infty\) y el rectángulo se coloca lejos de los límites del dominio computacionalmente.
Discretizando las ecuaciones gobernantes, ahora escribimos
\[\psi_{i, j}=\psi\left(x_{i}, y_{j}\right), \quad \omega_{i, j}=\omega\left(x_{i}, y_{j}\right) . \nonumber \]
Para resolver las ecuaciones acopladas de Poisson dadas por (17.1) y (17.2), se hace uso del método SOR, descrito anteriormente en §7.1. La notación que usamos aquí es para el método Jacobi, pero es probable que se logre una convergencia más rápida usando el dorso rojo Gauss-Seidel. La ecuación de Poisson para la función stream, dada por (17.1), se convierte en
\[\psi_{i, j}^{n+1}=\left(1-r_{\psi}\right) \psi_{i, j}^{n}+\frac{r_{\psi}}{4}\left(\psi_{i+1, j}^{n}+\psi_{i-1, j}^{n}+\psi_{i, j+1}^{n}+\psi_{i, j-1}^{n}+h^{2} \omega_{i, j}^{n}\right) . \nonumber \]
La ecuación de Poisson para la vorticidad, dada por\((17.2)\), requiere el uso de la aproximación de diferencia finita centrada para las derivadas que aparecen en el lado derecho. Para\(x=x_{i}, y=y_{i}\), estas aproximaciones vienen dadas por
\[\begin{array}{ll} \frac{\partial \psi}{\partial x} \approx \frac{1}{2 h}\left(\psi_{i+1, j}-\psi_{i-1, j}\right), & \frac{\partial \psi}{\partial y} \approx \frac{1}{2 h}\left(\psi_{i, j+1}-\psi_{i, j-1}\right) \\ \frac{\partial \omega}{\partial x} \approx \frac{1}{2 h}\left(\omega_{i+1, j}-\omega_{i-1, j}\right), & \frac{\partial \omega}{\partial y} \approx \frac{1}{2 h}\left(\omega_{i, j+1}-\omega_{i, j-1}\right) . \end{array} \nonumber \]
Luego escribimos para (17.2),
\[\omega_{i, j}^{n+1}=\left(1-r_{\omega}\right) \omega_{i, j}^{n}+\frac{r_{\omega}}{4}\left(\omega_{i+1, j}^{n}+\omega_{i-1, j}^{n}+\omega_{i, j+1}^{n}+\omega_{i, j-1}^{n}+\frac{\operatorname{Re}}{4} f_{i, j}^{n}\right), \nonumber \]
donde
\[f_{i j}^{n}=\left(\psi_{i+1, j}^{n}-\psi_{i-1, j}^{n}\right)\left(\omega_{i, j+1}^{n}-\omega_{i, j-1}^{n}\right)-\left(\psi_{i, j+1}^{n}-\psi_{i, j-1}^{n}\right)\left(\omega_{i+1, j}^{n}-\omega_{i-1, j}^{n}\right) \nonumber \]
Ahora, el lado derecho de (17.11) contiene un término no lineal dado por (17.12). Esta no linealidad puede resultar en que las iteraciones se vuelvan inestables.
Las iteraciones se pueden estabilizar de la siguiente manera. Primero, los parámetros de relajación,\(r_{\psi}\) y\(r_{\omega}\), deben ser menores o iguales a la unidad, y las iteraciones inestables a menudo se pueden hacer estables disminuyendo\(r_{\omega}\). Se necesita experimentar numéricamente para obtener el mejor equilibrio entre estabilidad computacional y velocidad. Segundo, para determinar la solución con el número de Reynolds Re, la iteración debe inicializarse usando la solución estable para un número de Reynolds ligeramente menor. Se deben elegir las condiciones iniciales para la primera solución con Re ligeramente mayor que cero para que esta primera iteración sea estable.
La ruta de convergencia se puede rastrear durante las iteraciones. Definimos
\[\begin{aligned} &\varepsilon_{\psi}^{n+1}=\max _{i, j}\left|\psi_{i, j}^{n+1}-\psi_{i, j}^{n}\right| \\ &\varepsilon_{\omega}^{n+1}=\max _{i, j}\left|\omega_{i, j}^{n+1}-\omega_{i, j}^{n}\right| . \end{aligned} \nonumber \]
Las iteraciones deben detenerse cuando los valores de\(\varepsilon_{\psi}^{n+1}\) y\(\varepsilon_{\omega}^{n+1}\) son menores que alguna tolerancia de error predefinida, digamos\(10^{-8}\).
Condiciones de contorno
Condiciones de límite sobre\(\psi_{i, j}\) y\(\omega_{i, j}\) deben prescribirse en\(i=0\) (entrada),\(i=N_{x}\) (salida),\(j=0\) (línea media) y\(j=N_{y}\) (parte superior del dominio computacional). Además, se deben prescribir condiciones de límite en la superficie del obstáculo; es decir, en la superficie frontal:\(i=m, 0 \leq j \leq I\); la superficie posterior:\(i=m+I, 0 \leq j \leq J\); y la superficie superior:\(m \leq i \leq m+I, j=J .\) Dentro del obstáculo\(m<i<m+I, 0<j<J\), no se busca ninguna solución.
Para las condiciones de límite de entrada y de nivel superior de dominio, podemos suponer que el campo de flujo satisface condiciones de flujo libre adimensional; es decir,
\[u=1, \quad v=0 . \nonumber \]
La vorticidad se puede tomar como cero, y la función de corriente satisface
\[\frac{\partial \psi}{\partial y}=1, \quad \frac{\partial \psi}{\partial x}=0 \nonumber \]
Integrando la primera de estas ecuaciones, obtenemos
\[\psi=y+f(x) ; \nonumber \]
y a partir de la segunda ecuación que obtenemos\(f(x)=c\), donde\(c\) es una constante. Sin pérdida de generalidad, podemos elegir\(c=0\). Por lo tanto, para las condiciones de entrada y límite superior de dominio, tenemos
\[\psi=y, \quad \omega=0 \nonumber \]
En la parte superior del dominio, observe que\(y=N_{y} h\) es una constante.
Para las condiciones de límite de salida, tenemos dos opciones posibles. Podríamos asumir condiciones de transmisión libre si colocamos el límite de salida lo suficientemente lejos del obstáculo. Sin embargo, cabría esperar que la perturbación en el campo de flujo aguas abajo del obstáculo pudiera ser sustancialmente mayor que la corriente arriba del obstáculo. Quizás mejores condiciones de límite de flujo de salida pueden ser cero derivadas normales del campo de flujo; es decir
\[\frac{\partial \psi}{\partial x}=0, \quad \frac{\partial \omega}{\partial x}=0 \nonumber \]
Para las condiciones de contorno de la línea media, asumiremos un campo de flujo simétrico para que el patrón de flujo se vea igual cuando se rote alrededor del\(x\) eje. Por tanto, las condiciones de simetría están dadas por
\[u(x,-y)=u(x, y), \quad v(x,-y)=-v(x, y) . \nonumber \]
La vorticidad exhibe la simetría dada por
\[\begin{aligned} \omega(x,-y) &=\frac{\partial v(x,-y)}{\partial x}-\frac{\partial u(x,-y)}{\partial(-y)} \\ &=-\frac{\partial v(x, y)}{\partial x}+\frac{\partial u(x, y)}{\partial(y)} \\ &=-\omega(x, y) \end{aligned} \nonumber \]
En la línea media\((y=0)\), entonces,\(\omega(x, 0)=0 .\) También,\(v(x, 0)=0 .\) Con\(v=-\partial \psi / \partial x\), debemos tener\(\psi(x, 0)\) independiente de\(x\), o\(\psi(x, 0)\) igual a una constante. La coincidencia de la condición de límite de línea media con nuestra condición de entrada elegida determina\(\psi(x, 0)=0\).
Nuestras condiciones de límite son discretizadas usando (17.4). La condición de salida de la derivada normal cero podría aproximarse a primer o segundo orden. Dado que es una condición de límite aproximada, el primer orden es probablemente suficiente y usamos\(\psi_{N_{x}, j}=\psi_{N_{x}-1, j}\) y\(\omega_{N_{x}, j}=\)\(\omega_{N_{x}-1, j} .\)
Al juntar todos estos resultados, las condiciones límite en los bordes del dominio computacional están dadas por
\[\begin{aligned} \psi_{i, 0} &=0, & \omega_{i, 0} &=0, & \text { midline; } \\ \psi_{0, j} &=j h, & \omega_{0, j} &=0, & \text { inflow; } \\ \psi_{N_{x}, j} &=\psi_{N_{x}-1, j,} & \omega_{N_{x}, j} &=\omega_{N_{x}-1, j \prime} & \text { outflow; } \\ \psi_{i, N_{y}} &=N_{y} h, & \omega_{i, N_{y}} &=0, & \text { top-of-domain. } \end{aligned} \nonumber \]
Las condiciones de límite en el obstáculo se pueden derivar de las condiciones de no penetración y de deslizamiento. Desde la condición de no penetración,\(u=0\) en los lados y\(v=0\) en la parte superior. Por lo tanto, en los lados\(\partial \psi / \partial y=0\), y dado que los límites laterales son paralelos al\(y\) eje -eje,\(\psi\) deben ser constantes. En la parte superior,\(\partial \psi / \partial x=0\), y dado que la parte superior es paralela al\(x\) eje -eje,\(\psi\) debe ser constante. Coincidiendo la constante con el valor de\(\psi\) en la línea media, obtenemos\(\psi=0\) a lo largo del límite del obstáculo.
Desde la condición antideslizante,\(v=0\) en los lados y\(u=0\) en la parte superior. Por lo tanto,\(\partial \psi / \partial x=0\) en los lados y\(\partial \psi / \partial y=0\) en la parte superior. Para interpretar las condiciones de contorno antideslizamiento en términos de condiciones de límite sobre la vorticidad, hacemos uso de\((17.1)\); es decir,
\[\omega=-\left(\frac{\partial^{2} \psi}{\partial x^{2}}+\frac{\partial^{2} \psi}{\partial y^{2}}\right) \nonumber \]
Primero consideremos los lados del obstáculo. Ya que\(\psi\) es independiente de\(y\) lo que tenemos\(\partial^{2} \psi / \partial y^{2}=0\), y (17.19) se convierte
\[\omega=-\frac{\partial^{2} \psi}{\partial x^{2}} \nonumber \]
Ahora la serie Taylor expandimos\(\psi\left(x_{m}-h, y_{j}\right)\) y\(\psi\left(x_{m}-2 h, y_{j}\right)\) sobre\(\left(x_{m}, y_{j}\right)\), correspondiente a la cara frontal del obstáculo rectangular. Tenemos que ordenar\(h^{3}\):
\[\begin{aligned} &\psi_{m-1, j}=\psi_{m, j}-\left.h \frac{\partial \psi}{\partial x}\right|_{m, j}+\left.\frac{1}{2} h^{2} \frac{\partial^{2} \psi}{\partial x^{2}}\right|_{m, j}-\left.\frac{1}{6} h^{3} \frac{\partial^{3} \psi}{\partial x^{3}}\right|_{m, j}+\mathrm{O}\left(h^{4}\right), \\ &\psi_{m-2, j}=\psi_{m, j}-\left.2 h \frac{\partial \psi}{\partial x}\right|_{m, j}+\left.2 h^{2} \frac{\partial^{2} \psi}{\partial x^{2}}\right|_{m, j}-\left.\frac{4}{3} h^{3} \frac{\partial^{3} \psi}{\partial x^{3}}\right|_{m, j}+\mathrm{O}\left(h^{4}\right) . \end{aligned} \nonumber \]
Los primeros términos en las dos expansiones de la serie Taylor son cero debido a la condición de no penetración, y los segundos términos son cero debido a la condición de no deslizamiento. Los terceros términos pueden ser reescritos usando (17.20), y obtenemos
\[\begin{aligned} &\psi_{m-1, j}=-\frac{1}{2} h^{2} \omega_{m, j}-\left.\frac{1}{6} h^{3} \frac{\partial^{3} \psi}{\partial x^{3}}\right|_{m, j}+\mathrm{O}\left(h^{4}\right) \\ &\psi_{m-2, j}=-2 h^{2} \omega_{m, j}-\left.\frac{4}{3} h^{3} \frac{\partial^{3} \psi}{\partial x^{3}}\right|_{m, j}+\mathrm{O}\left(h^{4}\right) \end{aligned} \nonumber \]
Multiplicamos la primera ecuación por\(-8\) y la agregamos a la segunda ecuación para eliminar el\(h^{3}\) término. Obtenemos
\[-8 \psi_{m-1, j}+\psi_{m-2, j}=2 h^{2} \omega_{m, j}+\mathrm{O}\left(h^{4}\right) . \nonumber \]
Resolviendo la vorticidad, tenemos una condición de límite precisa de segundo orden dada por
\[\omega_{m, j}=\frac{\psi_{m-2, j}-8 \psi_{m-1, j}}{2 h^{2}} \nonumber \]
Consideraciones similares aplicadas a la cara posterior de los rendimientos de obstáculos rectangulares
\[\omega_{m+1, j}=\frac{\psi_{m+I+2, j}-8 \psi_{m+I+1, j}}{2 h^{2}} \nonumber \]
En la parte superior del obstáculo,\(y=J h\) se fija, y como\(\psi\) es independiente de\(x\), tenemos\(\partial^{2} \psi / \partial x^{2}=\) 0. Por lo tanto,
\[\omega=-\frac{\partial^{2} \psi}{\partial y^{2}} \nonumber \]
Ahora la serie Taylor expandimos\(\psi\left(x_{i}, y_{J+1}\right)\) y\(\psi\left(x_{i}, y_{J+2}\right)\) sobre\(\left(x_{i}, y_{J}\right) .\) Para ordenar\(h^{3}\),
\[\begin{aligned} &\psi_{i, J+1}=\psi_{i, J}+\left.h \frac{\partial \psi}{\partial y}\right|_{i, J}+\left.\frac{1}{2} h^{2} \frac{\partial^{2} \psi}{\partial y^{2}}\right|_{i, J}+\left.\frac{1}{6} h^{3} \frac{\partial^{3} \psi}{\partial y^{3}}\right|_{i, J}+\mathrm{O}\left(h^{4}\right), \\ &\psi_{i, J+2}=\psi_{i, J}+\left.2 h \frac{\partial \psi}{\partial y}\right|_{i, J}+\left.2 h^{2} \frac{\partial^{2} \psi}{\partial y^{2}}\right|_{i, J}+\left.\frac{4}{3} h^{3} \frac{\partial^{3} \psi}{\partial y^{3}}\right|_{i, J}+\mathrm{O}\left(h^{4}\right) . \end{aligned} \nonumber \]
Nuevamente, los términos primero y segundo en la expansión de la serie Taylor son cero, y haciendo uso de (17.24), obtenemos
\[\begin{aligned} &\psi_{i, J+1}=-\frac{1}{2} h^{2} \omega_{i, J}+\left.\frac{1}{6} h^{3} \frac{\partial^{3} \psi}{\partial y^{3}}\right|_{i, J}+\mathrm{O}\left(h^{4}\right), \\ &\psi_{i, J+2}=-2 h^{2} \omega_{i, J}+\left.\frac{4}{3} h^{3} \frac{\partial^{3} \psi}{\partial y^{3}}\right|_{i, J}+\mathrm{O}\left(h^{4}\right) . \end{aligned} \nonumber \]
Nuevamente, multiplicamos la primera ecuación por\(-8\) y la agregamos a la segunda ecuación para obtener
\[-8 \psi_{i, J+1}+\psi_{i, J+2}=2 h^{2} \omega_{i, J}+\mathrm{O}\left(h^{4}\right) \nonumber \]
Resolviendo la vorticidad en la superficie superior, tenemos que precisión de segundo orden
\[\omega_{i, J}=\frac{\psi_{i, J+2}-8 \psi_{i, J+1}}{2 h^{2}} \nonumber \]
Resumimos las condiciones de límite sobre el obstáculo:
\[\begin{array}{cc} \text { front face: } \psi_{m, j}=0, & \omega_{m, j}=\frac{\psi_{m-2, j}-8 \psi_{m-1, j}}{2 h^{2}}, \quad 0 \leq j \leq J ; \\ \text { back face: } \psi_{m+I, j}=0, & \omega_{m+I, j}=\frac{\psi_{m+I+2, j}-8 \psi_{m+I+1, j}}{2 h^{2}}, \quad 0 \leq j \leq J ; \\ \text { top face: } \psi_{i, J}=0, & \omega_{i, J}=\frac{\psi_{i, J+2}-8 \psi_{i, J+1}}{2 h^{2}}, \quad m \leq i \leq m+I . \end{array} \nonumber \]
Fluir más allá de un círculo
Ahora consideramos el flujo más allá de un obstáculo circular de radio\(R\), con velocidad de flujo libre\(\mathbf{u}=U \hat{\mathbf{x}}\) Aquí, no dimensionalizamos las ecuaciones gobernantes usando\(U\) y\(R\). Definiremos el número de Reynolds, el único parámetro adimensional de este problema, por
\[\operatorname{Re}=\frac{2 U R}{v} . \nonumber \]
El factor extra de 2 basa la definición del número de Reynolds en el diámetro del círculo más que en el radio, lo que permite una mejor comparación con los cálculos de flujo más allá de un cuadrado\((a=1)\), donde el número de Reynolds se basó en la longitud lateral
Las ecuaciones de gobierno adimensionales en forma vectorial, se pueden escribir como
\[\begin{align} \nonumber \nabla^{2} \psi &=-\omega \\ \nabla^{2} \omega &=\frac{\operatorname{Re}}{2} \mathbf{u} \cdot \nabla \omega \end{align} \nonumber \]
donde el factor extra de la mitad surge de no dimensionalizar la ecuación usando el radio del obstáculo\(R\), pero definiendo el número de Reynolds en términos del diámetro\(2 R\).
Coordenadas log-polares
Aunque la velocidad de flujo libre se expresa mejor en coordenadas cartesianas, los límites del obstáculo circular se expresan más simplemente en coordenadas polares, con origen en el centro del círculo. Las coordenadas polares se definen de la manera habitual por
\[x=r \cos \theta, \quad y=r \sin \theta, \nonumber \]
con los vectores unitarios cartesianos dados en términos de los vectores unitarios polares por
\[\hat{\mathbf{x}}=\cos \theta \hat{\mathbf{r}}-\sin \theta \hat{\boldsymbol{\theta}}, \quad \hat{\boldsymbol{y}}=\sin \theta \hat{\mathbf{r}}+\cos \theta \hat{\boldsymbol{\theta}} \nonumber \]
Los vectores de unidad polar son funciones de posición, y sus derivadas están dadas por
\[\frac{\partial \hat{\mathbf{r}}}{\partial r}=0, \quad \frac{\partial \hat{\mathbf{r}}}{\partial \theta}=\hat{\boldsymbol{\theta}}, \quad \frac{\partial \hat{\boldsymbol{\theta}}}{\partial r}=0, \quad \frac{\partial \hat{\boldsymbol{\theta}}}{\partial \theta}=-\hat{\mathbf{r}} \nonumber \]
El operador del diferencial en coordenadas polares viene dado por
\[\boldsymbol{\nabla}=\hat{\mathbf{r}} \frac{\partial}{\partial r}+\hat{\theta} \frac{1}{r} \frac{\partial}{\partial \theta} \nonumber \]
y el laplaciano bidimensional viene dado por
\[\nabla^{2}=\frac{1}{r^{2}}\left(\left(r \frac{\partial}{\partial r}\right)\left(r \frac{\partial}{\partial r}\right)+\frac{\partial^{2}}{\partial \theta^{2}}\right) \nonumber \]
El campo de velocidad se escribe en coordenadas polares como
\[\mathbf{u}=u_{r} \hat{\mathbf{r}}+u_{\theta} \hat{\theta} \nonumber \]
Se encuentra que la velocidad de flujo libre en coordenadas polares es
\[\begin{align} \nonumber \mathbf{u} &=U \hat{\mathbf{x}} \\ &=U(\cos \theta \hat{\mathbf{r}}-\sin \theta \hat{\boldsymbol{\theta}}), \end{align} \nonumber \]
de donde se pueden leer los componentes en coordenadas polares. La ecuación de continuidad\(\boldsymbol{\nabla} \cdot \mathbf{u}=\) 0 en coordenadas polares viene dada por
\[\frac{1}{r} \frac{\partial}{\partial r}\left(r u_{r}\right)+\frac{1}{r} \frac{\partial u_{\theta}}{\partial \theta}=0 \nonumber \]
para que la función stream pueda ser definida por
\[r u_{r}=\frac{\partial \psi}{\partial \theta}, \quad u_{\theta}=-\frac{\partial \psi}{\partial r} . \nonumber \]
La vorticidad, aquí en coordenadas cilíndricas, viene dada por
\[\begin{aligned} \omega &=\nabla \times \mathbf{u} \\ &=\hat{\mathbf{z}}\left(\frac{1}{r} \frac{\partial}{\partial r}\left(r u_{\theta}\right)-\frac{1}{r} \frac{\partial u_{r}}{\partial \theta}\right), \end{aligned} \nonumber \]
de modo que el componente z de la vorticidad para un flujo bidimensional viene dado por
\[\omega=\frac{1}{r} \frac{\partial}{\partial r}\left(r u_{\theta}\right)-\frac{1}{r} \frac{\partial u_{r}}{\partial \theta} . \nonumber \]
Además,
\[\begin{align} \nonumber \mathbf{u} \cdot \nabla &=\left(u_{r} \hat{\mathbf{r}}+u_{\theta} \hat{\boldsymbol{\theta}}\right) \cdot\left(\hat{\mathbf{r}} \frac{\partial}{\partial r}+\hat{\theta} \frac{1}{r} \frac{\partial}{\partial \theta}\right) \\ \nonumber &=u_{r} \frac{\partial}{\partial r}+\frac{u_{\theta}}{r} \frac{\partial}{\partial \theta} \\ &=\frac{1}{r} \frac{\partial \psi}{\partial \theta} \frac{\partial}{\partial r}-\frac{1}{r} \frac{\partial \psi}{\partial r} \frac{\partial}{\partial \theta} \end{align} \nonumber \]
Las ecuaciones gobernantes dadas por (17.29), entonces, con el laplaciano dado por (17.34), y el término de convección dado por (17.40), son
\[\begin{align} \nabla^{2} \psi &=-\omega \\ \nabla^{2} \omega &=\frac{\operatorname{Re}}{2}\left(\frac{1}{r} \frac{\partial \psi}{\partial \theta} \frac{\partial \omega}{\partial r}-\frac{1}{r} \frac{\partial \psi}{\partial r} \frac{\partial \omega}{\partial \theta}\right) \end{align} \nonumber \]
El factor recurrente\(r \partial / \partial r\) en la coordenada polar Laplaciana, (17.34), es incómodo de discretizar y buscamos un cambio de variables\(r=r(\xi)\), donde
\[r \frac{\partial}{\partial r}=\frac{\partial}{\partial \xi} . \nonumber \]
Ahora,
\[\frac{\partial}{\partial \xi}=\frac{d r}{d \xi} \frac{\partial}{\partial r} \nonumber \]
para que requerimos
\[\frac{d r}{d \xi}=r \text {. } \nonumber \]
Esta sencilla ecuación diferencial se puede resolver si tomamos como nuestra condición límite\(\xi=0\) cuando\(r=1\), correspondiente a los puntos que se encuentran en el límite del obstáculo circular. La solución de\((17.45)\) es, pues, dada por
\[r=e^{\zeta} \nonumber \]
El laplaciano en las llamadas coordenadas polares logarítmicas se convierte entonces
\[\begin{aligned} \nabla^{2} &=\frac{1}{r^{2}}\left(\left(r \frac{\partial}{\partial r}\right)\left(r \frac{\partial}{\partial r}\right)+\frac{\partial^{2}}{\partial \theta^{2}}\right) \\ &=e^{-2 \zeta}\left(\frac{\partial^{2}}{\partial \xi^{2}}+\frac{\partial^{2}}{\partial \theta^{2}}\right) . \end{aligned} \nonumber \]
Además, transformando el lado derecho de\((17.42)\), tenemos
\[\begin{aligned} \frac{1}{r} \frac{\partial \psi}{\partial \theta} \frac{\partial \omega}{\partial r}-\frac{1}{r} \frac{\partial \psi}{\partial r} \frac{\partial \omega}{\partial \theta} &=\frac{1}{r^{2}}\left(r \frac{\partial \omega}{\partial r} \frac{\partial \psi}{\partial \theta}-r \frac{\partial \psi}{\partial r} \frac{\partial \omega}{\partial \theta}\right) \\ &=e^{-2 \xi}\left(\frac{\partial \psi}{\partial \theta} \frac{\partial \omega}{\partial \zeta}-\frac{\partial \psi}{\partial \xi} \frac{\partial \omega}{\partial \theta}\right) . \end{aligned} \nonumber \]
Por lo tanto, las ecuaciones gobernantes para\(\psi=\psi(\xi, \theta)\) y\(\omega=\omega(\xi, \theta)\) en coordenadas log-polares pueden escribirse como
\[\begin{align} -&\left(\frac{\partial^{2}}{\partial \xi^{2}}+\frac{\partial^{2}}{\partial \theta^{2}}\right) \psi=e^{2 \xi} \omega \\ -&\left(\frac{\partial^{2}}{\partial \xi^{2}}+\frac{\partial^{2}}{\partial \theta^{2}}\right) \omega=\frac{\operatorname{Re}}{2}\left(\frac{\partial \psi}{\partial \xi} \frac{\partial \omega}{\partial \theta}-\frac{\partial \psi}{\partial \theta} \frac{\partial \omega}{\partial \xi}\right) . \end{align} \nonumber \]
Aproximación de diferencia finita
Una aproximación de diferencia finita a las ecuaciones gobernantes procede en una cuadrícula en el\((\xi, \theta)\) espacio. La cuadrícula se define para\(0 \leq \xi \leq \zeta_{m}\) y\(0 \leq \theta \leq \pi\), de manera que el dominio computacional forme un rectángulo sin agujeros. Los lados del rectángulo corresponden al límite del obstáculo circular\((\xi=0)\), el arroyo libre\(\left(\xi=\xi_{m}\right)\), la línea media detrás del obstáculo\((\theta=0)\) y la línea media frente al obstáculo\((\theta=\pi)\).
Discretizamos las ecuaciones usando celdas de cuadrícula cuadrada y escribimos
\[\begin{array}{ll} \xi_{i}=i h, & i=0,1, \ldots, n \\ \theta_{j}=j h, & j=0,1, \ldots, m \end{array} \nonumber \]
donde\(n\) y\(m\) son el número de celdas de cuadrícula que abarcan las\(\theta\) direcciones\(\xi\) - y -y\(h\) es la longitud lateral de una celda de cuadrícula. Porque\(0 \leq \theta \leq \pi\), el espaciado de la rejilla debe satisfacer
\[h=\frac{\pi}{m} \nonumber \]
y el valor máximo de\(\xi\) viene dado por
\[\xi_{\max }=\frac{n \pi}{m} \nonumber \]
Por lo tanto, el radio del dominio computacional viene dado por\(e^{\xi \max }\), que se va a comparar con el radio de obstáculo de la unidad. La elección\(n=m\) rendiría\(e^{\zeta_{\max }} \approx 23\), y la elección\(n=2 m\) rendiría\(e^{\zeta_{\max }} \approx 535\). Para realizar un cálculo preciso, es probable que tanto el valor de\(m\) (y\(n\)) como el valor de\(\xi_{\max }\) necesiten aumentar con el número de Reynolds.
Nuevamente hacemos uso del método SOR, usando la notación para el método Jacobi, aunque es probable que se logre una convergencia más rápida usando Gauss-Seidel rojo-negro. La aproximación de diferencia finita a se convierte\((17.47 and 14.48)\) así
\[\psi_{i, j}^{n+1}=\left(1-r_{\psi}\right) \psi_{i, j}^{n}+\frac{r_{\psi}}{4}\left(\psi_{i+1, j}^{n}+\psi_{i-1, j}^{n}+\psi_{i, j+1}^{n}+\psi_{i, j-1}^{n}+h^{2} e^{2 \xi_{i}} \omega_{i, j}^{n}\right), \nonumber \]
y
\[\omega_{i, j}^{n+1}=\left(1-r_{\omega}\right) \omega_{i, j}^{n}+\frac{r_{\omega}}{4}\left(\omega_{i+1, j}^{n}+\omega_{i-1, j}^{n}+\omega_{i, j+1}^{n}+\omega_{i, j-1}^{n}+\frac{\operatorname{Re}}{8} f_{i, j}^{n}\right), \nonumber \]
Dónde
\[f_{i j}^{n}=\left(\psi_{i+1, j}^{n}-\psi_{i-1, j}^{n}\right)\left(\omega_{i, j+1}^{n}-\omega_{i, j-1}^{n}\right)-\left(\psi_{i, j+1}^{n}-\psi_{i, j-1}^{n}\right)\left(\omega_{i+1, j}^{n}-\omega_{i-1, j}^{n}\right) \nonumber \]
Condiciones de contorno
Las condiciones límite deben prescribirse en los lados del dominio computacional rectangular Las condiciones de límite en los dos lados correspondientes a la línea media del dominio físico,\(\theta=0\) y\(\theta=\pi\), satisfacer\(\psi=0\) y\(\omega=0\). La condición de límite en el lado correspondiente al obstáculo circular,\(\xi=0\), se determina nuevamente a partir de las condiciones de no penetración y no deslizamiento, y están dadas por\(\psi=0\) y\(\partial \psi / \partial \xi^{\tau}=0 .\) Y la condición de límite de flujo libre se puede aplicar en \(\xi=\xi_{\max }\).
Primero consideramos la condición de límite de flujo libre. El campo de velocidad de flujo libre adimensional en coordenadas polares se puede encontrar en (17.36),
\[\mathbf{u}=\cos \theta \hat{\mathbf{r}}-\sin \theta \hat{\boldsymbol{\theta}} \nonumber \]
La función stream, por lo tanto, satisface las condiciones de flujo libre
\[\frac{\partial \psi}{\partial \theta}=r \cos \theta, \quad \frac{\partial \psi}{\partial r}=\sin \theta, \nonumber \]
y por inspección, la solución que también satisface\(\psi=0\) cuando\(\theta=0, \pi\) es dada por
\[\psi(r, \theta)=r \sin \theta . \nonumber \]
En las coordenadas log-polares, por lo tanto tenemos la condición de límite de flujo libre
\[\psi\left(\xi_{\max }, \theta\right)=e^{\xi_{\max }} \sin \theta \nonumber \]
Uno tiene dos opciones para la vorticidad en el flujo libre. Se podría tomar la vorticidad en la corriente libre para ser cero, de modo que
\[\omega\left(\xi_{\max }, \theta\right)=0 \nonumber \]
Una segunda opción, más suave, es tomar la derivada de la vorticidad para que sea cero, de manera que
\[\frac{\partial \omega}{\partial \xi}\left(\xi_{\max }, \theta\right)=0 \nonumber \]
Esta segunda opción parece tener propiedades de estabilidad algo mejores para el campo de flujo muy aguas abajo del obstáculo. Idealmente, los valores calculados de interés deben ser independientes de cuál de estas condiciones límite se elige, y encontrar soluciones de campo de flujo usando ambas condiciones de límite proporciona una buena medida de precisión. La condición de límite restante que falta es para la vorticidad sobre el obstáculo. Nuevamente, necesitamos convertir las dos condiciones de límite en la función de flujo,\(\psi=0\) y\(\partial \psi / \partial \xi=0\) a una condición de límite en\(\psi\) y\(\omega\). Desde (17.47 y 17.48), tenemos
\[\omega=-e^{-2 \tilde{}}\left(\frac{\partial^{2} \psi}{\partial \tilde{\xi}^{2}}+\frac{\partial^{2} \psi}{\partial \theta^{2}}\right) \nonumber \]
y ya que en el círculo\(\psi=0\), independiente de\(\theta\)\(\xi=0\), y, tenemos
\[\omega=-\frac{\partial^{2} \psi}{\partial \xi^{2}} \nonumber \]
Una expansión de la serie Taylor a uno y dos puntos de rejilla lejos de los rendimientos de obstáculos circulares
\[\begin{aligned} &\psi_{1, j}=\psi_{0, j}+\left.h \frac{\partial \psi}{\partial \xi}\right|_{(0, j)}+\left.\frac{1}{2} h^{2} \frac{\partial^{2} \psi}{\partial \xi^{2}}\right|_{(0, j)}+\left.\frac{1}{6} h^{3} \frac{\partial^{3} \psi}{\partial \xi^{3}}\right|_{(0, j)}+\mathrm{O}\left(h^{4}\right), \\ &\psi_{2, j}=\psi_{0, j}+\left.2 h \frac{\partial \psi}{\partial \xi}\right|_{(0, j)}+\left.2 h^{2} \frac{\partial^{2} \psi}{\partial \xi^{2}}\right|_{(0, j)}+\left.\frac{4}{3} h^{3} \frac{\partial^{3} \psi}{\partial \xi^{3}}\right|_{(0, j)}+\mathrm{O}\left(h^{4}\right) . \end{aligned} \nonumber \]
Ahora, ambos\(\psi=0\) y\(\partial \psi / \partial \xi=0\) en el punto de la cuadrícula\((0, j) .\) Usando la ecuación para la vorticidad en el círculo,\((17.62)\), da como resultado
\[\begin{aligned} &\psi_{1, j}=-\frac{1}{2} h^{2} \omega_{0, j}+\left.\frac{1}{6} h^{3} \frac{\partial^{3} \psi}{\partial \zeta^{3}}\right|_{(0, j)}+\mathrm{O}\left(h^{4}\right), \\ &\psi_{2, j}=-2 h^{2} \omega_{0, j}+\left.\frac{4}{3} h^{3} \frac{\partial^{3} \psi}{\partial \xi^{3}}\right|_{(0, j)}+\mathrm{O}\left(h^{4}\right) . \end{aligned} \nonumber \]
Multiplicamos la primera ecuación por\(-8\) y la agregamos a la segunda ecuación para eliminar el\(h^{3}\) término. Obtenemos
\[-8 \psi_{1, j}+\psi_{2, j}=2 h^{2} \omega_{0, j}+\mathrm{O}\left(h^{4}\right) \nonumber \]
Resolviendo para la vorticidad, obtenemos nuestra condición límite exacta a segundo orden:
\[\omega_{0, j}=\frac{\psi_{2, j}-8 \psi_{1, j}}{2 h^{2}} \nonumber \]
Las condiciones de contorno se resumen a continuación:
\[\begin{align} \nonumber \xi=0,0 \leq \theta \leq \pi: & \psi_{0, j}=0, \quad \omega_{0, j}=\frac{\psi_{2, j}-8 \psi_{1, j}}{2 h^{2}} ; \\ \xi=\xi_{\max }, 0 \leq \theta \leq \pi: & \psi_{n, j}=e^{\xi_{\max }} \sin j h, \quad \omega_{n, j}=0 \text { or } \omega_{n, j}=\omega_{n-1, j} ; \\ \nonumber 0 \leq \xi \leq \xi_{\max }, \theta=0: & \psi_{i, 0}=0, \quad \omega_{i, 0}=0 ; \\ \nonumber 0 \leq \xi \leq \xi_{\max }, \theta=\pi: & \psi_{i, m}=0, \quad \omega_{i, m}=0 . \end{align} \nonumber \]
Solución usando el método de Newton
Consideramos aquí un método mucho más eficiente para encontrar la solución de flujo constante de fluido. Desafortunadamente, este método también es más difícil de programar. Recordemos de\(\S 7.2\) que el método de Newton puede ser utilizado para resolver un sistema de ecuaciones no lineales. El método de Newton como rutina de búsqueda de raíces tiene la fuerte ventaja de ser muy rápido cuando converge, pero la desventaja de no siempre converger. Aquí, el problema de convergencia se puede superar resolviendo para Re más grande usando como suposición inicial la solución para Re ligeramente más pequeña, con un poco por definir por ensayo y error. Recordemos que el método de Newton puede resolver un sistema de ecuaciones no lineales de la forma
\[F(\psi, \omega)=0, \quad G(\psi, \omega)=0 \nonumber \]
El método de Newton se implementa por escrito
\[\psi^{(k+1)}=\psi^{(k)}+\Delta \psi, \quad \omega^{(k+1)}=\omega^{(k)}+\Delta \omega, \nonumber \]
y el esquema de iteración se deriva linealizando\((17.66)\) en\(\Delta \psi\) y\(\Delta \omega\) para obtener
\[\mathrm{J}\left(\begin{array}{c} \Delta \psi \\ \Delta \omega \end{array}\right)=-\left(\begin{array}{l} F \\ G \end{array}\right) \nonumber \]
donde\(J\) está la matriz jacobiana de las funciones\(F\) y\(G\). Todas las funciones son evaluadas en\(\psi^{(k)}\) y\(\omega^{(k)}\).
Aquí, debemos ver\(\psi\) y\(\omega\) como un gran número de incógnitas y\(F\) y\(G\) un número correspondientemente grande de ecuaciones, donde el número total de ecuaciones necesariamente debe ser igual al número total de incógnitas.
Si reescribimos nuestras ecuaciones gobernantes en la forma dada por (17.66), tenemos
\[\begin{align} \nonumber &-\left(\frac{\partial^{2}}{\partial \xi^{2}}+\frac{\partial^{2}}{\partial \theta^{2}}\right) \psi-e^{2 \xi} \omega=0 \\ &-\left(\frac{\partial^{2}}{\partial \tilde{\xi}^{2}}+\frac{\partial^{2}}{\partial \theta^{2}}\right) \omega-\frac{\operatorname{Re}}{2}\left(\frac{\partial \psi}{\partial \xi} \frac{\partial \omega}{\partial \theta}-\frac{\partial \psi}{\partial \theta} \frac{\partial \omega}{\partial \xi}\right)=0 \end{align} \nonumber \]
Con\(n\) y celdas de\(m\) cuadrícula en las\(\theta\) direcciones\(\xi\) - y -, las ecuaciones diferenciales parciales de (17.69) representan ecuaciones no lineales\(2(n-1)(m-1)\) acopladas para\(\psi_{i, j}\) y\(\omega_{i, j}\) sobre los puntos internos de la rejilla. También incluiremos los valores límite en el vector de solución que agregarán dos incógnitas adicionales y dos ecuaciones para cada punto límite, llevando el número total de ecuaciones (e incógnitas) a\(2(n+1)(m+1)\).
La forma de la matriz jacobiana puede determinarse linealizando (17.69) en\(\Delta \psi\) y\(\Delta \omega\). Usando\((17.67)\), tenemos
\[-\left(\frac{\partial^{2}}{\partial \xi^{2}}+\frac{\partial^{2}}{\partial \theta^{2}}\right)\left(\psi^{(k)}+\Delta \psi\right)-e^{2 \xi}\left(\omega^{(k)}+\Delta \omega\right)=0 \nonumber \]
y
\[\begin{aligned} -\left(\frac{\partial^{2}}{\partial \xi^{2}}+\frac{\partial^{2}}{\partial \theta^{2}}\right)\left(\omega^{(k)}+\Delta \omega\right) & \\ &-\frac{\operatorname{Re}}{2}\left(\frac{\partial\left(\psi^{(k)}+\Delta \psi\right)}{\partial \xi} \frac{\partial\left(\omega^{(k)}+\Delta \omega\right)}{\partial \theta}-\frac{\partial\left(\psi^{(k)}+\Delta \psi\right)}{\partial \theta} \frac{\partial\left(\omega^{(k)}+\Delta \omega\right)}{\partial \xi}\right)=0 . \end{aligned} \nonumber \]
Liinearización en\(\Delta \psi\) y\(\Delta \omega\) luego da como resultado
\[-\left(\frac{\partial^{2}}{\partial \xi^{2}}+\frac{\partial^{2}}{\partial \theta^{2}}\right) \Delta \psi-e^{2 \xi} \Delta \omega=-\left[-\left(\frac{\partial^{2}}{\partial \xi^{2}}+\frac{\partial^{2}}{\partial \theta^{2}}\right) \psi^{(k)}-e^{2 \xi} \omega^{(k)}\right] \nonumber \]
y
\[ \begin{align} -\left(\frac{\partial^{2}}{\partial \xi^{2}}+\frac{\partial^{2}}{\partial \theta^{2}}\right) \Delta \omega &-\frac{\operatorname{Re}}{2}\left(\frac{\partial \omega^{(k)}}{\partial \theta} \frac{\partial \Delta \psi}{\partial \zeta}-\frac{\partial \omega^{(k)}}{\partial \xi} \frac{\partial \Delta \psi}{\partial \theta}+\frac{\partial \psi^{(k)}}{\partial \xi} \frac{\partial \Delta \omega}{\partial \theta}-\frac{\partial \psi^{(k)}}{\partial \theta} \frac{\partial \Delta \omega}{\partial \xi}\right) \nonumber \\ &=-\left[-\left(\frac{\partial^{2}}{\partial \xi ^{2}}+\frac{\partial^{2}}{\partial \theta^{2}}\right) \omega^{(k)}-\frac{\operatorname{Re}}{2}\left(\frac{\partial \psi^{(k)}}{\partial \xi} \frac{\partial \omega^{(k)}}{\partial \theta}-\frac{\partial \psi^{(k)}}{\partial \theta} \frac{\partial \omega^{(k)}}{\partial \xi}\right)\right] \end{align} \nonumber \]
donde la primera ecuación ya era lineal en las\(\Delta\) variables, pero la segunda ecuación originalmente era cuadrática, y los términos cuadráticos ahora se han caído. Se puede observar que las ecuaciones dadas por (17.71) y (17.72) están en la forma de las ecuaciones de iteración de Newton dadas por (17.68).
Numéricamente, ambos\(\Delta \psi\) y\(\Delta \omega\) serán vectores formados por un ordenamiento natural de los puntos de la cuadrícula, como se detalla en\(\$ 6.2\). Estos dos vectores se apilarán entonces en un solo vector como se muestra en (17.68). Para escribir la matriz jacobiana, empleamos la notación taquigráfica\(\partial_{\tau}^{2}=\partial^{2} / \partial \xi^{2}, \psi_{\xi}=\partial \psi / \partial \xi\), y así sucesivamente. La matriz jacobiana puede entonces escribirse simbólicamente como
\[\mathrm{J}=\left(\begin{array}{cc} -\left(\partial_{\xi}^{2}+\partial_{\theta}^{2}\right) & -e^{2 \xi} \mathrm{I} \\ 0 & -\left(\partial_{\xi}^{2}+\partial_{\theta}^{2}\right) \end{array}\right) \quad-\frac{\operatorname{Re}}{2}\left(\begin{array}{cc} 0 & 0 \\ \omega_{\theta} \partial_{\xi}-\omega_{\xi} \partial_{\theta} & \psi_{\xi} \partial_{\theta}-\psi_{\theta} \partial_{\xi} \end{array}\right) \nonumber \]
donde I es la matriz de identidad y las derivadas de\(\psi\) y\(\omega\) en la segunda matriz se evalúan en la iteración\(k\) th.
La matriz jacobiana tal como está escrita es válida para los puntos de cuadrícula interiores al límite, donde cada fila de J corresponde a una ecuación para uno\(\psi\) o\(\omega\) en un punto de cuadrícula interior específico. El operador de tipo Laplaciano está representado por una matriz Laplaciana, y los operadores derivados están representados por matrices derivadas. Los términos\(e^{2 \xi}, \partial \omega / \partial \theta\), y los demás términos derivados deben ser evaluados en el punto de cuadrícula correspondiente a la fila en la que se encuentran.
Para incorporar condiciones de contorno, extendemos los vectores\(\Delta \psi\) e incluimos también los puntos en el límite\(\Delta \omega\) a medida que ocurren en el orden natural de los puntos de la cuadrícula. A la matriz jacobiana y al lado derecho de (17.68) se agregan las ecuaciones apropiadas para las condiciones de contorno en las filas correspondientes a los puntos límite. Al incluir explícitamente los puntos límite en el vector de solución, la matriz Laplaciana precisa de segundo orden y las matrices derivadas presentes en J pueden manejar los puntos de cuadrícula que se encuentran directamente al lado de los límites sin un tratamiento especial.
Las condiciones de límite relevantes que se implementarán son las condiciones de límite en\(\Delta \psi\) y\(\Delta \omega\). Las condiciones de límite en los campos\(\psi\) y\(\omega\) ellos mismos ya han sido dadas por (17.65). Los puntos de cuadrícula con condiciones de contorno fijas encendidas\(\psi\) y\(\omega\) que no cambian con iteraciones tendrán uno en la diagonal en la matriz jacobiana correspondiente a ese punto de cuadrícula, y un cero en el lado derecho. En otras palabras,\(\psi\) y no\(\omega\) cambiará en la iteración del método de Newton, y sus valores iniciales deben elegirse para satisfacer las condiciones de límite apropiadas.
Las dos condiciones de límite que cambian en la iteración, a saber
\[\omega_{0, j}=\frac{\psi_{2, j}-8 \psi_{1, j}}{2 h^{2}}, \quad \omega_{n, j}=\omega_{n-1, j} \nonumber \]
debe implementarse en la iteración del método de Newton como
\[\Delta \omega_{0, j}=\frac{\Delta \psi_{2, j}-8 \Delta \psi_{1, j}}{2 h^{2}}, \quad \Delta \omega_{n, j}=\Delta \omega_{n-1, j} \nonumber \]
y estas ecuaciones ocurren en las filas correspondientes a los puntos de la cuadrícula\((0, j)\) y\((n, j)\), con\(j=0\) a\(m\). Nuevamente, las condiciones iniciales para la iteración deben satisfacer las condiciones de contorno correctas.
La implementación de MATLAB de (17.68) usando (17.73), requiere tanto la construcción de la\((n+1)(m+1) \times(n+1)(m+1)\) matriz que incluye tanto la matriz jacobiana como las condiciones de contorno, y la construcción del lado derecho correspondiente de la ecuación. Para la matriz Laplaciana, se puede hacer uso de la función sp_laplace_new.m; y también se necesita construir las matrices derivadas\(\partial_{\xi}\) y\(\partial_{\theta}\). Ambas matrices están bandeadas, con una banda de positivas por encima de la diagonal principal y una banda de negativas por debajo de la diagonal principal. Para\(\partial_{\xi}\), las bandas están directamente por encima y por debajo de la diagonal. Para\(\partial_{\theta}\), las bandas están a una\(n+1\) distancia de la diagonal, correspondientes a los puntos de\(n+1\) cuadrícula en cada fila. Tanto las matrices laplacianas como las derivadas deben construirse para puntos de\((n+1) \times(m+1)\) cuadrícula y colocarse en una\(2 \times 2\) matriz usando la función kron.m de MATLAB, que genera una matriz de bloques implementando el llamado producto Kronecker. Las filas correspondientes a los puntos de límite deben ser reemplazadas por las ecuaciones para las condiciones de contorno.
El código de MATLAB debe escribirse de manera eficiente, utilizando matrices dispersas. Un perfilado de este código debería mostrar que la mayor parte del tiempo computacional se dedica a resolver (17.68) (con condiciones de límite agregadas) para\(\Delta \psi\) y\(\Delta \omega\) usando el operador de barra invertida de MATLAB. Con\(4 \mathrm{~GB}\) RAM y una computadora portátil comprada circa 2013, y con la resolución\(512 \times 256\) y usando el\(R e=150\) resultado como campo inicial, puedo resolver para\(R e=200\) en siete iteraciones con una precisión de\(10^{-12}\). El tiempo total de ejecución fue aproximadamente\(48 \mathrm{sec}\) con aproximadamente\(42 \mathrm{sec}\) gastado en la sola línea que contenía\(J \backslash \mathrm{b}\).
Visualización de los campos de flujo
Obtener gráficas de contorno correctas de la función del arroyo y la vorticidad puede ser un reto y en esta sección voy a proporcionar alguna orientación. Las funciones básicas de MATLAB requeridas son meshgrid.m, pol2cart.m, contour.m y clabel.m. También se pueden usar funciones más elegantes como contourf.m e imagesc, aunque no voy a discutirlas aquí.
Supongamos que los valores de la función stream son conocidos en una cuadrícula en coordenadas cartesianas bidimensionales. Una gráfica de contorno dibuja curvas siguiendo valores constantes especificados (o predeterminados) de la función de flujo en el\(x-y\) plano. La visualización de las curvas en las que la función de la corriente es constante da una visualización clara del flujo de fluido.
Para hacer el mejor uso de la función contour.m, se especifica la\(x-y\) cuadrícula en la que se conocen los valores de la función stream. La variable de función stream psi, digamos, se da como una\(m\) matriz\(n\) -by-. Examinaremos un ejemplo sencillo para entender cómo organizar los datos.
Supongamos que la función stream es conocida en todos los valores de\(x\) y\(y\) en la cuadrícula bidimensional especificada por\(x=[0,1,2]\) y\(y=[0,1]\). Para etiquetar correctamente el eje de la gráfica de contorno, utilizamos la función meshgrid, y escribimos\([X, Y]=\operatorname{meshgrid}(X, Y)\). Los valores asignados a\(X\) y\(Y\) son las siguientes matrices 2 -por-3:
\[X=\left[\begin{array}{lll} 0 & 1 & 2 \\ 0 & 1 & 2 \end{array}\right], \quad Y=\left[\begin{array}{lll} 0 & 0 & 0 \\ 1 & 1 & 1 \end{array}\right] \nonumber \]
La variable psi debe tener las mismas dimensiones que las variables\(X\) y\(Y\). Supongamos que psi viene dado por
\[\text { psi }=\left[\begin{array}{lll} a & b & c \\ d & e & f \end{array}\right] \nonumber \]
Entonces los datos deben organizarse de manera que psi\(=a\) at\((x, y)=(0,0)\), psi\(=b\) at\((x, y)=(1,0)\), psi\(=d\) at\((x, y)=(0,1)\), etc. observe que los valores de psi a través de una fila\((\mathrm{psi}(i, j), j=1: 3)\) corresponden a diferentes \(x\)ubicaciones, y los valores de psi hacia abajo de una columna\(((p s i(i, j), i=1: 2))\) corresponden a diferentes\(y\) ubicaciones. Aunque esto es visualmente intuitivo ya que\(x\) corresponde a la variación horizontal y\(y\) a la variación vertical, es algebraicamente contradictorio: el primer índice de psi corresponde a la\(y\) variación y el segundo índice corresponde al \(x\)variación. Si uno usa la notación psi\((x, y)\) durante el cálculo, entonces para trazar uno necesita tomar la transposición de la matriz psi.
Ahora el cálculo del campo de flujo alrededor de un círculo se realiza usando coordenadas log-polares\((\xi, \theta)\). Para construir una gráfica de contorno, los campos de solución necesitan transformarse en coordenadas cartesianas. La función de MATLAB pol2cart.m proporciona una solución sencilla. Se definen las variables theta y xi que definen la malla en coordenadas log-polares, y luego primero se transforma en coordenadas polares estándar con\(r=\exp (x i)\). La cuadrícula de coordenadas polares se construye a partir de [THETA, R] =rejilla de malla (theta,\(r\)), y la cuadrícula cartesiana se construye a partir de
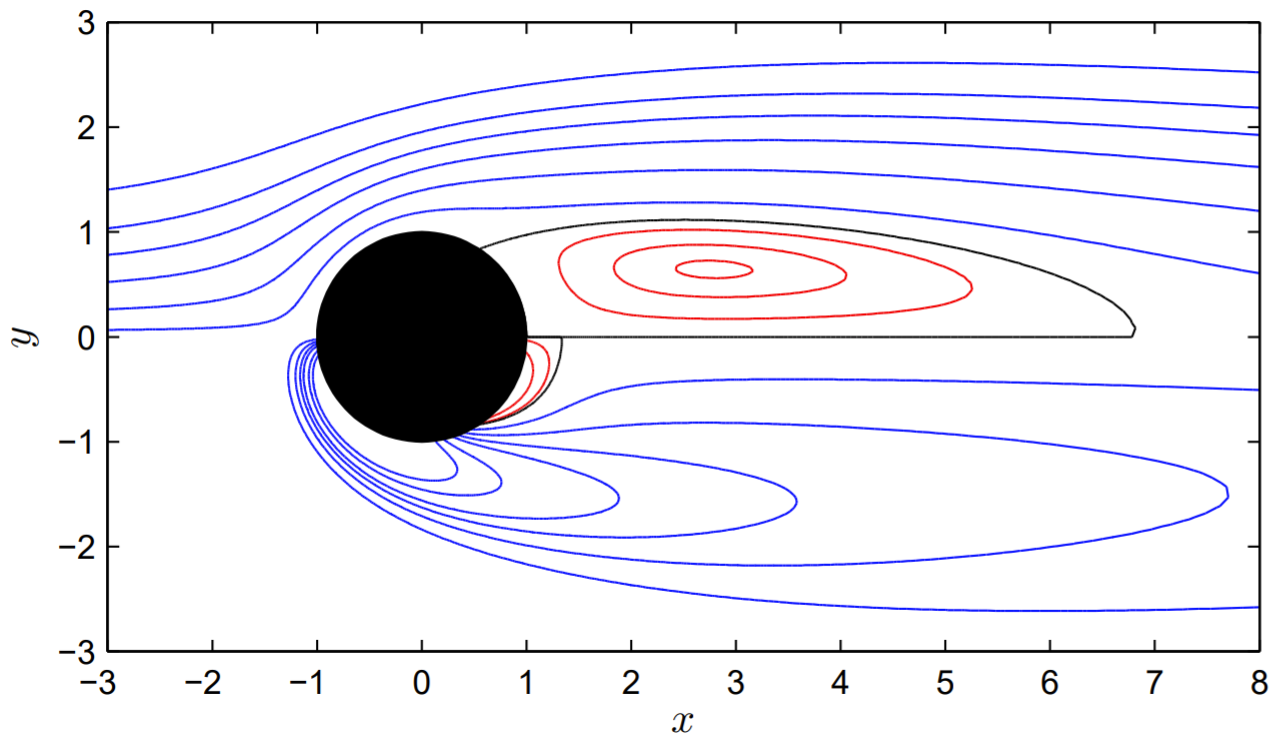
\(\left[\begin{array}{ll}X, & Y\end{array}\right]=\)pol 2 carro\((\) THETA,\(R)\). Los campos se pueden trazar directamente usando la cuadrícula cartesiana, aunque esta cuadrícula no sea uniforme. Es decir, se puede hacer una gráfica de contorno simple con el comando contour\((X, Y, p s i)\). Las llamadas más sofisticadas a contorno.m especifican las curvas de nivel precisas que se van a trazar, y su etiquetado usando clabel.m.
Una buena manera de trazar tanto la función de flujo como los campos de vorticidad en una sola gráfica es trazar los contornos de la función de flujo para\(y>0\) y los contornos de vorticidad para\(y<0\), haciendo uso de la simetría de los campos alrededor del\(x\) eje -eje. A modo de ilustración, en la Fig. 17.1\(\operatorname{Re}=50\) se muestra una gráfica de la función del arroyo y los contornos de vorticidad para.

