5.2: La matriz de “adyacencia”

La forma más común de matriz en el análisis de redes sociales es una matriz cuadrada muy simple con tantas filas y columnas como actores haya en nuestro conjunto de datos. Los “elementos” o puntuaciones en las celdas de la matriz registran información sobre los vínculos entre cada par de actores.

La matriz más simple y común es la binaria. Es decir, si está presente un empate, se ingresa uno en una celda; si no hay empate, se ingresa un cero. Este tipo de matriz es el punto de partida para casi todos los análisis de redes, y se llama “matriz de adyacencia” porque representa quién está al lado, o adyacente a quién en el “espacio social” mapeado por las relaciones que hemos medido.

Una matriz de adyacencia puede ser “simétrica” o “asimétrica”. La distancia social puede ser simétrica o asimétrica. Si Bob y Carol son “amigos” comparten un “lazo unido” y la entrada en la celda X _{i, j} será la misma que la entrada en la celda X _{j, i}.

Pero la distancia social puede ser algo gracioso (no euclidiano). Bob puede sentirse cercano a Carol, pero Carol puede que no sienta lo mismo por Bob. En este caso, el elemento que muestra la relación de Bob con Carol sería anotado “1", mientras que el elemento que muestra la relación de Carol con Bob sería anotado “0”. Es decir, en una matriz “asimétrica”, X _{i, j} no es necesariamente igual a X _{j, i}.

Por convención, en una matriz dirigida (es decir, asimétrica), el emisor de un empate es la fila y el objetivo del empate es la columna. Veamos un ejemplo sencillo. La gráfica dirigida de elecciones de amistad entre Bob, Carol, Ted y Alice se muestra en la figura 5.4.

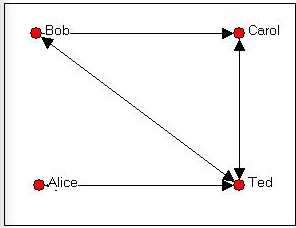
Figura 5.4. Bob, Carol, Ted y Alice

Podemos ya que los lazos se miden a nivel nominal (es decir, los datos son datos de elección binaria), podemos representar la misma información en una matriz que se parece a:

	Bob	Carol	Ted	Alice
Bob	—	1	1	0
Carol	0	—	1	0
Ted	1	1	—	1
Alice	0	0	1	—

Figura 5.5. Matriz asimétrica de adyacencia de la gráfica mostrada en la Figura 5.4.

Recuerda que las filas representan la fuente de los lazos dirigidos, y las columnas los blancos; Bob elige aquí a Carol, pero Carol no elige a Bob. Este es un ejemplo de una matriz “asimétrica” que representa lazos dirigidos (lazos que van de una fuente a un receptor). Es decir, el elemento i, j no necesariamente iguala al elemento j, i. Si los lazos que estábamos representando en nuestra matriz eran “vinculados-lazos” (por ejemplo, los lazos que representan la relación “es un socio comercial de” o “co-ocurrencia o copresencia”, (por ejemplo, donde los lazos representan una relación como: “sirve en la misma junta directiva como”) la matriz necesariamente sería simétrica; es decir, el elemento i, j sería igual al elemento j, i.

Los datos de elección binaria se suelen representar con ceros y unos, indicando la presencia o ausencia de cada relación lógicamente posible entre pares de actores.

Las gráficas firmadas se representan en forma de matriz (generalmente) con -1, 0 y +1 para indicar relaciones negativas, relaciones nulas o neutrales, y relaciones positivas. Las gráficas “firmadas” son en realidad una versión especializada de una relación ordinal.

Cuando los lazos se miden a nivel ordinal o de intervalo, la magnitud numérica del empate medido se ingresa como el elemento de la matriz. Como comentamos anteriormente, son posibles otras formas de datos (nominales multicategorias, ordinales con más de tres rangos, orden nominal de rango completo). Estas otras formas, sin embargo, rara vez se utilizan en estudios sociológicos, y no les vamos a dar mucha atención.

Al representar los datos de redes sociales como matrices, siempre surge la pregunta: ¿qué hago con los elementos de la matriz donde i = j? Es decir, por ejemplo, ¿Bob se considera a sí mismo como un amigo cercano de Bob? Esta parte de la matriz se llama la diagonal principal. A veces el valor de la diagonal principal no tiene sentido, y se ignora (y se deja en blanco o se rellena con ceros o unos). A veces, sin embargo, la diagonal principal puede ser muy importante, y puede tomar valores significativos. Esto es particularmente cierto cuando las filas y columnas de nuestra matriz son “supernodos” o “bloques”. Más sobre eso en un minuto.

A menudo es conveniente referirse a ciertas partes de una matriz usando terminología taquigráfica. Si tomo todos los elementos de una fila (por ejemplo, a quien Bob eligió como amigos: —,1,1,0) estoy examinando el "vector de fila" para Bob. Si sólo miro quién eligió a Bob como amigo (la primera columna, o —,0,1,0), estoy examinando el "vector de columna" para Bob. A veces es útil realizar ciertas operaciones en vectores de fila o columna. Por ejemplo, si resumiera los elementos de los vectores de columna en este ejemplo, estaría midiendo cuán “popular” era cada nodo (en términos de la frecuencia con la que eran el blanco de un vínculo de amistad dirigido). Entonces un “vector” puede ser una matriz completa (1 x... o... x 1), o una parte de una matriz más grande.