16.3: Álgebra de roles para datos Mulitplex

Supongamos que estábamos viendo una sola matriz sobre quién era amigo de quién. Una forma obvia de caracterizar lo que vemos es clasificar a cada pareja como “amigos” o “no amigos”. Pero ahora, extendamos nuestro análisis un paso más allá (o veamos caminos de longitud 2). Ahora cada par de actores podría caracterizarse como amigo, no amigo, amigo de amigo, amigo de no amigo, no amigo de amigo, o no amigo de no-amigo. Si quisiéramos considerar caminos de longitud tres... bueno, entiendes la idea.

La noción de “álgebra de roles” es entender las relaciones entre actores como realizaciones de los “compuestos” lógicamente posibles de relaciones de longitudes de trayectoria seleccionadas. La mayoría de las veces en los análisis de redes, nos enfocamos en el camino de longitud uno (dos actores están conectados o no). Pero, a veces es útil caracterizar una gráfica como que contiene tipos de relaciones más complejas (amigo de amigo, no amigo de amigo, etc.). Las listas de este tipo de relaciones se pueden obtener tomando productos booleanos de matrices (es decir, 0 * 0 = 0, 0 * 1 = 0, 1 * 0 = 0 y 1 * 1 = 1). Cuando se aplica a una sola matriz, elevamos una matriz a una potencia (la multiplicamos por sí misma) y tomamos el producto booleano; el resultado genera una matriz que nos dice si existe una relación entre cada par de nodos que es de una longitud de ruta igual a la potencia. Es decir, para saber si cada par de actores está conectado por la relación “amigo de un amigo” tomamos al cuadrado el producto booleano de la matriz de amistad.

Este método (elegante, pero más bien misterioso) de encontrar “relaciones compuestas” se puede aplicar a los datos multiplex como una forma de identificar los tipos de relaciones que existen en una gráfica multiplex. El algoritmo Transform>Semigrupo puede ser utilizado para identificar estos tipos cualitativos más complejos de relaciones entre nodos.

Es más fácil para la mayoría de la gente entender esto con un ejemplo, que en abstracto. Entonces hagamos un examen algo extendido de los datos de Knoke tanto para información como para lazos monetarios.

Si consideramos solo las relaciones directas, hay dos: las organizaciones pueden estar atadas por la información; las organizaciones pueden estar atadas por el dinero. ¿Y si consideramos las relaciones en dos pasos (lo que se llaman “longitudes de palabras” en el álgebra de roles)? Además de las dos relaciones originales, ahora hay cuatro más:

• Cuando multiplicamos la matriz de información por su transposición y tomamos productos booleanos, estamos identificando enlaces como “envía información a un nodo que envía información a...”
• Cuando multiplicamos la matriz monetaria por su transposición y tomamos productos booleanos, estamos identificando el vínculo: “envía dinero a un nodo que envía dinero a...”
• Cuando multiplicamos la matriz de información por la matriz monetaria, estamos identificando la relación: “envía información a un nodo que envía dinero a...”
• Cuando multiplicamos la matriz monetaria por la matriz de información, estamos identificando la relación: “envía dinero a un nodo que envía información a...”

Estas cuatro nuevas relaciones (de dos pasos) entre los nodos son “palabras” de longitud dos, o “compuestos”.

Es posible, por supuesto, seguir componiéndose a longitudes aún mayores. En la mayoría de los análisis sociológicos con solo dos tipos de lazos, las longitudes más largas rara vez son sustantivamente significativas. Con más tipos de lazos, sin embargo, el número de tipos de relaciones compuestas puede llegar a ser bastante grande con bastante rapidez.

La herramienta Transform>Semigrupo calcula todos los tipos de relaciones compuestas lógicamente posibles hasta una longitud de palabra (es decir, distancia de red) que el usuario especifique. Produce un archivo de registro que contiene un “mapa” de los tipos de relaciones, como vemos en la Figura 16.9. También produce, en un archivo separado, matrices de adyacencia para cada uno de los tipos de relaciones (Figuras 16.10 y 16.11).

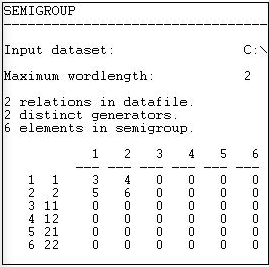
Figura 16.9: Semigrupos de palabra de longitud 2 para redes de información y dinero de Knoke

El resultado nos dice que hubo dos relaciones (información y dinero). Estos fueron los “generadores” que se utilizaron para crear los tipos. Se generaron seis posibles relaciones compuestas para la longitud de palabra 2 (identificada en el lado izquierdo). Las relaciones 1 y 2 son información y dinero individualmente - las matrices originales. La relación 3 es un compuesto de información consigo misma; la relación cuatro es el compuesto de información con dinero, etc. Los números (3, 4, 5, 6) son simplemente guías a qué matriz en el archivo de salida se refiere a qué relación.

A partir de estos nuevos “tipos” de relaciones (que son compuestos dentro y entre los dos tipos de vínculos) podemos generar nuevas matrices de adyacencia que muestran qué pares de actores están unidos por cada tipo particular de relación. Estas se presentan como una serie de matrices de adyacencia, como se muestra en la Figura 16.10 y continuadas en la Figura 16.11.

Figura 16.10: Tablas de relaciones para la Figura 16.9 (parte 1)

La matriz 1 es simplemente la matriz de información original; la matriz 2 es la matriz monetaria original. La matriz 3 es el compuesto de información con información -qué actores están atados por una relación “El ego envía información a alguien que envía información a Alter”?

Figura 16.11: Tablas de relaciones para la Figura 16.9 (parte 2)

Matrix 4 es el compuesto del dinero consigo mismo, o “Ego envía dinero a alguien que envía dinero a Alter”.

Las matrices 5 y 6 son, de alguna manera, las más interesantes. Si bien el intercambio de información por información y dinero por dinero son formas obvias en las que se puede integrar una red, también es posible que los actores puedan integrarse mediante relaciones que involucren tanto a “manzanas” como a “naranjas”. Es decir, puedo enviar dinero, y recibir información; puedo enviar información, y recibir dinero.

El álgebra de roles ha demostrado ser de particular valor en el estudio de las relaciones de parentesco, donde los lazos generacionales (padre/hijo) se registran en una matriz y las relaciones dentro de la generación se registran en otra. Los diversos compuestos (por ejemplo, “hijo de niño”, “hijo de hermano”) capturan con bastante facilidad los términos significativos en las relaciones de parentesco.