11.1: Definición de Autómatas Celulares
- Page ID
- 115734
“Autómata” (plural: “autómatas”) es un término técnico utilizado en informática y matemáticas para una máquina teórica que cambia su estado interno con base en insumos y su estado anterior. El conjunto de estados generalmente se define como finito y discreto, lo que a menudo causa no linealidad en la dinámica del sistema.
Los autómatas celulares (CA) [18] son un conjunto de tales autómatas dispuestos a lo largo de una cuadrícula espacial regular, cuyos estados se actualizan simultáneamente mediante una función de transición de estado aplicada uniformemente que se refiere a los estados de sus vecinos. Dicha actualización simultánea también se denomina actualización sincrónica (que podría aflojarse para ser asíncrona; para ser discutida más adelante). La idea original de CA fue inventada en las décadas de 1940 y 1950 por John von Neumann y su colaborador Stanisław Ulam. Inventaron este marco de modelado, que fue uno de los primeros en modelar sistemas complejos, con el fin de describir el comportamiento auto-reproductivo y evolutivo de los sistemas vivos [11].
Debido a que los CA son muy poderosos para describir dinámicas espacio-temporales altamente no lineales de una manera simple y concisa, han sido ampliamente utilizados para modelar diversos fenómenos, como dinámica molecular, hidrodinámica, propiedades físicas de los materiales, procesos químicos de reacción-difusión, crecimiento y morfogénesis de un organismo vivo, interacción ecológica y evolución de poblaciones, propagación de atascos, dinámicas sociales y económicas, etc. También se han utilizado para aplicaciones computacionales como procesamiento de imágenes, generación de números aleatorios y criptografía.
Hay algunas definiciones técnicas y terminologías que necesita conocer para discutir los modelos de CA, así que aquí viene un aluvión de definiciones.
Matemáticamente hablando, las CA se definen como un sistema dinámico distribuido espacialmente donde tanto el tiempo como el espacio son discretos. Un modelo de CA consiste en autómatas idénticos (celdas o sitios) uniformemente dispuestos en puntos de celosía en un espacio discreto D-dimensional (generalmente\(D = 1, 2,\) o\(3)\). Cada autómata es una variable dinámica, y su cambio temporal viene dado por
\[s_{t+1}(x)=F(s_{t}(x+x_{0}), s_{t}(x+x_{1}), ..., s_{t}(x+x_{n-1})), \label{(11.1)} \]
donde\(s_{t}(x)\) se encuentra el estado de un autómata en su\(x\) momento\(t\),\(F\) es la función de transición de estado, y\(N = {x_0,x_1,...,x_{n−1}}\) es el vecindario. La idea de que la misma función statetransition y la misma vecindad se aplican uniformemente a todas las ubicaciones espaciales es la suposición más característica de CA. Cuando von Neumann y Ulam desarrollaron este marco de modelado, los investigadores generalmente no tenían datos empíricos explícitos sobre cómo se conectaban las cosas en sistemas complejos del mundo real. Por lo tanto, fue un primer paso razonable asumir la regularidad y homogeneidad espacial (que se extenderá posteriormente en modelos de red).
\(s_t\)es una función que mapea ubicaciones espaciales a estados, lo que se denomina configuración de la CA en el momento\(t\). Una configuración intuitivamente significa el patrón espacial que la CA muestra en ese momento. Estas definiciones se ilustran en la Fig. 11.1.1.
\(N\)El vecindario generalmente se configura de manera que se centra alrededor de la célula focal que se actualiza\((x_0 = 0)\) y se localiza espacialmente\((|x_i −x_0| ≤ r\) para\(i = 1,2,...,n−1)\), donde r se llama un radio de\(N\). En otras palabras, el siguiente estado de una célula se determina localmente de acuerdo con su propio estado actual y los estados actuales de sus vecinos locales. Un arreglo específico de estados dentro del barrio se llama situación aquí. La Figura 11.1.2 muestra ejemplos típicos de vecindarios frecuentemente utilizados para AC bidimensional. En CA con barrios von Neumann (Fig. 11.1.2, izquierda), cada celda cambia su estado de acuerdo con los estados de sus celdas vecinas superior, inferior, derecha e izquierda así como a sí misma. Con los barrios Moore (Fig. 11.1.2, derecha), se suman cuatro celdas diagonales al barrio.
La función de transición de estado se aplica de manera uniforme y simultánea a todas las celdas del espacio. La función se puede describir en forma de tabla de consulta (como se muestra en la figura 11.1.1), alguna fórmula matemática o un lenguaje algorítmico de más alto nivel.
Si una función de transición de estado siempre da un estado idéntico a todas las situaciones que son idénticas entre sí cuando se rotan, entonces el modelo de CA tiene simetría rotacional. Tal simetría se emplea a menudo en CA con el objetivo de modelar fenómenos físicos. La simetría rotacional se llama fuerte si todos los estados de la CA están libres de orientación y si la rotación de una situación no implica ninguna rotación de los propios estados (Fig. 11.1.3, izquierda). De lo contrario, se le llama débil (Fig. 11.1.3, derecha). En CA con simetría rotacional débil, algunos estados están orientados, y la rotación de una situación requiere ajustes rotacionales de esos estados también. El modelo AC original de Von Neumann adoptó una débil simetría rotacional.
Si una función de transición de estado depende únicamente de la suma de los estados de las celdas dentro de la vecindad, la CA se llama totalista. Por definición, tales funciones de transición de estado son rotacionalmente simétricas. La suposición totalista hace que el diseño de los modelos de CA sea mucho más simple, sin embargo, aún pueden producir una amplia variedad de dinámicas complejas [34].
Los estados de CA generalmente se categorizan como quiescentes o no quiescentes. Una célula en estado de reposo permanece en el mismo estado si todos sus vecinos también están en el mismo estado de reposo. Muchos modelos de CA tienen al menos uno de esos estados de reposo, a menudo representados por “0” o “” (en blanco). Este estado simboliza un “vacío” en el universo CA. Los estados no quiescentes también se denominan estados activos, porque pueden cambiar dinámicamente e interactuar con estados cercanos. Dichos estados activos suelen desempeñar un papel principal en la producción de comportamientos complejos dentro de la CA.
Debido a que los modelos de CA tienen una extensión espacial así como una extensión temporal, es necesario especificar condiciones de límite espacial además de condiciones iniciales para estudiar sus comportamientos. Hay varias condiciones de límite comúnmente adoptadas:
Esto supone que el espacio es infinito y completamente lleno del estado de reposo
Esto supone que el espacio está “envuelto alrededor” de cada eje espacial, es decir, las celdas en un borde de un espacio finito están conectadas a las celdas en el borde opuesto. Los ejemplos incluyen un anillo para CA 1-D y un toro para CA 2-D
Esto supone que las celdas en el borde de un espacio finito no tienen vecinos más allá de los límites. Esto necesariamente da como resultado un menor número de vecinos, y por lo tanto, la función de transición de estado debe diseñarse para que pueda manejar tales casos.
Esto supone que las celdas en el borde de un espacio finito tienen estados fijos que nunca cambiarán. Esta suele ser la opción más fácil cuando implementa un código de simulación de un modelo de CA
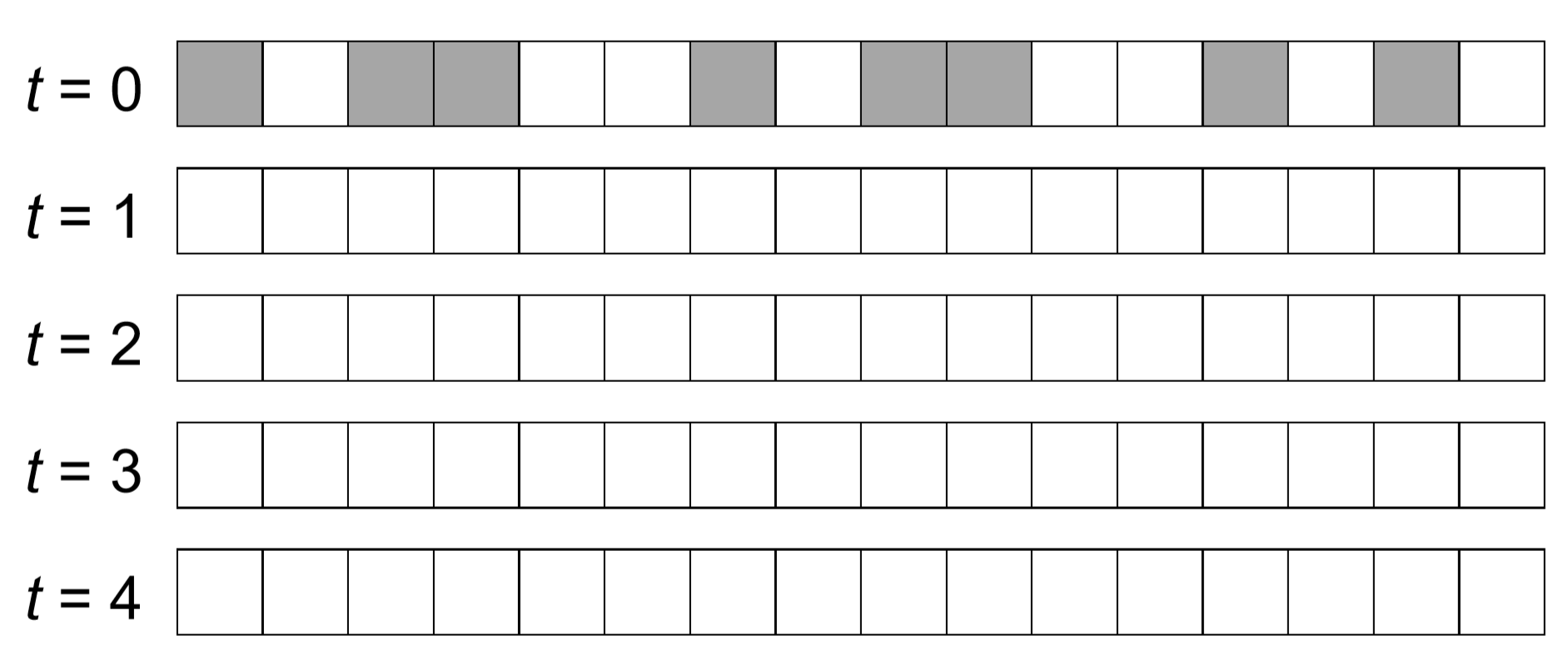
A continuación se muestra un ejemplo de un modelo de CA totalista unidimensional con radio 1 y una condición de límite periódico. Blanco significa 0, mientras que gris significa 1. Cada celda cambia a round (S/3) en cada paso de tiempo, donde S es la suma local de estados dentro de su vecindario. Completar la evolución temporal de esta CA.
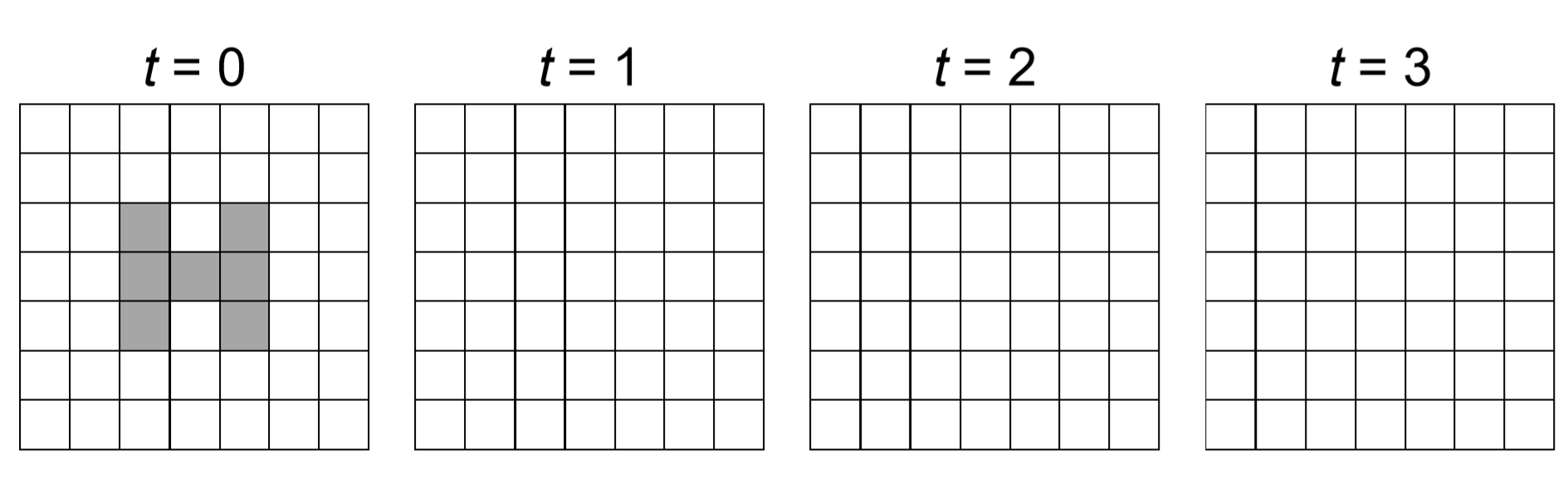
A continuación se muestra un ejemplo de un modelo de CA totalista bidimensional con barrios de von Neumann y sin condiciones límite (espacio infinito). Blanco significa 0 (= estado quiescente), mientras que gris significa 1. Cada celda cambia a round (S/5) en cada paso de tiempo, donde S es la suma local de los estados dentro de su vecindario. Completar la evolución temporal de esta CA.