11.2: Teoría de la bifurcación
- Page ID
- 119190
Una bifurcación ocurre en una ecuación diferencial no lineal cuando un pequeño cambio en un parámetro da como resultado un cambio cualitativo en la solución a largo plazo. Ejemplos de bifurcaciones son cuando se crean o destruyen puntos fijos, o cambian su estabilidad.
a)
b)
Ahora consideramos cuatro bifurcaciones clásicas de ecuaciones diferenciales no lineales unidimensionales: bifurcación de nodo de silla de montar, bifurcación transcrítica, bifurcación de horca supercrítica y bifurcación de horca subcrítica. La ecuación diferencial correspondiente se escribirá como
\[\dot{x}=f_{r}(x), \nonumber \]
donde el subíndice\(r\) representa un parámetro que da como resultado una bifurcación cuando se varía a través de cero. Las ecuaciones diferenciales más simples que exhiben estas bifurcaciones se denominan las formas normales, y corresponden a un análisis local (es decir, expansión de la serie Taylor) de ecuaciones diferenciales más generales alrededor del punto fijo, junto con una posible reescalación de\(x\).
11.2.1. Bifurcación de nodo de silla de montar
La bifurcación del nodo de silla da como resultado la creación o destrucción de puntos fijos. La forma normal para una bifurcación de nodo de silla de montar viene dada por
\[\dot{x}=r+x^{2} . \nonumber \]
Los puntos fijos son\(x_{*}=\pm \sqrt{-r}\). Claramente, existen dos puntos fijos reales cuando\(r<0\) y no existen puntos fijos reales cuando\(r>0\). La estabilidad de los puntos fijos cuando\(r<0\) están determinados por la derivada de\(f(x)=r+x^{2}\), dada por\(f^{\prime}(x)=2 x\). Por lo tanto, el punto fijo negativo es estable y el punto fijo positivo es inestable.
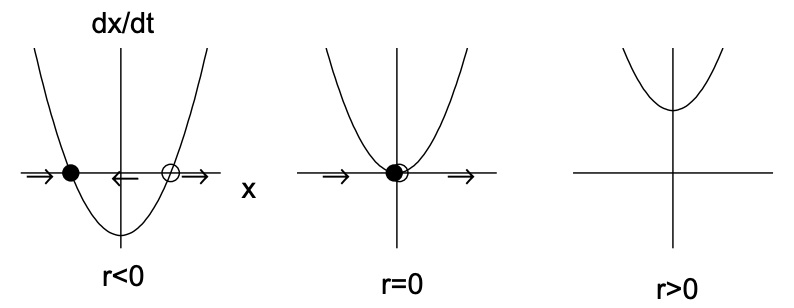
Gráficamente, podemos ilustrar esta bifurcación de dos maneras. Primero, en la Fig. 11.2 (a), trazamos\(\dot{x}\) versus\(x\) para los tres valores de parámetros correspondientes a\(r<0, r=0\) y
a)
b)
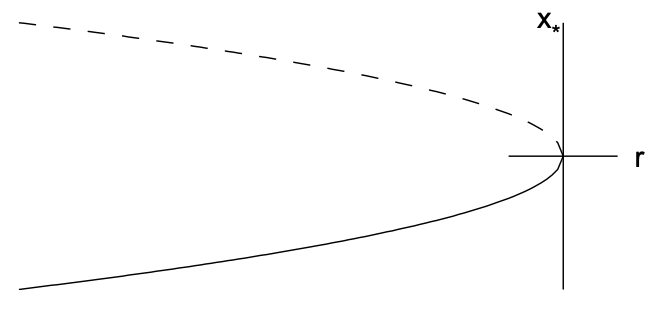
\(r>0\). Los valores en los que\(\dot{x}=0\) corresponden a los puntos fijos, y se dibujan flechas que indican cómo\(x(t)\) evoluciona la solución (a la derecha si\(\dot{x}>0\) y a la izquierda si\(\dot{x}<0\)). El punto fijo estable se indica mediante un círculo relleno y el punto fijo inestable por un círculo abierto. Tenga en cuenta que cuando\(r=0\), las soluciones convergen al origen desde la izquierda, pero divergen del origen de la derecha. Segundo, en la Fig. 11.2 (b), trazamos un diagrama de bifurcación que ilustra el punto fijo\(x_{*}\) versus el parámetro de bifurcación\(r\). El punto fijo estable se denota con una línea continua y el punto fijo inestable por una línea discontinua. Tenga en cuenta que los dos puntos fijos chocan y aniquilan en\(r=0\), y no hay puntos fijos para\(r>0\).
11.2.2. Bifurcación transcrítica
Una bifurcación transcrítica ocurre cuando hay un intercambio de estabilidades entre dos puntos fijos. La forma normal para una bifurcación transcrítica viene dada por
\[\dot{x}=r x-x^{2} \nonumber \]
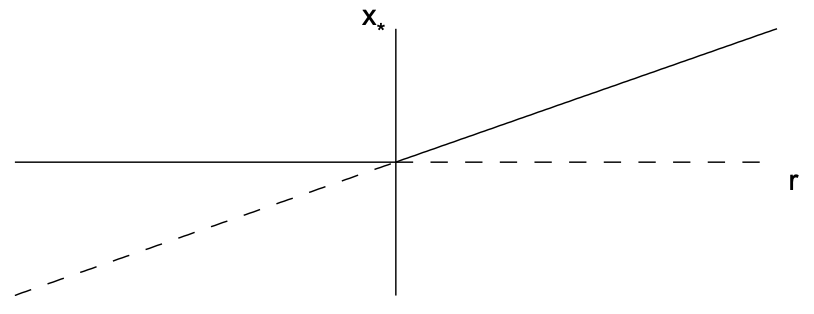
Los puntos fijos son\(x_{*}=0\) y\(x_{*}=r\). El derivado del lado derecho es\(f^{\prime}(x)=r-2 x\), para que\(f^{\prime}(0)=r\) y\(f^{\prime}(r)=-r\). Por lo tanto, for\(r<0, x_{*}=0\) es estable y\(x_{*}=r\) es inestable, mientras que for\(r>0, x_{*}=r\) es estable y\(x_{*}=0\) es inestable. Los dos puntos fijos intercambian así la estabilidad a medida que\(r\) pasa por cero. La bifurcación transcrítica se ilustra en la Fig. 11.3.
a)
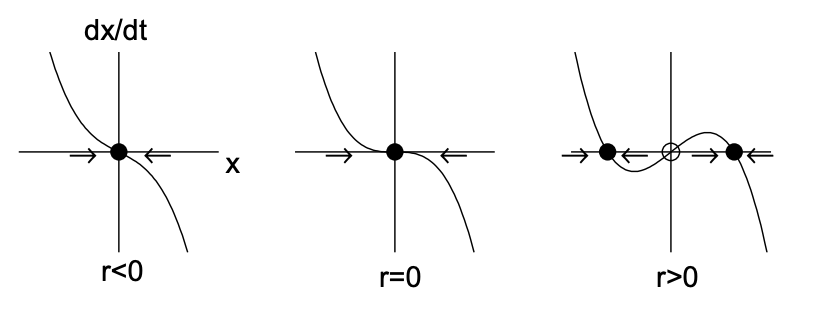
b)
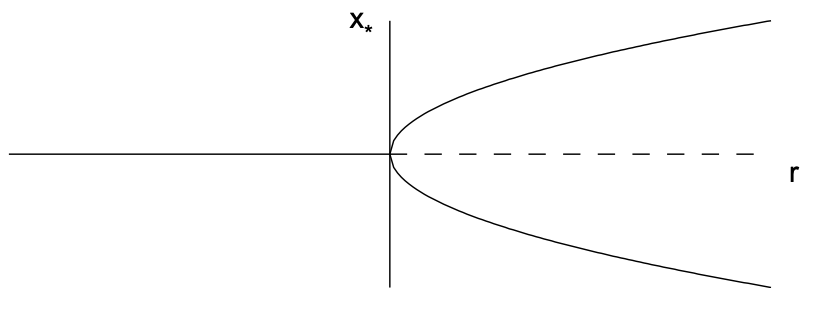
11.2.3. Bifurcación de tricada supercrítica
Las bifurcaciones de horca ocurren en modelos físicos donde aparecen puntos fijos y desaparecen en pares debido a alguna simetría intrínseca del problema. Las bifurcaciones de horca pueden venir en uno de dos tipos. En la bifurcación supercrítica, se crean un par de puntos fijos estables en el punto de bifurcación (o crítico) y existen después de (súper) la bifurcación. En la bifurcación subcrítica, se crea un par de puntos fijos inestables en el punto de bifurcación y existen antes de (sub) la bifurcación.
La forma normal para la bifurcación supercrítica de horca viene dada por
\[\dot{x}=r x-x^{3} . \nonumber \]
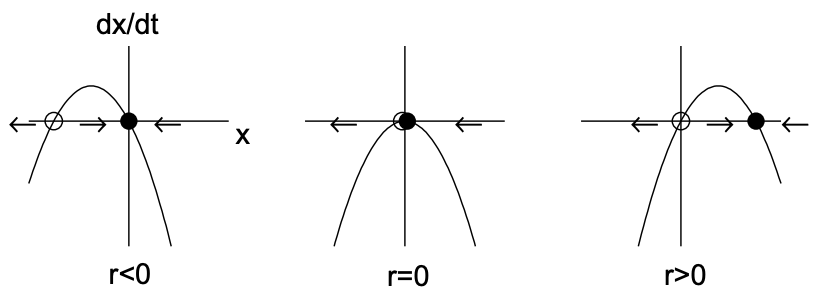
Tenga en cuenta que el término lineal da como resultado un crecimiento exponencial cuando\(r>0\) y el término no lineal estabiliza este crecimiento. Los puntos fijos son\(x_{*}=0\) y\(x_{*}=\pm \sqrt{r}\), estos últimos puntos fijos existentes sólo cuando\(r>0\). El derivado de\(f\) es\(f^{\prime}(x)=r-3 x^{2}\) para que\(f^{\prime}(0)=r\) y\(f^{\prime}(\pm \sqrt{r})=-2 r\). Por lo tanto, el punto fijo\(x_{*}=0\) es estable para\(r<0\) e inestable\(r>0\) mientras los puntos fijos\(x=\pm \sqrt{r}\) existen y son estables para\(r>0\). Observe que el punto fijo\(x_{*}=0\) se vuelve inestable a medida que\(r\) cruza cero y\(x_{*}=\pm \sqrt{r}\) nacen dos nuevos puntos fijos estables. La bifurcación supercrítica de horca se ilustra en la Fig. 11.4.
11.2.4. Bifurcación de horca subcrítica
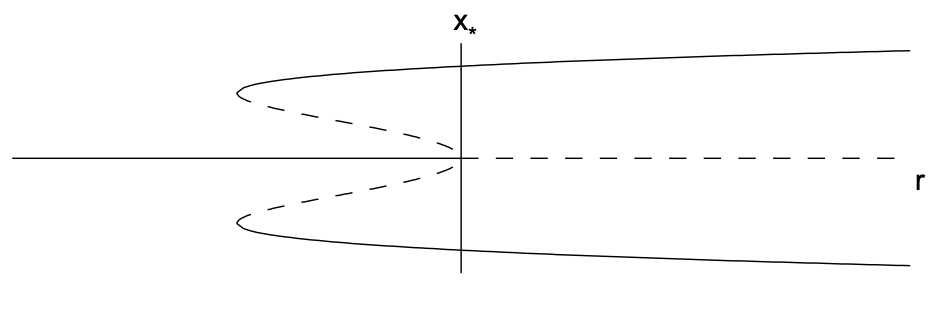
En el caso subcrítico, el término cúbico es desestabilizador. La forma normal (ordenar\(\left.x^{3}\right)\) es
\[\dot{x}=r x+x^{3} . \nonumber \]
Los puntos fijos son\(x_{*}=0\) y\(x_{*}=\pm \sqrt{-r}\), estos últimos puntos fijos existentes sólo cuando\(r \leq 0\). El derivado del lado derecho es\(f^{\prime}(x)=r+3 x^{2}\) así que\(f^{\prime}(0)=r\) y\(f^{\prime}(\pm \sqrt{-r})=-2 r\). Por lo tanto, el punto fijo\(x_{*}=0\) es estable para\(r<0\) e inestable\(r>0\) mientras los puntos fijos\(x=\pm \sqrt{-r}\) existen y son inestables para\(r<0\). No hay puntos fijos estables cuando\(r>0\).
La ausencia de puntos fijos estables para\(r>0\) indica que el descuido de términos de orden\(x\) superior en que\(x^{3}\) en la forma normal puede ser injustificado. Manteniendo la simetría intrínseca de las ecuaciones (solo potencias impares de\(x\)) podemos agregar un término estabilizador no lineal proporcional a\(x^{5}\). La forma normal extendida (a la orden\(x^{5}\)) es
\[\dot{x}=r x+x^{3}-x^{5}, \nonumber \]
y es algo más difícil de analizar. Los puntos fijos son soluciones de
\[x\left(r+x^{2}-x^{4}\right)=0 \nonumber \]
El punto fijo\(x_{*}=0\) existe para todos\(r\), y se pueden encontrar cuatro puntos fijos adicionales a partir de las soluciones de la ecuación cuadrática en\(x^{2}\):
\[x_{*}=\pm \sqrt{\frac{1}{2}(1 \pm \sqrt{1+4 r})} . \nonumber \]
Estos puntos fijos existen sólo si\(x_{*}\) es real. Claramente, para que la raíz cuadrada interior sea real,\(r \geq-1 / 4\). También observa que\(1-\sqrt{1+4 r}\) se vuelve negativo para\(r>0\). Por lo tanto, tenemos tres intervalos\(r\) a considerar, y estas regiones y sus puntos fijos son
\[\begin{array}{cl} r<-\frac{1}{4}: & x_{*}=0 \quad \text { (one fixed point); } \\ -\frac{1}{4}<r<0: \quad x_{*}=0, \quad x_{*}=\pm \sqrt{\frac{1}{2}(1 \pm \sqrt{1+4 r})} \quad \text { (five fixed points); } \\ r>0: \quad x_{*}=0, \quad x_{*}=\pm \sqrt{\frac{1}{2}(1+\sqrt{1+4 r})} \quad \text { (three fixed points). } \end{array} \nonumber \]
La estabilidad se determina a partir de\(f^{\prime}(x)=r+3 x^{2}-5 x^{4}\). Ahora,\(f^{\prime}(0)=r\) así\(x_{*}=0\) es estable para\(r<0\) e inestable para\(r>0\). El cálculo para las otras cuatro raíces puede simplificarse señalando que\(x_{*}\) satisface\(r+x_{*}^{2}-x_{*}^{4}=0\), o\(x_{*}^{4}=r+x_{*}^{2}\). Por lo tanto,
\[\begin{aligned} f^{\prime}\left(x_{*}\right) &=r+3 x_{*}^{2}-5 x_{*}^{4} \\ &=r+3 x_{*}^{2}-5\left(r+x_{*}^{2}\right) \\ &=-4 r-2 x_{*}^{2} \\ &=-2\left(2 r+x_{*}^{2}\right) \end{aligned} \nonumber \]
Con\(x_{*}^{2}=\frac{1}{2}(1 \pm \sqrt{1+4 r})\), tenemos
\[\begin{aligned} f^{\prime}\left(x_{*}\right) &=-2\left(2 r+\frac{1}{2}(1 \pm \sqrt{1+4 r})\right) \\ &=-((1+4 r) \pm \sqrt{1+4 r}) \\ &=-\sqrt{1+4 r}(\sqrt{1+4 r} \pm 1) \end{aligned} \nonumber \]
Claramente, la raíz plus siempre es estable desde entonces\(f^{\prime}\left(x_{*}\right)<0\). La raíz menos existe solo para\(-\frac{1}{4}<r<0\) y es inestable desde entonces\(f^{\prime}\left(x_{*}\right)>0\). Resumimos la estabilidad de los diversos puntos fijos:
\[\begin{aligned} & r<-\frac{1}{4}: \quad x_{*}=0 \quad(\text { stable }) \\ & -\frac{1}{4}<r<0: \quad x_{*}=0, \quad \text { (stable) } \\ & x_{*}=\pm \sqrt{\frac{1}{2}(1+\sqrt{1+4 r})} \quad(\text { stable }) \\ & x_{*}=\pm \sqrt{\frac{1}{2}(1-\sqrt{1+4 r})} \text { (unstable); } \\ & r>0: \quad x_{*}=0 \quad \text { (unstable) } \\ & x_{*}=\pm \sqrt{\frac{1}{2}(1+\sqrt{1+4 r})} \quad \text { (stable) } . \end{aligned} \nonumber \]
El diagrama de bifurcación se muestra en la Fig. 11.5, y consiste en una bifurcación de horca subcrítica en\(r=0\) y dos bifurcaciones de nodo de silla de montar en\(r=-1 / 4\). Podemos imaginar lo que sucede a\(x\) medida que\(r\) aumenta a partir de valores negativos, suponiendo que haya algún pequeño ruido en el sistema para\(x=x(t)\) que diverja de puntos fijos inestables. Para\(r<-1 / 4\), el valor de equilibrio de\(x\) es\(x_{*}=0\). A medida que los\(r\) aumentos en el rango\(-1 / 4<r<0, x\) se mantendrán en\(x_{*}=0\). Sin embargo, una catástrofe ocurre tan pronto como\(r>0\). El punto\(x_{*}=0\) fijo se vuelve inestable y la solución saltará hacia arriba (o hacia abajo) al único punto fijo estable restante. Tal comportamiento se llama bifurcación de salto. Una catástrofe similar puede ocurrir como\(r\) disminuciones a partir de valores positivos. En este caso, el salto ocurre tan pronto como sea\(r<-1 / 4\).
Dado que el valor de equilibrio estable de\(x\) depende de si estamos aumentando o disminuyendo\(r\), decimos que el sistema exhibe histéresis. La existencia de una bifurcación de horca subcrítica puede ser muy peligrosa en aplicaciones de ingeniería, ya que un pequeño cambio en los parámetros de un problema puede resultar en un gran cambio en el estado de equilibrio. Físicamente, esto puede corresponder a un colapso de una estructura, o al fallo de un componente.
11.2.5. Aplicación: un modelo matemático de una pesquería
Ilustramos la utilidad de la teoría de la bifurcación analizando un modelo simple de pesquería. Utilizamos la ecuación logística (ver\(\S 7.4 .6\)) para modelar una población de peces en ausencia de pesca. Para modelar la pesca, asumimos que el gobierno ha establecido cuotas de pesca para que a lo sumo se pueda capturar un total de\(C\) peces por año. Suponemos que cuando la población de peces está a la capacidad de carga del medio ambiente, el pescador puede capturar casi su cuota completa. Cuando la población de peces desciende a valores más bajos, los peces pueden ser más difíciles de encontrar y la tasa de captura puede caer por debajo\(C\), eventualmente llegando a cero a medida que la población de peces disminuye. Combinando la ecuación logística junto con un modelo simple de pesca, proponemos el modelo matemático
\[\frac{d N}{d t}=r N\left(1-\frac{N}{K}\right)-\frac{C N}{A+N} \nonumber \]
donde\(N\) esta el tamaño de la poblacion de peces,\(t\)\(r\) es el tiempo, es la tasa de crecimiento potencial máxima de la poblacion de peces,\(K\) es la capacidad de carga del ambiente,\(C\) es la tasa máxima a la que los peces pueden ser capturados, y\(A\) es una satisfacción constante\(A<K\) que se utiliza para modelar la idea de que los peces se vuelven más difíciles de atrapar cuando son escasos.
No dimensionalizamos la Ecuación\ ref {11.4} usando\(x=N / K, \tau=r t, c=C / r K, \alpha=A / K\):
\[\frac{d x}{d \tau}=x(1-x)-\frac{c x}{\alpha+x} . \nonumber \]
Tenga en cuenta que\(0 \leq x \leq 1, c>0\) y\(0<\alpha<1\). Deseamos describir cualitativamente las soluciones de equilibrio de la Ecuación\ ref {11.5} y las bifurcaciones que pueden ocurrir a medida que la tasa de captura no dimensional\(c\) aumenta desde cero. Prácticamente, a un gobierno le gustaría emitir cada año una cuota de captura lo más grande posible sin afectar de manera adversa el número de peces que pueden capturarse en los años siguientes.
Los puntos fijos de la Ecuación\ ref {11.5} son\(x_{*}=0\), válidos para todos\(c\), y las soluciones a\(x^{2}-\)\((1-\alpha) x+(c-\alpha)=0\), o
\[x_{*}=\frac{1}{2}\left[(1-\alpha) \pm \sqrt{(1+\alpha)^{2}-4 c}\right] . \nonumber \]
Los puntos fijos dados por la Ecuación\ ref {11.6} son reales solo si\(c<\frac{1}{4}(1+\alpha)^{2}\). Además, la raíz menos es mayor que cero solo si\(c>\alpha\). Por lo tanto, debemos considerar tres intervalos a lo largo de los cuales existen los siguientes puntos fijos:
\[\begin{aligned} 0 \leq c \leq \alpha: & x_{*}=0, \quad x_{*}=\frac{1}{2}\left[(1-\alpha)+\sqrt{(1+\alpha)^{2}-4 c}\right] \\ \alpha<c<\frac{1}{4}(1+\alpha)^{2}: & x_{*}=0, \quad x_{*}=\frac{1}{2}\left[(1-\alpha) \pm \sqrt{(1+\alpha)^{2}-4 c}\right] \\ c>\frac{1}{4}(1+\alpha)^{2}: & x_{*}=0 . \end{aligned} \nonumber \]
La estabilidad de los puntos fijos se puede determinar con rigor analítica o gráficamente. Aquí, simplemente aplicamos la intuición biológica junto con el conocimiento de los tipos de bifurcaciones unidimensionales. Un argumento intuitivo se simplifica si consideramos\(c\) disminuir a partir de valores grandes. Cuando\(c\) es grande, es decir\(c>\frac{1}{4}(1+\alpha)^{2}\), se están capturando demasiados peces y nuestra intuición sugiere que la población de peces se extingue. Por lo tanto, en este intervalo, el único punto fijo\(x_{*}=0\) debe ser estable. Como
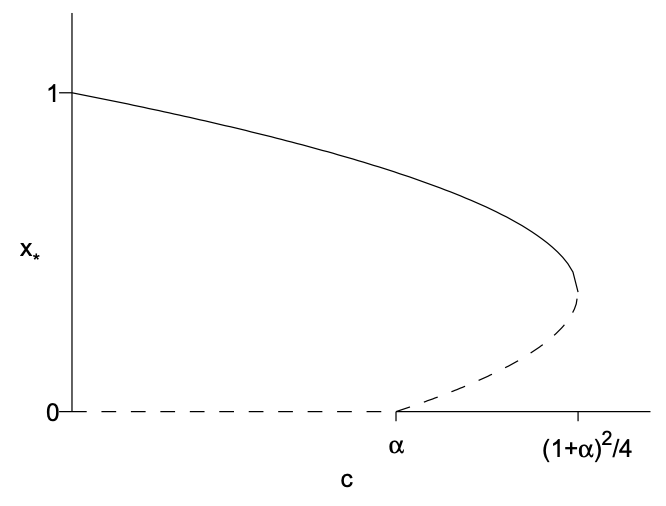
\(c\)disminuye, se produce una bifurcación al\(c=\frac{1}{4}(1+\alpha)^{2}\) introducir dos puntos fijos adicionales en\(x_{*}=(1-\alpha) / 2\). El tipo de bifurcación unidimensional en la que se crean dos puntos fijos a medida que una raíz cuadrada se vuelve real es una bifurcación de silla de montar, y uno de los puntos fijos será estable y el otro inestable. Siguiendo estos puntos fijos como\(c \rightarrow 0\), observamos que la raíz más va a uno, que es el punto fijo estable apropiado cuando no hay pesca. Por lo tanto, concluimos que la raíz más es estable y la raíz menos es inestable. A\(c\) medida que disminuye más a partir de esta bifurcación, la raíz menos choca con el punto fijo\(x_{*}=0\) en\(c=\alpha\). Esto parece ser una bifurcación transcrítica y suponiendo que se produzca un intercambio de estabilidad, debemos tener el punto fijo\(x_{*}=0\) volviéndose inestable para\(c<\alpha\). El diagrama de bifurcación resultante se muestra en la Fig. 11.6.
El propósito de los modelos matemáticos simples aplicados a problemas ecológicos complejos es ofrecer alguna visión. Aquí, hemos aprendido que la sobrepesca (en el modelo\(\left.c>\frac{1}{4}(1+\alpha)^{2}\right)\) durante un año puede potencialmente resultar en un colapso repentino de la captura de peces en los años siguientes, por lo que los gobiernos deben ser particularmente cautelosos a la hora de contemplar aumentos en las cuotas de pesca.


