7.2: Ecuaciones acopladas de primer orden

Consideramos ahora el sistema general de ecuaciones diferenciales dado por el \[\label{eq:1}\overset{.}{x}_1=ax_1+bx_2,\quad\overset{.}{x}_2=cx_1+dx_2,\]cual se puede escribir usando notación vectorial como \[\label{eq:2}\overset{.}{\mathbf{x}}=\mathbf{Ax}.\]

Antes de resolver este sistema de odas usando técnicas matriciales, primero quiero demostrar que en realidad podríamos resolver estas ecuaciones convirtiendo el sistema en una sola ecuación de segundo orden. Tomamos la derivada de la primera ecuación y usamos ambas ecuaciones para escribir\[\begin{aligned}\overset{..}{x}_1&=a\overset{.}{x}_1+b\overset{.}{x}_2 \\ &=a\overset{.}{x}_1+b(cx_1+dx_2) \\ &=a\overset{.}{x}_1+bcx_1+d(\overset{.}{x}_1-ax_1) \\ &=(a+d)\overset{.}{x}_1-(ad-bc)x_1.\end{aligned}\]

Por lo tanto, el sistema de dos ecuaciones de primer orden se convierte en la siguiente ecuación de segundo orden:

\[\overset{..}{x}_1-(a+d)\overset{.}{x}_1+(ad-bc)x_1=0.\nonumber\]

Si hubiéramos tomado la derivada de la segunda ecuación en su lugar, habríamos obtenido la ecuación idéntica para\(x_2\):

\[\overset{..}{x}_2-(a+d)\overset{.}{x}_2+(ad-bc)x_2=0.\nonumber\]

En general, un sistema de ecuaciones homogéneas lineales de\(n\) primer orden se puede convertir en una ecuación homogénea lineal de orden\(n\) -ésimo equivalente. Los métodos numéricos suelen requerir la conversión a la inversa; es decir, una conversión de una ecuación de orden\(n\) -ésimo en un sistema de ecuaciones de\(n\) primer orden.

Con el ansatz\(x_1 = e^{\lambda t}\) o\(x_2 = e^{\lambda t}\), las odas de segundo orden tienen la ecuación característica\[\lambda^2-(a+d)\lambda +(ad-bc)=0.\nonumber\]

Esto es idéntico a la ecuación característica obtenida para la matriz\(\mathbf{A}\) a partir de un análisis de valores propios.

Veremos que de hecho se\(\eqref{eq:1}\) puede resolver considerando los valores propios y vectores propios de la matriz\(\mathbf{A}\). Demostraremos la solución para tres casos separados: (i) los valores propios de\(\mathbf{A}\) son reales y hay dos vectores propios linealmente independientes; (ii) los valores propios de\(\mathbf{A}\) son conjugados complejos, y; (iii)\(\mathbf{A}\) tiene solo un vector propio linealmente independiente. Estos tres casos son análogos a los casos considerados previamente al resolver la ecuación de segundo orden de coeficiente constante lineal homogéneo.

Distintos valores propios reales

Ilustramos el método de solución con el ejemplo.

Ejemplo\(\PageIndex{1}\)

Encuentra la solución general de\(\overset{.}{x}_1=x_2+x_2,\:\overset{.}{x}_2=4x_1+x_2\).

Solución

Ver tutorial en YouTube

La ecuación a resolver puede ser reescrita en forma de matriz como\[\frac{d}{dt}\left(\begin{array}{c}x_1\\x_2\end{array}\right)=\left(\begin{array}{cc}1&1\\4&1\end{array}\right)\left(\begin{array}{c}x_1\\x_2\end{array}\right),\nonumber\] o usando notación vectorial, escrita como\(\eqref{eq:2}\). Tomamos como nuestro ansatz\(\mathbf{x}(t) = \mathbf{v}e^{\lambda t}\), donde\(\mathbf{v}\) y\(\lambda\) somos independientes de\(t\). Al sustituir en\(\eqref{eq:2}\), obtenemos\[\lambda\mathbf{v}e^{\lambda t}=\mathbf{Av}e^{\lambda t};\nonumber\] y al cancelar lo exponencial, obtenemos el problema del valor propio \[\label{eq:3}\mathbf{Av}=\lambda\mathbf{v}.\]

Al encontrar la ecuación característica usando (7.1.8), tenemos\[\begin{aligned}0&=\det (\mathbf{A}-\lambda\mathbf{I}) \\ &=\lambda^2-2\lambda -3 \\ &=(\lambda -3)(\lambda +1).\end{aligned}\]

Por lo tanto, los dos valores propios son\(\lambda_1=3\) y\(\lambda_2=-1\).

Para determinar los vectores propios correspondientes, sustituimos los autovalores sucesivamente en \[\label{eq:4}(\mathbf{A}-\lambda\mathbf{I})\mathbf{v}=0.\]

Escribiremos los vectores propios correspondientes\(\mathbf{v_1}\) y\(\mathbf{v_2}\) usando la notación matricial\[\left(\begin{array}{cc}\mathbf{v_1}&\mathbf{v_2}\end{array}\right)=\left(\begin{array}{cc}v_{11}&v_{12} \\ v_{21}&v_{22}\end{array}\right),\nonumber\] donde los componentes de\(\mathbf{v_1}\) y\(\mathbf{v_2}\) se escriben con subíndices correspondientes a la primera y segunda columnas de una\(2\times 2\) matriz.

Para\(\lambda_1 = 3\), y autovector desconocido\(\mathbf{v_1}\), tenemos de\(\eqref{eq:4}\)\[\begin{aligned}-2v_{11}+v_{21}&=0, \\ 4v_{11}-2v_{21}&=0.\end{aligned}\]

Claramente, la segunda ecuación es solo la primera ecuación multiplicada por\(−2\), por lo que sólo una ecuación es linealmente independiente. Esto siempre será cierto, así que para el\(2\times 2\) caso solo necesitamos considerar la primera fila de la matriz. Por lo tanto, el primer vector propio satisface\(v_{21} = 2v_{11}\). Recordemos que un vector propio solo es único hasta la multiplicación por una constante: por lo tanto, podemos tomarlo\(v_{11} = 1\) por conveniencia.

Para\(\lambda_2 = −1\), y eigenvector\(\mathbf{v_2} = (v_{12}, v_{22})^T\), tenemos de\(\eqref{eq:4}\)\[2v_{12}+v_{22}=0,\nonumber\] para que\(v_{22}=-2v_{12}\). Aquí, tomamos\(v_{12}=1\).

Por lo tanto, nuestros valores propios y vectores propios están dados por\[\lambda_1=3,\:\mathbf{v_1}=\left(\begin{array}{c}1\\2\end{array}\right);\quad\lambda_2=-1,\:\mathbf{v_2}=\left(\begin{array}{c}1\\-2\end{array}\right).\nonumber\]

Un nodo puede estar atrayendo o repeliendo dependiendo de si los valores propios son negativos (como es el caso aquí) o positivos. Observe que las trayectorias colapsan sobre el\(\mathbf{v_2}\) autovector ya que\(\lambda_1 < \lambda_2 < 0\) y la decadencia es más rápida a lo largo de la\(\mathbf{v_1}\) dirección.

Distintos valores propios de complejo-conjugado

Ejemplo\(\PageIndex{2}\)

Encuentra la solución general de\(\overset{.}{x}_1=-\frac{1}{2}x_1+x_2 ,\:\overset{.}{x}_2=-x_1-\frac{1}{2}x_2\).

Solución

Ver tutorial en YouTube

Las ecuaciones en forma de matriz son\[\frac{d}{dt}\left(\begin{array}{c}x_1 \\ x_2\end{array}\right)=\left(\begin{array}{cc}-\frac{1}{2}&1 \\ -1&-\frac{1}{2}\end{array}\right)\left(\begin{array}{c}x_1 \\ x_2\end{array}\right).\nonumber\]

El ansatz\(\mathbf{x} = \mathbf{v}e^{\lambda t}\) lleva a la ecuación\[\begin{aligned}0&=\det (\mathbf{A}-\lambda\mathbf{I}) \\ &=\lambda^2+\lambda +\frac{5}{4}.\end{aligned}\]

Por lo tanto,\(\lambda = −1/2 ± i\); y observamos que los valores propios ocurren como un par conjugado complejo. Denotaremos los dos valores propios como\[\lambda =-\frac{1}{2}+i\quad\text{and}\quad\overline{\lambda}=-\frac{1}{2}-i.\nonumber\]

Ahora, para\(\mathbf{A}\) una matriz real, si\(\mathbf{Av} = \lambda\mathbf{v}\), entonces\(\mathbf{A}\mathbf{\overline{v}}=\overline{\lambda}\mathbf{\overline{v}}\). Por lo tanto, los vectores propios también ocurren como un par conjugado complejo. El vector propio\(\mathbf{v}\) asociado con el valor propio\(\lambda\) satisface\(−iv_1 + v_2 = 0\), y normalizando con\(v_1 = 1\), tenemos\[\mathbf{v}=\left(\begin{array}{c}1 \\ i\end{array}\right).\nonumber\]

Por lo tanto, hemos determinado dos soluciones complejas independientes a la oda, es decir,\[\mathbf{v}e^{\lambda t}\quad\text{and}\quad\mathbf{\overline{v}}e^{\overline{\lambda}t},\nonumber\] y podemos formar una combinación lineal de estas dos soluciones complejas para construir dos soluciones reales independientes. Es decir, si las funciones complejas\(z(t)\) y\(\overline{z}(t)\) se escriben como\[z(t)=\text{Re }\{z(t)\}+i\text{ Im }\{z(t)\},\quad\overline{z}(t)=\text{Re }\{z(t)\}-i\text{ Im }\{z(t)\},\nonumber\] entonces dos funciones reales se pueden construir a partir de las siguientes combinaciones lineales de\(z\) y\(\overline{z}\):

\[\frac{z+\overline{z}}{2}=\text{Re }\{z(t)\}\quad\text{and}\quad\frac{z-\overline{z}}{2i}=\text{Im }\{z(t)\}.\nonumber\]

Así, las dos funciones vectoriales reales que se pueden construir a partir de nuestras dos funciones vectoriales complejas son\[\begin{aligned}\text{Re }\{\mathbf{v}e^{\lambda t}\}&=\text{Re }\left\{\left(\begin{array}{c}1 \\ i\end{array}\right)e^{(-\frac{1}{2}+i)t}\right\} \\ &=e^{-\frac{1}{2}t}\text{Re }\left\{\left(\begin{array}{c}1\\i\end{array}\right)(\cos t+i\sin t)\right\} \\ &=e^{-\frac{1}{2}t}\left(\begin{array}{c}\cos t \\ -\sin t\end{array}\right);\end{aligned}\]

Figura\(\PageIndex{1}\): Retrato de fase con valores propios conjugados complejos.

y\[\begin{aligned}\text{Im }\{\mathbf{v}e^{\lambda t}\}&=e^{-\frac{1}{2}t}\text{Im }\left\{\left(\begin{array}{c}1\\i\end{array}\right)(\cos t+i\sin t)\right\} \\ &=e^{-\frac{1}{2}t}\left(\begin{array}{c}\sin t\\ \cos t\end{array}\right).\end{aligned}\]

Tomando una superposición lineal de estas dos soluciones reales produce la solución general a la oda, dada por\[\mathbf{x}=e^{-\frac{1}{2}t}\left(A\left(\begin{array}{c}\cos t \\-\sin t\end{array}\right)+B\left(\begin{array}{c}\sin t\\ \cos t\end{array}\right)\right).\nonumber\]

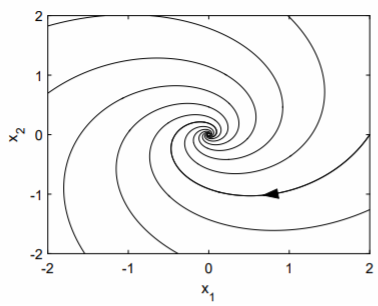
El retrato de fase correspondiente se muestra en la Fig. \(\PageIndex{1}\). Decimos que el origen es un punto espiral. Si la parte real del valor propio complejo es negativa, como es el caso aquí, entonces las soluciones entran en espiral hacia el origen. Si la parte real del valor propio es positiva, entonces las soluciones salen en espiral del origen.

La dirección de la espiral, aquí, es en sentido horario, se puede determinar fácilmente. Si examinamos la oda con\(x_1 = 0\) y\(x_2 = 1\), vemos que\(\overset{.}{x}_1 = 1\) y\(\overset{.}{x}_2 = −1/2\). La trayectoria en el punto\((0, 1)\) se mueve hacia la derecha y hacia abajo, y esto solo es posible si la espiral está en el sentido de las agujas del reloj. Una trayectoria en sentido antihorario se estaría moviendo hacia la izquierda y hacia abajo.

Valores propios repetidos con un vector propio

Ejemplo\(\PageIndex{3}\)

Encuentra la solución general de\(\overset{.}{x}_1=x_1-x_2,\:\overset{.}{x}_2=x_1+3x_2\).

Solución

Ver tutorial en YouTube

Las ecuaciones en forma de matriz son \[\label{eq:5}\frac{d}{dt}\left(\begin{array}{c}x_1 \\ x_2\end{array}\right)=\left(\begin{array}{cc}1&-1 \\ 1&3\end{array}\right)\left(\begin{array}{c}x_1 \\ x_2\end{array}\right).\]

El ansatz\(\mathbf{x} = \mathbf{v}e^{\lambda t}\) conduce a la ecuación característica\[\begin{aligned}0&=\det (\mathbf{A}-\lambda\mathbf{I}) \\ &=\lambda^2-4\lambda +4 \\ &=(\lambda -2)^2.\end{aligned}\]

Por lo tanto,\(\lambda = 2\) es un valor propio repetido. El vector propio asociado se encuentra de\(−v_1 − v_2 = 0\), o\(v_2 = −v_1\); y normalizando con\(v_1 = 1\), tenemos\[\lambda =2,\quad\mathbf{v}=\left(\begin{array}{c}1\\-1\end{array}\right).\nonumber\]

Hemos encontrado así una única solución a la oda, dada por\[\mathbf{x_1}(t)=c_1\left(\begin{array}{c}1\\-1\end{array}\right)e^{2t},\nonumber\] y necesitamos encontrar la segunda solución faltante para poder satisfacer las condiciones iniciales. Un ansatz de\(t\) veces la primera solución es tentadora, pero fallará. Aquí, haremos trampa y encontraremos la segunda solución faltante resolviendo la ecuación diferencial equivalente de segundo orden, homogénea y de coeficiente constante.

Ya sabemos que esta ecuación diferencial de segundo orden para\(x_1(t)\) tiene una ecuación característica con un valor propio degenerado dado por\(\lambda = 2\). Por lo tanto, la solución general para\(x_1\) viene dada por\[x_1(t)=(c_1+tc_2)e^{2t}.\nonumber\]

Dado que a partir de la primera ecuación diferencial,\(x_2 = x_1 − \overset{.}{x}_1\), calculamos de\[\overset{.}{x}_1=(2c_1+(1+2t)c_2)e^{2t},\nonumber\] manera que\[\begin{aligned}x_2&=x_1-\overset{.}{x}_1 \\ &=(c_1+tc_2)e^{2t}-(2c_1+(1+2t)c_2)e^{2t} \\ &=-c_1e^{2t}+c_2(-1-t)e^{2t}.\end{aligned}\]

Combinando nuestros resultados para\(x_1\) y\(x_2\), por lo tanto, hemos encontrado\[\left(\begin{array}{c}x_1 \\ x_2\end{array}\right)=c_1\left(\begin{array}{c}1\\-1\end{array}\right)e^{2t}+c_2\left[\left(\begin{array}{c}0\\-1\end{array}\right)+\left(\begin{array}{c}1\\-1\end{array}\right)t\right]e^{2t}.\nonumber\]

Nuestra solución linealmente independiente que falta está así determinada a \[\label{eq:6}\mathbf{x}(t)=c_2\left[\left(\begin{array}{c}0\\-1\end{array}\right)+\left(\begin{array}{c}1\\-1\end{array}\right)t\right]e^{2t}.\]

El segundo término de\(\eqref{eq:6}\) es solo\(t\) veces la primera solución; sin embargo, esto no es suficiente. En efecto, el ansatz correcto para encontrar la segunda solución directamente viene dado por \[\label{eq:7}\mathbf{x}=(\mathbf{w}+t\mathbf{v})e^{\lambda t},\]

Figura\(\PageIndex{2}\): Retrato de fase con un solo vector propio.

donde\(\lambda\) y\(\mathbf{v}\) es el valor propio y el vector propio de la primera solución, y\(\mathbf{w}\) es un vector desconocido por determinar. Para ilustrar este método directo, sustituimos\(\eqref{eq:7}\) en\(\mathbf{\overset{.}{x}} = \mathbf{Ax}\), asumiendo\(\mathbf{Av} = \lambda\mathbf{v}\). Cancelando lo exponencial, obtenemos\[\mathbf{v}+\lambda (\mathbf{w}+t\mathbf{v})=\mathbf{Aw}+\lambda t\mathbf{v}.\nonumber\]

Cancelación adicional del término común\(\lambda t\mathbf{v}\) y reescritura de rendimientos \[\label{eq:8}(\mathbf{A}-\lambda\mathbf{I})\mathbf{w}=\mathbf{v}.\]

Si solo\(\mathbf{A}\) tiene un único vector propio linealmente independiente\(\mathbf{v}\), entonces se\(\eqref{eq:8}\) puede resolver para\(\mathbf{w}\) (de lo contrario, no puede). Utilizando\(\mathbf{A}\),\(\lambda\) y\(\mathbf{v}\) de nuestro ejemplo actual,\(\eqref{eq:8}\) está el sistema de ecuaciones dado por\[\left(\begin{array}{cc}-1&-1 \\ 1&1\end{array}\right)\left(\begin{array}{c}w_1\\w_2\end{array}\right)=\left(\begin{array}{c}1\\-1\end{array}\right).\nonumber\]

La primera y la segunda ecuación son las mismas, así que eso\(w_2 = −(w_1 + 1)\). Por lo tanto,\[\begin{aligned}\mathbf{w}&=\left(\begin{array}{c}w_1 \\ -(w_1+1)\end{array}\right) \\ &=w_1\left(\begin{array}{c}1\\-1\end{array}\right)+\left(\begin{array}{c}0\\-1\end{array}\right).\end{aligned}\]

Observe que el primer término repite la primera solución encontrada, es decir, una constante multiplicada por el vector propio, y el segundo término es nuevo. Por lo tanto tomamos\(w_1 = 0\) y obtenemos\[\mathbf{w}=\left(\begin{array}{c}0\\-1\end{array}\right),\nonumber\] como antes.

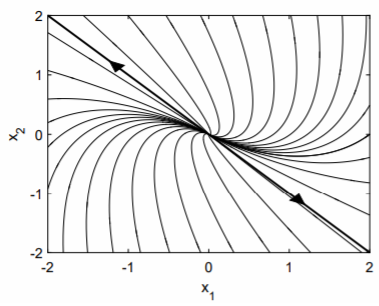
El retrato de fase para esta oda se muestra en la Fig. \(\PageIndex{2}\). La línea oscura es el único vector propio\(\mathbf{v}\) de la matriz\(\mathbf{A}\). Cuando solo hay un único vector propio, el origen se denomina nodo incorrecto.