6.1: Conjunto de problemas

Última actualización
Guardar como PDF

Page ID: 113593

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

EJERCIO$\PageIndex{1}$

Considere$C^{r}$ el$r \ge 1$ campo vectorial autónomo en$\mathbb{R}^2$:

$\dot{x} = f(x)$,

con flujo

$\phi_{t}(\cdot)$,

y let$x = \bar{x}$ denotar un punto de equilibrio tipo silla hiperbólica para este campo vectorial. Denotamos los colectores locales estables e inestables de este punto de equilibrio por:

$W_{loc}^{s}(\bar{x})$,$W_{loc}^{u}(\bar{x})$,

respectivamente. Los colectores globales estables e inestables de$\bar{x}$ se definen por:

$W^{s}(\bar{x}) \equiv \cup_{t \le 0} \phi_{t} (W_{loc}^{s}(\bar{x}))$,

$W^{u}(\bar{x}) \equiv \cup_{t \ge 0} \phi_{t} (W_{loc}^{s}(\bar{x}))$,

(a) Demostrar que$W^{s}(\bar{x})$ y$W^{u}(\bar{x})$ son conjunto invariante.

(b) Supongamos que$p \in W^{s}(\bar{x})$, mostrar que$\phi_{t}(p) \rightarrow \bar{x}$ a una tasa exponencial como$t \rightarrow \infty$.

(c) Supongamos que$p \in W^{u}(\bar{x})$, mostrar que$\phi_{t}(p) \rightarrow \bar{x}$ a un ritmo exponencial como$t \rightarrow -\infty$.

EJERCIO$\PageIndex{2}$

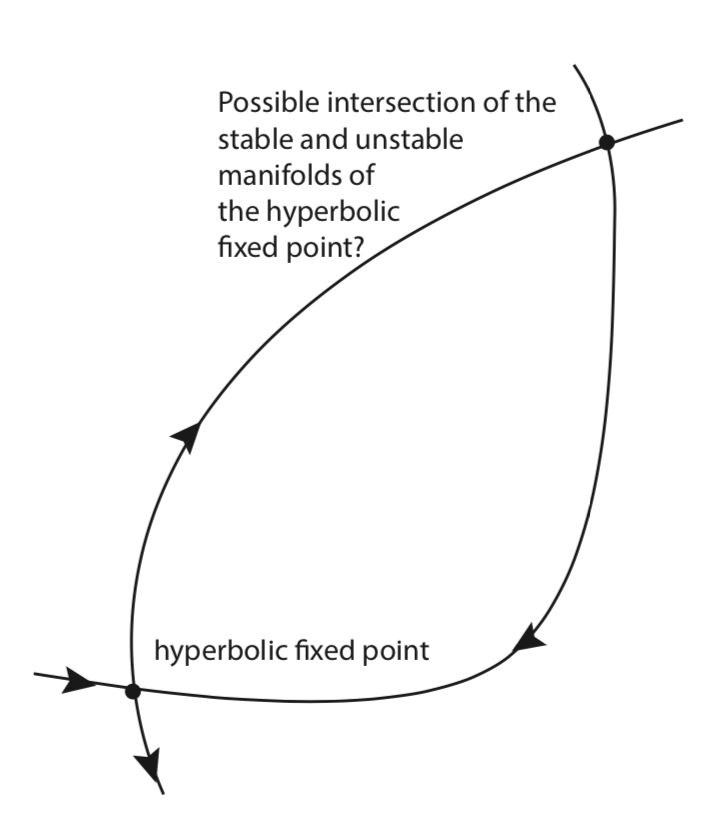
Considere el$C^{r}, r \ge 1$ campo vectorial autónomo al$\mathbb{R}^2$ tener un punto de sillín hiperbólico. ¿Pueden sus colectores estables e inestables cruzarse en un punto aislado (que no es un punto fijo del campo vectorial) como se muestra en la figura 2?

$Screen Shot 2019-09-26 a las 12.45.53 PM.png$

EJERCIO$\PageIndex{3}$

Considere el siguiente campo vectorial autónomo en el plano:

$\dot{x} = \alpha x$,

\[\dot{y} = \beta y + \gamma x^{n+1}, \label{6.42}\]

donde$\alpha < 0$,$\beta > 0$,$\gamma$ es un número real, y n es un entero positivo.

Mostrar que el origen es un punto de sillín hiperbólico.
Calcula y bosqueja los subespacios estables e inestables del origen.
Mostrar que los subespacios estables e inestables son invariantes bajo la dinámica linealizada.
Mostrar el flujo generado por este campo vectorial viene dado por:
$x(t, x_{0}) = x_{0}e^{\alpha t}$,

$y(t, x_{0}, y_{0}) = e^{\beta t}(y_{0} - \frac{\gamma x_{0}^{n+1}}{\alpha (n+1) - \beta}) + (\frac{\gamma x_{0}^{n+1}}{\alpha (n+1) - \beta}) e^{\alpha (n+1)t}$
Calcula los colectores globales estables e inestables del origen a partir del flujo.
Demuestre que los colectores globales estables e inestables que ha calculado son invariantes.
Esboce los colectores globales estables e inestables y discuta cómo dependen de g y n.

EJERCIO$\PageIndex{4}$

Supongamos que$\dot{x} = f(x), x \in \mathbb{R}^n$ es un campo$C^r$ vectorial que tiene un punto fijo hiperbólico$x = x_{0}$,, con una órbita homoclínica. Describir la órbita homoclínica en términos de los colectores estables e inestables de$x_{0}$.

EJERCIO$\PageIndex{5}$

Supongamos que$\dot{x} = f(x), x \in \mathbb{R}^n$ es un campo$C^r$ vectorial que tiene puntos fijos hiperbólicos,$x = x_{0}$ y$x_{1}$, con una órbita heteroclínica conectando$x_{0}$ y$x_{1}$. Describir la órbita heteroclínica en términos de los colectores estables e inestables de$x_{0}$ y$x_{1}$.