7.1: Método de Lyapunov y principio de invarianza LaSalle

A continuación aprenderemos un método para determinar la estabilidad de los equilibrios que se puede aplicar cuando la información de estabilidad obtenida de la linealización de la ODE no sea suficiente para determinar la información de estabilidad para la ODE no lineal. El libro de LaSalle es un excelente complemento a esta conferencia. Este es el método de Lyapunov (o el segundo método de Lyapunov, o el método de las funciones de Lyapunov). Comenzamos describiendo el framework para el método en la configuración que usaremos.

Consideramos una ODE\(C^{r}, r \ge 1\) autónoma general

\[\dot{x} = f(x), x \in \mathbb{R}, \label{7.1}\]

que tiene un punto de equilibrio en\(x = \bar{x}\), es decir,

\[f(\bar{x}) = 0, \label{7.2}\]

Para una función de valor escalar definida en\(\mathbb{R}^n\)

\(V: \mathbb{R}^n \rightarrow \mathbb{R}\),

\[x \mapsto V(x), \label{7.3}\]

definimos la derivada de la Ecuación\ ref {7.3} a lo largo de las trayectorias de la Ecuación\ ref {7.1} por:

\(\frac{d}{dt} V(x) = \dot{V}(x) = \nabla V(x) \cdot \dot{x}\),

\[\nabla V(x) \cdot f(x), \label{7.4}\]

Ahora podemos exponer el teorema de Lyapunov sobre la estabilidad del punto de equilibrio\(x = \bar{x}\).

Teorema 1

Considere el siguiente campo vectorial\(C^{r} (r \ge 1)\) autónomo en\(\mathbb{R}^n\):

\[\dot{x} = f(x), x \in \mathbb{R}^n, \label{7.5}\].

Dejar\(x = \bar{x}\) ser un punto fijo de la Ecuación\ ref {7.5} y dejar de\(V : U \rightarrow \mathbb{R}\) ser una\(C^{1}\) función definida en alguna vecindad U de\(\bar{x}\) tal manera que:

1. \(V(\bar{x})=0\)y\(V(x) > 0\) si\(x \ne \bar{x}\).
2. \(V(\dot{x}) \le 0\)en\(U-{\bar{x}}\)

Entonces\(\bar{x}\) es Lyapunov estable. Además, si

\(\dot{V}(x) < 0\)en\(U-{\bar{x}}\)

entonces\(\bar{x}\) es asintóticamente estable.

La función\(V(x)\) se conoce como una función de Lyapunov. Consideramos ahora un ejemplo.

Ejemplo\(\PageIndex{17}\)

Considera esta función

\(\dot{x} = y\),

\[\dot{y} = -x-\epsilon x^{2}y, (x, y) \in \mathbb{R}^2, \label{7.6}\]

donde\(\epsilon\) es un parámetro. Es claro que\((x, y) = (0, 0)\) es un punto de equilibrio de la Ecuación\ ref {7.6} y queremos determinar la naturaleza de su estabilidad.

Comenzamos linealizando la Ecuación\ ref {7.6} sobre este punto de equilibrio. La matriz asociada a esta linealización viene dada por:

\[A = \begin{pmatrix} {0}&{1}\\ {-1}&{0} \end{pmatrix}, \label{7.7}\]

y sus valores propios son\(\pm i\). De ahí que el origen no sea hiperbólico y por lo tanto la información proporcionada por la linealización de (7.6) about (x, y) = (0, 0) no proporciona información sobre la estabilidad de (x, y) = (0, 0) para el sistema no lineal (Ecuación\ ref {7.6}).

Por lo tanto intentaremos aplicar el método de Lyapunov para determinar la estabilidad del origen.

Tomamos como función Lyapunov:

\[V(x, y) = \frac{1}{2}(x^2+y^2). \label{7.8}\]

Tenga en cuenta que V (0,0) = 0 y V (x, y) > 0 en cualquier vecindario del origen.

Además, contamos con:

\[\begin{align*} \dot{V}(x,y) &= \frac{\partial V}{\partial x} \dot{x}+\frac{\partial V}{\partial y} \dot{y} \\[4pt] &= xy + y(-x-\epsilon x^{2}y) \\[4pt] &= -\epsilon x^{2}y^2 \end{align*}\]

\[\le 0, \text{for} \epsilon > 0. \label{7.9}\]

De ahí que del Teorema 1 se deduce que el origen es Lyapunov estable.

A continuación introduciremos el principio de invarianza LaSalle. En lugar de centrarse en la cuestión particular de la estabilidad de una solución de equilibrio como en el método de Lyapunov, el principio de invarianza LaSalle da condiciones que describen el comportamiento como\(t \rightarrow \infty\) de todas las soluciones de una ODE autónoma.

Comenzamos con una ODE autónoma definida sobre\(\mathbb{R}^n\):

\[\dot{x} = f(x), x \in \mathbb{R}^n, \label{7.10}\]

donde f (x) es\(C^r\),\((r \ge 1)\). Dejar\(\phi_{t}(\cdot)\) denotar el flujo generado por la Ecuación\ ref {7.10} y dejar\(\mathcal{M} \subset \mathbb{R}^n\) denotar un conjunto invariante positivo que es compacto (es decir, cerrado y acotado en este ajuste). Supongamos que tenemos una función de valor escalar

\[V : \mathbb{R}^n \rightarrow \mathbb{R}, \label{7.11}\]

de tal manera que

\[\dot{V}(x) \le 0\, \text{in}\, \mathcal{M}, \label{7.12}\]

(Obsérvese el “menor o igual a” en esta desigualdad.)

Let

\[E = \{x \in \mathcal{M}|\dot{V}(x) = 0\}, \label{7.13}\]

y

\[M = \{\text{the union of all trajectories that start in E and remain in E for all} t \ge 0\} \label{7.14}\]

Ahora podemos afirmar el principio de invarianza de LaSalle.

Teorema 2: Principio de Invarianza de LaSalle

Para todos\(x \in \mathcal{M}\),\(\phi_{t}(x) \rightarrow M\) como\(t \rightarrow \infty\).

Consideraremos ahora un ejemplo.

Ejemplo\(\PageIndex{18}\)

Considere el siguiente campo vectorial en\(\mathbb{R}^2: \dot{x} = y\),

\(\dot{x} = y\),

\[\dot{y} = x-x^3-\delta y, (x, y) \in \mathbb{R}^2, \delta > 0. \label{7.15}\]

Este campo vectorial tiene tres puntos de equilibrio: un punto de sillín en (x, y) = (0, 0) y dos sumideros en\((x, y) = (\pm 1, 0)\).

Considera la función

\[V(x,y) = \frac{y^2}{2}-\frac{x^2}{2}+\frac{x^4}{4}, \label{7.16}\]

y sus conjuntos de niveles:

\[V(x, y) = C. \nonumber\]

Calculamos la derivada de V a lo largo de trayectorias de (7.15):

\(\dot{V}(x,y) = \frac{\partial V}{\partial x} \dot{x}+\frac{\partial V}{\partial y} \dot{y},\)

\(= (-x+x^3)y+y(x-x^3-\delta y)\).

\[= -\delta y^2, \label{7.17}\]

de lo que se deduce que

\(\dot{V}(x,y) \le 0\)encendido\(V(x,y) = C\).

Por lo tanto, para C suficientemente grande, el conjunto de niveles correspondiente de V limita un conjunto compacto invariante positivo,\(\mathcal{M}\), que contiene los tres puntos de equilibrio de la Ecuación\ ref {7.15}.

A continuación determinamos la naturaleza del conjunto

\[E = \{(x, y) \in \mathcal{M}|\dot{V}(x, y) = 0\}. \label{7.18}\]

Usando la ecuación\ ref {7.17} vemos que:

\[E = \{(x,y) \in \mathcal{M}|y = 0 \cap \mathcal{M}\}. \label{7.19}\]

Los únicos puntos en E que permanecen en E para siempre son:

\[M = \{(\pm 1, 0), (0, 0)\}. \label{7.20}\]

Por lo tanto se deduce del Teorema 2 que dada cualquier condición inicial en\(\mathcal{M}\), la trayectoria que comienza en esa condición inicial se acerca a uno de los tres puntos de equilibrio como\(t \rightarrow \infty\).

Campos Vectoriales Autónomos en el Plano; Criterio de Bendixson y Teorema del Índice

Ahora consideraremos algunos resultados útiles que se aplican a los campos vectoriales en el plano.

Primero consideraremos un criterio simple, y fácil de aplicar, que descarta la existencia de órbitas periódicas para campos vectoriales autónomos en el plano (por ejemplo, no es válido para campos vectoriales en los dos toros).

Consideramos un campo\(C^{r}, r \ge 1\) vectorial en el plano de la siguiente forma:

\(\dot{x} = f(x, y)\),

\[\dot{y} = g(x, y), (x, y) \in \mathbb{R}^2 \label{7.21}\]

El siguiente criterio debido a Bendixson proporciona una condición simple, computable que descarta la existencia de órbitas periódicas en ciertas regiones de\(\mathbb{R}^2\).

Teorema 3: Critterión de Bendixson

Si en una región simplemente conectada\(D \subset \mathbb{R}^2\) la expresión

\[\frac{\partial f}{\partial x} (x, y) + \frac{\partial g}{\partial y} (x, y), \label{7.22}\]

no es idénticamente cero y no cambia de signo entonces (7.21) no tiene órbitas periódicas que se encuentran enteramente en D.

Ejemplo\(\PageIndex{19}\)

Consideramos el siguiente campo vectorial autónomo no lineal en el plano:

\(\dot{x} = y \equiv f(x,y)\),

\[\dot{y} = x-x^3-\delta y \equiv g(x, y), (x, y) \in \mathbb{R}^2, d > 0. \label{7.23}\]

Computación (7.22) da:

\[\frac{\partial f}{\partial x} + \frac{\partial g}{\partial y} = -\delta, \label{7.24}\]

Por lo tanto este campo vectorial no tiene órbitas periódicas para\(\delta \ne 0\).

Ejemplo\(\PageIndex{20}\)

Consideramos el siguiente campo vectorial autónomo lineal en el plano:

\(\dot{x} = ax+by \equiv f(x, y)\),

\[\dot{y} = cx+dy \equiv g(x, y), (x, y) \in \mathbb{R}^2, a, b, c, d \in \mathbb{R} \label{7.25}\]

Computación (7.22) da:

\[\frac{\partial f}{\partial x} + \frac{\partial g}{\partial y} = a+d, \label{7.26}\]

Por lo tanto para\(a + d \ne 0\) este campo vectorial no tiene órbitas periódicas.

A continuación consideraremos el teorema del índice. Si existen órbitas periódicas, proporciona condiciones sobre el número de puntos fijos, y su estabilidad, que están contenidos en la región delimitada por la órbita periódica.

Teorema 4: teorema del índice

Dentro de cualquier órbita periódica debe haber al menos un punto fijo. Si solo hay uno, entonces debe ser un fregadero, fuente o centro. Si todos los puntos fijos dentro de la órbita periódica son hiperbólicos, entonces debe haber un número impar, 2n + 1, de los cuales n son sillas de montar, y n + 1 son sumideros o fuentes.

Ejemplo\(\PageIndex{21}\)

Consideramos el siguiente campo vectorial autónomo no lineal en el plano:

\(\dot{x} = y \equiv f(x, y)\),

\[\dot{y} = x-x^3-\delta y+x^{2}y \equiv g(x, y), (x, y) \in \mathbb{R}^2, \label{7.27}\]

donde\(\delta > 0\). Los puntos de equilibrio vienen dados por:

(x, y) = (0, 0),\((\pm 1, 0)\).

El jacobiano del campo vectorial, denotado por A, viene dado por:

\[A = \begin{pmatrix} {0}&{1}\\ {1-3x^2+2xy}&{-\delta+x^2} \end{pmatrix}, \label{7.28}\]

Usando la expresión general para los valores propios de una\(2 \times 2\) matriz A:

\(\lambda_{1,2} = \frac{tr A}{2} \pm \frac{1}{2} \sqrt{(tr A)^{2}-4det A}\),

obtenemos la siguiente expresión para los valores propios del jacobiano

\[\lambda_{1,2} = \frac{-\delta+x^2}{2} \pm \frac{1}{2} \sqrt{(-\delta+x^2)^2+4(1-3x^2+2xy)} \label{7.29}\]

Si sustituimos las ubicaciones de los equilibrios en esta expresión obtenemos los siguientes valores para los valores propios del jacobiano del campo vectorial evaluado en los equilibrios respectivos:

\[(0, 0) \lambda_{1,2} = -\frac{\delta}{2} \pm \frac{1}{2} \sqrt{\delta^2+4} \label{7.30}\]

\[(\pm 1, 0) \lambda_{1,2} = \frac{-\delta+1}{2} \pm \frac{1}{2} \sqrt{(-\delta+1)^2-8} \label{7.31}\]

De estas expresiones concluimos que (0, 0) es una silla de montar para todos los valores de\(\delta\) y\((\pm 1, 0)\) son

fregaderos para\(\delta > 1\)

centros para\(\delta = 1\)

fuentes para\(0 < \delta < 1\)

Ahora usaremos el criterio de Bendixson y el teorema del índice para determinar regiones en el plano de fase donde puedan existir órbitas periódicas. Para este ejemplo (7.22) viene dado por:

\[-\delta+x^2. \label{7.33}\]

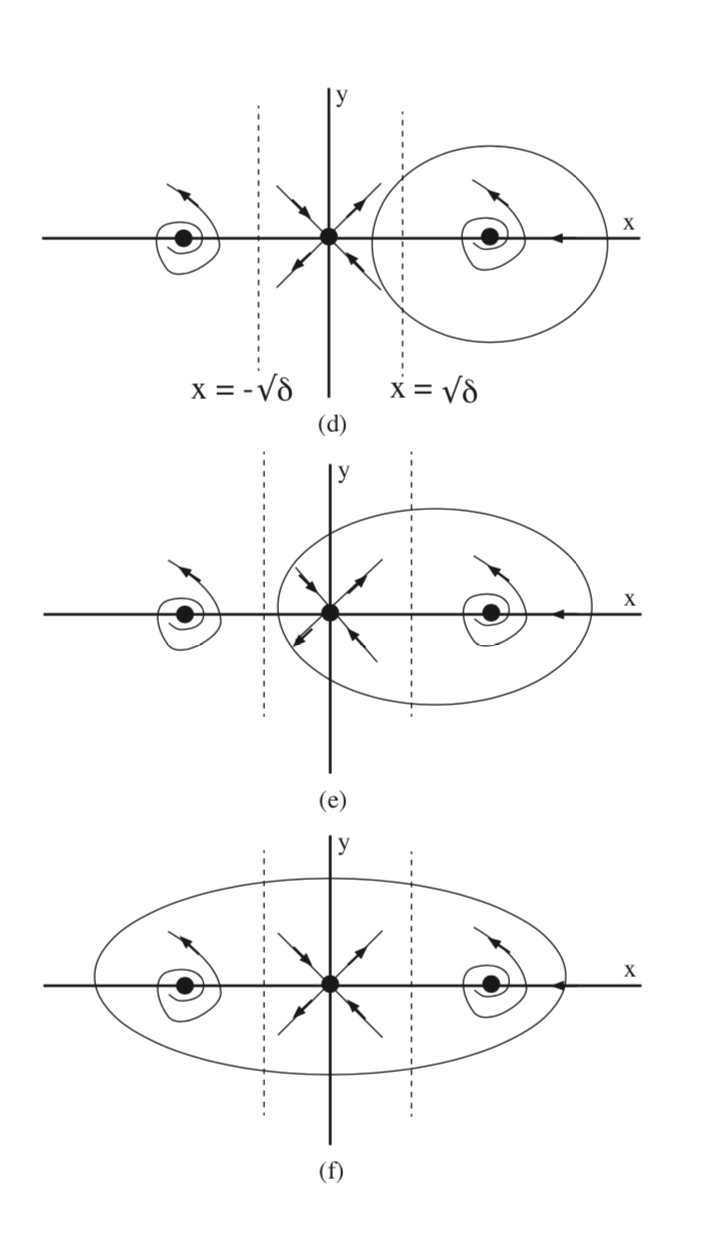
De ahí que las dos líneas verticales\(x = -\sqrt{\delta}\) y\(x = \sqrt{\delta}\) dividan el plano de fase en tres regiones donde las órbitas periódicas no pueden existir enteramente en una de estas regiones (o de lo contrario se violaría el criterio de Bendixson). Hay dos casos a considerar para la ubicación de estas líneas verticales con respecto a los equilibrios:\(\delta > 1\) y\(0 < \delta < 1\).

En la Fig. 7.1 mostramos tres posibilidades (no agotan todos los casos posibles) para la existencia de órbitas periódicas que satisfagan el criterio de Bendixson en el caso\(\delta > 1\). Sin embargo, (b) no es posible porque viola el teorema del índice.

Figura 7.1: El caso\(\delta > 1\). Posibilidades de órbitas periódicas que satisfagan el criterio de Bendixson. Sin embargo, (b) no es posible porque viola el teorema del índice.

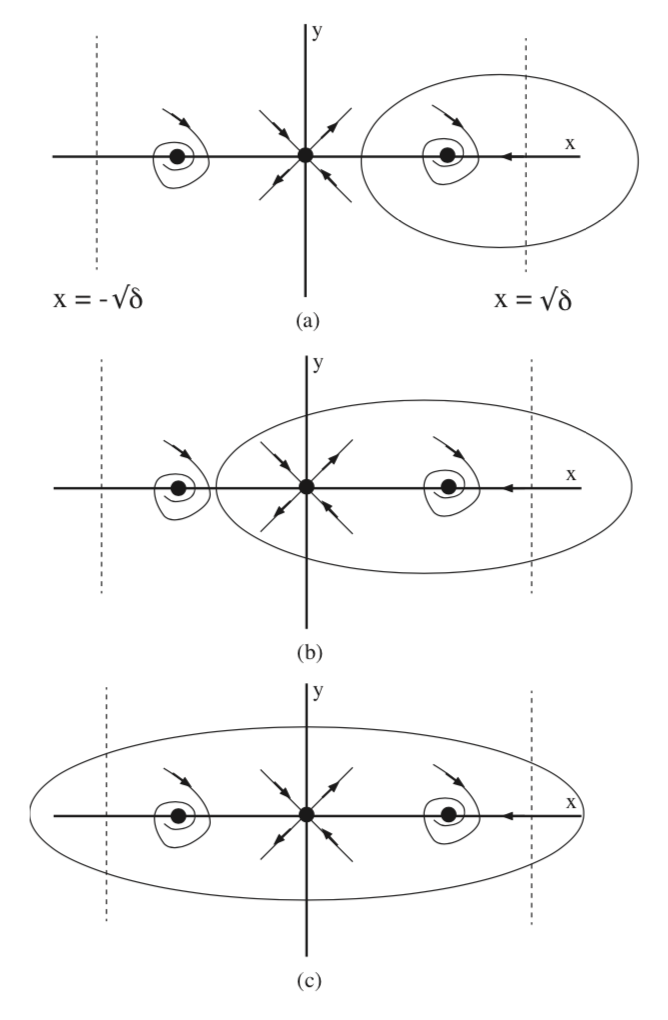
En la Fig. 7.2 mostramos tres posibilidades (no agotan todos los casos posibles) para la existencia de órbitas periódicas que satisfagan el criterio de Bendixson en el caso\(0 < \delta < 1\). Sin embargo, (e) no es posible porque viola el teorema del índice.

Figura 7.2: El caso\(0 < \delta < 1\). Posibilidades de órbitas periódicas que satisfagan el criterio de Bendixson. Sin embargo, (e) no es posible porque viola el teorema del índice.