8.1: Bifurcación de Equilibrios I
- Page ID
- 113578
Ahora vamos a estudiar el tema de la bifurcación de equilibrios de campos vectoriales autónomos, o '¿qué sucede cuando un punto de equilibrio pierde hiperbolicidad ya que un parámetro es variado?” Estudiaremos esta pregunta a través de una serie de ejemplos, y luego consideraremos lo que nos enseñan los ejemplos sobre la ''situación general” (y cuál podría ser esta).
Ejemplo\(\PageIndex{22}\): The Saddle-Node Bifurcation
Considere el siguiente campo vectorial autónomo no lineal en\(\mathbb{R}^2\):
\(\dot{x} = \mu x^2\),
\[\dot{y} = y, (x, y) \in \mathbb{R}^2, \label{8.1}\]
donde\(\mu\) es un parámetro (real). Los puntos de equilibrio de (8.1) están dados por:
\[(x, y) = (\sqrt{μ}, 0), (-\sqrt{μ}, 0). \label{8.2}\]
Es fácil ver que no hay puntos de equilibrio para\(\mu < 0\), un punto de equilibrio para\(\mu = 0\), y dos puntos de equilibrio para\(\mu > 0\).
El jacobiano del campo vectorial evaluado en cada punto de equilibrio viene dado por:
\[(\sqrt{μ}, 0): \begin{pmatrix} {-2\sqrt{μ}}&{0}\\ {0}&{-1} \end{pmatrix}, \label{8.3}\]
de lo que se deduce que los equilibrios son hiperbólicos y asintóticamente estables para\(\mu > 0\), y no hiperbólicos para\(\mu = 0\).
\[(-\sqrt{μ}, 0): \begin{pmatrix} {2\sqrt{μ}}&{0}\\ {0}&{1} \end{pmatrix} \label{8.4}\]
de lo que se deduce que los equilibrios son puntos de silla hiperbólicos para\(\mu > 0\), y no hiperbólicos para\(\mu = 0\). Destacamos nuevamente que no hay puntos de equilibrio para\(\mu < 0\).
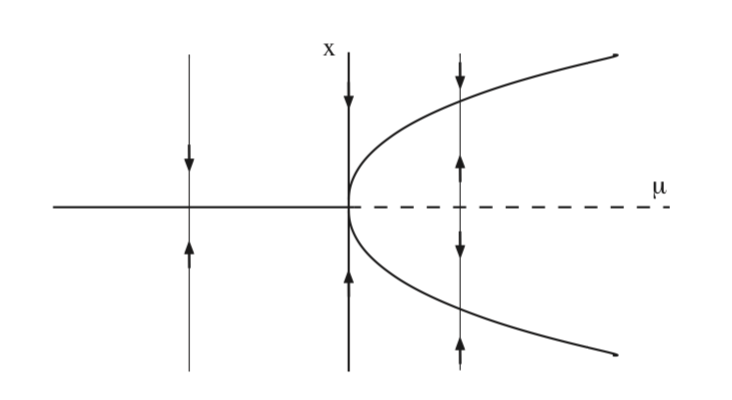
Como resultado de la “estructura” de (8.1) podemos representar fácilmente el comportamiento de los equilibrios en función de\(\mu\) en un diagrama de bifurcación. Es decir, dado que los componentes x e y de (8.1) están “desacoplados”, y el cambio en el número y la estabilidad de los equilibrios nos capturan completamente por las coordenadas x, podemos trazar la componente x del campo vectorial en función de\(\mu\), como mostramos en la Fig. 8.1.
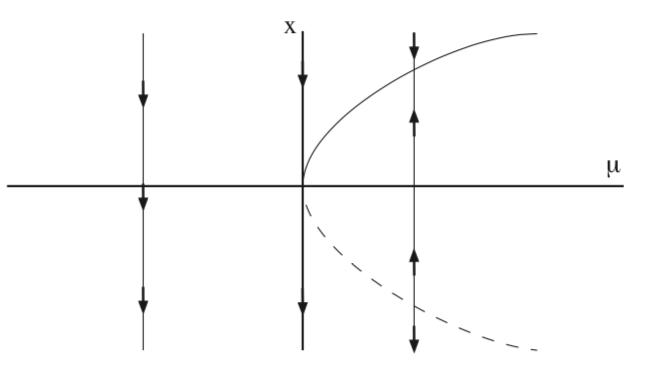
En la Fig. 8.2 se ilustra la bifurcación de equilibrios para (8.1) en el\(x - y\) plano.
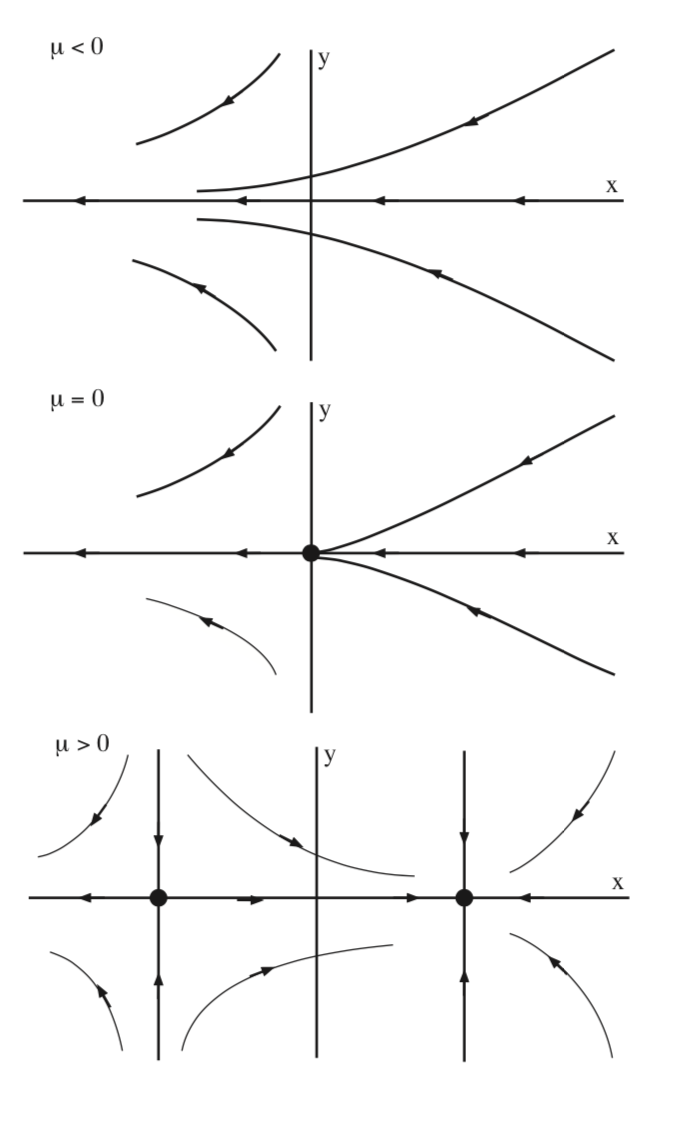
Este tipo de bifurcación se conoce como bifurcación de nodo de silla de montar (ocasionalmente también se puede denominar bifurcación plegada o bifurcación tangente, pero estos términos se usan con menos frecuencia).
La característica clave de la bifurcación del nodo de silla de montar es la siguiente. A medida que se varía un parámetro (\(\mu\)), el número de equilibrios cambia de cero a dos, y el cambio ocurre a un valor de parámetro correspondiente a los dos equilibrios que se coalescen en un equilibrio no hiperbólico.
\(\mu\)se llama el parámetro de bifurcación y\(\mu = 0\) se denomina punto de bifurcación.
Ejemplo\(\PageIndex{23}\) (The Transcritical Bifurcation)
Considere el siguiente campo vectorial autónomo no lineal en\(\mathbb{R}^2\):
\(\dot{x} = \mu x-x^2\),
\[\dot{y} = y, (x, y) \in \mathbb{R}^2, \label{8.5}\]
donde\(\mu\) es un parámetro (real). Los puntos de equilibrio de (8.5) están dados por:
\[(x, y) = (0, 0), (\mu, 0). \label{8.6}\]
El jacobiano del campo vectorial evaluado en cada punto de equilibrio viene dado por:
\[(0,0) \begin{pmatrix} {\mu}&{0}\\ {0}&{-1} \end{pmatrix} \label{8.7}\]
\[(\mu, 0) \begin{pmatrix} {-\mu}&{0}\\ {0}&{1} \end{pmatrix} \label{8.8}\]
de donde se deduce que (0, 0) es asintóticamente estable para\(\mu < 0\), y una silla hiperbólica para\(\mu > 0\), y\((\mu, 0)\) es una silla hiperbólica para\(\mu < 0\) y asintóticamente estable para\(\mu > 0\). Estas dos líneas de puntos fijos se cruzan en\(\mu = 0\), en la que sólo hay uno, punto fijo no hiperbólico.
En la Fig. 8.3 mostramos el diagrama de bifurcación para (8.5) en el\(\mu - x\) plano.
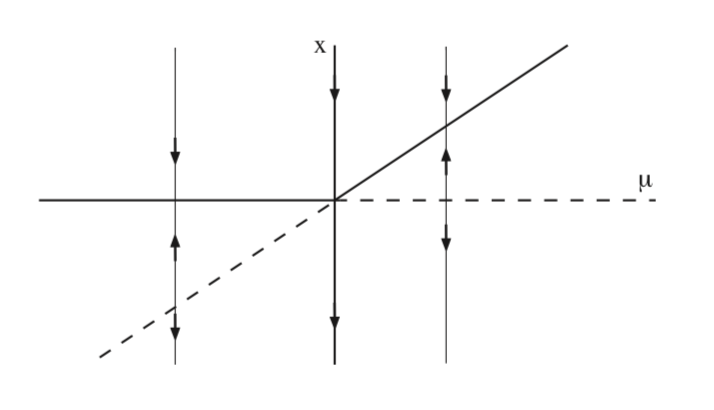
En la Fig. 8.4 ilustramos la bifurcación de equilibrios para (8.5) en el\(x - y\) plano para\(\mu < 0\),\(\mu = 0\), y\(\mu > 0\).
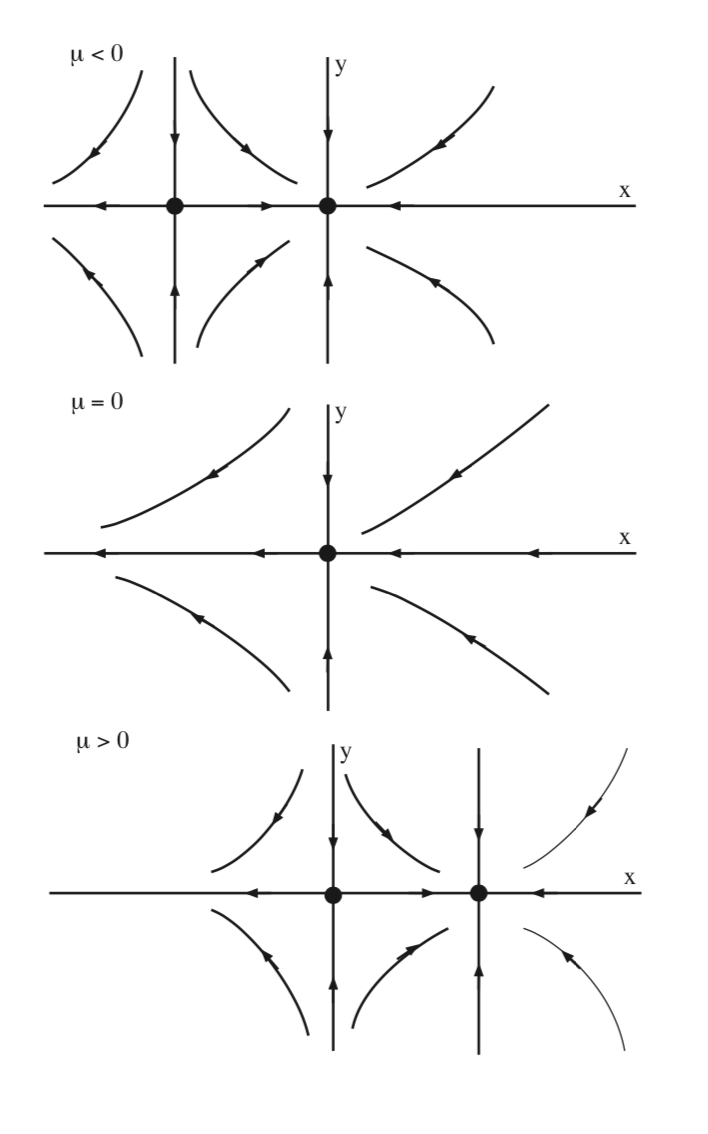
Este tipo de bifurcación se conoce como bifurcación transcrítica.
La característica clave de la bifurcación transcrítica es la siguiente. A medida que se varía un parámetro (\(\mu\)), el número de equilibrios cambia de dos a uno, y de nuevo a dos, y el cambio en el número de equilibrios ocurre a un valor de parámetro correspondiente a los dos equilibrios que se funden en un equilibrio no hiperbólico.
Ejemplo\(\PageIndex{24}\) (The (Supercritical) Pitchfork Bifurcation).
Considere el siguiente campo vectorial autónomo no lineal en\(\mathbb{R}^2\):
\(\dot{x} = \mu x-x^3\),
\[\dot{y} = -y, (x, y) \in \mathbb{R}^2, \label{8.9}\]
donde\(\mu\) es un parámetro (real). Los puntos de equilibrio de (8.9) están dados por:
\[(x, y) = (0, 0), (\sqrt{\mu}, 0), (-\sqrt{\mu}, 0) \label{8.10}\]
El jacobiano del campo vectorial evaluado en cada punto de equilibrio viene dado por:
\[(0, 0) \begin{pmatrix} {\mu}&{0}\\ {0}&{1} \end{pmatrix} \label{8.11}\]
\[(\pm \sqrt{μ}, 0) \begin{pmatrix} {-2\mu}&{0}\\ {0}&{1} \end{pmatrix} \label{8.12}\]
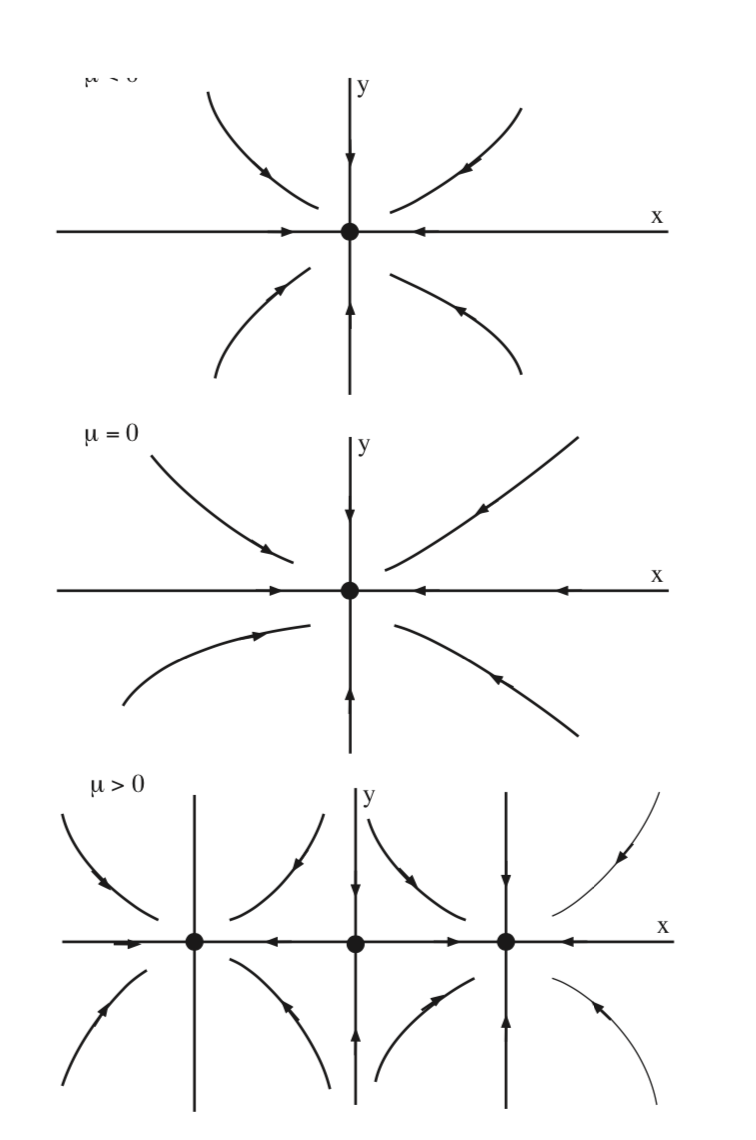
de donde se deduce que (0, 0) es asintóticamente estable para\(\mu < 0\), y una silla hiperbólica para\(\mu > 0\), y\(( \pm \sqrt{μ}, 0)\) son asintóticamente estables para\(\mu > 0\), y no existen para\(\mu < 0\). Estas dos curvas de puntos fijos pasan por cero at\(\mu = 0\), en la que solo hay uno, punto fijo no hiperbólico.
En la Fig. 8.5 mostramos el diagrama de bifurcación para (8.9) en el\(\mu - x\) plano.
En la Fig. 8.6 se ilustra la bifurcación de equilibrios para (8.9) en el\(x - y\) plano para\(\mu < 0\),\(\mu = 0\), y\(\mu > 0\).
Ejemplo\(\PageIndex{25}\) (The (Subcritical) Pitchfork Bifurcation)
Considere el siguiente campo vectorial autónomo no lineal en\(\mathbb{R}^2\):
\(\dot{x} = \mu x+x^3\),
\[\dot{y} = y, (x, y) \in \mathbb{R}^2, \label{8.13}\]
donde\(\mu\) es un parámetro (real). Los puntos de equilibrio de (8.9) están dados por:
\[(x, y) = (0, 0), (\sqrt{μ}, 0), (-\sqrt{μ}, 0). \label{8.14}\]
El jacobiano del campo vectorial evaluado en cada punto de equilibrio viene dado por:
\[(0, 0) \begin{pmatrix} {\mu}&{0}\\ {0}&{-1} \end{pmatrix} \label{8.15}\]
\[(\pm \sqrt{\mu}, 0) \begin{pmatrix} {-2\mu}&{0}\\ {0}&{1} \end{pmatrix} \label{8.16}\]
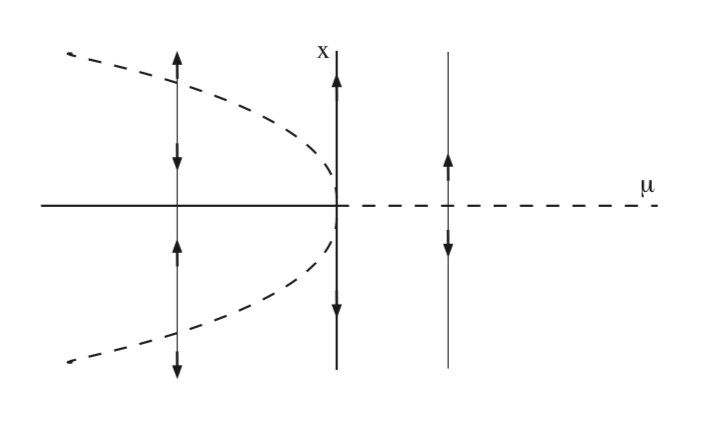
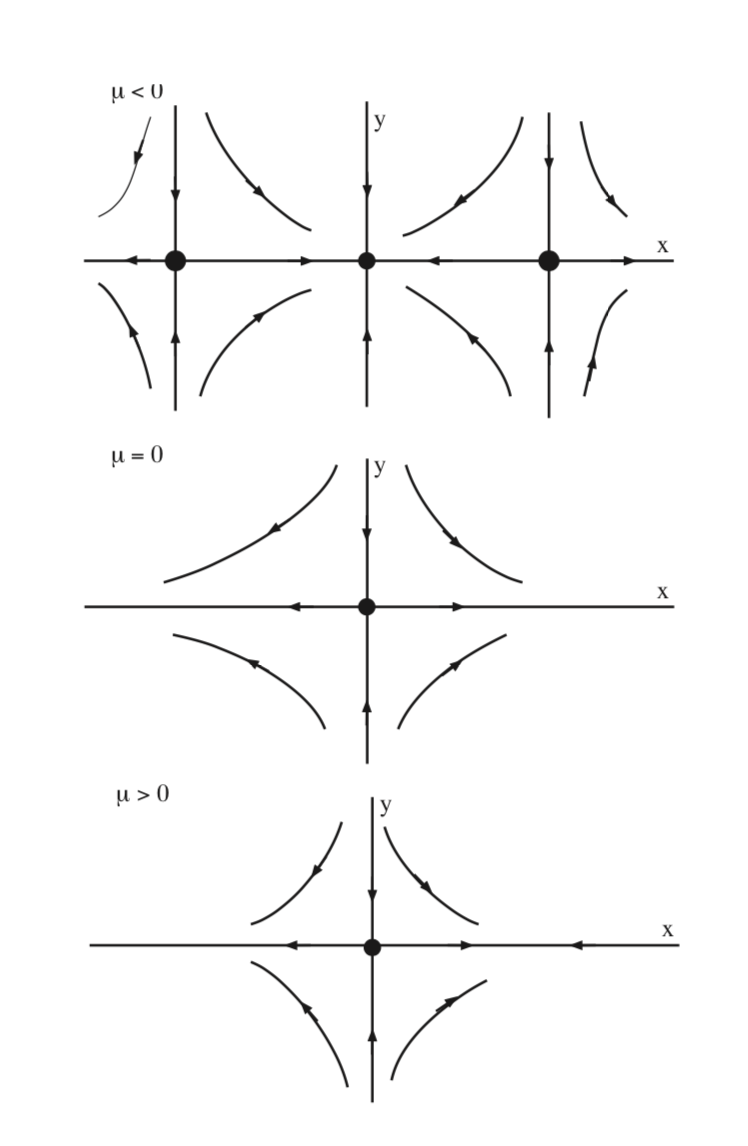
de donde se deduce que (0, 0) es asintóticamente estable para\(\mu < 0\), y un sillín hiperbólico para\(\mu > 0\), y\((\pm \sqrt{μ}, 0)\) son sillines hiperbólicos para\(\mu < 0\), y no existen para\(\mu > 0\). Estas dos curvas de puntos fijos pasan por cero at\(\mu = 0\), en la que solo hay uno, punto fijo no hiperbólico. En la Fig. 8.7 se muestra el diagrama de bifurcación para (8.13) en el\(\mu - x\) plano.
En la Fig. 8.8 se ilustra la bifurcación de equilibrios para (8.9) en el\(x - y\) plano para\(\mu < 0\),\(\mu = 0\), y\(\mu > 0\).
Observamos que la frase bifurcación de horca supercrítica también se conoce como una pérdida suave de estabilidad y la frase bifurcación de horca subcrítica se conoce como una dura pérdida de estabilidad. Lo que esto significa es lo siguiente. En la bifurcación de tricidad supercrítica como\(\mu\) va de negativo a positivo el punto de equilibrio pierde estabilidad, pero a medida que\(\mu\) aumenta más allá de cero las trayectorias cercanas al origen están delimitadas en qué tan lejos del origen pueden moverse. En la bifurcación subcrítica, el origen pierde estabilidad a medida que\(\mu\) aumenta de negativo a positivo, pero las trayectorias cercanas al equilibrio inestable pueden quedar sin límites.
Es natural hacer la pregunta,
“¿Qué es lo común de estos tres ejemplos de bifurcaciones de puntos fijos de campos vectoriales autónomos unidimensionales?” Tomamos nota de lo siguiente.
- Una necesaria (pero no suficiente) para la bifurcación de un punto fijo es la no hiperbolicidad del punto fijo.
- La “naturaleza” de la bifurcación (ej. números y estabilidad de los puntos fijos que se crean o destruyen) viene determinada por la forma de la no linealidad.
Pero podríamos ir más allá y preguntarnos ¿qué tiene en común estos ejemplos que podrían llevar a una definición de la bifurcación de un punto fijo para campos vectoriales autónomos? A partir de las características comunes damos la siguiente definición.
Definición 21 (Bifurcación de un punto fijo de un campo vectorial autónomo unidimensional)
Consideramos un campo vectorial autónomo unidimensional dependiendo de un parámetro,\(\mu\). Suponemos que a cierto valor de parámetro tiene un punto fijo que no es hiperbólico. Decimos que una bifurcación ocurre a ese “valor de parámetro no hiperbólico” si para\(\mu\) en una vecindad de ese valor de parámetro cambia el número de puntos fijos y su estabilidad.
Finalmente, terminamos la discusión de bifurcaciones de un punto fijo de campos vectoriales autónomos unidimensionales con un ejemplo que muestra que un punto fijo no hiperbólico puede no bifurcarse a medida que se varía un parámetro, es decir, la no hiperbolicidad es una condición necesaria, pero no suficiente, para la bifurcación.
Ejemplo\(\PageIndex{26}\)
Consideramos el campo vectorial autónomo unidimensional:
\[\dot{x} =\mu-x^3, x \in \mathbb{R}, \label{8.17}\]
donde\(\mu\) es un parámetro. Este campo vectorial tiene un punto fijo no hiperbólico en x = 0 para\(\mu = 0\). La curva de puntos fijos en el\(\mu - x\) plano viene dada por\(\mu = x^3\), y la jacobiana del campo vectorial es\(-3x^2\), que es estrictamente negativa en todos los puntos fijos, excepto el punto fijo no hiperbólico en el origen.
En la fig. 8.9 trazamos los puntos fijos en función de\(\mu\).
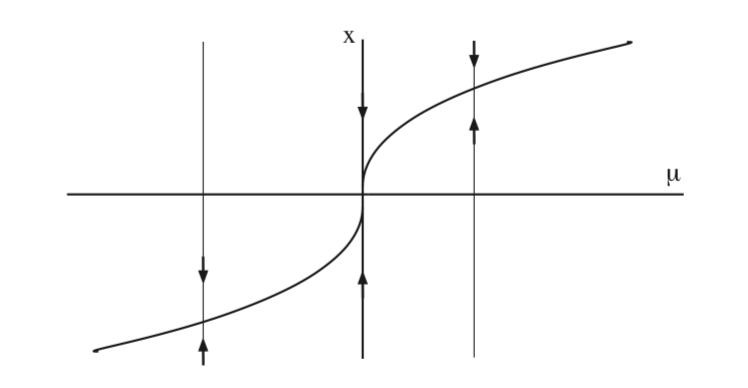
Vemos que no hay cambio en el número o estabilidad de los puntos fijos para\(\mu > 0\) y\(\mu < 0\). De ahí que no haya bifurcación.


