0.2: Introducción a las Ecuaciones Diferenciales

Ecuaciones diferenciales

Las leyes de la física generalmente se escriben como ecuaciones diferenciales. Por lo tanto, toda la ciencia y la ingeniería utilizan ecuaciones diferenciales hasta cierto punto. Comprender las ecuaciones diferenciales es esencial para entender casi cualquier cosa que estudies en tus clases de ciencias e ingeniería. Se puede pensar en las matemáticas como el lenguaje de la ciencia, y las ecuaciones diferenciales son una de las partes más importantes de este lenguaje en lo que respecta a la ciencia y la ingeniería. Como analogía, supongamos que todas sus clases a partir de ahora se dieron en swahili. Sería importante aprender primero swahili, o te lo pasaría muy mal conseguir una buena nota en tus clases.

Ya viste muchas ecuaciones diferenciales sin quizás saberlo. E incluso resolviste ecuaciones diferenciales simples cuando tomabas cálculo. Veamos un ejemplo que quizás no hayas visto:\[\label{eq:1} \frac{dx}{dt} + x = 2 \cos t . \] Aquí\(x\) está la variable dependiente y\(t\) es la variable independiente. La ecuación\(\eqref{eq:1}\) es un ejemplo básico de una ecuación diferencial. Es un ejemplo de una ecuación diferencial de primer orden, ya que involucra únicamente la primera derivada de la variable dependiente. Esta ecuación surge de la ley de enfriamiento de Newton donde la temperatura ambiente oscila con el tiempo.

Soluciones de Ecuaciones Diferenciales

Resolver la ecuación diferencial significa encontrar\(x\) en términos de\(t\). Es decir, queremos encontrar una función de\(t\), a la que llamamos\(x\), de tal manera que cuando nos conectamos\(x\)\(t\), y\(\frac{dx}{dt}\) en\(\eqref{eq:1}\), la ecuación se sostiene; es decir, el lado izquierdo es igual al lado derecho. Es la misma idea que sería para una ecuación normal (algebraica) de justo\(x\) y\(t\). Afirmamos que\[x = x(t) = \cos t + \sin t \nonumber \] es una solución. ¿Cómo verificamos? ¡Simplemente nos conectamos\(x\) a la ecuación\(\eqref{eq:1}\)! Primero tenemos que computar\(\frac{dx}{dt}\). Nos encontramos con eso\(\frac{dx}{dt} = -\sin t + \cos t\). Ahora vamos a calcular el lado izquierdo de\(\eqref{eq:1}\). \[\frac{dx}{dt} + x = \underbrace{(-\sin t + \cos t)}_{\frac{dx}{dt}} + \underbrace{(\cos t + \sin t)}_{x} = 2\cos t . \nonumber \]¡Yay! Obtuvimos precisamente el lado derecho. ¡Pero hay más! Afirmamos también\(x = \cos t + \sin t + e^{-t}\) es una solución. Vamos a intentarlo,\[\frac{dx}{dt} = -\sin t + \cos t - e^{-t} . \nonumber \] Nos conectamos al lado izquierdo de ¡\(\eqref{eq:1}\)\[\frac{dx}{dt} + x = \underbrace{(-\sin t + \cos t - e^{-t})}_{\frac{dx}{dt}} + \underbrace{(\cos t + \sin t + e^{-t})}_{x} = 2\cos t . \nonumber \]Y funciona una vez más!

Entonces puede haber muchas soluciones diferentes. Para esta ecuación todas las soluciones se pueden escribir en la forma\[x = \cos t + \sin t + C e^{-t} , \nonumber \] para alguna constante\(C\). Diferentes constantes\(C\) darán diferentes soluciones, por lo que realmente hay infinitamente muchas soluciones posibles. Consulte la Figura\(\PageIndex{1}\) para ver la gráfica de algunas de estas soluciones. Veremos cómo encontramos estas soluciones unas cuantas conferencias a partir de ahora.

Figura\(\PageIndex{1}\): Pocas soluciones de\(\frac{dx}{dt}+x=2\cos t\).

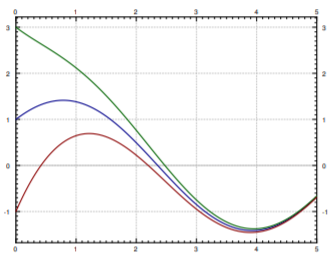
Resolver ecuaciones diferenciales puede ser bastante difícil. No existe un método general que resuelva cada ecuación diferencial. Generalmente nos centraremos en cómo obtener fórmulas exactas para soluciones de ciertas ecuaciones diferenciales, pero también dedicaremos un poco de tiempo a obtener soluciones aproximadas. Y dedicaremos algún tiempo a entender las ecuaciones sin resolverlas.

La mayor parte de este libro está dedicado a ecuaciones diferenciales ordinarias u ODEs, es decir, ecuaciones con una sola variable independiente, donde las derivadas son sólo con respecto a esta variable. Si hay varias variables independientes, obtenemos ecuaciones diferenciales parciales o PDEs.

Incluso para las ODE, que son muy bien entendidas, no se trata de una simple cuestión de girar una manivela para obtener respuestas. Cuando puedes encontrar soluciones exactas, suelen ser preferibles a las soluciones aproximadas. Es importante entender cómo se encuentran tales soluciones. Aunque en aplicaciones reales dejarás gran parte de los cálculos reales a las computadoras, necesitas entender lo que están haciendo. Muchas veces es necesario simplificar o transformar tus ecuaciones en algo que una computadora pueda entender y resolver. Es posible que incluso necesites hacer ciertas suposiciones y cambios en tu modelo para lograrlo.

Para ser un ingeniero o científico exitoso, se te requerirá que resuelvas problemas en tu trabajo que nunca antes habías visto. Es importante aprender técnicas de resolución de problemas, para que puedas aplicar esas técnicas a nuevos problemas. Un error común es esperar aprender alguna prescripción para resolver todos los problemas que encontrarás en tu carrera posterior. Este curso no es la excepción.

Ecuaciones diferenciales en la práctica

Figura\(\PageIndex{2}\)

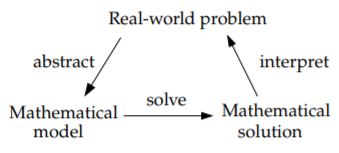
Entonces, ¿cómo utilizamos las ecuaciones diferenciales en ciencia e ingeniería? Primero, tenemos algún problema del mundo real que deseamos entender. Hacemos algunas suposiciones simplificadoras y creamos un modelo matemático. Es decir, traducimos la situación del mundo real en un conjunto de ecuaciones diferenciales. Luego aplicamos las matemáticas para obtener algún tipo de solución matemática. Todavía queda algo por hacer. Tenemos que interpretar los resultados. Tenemos que averiguar qué dice la solución matemática sobre el problema del mundo real con el que empezamos.

Aprender a formular el modelo matemático y a interpretar los resultados es lo que hacen tus clases de física e ingeniería. En este curso, nos centraremos principalmente en el análisis matemático. A veces trabajaremos con ejemplos simples del mundo real para que tengamos cierta intuición y motivación sobre lo que estamos haciendo.

Veamos un ejemplo de este proceso. Una de las ecuaciones diferenciales más básicas es el modelo de crecimiento exponencial estándar. Dejar\(P\) denotar la población de algunas bacterias en una placa de Petri. Asumimos que hay suficiente comida y suficiente espacio. Entonces la tasa de crecimiento de las bacterias es proporcional a la población—una gran población crece más rápido. Vamos a\(t\) denotar el tiempo (digamos en segundos) y\(P\) la población. Nuestro modelo es\[\frac{dP}{dt} = kP , \nonumber \] para alguna constante positiva\(k > 0\).

Ejemplo\(\PageIndex{1}\)

Supongamos que hay\(100\) bacterias a la vez\(0\) y\(200\) bacterias\(10\) segundos después. ¿Cuántas bacterias habrá\(1\) minuto a partir de tiempo\(0\) (en\(60\) segundos)?

Figura\(\PageIndex{2}\): Crecimiento bacteriano en los primeros\(60\) segundos.

Solución

Primero tenemos que resolver la ecuación. Afirmamos que una solución viene dada por\[P(t) = C e^{kt} , \nonumber \] donde\(C\) es una constante. Intentemos:\[\frac{dP}{dt} = C k e^{kt} = k P . \nonumber \] Y realmente es una solución.

Bien, ¿y ahora qué? No sabemos\(C\), y no sabemos\(k\). Pero sabemos algo. Sabemos\(P(0) = 100\), y lo sabemos\(P(10) = 200\). Vamos a enchufar estas condiciones y ver qué pasa. \[\begin{align}\begin{aligned} & 100 = P(0) = C e^{k0} = C ,\\ & 200 = P(10) = 100 \, e^{k10} .\end{aligned}\end{align} \nonumber \]Por lo tanto,\(2 = e^{10k}\) o\(\frac{\ln 2}{10} = k \approx 0.069\). Entonces\[P(t) = 100 \, e^{(\ln 2) t / 10} \approx 100 \, e^{0.069 t} . \nonumber \] a un minuto,\(t=60\), la población es\(P(60) = 6400\). Ver Figura\(\PageIndex{2}\).

Hablemos de la interpretación de los resultados. ¿Nuestra solución significa que debe haber exactamente\(6400\) bacterias en el plato en\(60\text{s}\)? ¡No! Hicimos suposiciones que podrían no ser ciertas exactamente, solo aproximadamente. Si nuestras suposiciones son razonables, entonces habrá aproximadamente\(6400\) bacterias. También, en la vida real\(P\) es una cantidad discreta, no un número real. No obstante, nuestro modelo no tiene ningún problema en decir que por ejemplo a los\(61\) segundos,\(P(61) \approx 6859.35\).

Normalmente,\(P' = kP\) se conoce el\(k\) in, y queremos resolver la ecuación para diferentes condiciones iniciales. ¿Qué significa eso? Toma\(k=1\) por simplicidad. Supongamos que queremos resolver la ecuación\(\frac{dP}{dt} = P\) sujeta a\(P(0) = 1000\) (la condición inicial). Entonces la solución resulta ser (ejercicio)\[P(t) = 1000 \, e^t . \nonumber \]

Llamamos a\(P(t) = C e^t\) la solución general, ya que cada solución de la ecuación puede escribirse en esta forma para alguna constante\(C\). Necesitamos una condición inicial para saber qué\(C\) es, a fin de encontrar la solución particular que estamos buscando. Generalmente, cuando decimos “solución particular”, solo nos referimos a alguna solución.

Ecuaciones Fundamentales

Algunas ecuaciones aparecen a menudo y es útil simplemente memorizar cuáles son sus soluciones. Llamémoslas las cuatro ecuaciones fundamentales. Sus soluciones son razonablemente fáciles de adivinar al recordar las propiedades de exponenciales, senos y cosenos. También son simples de verificar, que es algo que siempre debes hacer. No hace falta preguntarse si recordaste la solución correctamente.

En primer lugar tal ecuación es\[\frac{dy}{dx} = k y , \nonumber \] para alguna constante\(k > 0\). Aquí\(y\) está la variable dependiente y\(x\) la independiente. La solución general para esta ecuación es\[y(x) = C e^{kx} . \nonumber \] Vimos anteriormente que esta función es una solución, aunque utilizamos diferentes nombres de variables.

A continuación,\[\frac{dy}{dx} = -k y , \nonumber \] para alguna constante\(k > 0\). La solución general para esta ecuación es\[y(x) = C e^{-kx} . \nonumber \]

Ejercicio\(\PageIndex{1}\)

Comprobar que lo\(y\) dado es realmente una solución a la ecuación.

A continuación, tomar la ecuación diferencial de segundo orden\[\frac{d^2y}{{dx}^2} = -k^2 y , \nonumber \] para alguna constante\(k > 0\). La solución general para esta ecuación es\[y(x) = C_1 \cos(kx) + C_2 \sin(kx) . \nonumber \] Dado que la ecuación es una ecuación diferencial de segundo orden, tenemos dos constantes en nuestra solución general.

Ejercicio\(\PageIndex{2}\)

Comprobar que lo\(y\) dado es realmente una solución a la ecuación.

Finalmente, considere la ecuación diferencial de segundo orden\[\frac{d^2y}{{dx}^2} = k^2 y , \nonumber \] para alguna constante\(k > 0\). La solución general para esta ecuación es\[y(x) = C_1 e^{kx} + C_2 e^{-kx} , \nonumber \] o\[y(x) = D_1 \cosh(kx) + D_2 \sinh(kx) . \nonumber \]

Para aquellos que no saben,\(\cosh\) y\(\sinh\) se definen por\[\cosh x = \frac{e^{x} + e^{-x}}{2} , \qquad \sinh x = \frac{e^{x} - e^{-x}}{2} . \nonumber \] Se llaman coseno hiperbólico y seno hiperbólico. Estas funciones son a veces más fáciles de trabajar que las exponenciales. Tienen algunas propiedades familiares agradables como\(\cosh 0 = 1\),\(\sinh 0 = 0\), y\(\frac{d}{dx} \cosh x = \sinh x\) (no, eso no es un error tipográfico) y\(\frac{d}{dx} \sinh x = \cosh x\).

Ejercicio\(\PageIndex{3}\)

Comprobar que ambas formas de lo\(y\) dado son realmente soluciones a la ecuación.

Ejemplo\(\PageIndex{2}\)

En ecuaciones de orden superior, obtienes más constantes que debes resolver para obtener una solución particular. La ecuación\(\frac{d^2y}{dx^2} = 0\) tiene la solución general\(y = C_1 x + C_2\); simplemente integre dos veces y no se olvide de la constante de integración. Considerar las condiciones iniciales\(y(0) = 2\) y\(y'(0) = 3\). Enchufamos nuestra solución general y resolvemos para las constantes:\[2 = y(0) = C_1 \cdot 0 + C_2 = C_2, \qquad 3 = y'(0) = C_1 . \nonumber \] En otras palabras,\(y = 3x + 2\) es la solución particular que buscamos.

Una nota interesante sobre\(\cosh\): La gráfica de\(\cosh\) es la forma exacta de una cadena colgante. Esta forma se llama catenaria. Contrario a la creencia popular esto no es una parábola. Si inviertes la gráfica de\(\cosh\), también es el arco ideal para soportar su peso. Por ejemplo, el arco de la puerta de entrada en Saint Louis es una gráfica invertida de\(\cosh\) —si fuera solo una parábola podría caer. La fórmula utilizada en el diseño está inscrita dentro del arco:\[y = -127.7 \; \textrm{ft} \cdot \cosh({x / 127.7 \; \textrm{ft}}) + 757.7 \; \textrm{ft} . \nonumber \]