A.6: Determinante

Para matrices cuadradas definimos una cantidad útil llamada determinante. Definir el determinante de una\(1 \times 1\) matriz como el valor de su única entrada\[\det \left( \begin{bmatrix} a \end{bmatrix} \right) \overset{\text{def}}{=} a . \nonumber \] Para una\(2 \times 2\) matriz, defina\[\det \left( \begin{bmatrix} a & b \\ c & d \end{bmatrix} \right) \overset{\text{def}}{=} ad-bc . \nonumber \] Antes de definir el determinante para matrices más grandes, observamos el significado del determinante. Una\(n \times n\) matriz da un mapeo del espacio euclidiano\(n\) -dimensional\({\mathbb{R}}^n\) a sí misma. Entonces una\(2 \times 2\) matriz\(A\) es un mapeo del plano a sí mismo. El determinante de\(A\) es el factor por el cual cambia el área de los objetos. Si tomamos el cuadrado unitario (cuadrado del lado 1) en el plano, entonces\(A\) toma el cuadrado a un paralelogramo de área\(\lvert\det(A)\rvert\). El signo de\(\det(A)\) denota un cambio de orientación (negativo si los ejes se voltean). Por ejemplo, vamos\[A = \begin{bmatrix} 1 & 1 \\ -1 & 1 \end{bmatrix} . \nonumber \] Entonces\(\det(A) = 1+1 = 2\). Veamos a dónde\(A\) envía la unidad cuadrada: el cuadrado con vértices\((0,0)\),\((1,0)\),\((0,1)\), y\((1,1)\). El punto\((0,0)\) es enviado a\((0,0)\). \[\begin{bmatrix} 1 & 1 \\ -1 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 1 \\ -1 \end{bmatrix} , \qquad \begin{bmatrix} 1 & 1 \\ -1 & 1 \end{bmatrix} \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \end{bmatrix} , \qquad \begin{bmatrix} 1 & 1 \\ -1 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 2 \\ 0 \end{bmatrix} . \nonumber \]La imagen del cuadrado es otro cuadrado con vértices\((0,0)\),\((1,-1)\),\((1,1)\), y\((2,0)\). El cuadrado de la imagen tiene un lado de largo\(\sqrt{2}\), y por lo tanto es de área\(2\). Ver Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Imagen de la unidad cuadrada a través del mapeo\(A\).

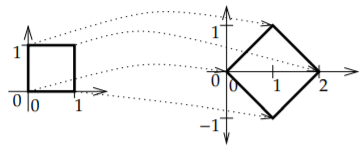
En general, la imagen de un cuadrado va a ser un paralelogramo. En geometría de secundaria, es posible que hayas visto una fórmula para computar el área de una con vértices\((0,0)\),\((a,c)\),\((b,d)\) y\((a+b,c+d)\). El área es\[\left\lvert \, \det \left( \begin{bmatrix} a & b \\ c & d \end{bmatrix} \right) \, \right\lvert = \lvert a d - b c \rvert . \nonumber \] Las líneas verticales por encima del valor absoluto medio. La matriz\(\left[ \begin{smallmatrix} a & b \\ c & d \end{smallmatrix} \right]\) lleva el cuadrado unitario al paralelogramo dado.

Hay varias formas de definir el determinante para una\(n \times n\) matriz. Usemos la llamada expansión de cofactores. Definimos\(A_{ij}\) como la matriz\(A\) con la\(i^{\text{th}}\) fila y la\(j^{\text{th}}\) columna borradas. Por ejemplo, si Ahora\[\text{If} \qquad A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} , \qquad \text{then} \qquad A_{12} = \begin{bmatrix} 4 & 6 \\ 7 & 9 \end{bmatrix} \qquad \text{and} \qquad A_{23} = \begin{bmatrix} 1 & 2 \\ 7 & 8 \end{bmatrix} . \nonumber \] definimos el determinante recursivamente\[\det (A) \overset{\text{def}}{=} \sum_{j=1}^n {(-1)}^{1+j} a_{1j} \det (A_{1j}) , \nonumber \] o en otras palabras\[\det (A) = a_{11} \det (A_{11}) - a_{12} \det (A_{12}) + a_{13} \det (A_{13}) - \cdots \begin{cases} + a_{1n} \det (A_{1n}) & \text{if } n \text{ is odd,} \\ - a_{1n} \det (A_{1n}) & \text{if } n \text{ even.} \end{cases} \nonumber \] Para una\(3 \times 3\) matriz, obtenemos\(\det (A) = a_{11} \det (A_{11}) - a_{12} \det (A_{12}) + a_{13} \det (A_{13})\). Por ejemplo,\[\begin{align}\begin{aligned} \det \left( \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} \right) & = 1 \cdot \det \left( \begin{bmatrix} 5 & 6 \\ 8 & 9 \end{bmatrix} \right) - 2 \cdot \det \left( \begin{bmatrix} 4 & 6 \\ 7 & 9 \end{bmatrix} \right) + 3 \cdot \det \left( \begin{bmatrix} 4 & 5 \\ 7 & 8 \end{bmatrix} \right) \\ & = 1 (5 \cdot 9 - 6 \cdot 8) - 2 (4 \cdot 9 - 6 \cdot 7) + 3 (4 \cdot 8 - 5 \cdot 7) = 0 . \end{aligned}\end{align} \nonumber \] resulta que no tuvimos que usar necesariamente la primera fila. Eso es para cualquier\(i\), a veces\[\det (A) = \sum_{j=1}^n {(-1)}^{i+j} a_{ij} \det (A_{ij}) . \nonumber \] es útil usar una fila distinta a la primera. En el siguiente ejemplo es más conveniente expandirse a lo largo de la segunda fila. Observe que para la segunda fila estamos comenzando con un signo negativo. \[\begin{align}\begin{aligned} \det \left( \begin{bmatrix} 1 & 2 & 3 \\ 0 & 5 & 0 \\ 7 & 8 & 9 \end{bmatrix} \right) & = - 0 \cdot \det \left( \begin{bmatrix} 2 & 3 \\ 8 & 9 \end{bmatrix} \right) + 5 \cdot \det \left( \begin{bmatrix} 1 & 3 \\ 7 & 9 \end{bmatrix} \right) - 0 \cdot \det \left( \begin{bmatrix} 1 & 2 \\ 7 & 8 \end{bmatrix} \right) \\ & = 0 + 5 (1 \cdot 9 - 3 \cdot 7) + 0 = -60 . \end{aligned}\end{align} \nonumber \]Comprobemos si realmente es lo mismo que expandirnos a lo largo de la primera fila,\[\begin{align}\begin{aligned} \det \left( \begin{bmatrix} 1 & 2 & 3 \\ 0 & 5 & 0 \\ 7 & 8 & 9 \end{bmatrix} \right) & = 1 \cdot \det \left( \begin{bmatrix} 5 & 0 \\ 8 & 9 \end{bmatrix} \right) - 2 \cdot \det \left( \begin{bmatrix} 0 & 0 \\ 7 & 9 \end{bmatrix} \right) + 3 \cdot \det \left( \begin{bmatrix} 0 & 5 \\ 7 & 8 \end{bmatrix} \right) \\ & = 1 (5 \cdot 9 - 0 \cdot 8) - 2 (0 \cdot 9 - 0 \cdot 7) + 3 (0 \cdot 8 - 5 \cdot 7) = -60 . \end{aligned}\end{align} \nonumber \] Al calcular el determinante, alternativamente sumamos y restamos los determinantes de las submatrices\(A_{ij}\) multiplicados por\(a_{ij}\) para un fijo\(i\) y todo\(j\). Los números\({(-1)}^{i+j}\det(A_{ij})\) se denominan cofactores de la matriz. Y es por ello que este método de computar el determinante se llama la expansión del cofactor.

De igual manera no necesitamos expandirnos a lo largo de una fila, podemos expandirnos a lo largo de una columna. Para cualquiera\(j\),\[\det (A) = \sum_{i=1}^n {(-1)}^{i+j} a_{ij} \det (A_{ij}) . \nonumber \] Un hecho relacionado es que\[\det (A) = \det (A^T) . \nonumber \] A matriz es triangular superior si todos los elementos por debajo de la diagonal principal son\(0\). Por ejemplo,\[\begin{bmatrix} 1 & 2 & 3 \\ 0 & 5 & 6 \\ 0 & 0 & 9 \end{bmatrix} \nonumber \] es triangular superior. De igual manera una matriz triangular inferior es aquella en la que todo por encima de la diagonal es cero. Por ejemplo,\[\begin{bmatrix} 1 & 0 & 0 \\ 4 & 5 & 0 \\ 7 & 8 & 9 \end{bmatrix} . \nonumber \] El determinante para matrices triangulares es muy sencillo de calcular. Considera la matriz triangular inferior. Si nos expandimos a lo largo de la primera fila, encontramos que el determinante es 1 veces el determinante de la matriz triangular inferior\(\left[ \begin{smallmatrix} 5 & 0 \\ 8 & 9 \end{smallmatrix} \right]\). Entonces el deteriminante es solo el producto de las entradas diagonales:\[\det \left( \begin{bmatrix} 1 & 0 & 0 \\ 4 & 5 & 0 \\ 7 & 8 & 9 \end{bmatrix} \right) = 1 \cdot 5 \cdot 9 = 45 . \nonumber \] De manera similar para matrices triangulares superiores\[\det \left( \begin{bmatrix} 1 & 2 & 3 \\ 0 & 5 & 6 \\ 0 & 0 & 9 \end{bmatrix} \right) = 1 \cdot 5 \cdot 9 = 45 . \nonumber \] En general, si\(A\) es triangular, entonces\[\det (A) = a_{11} a_{22} \cdots a_{nn} . \nonumber \] Si\(A\) es diagonal, entonces también es triangular (superior e inferior), por lo que aplica la misma fórmula. Por ejemplo,\[\det \left( \begin{bmatrix} 2 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 5 \end{bmatrix} \right) = 2 \cdot 3 \cdot 5 = 30 . \nonumber \] en particular, la matriz de identidad\(I\) es diagonal, y las entradas diagonales son todas 1. Así,\[\det(I) = 1 . \nonumber \] El determinante te está diciendo cómo escalan los objetos geométricos. Si\(B\) duplica los tamaños de los objetos geométricos y los\(A\) triplica, entonces\(AB\) (que se aplica\(B\) a un objeto y luego aplica\(A\)) debería hacer que el tamaño suba por un factor de\(6\). Esto es cierto en general:

Teorema\(\PageIndex{1}\)

\[\det(AB) = \det(A)\det(B) . \nonumber \]

Esta propiedad es una de las más útiles, y se emplea a menudo para realmente calcular determinantes. Una consecuencia particularmente interesante es señalar lo que significa para la existencia de inversos. Tomar\(A\) y\(B\) ser inversos, es decir\(AB=I\). Entonces\[\det(A)\det(B) = \det(AB) = \det(I) = 1 . \nonumber \] ni\(\det(A)\) tampoco\(\det(B)\) puede ser cero. Este hecho es una propiedad extremadamente útil del determinante, y que se utiliza a menudo en este libro:

Teorema\(\PageIndex{2}\)

Una\(n \times n\) matriz\(A\) es invertible si y solo si\(\det (A) \not= 0\).

De hecho,\(\det(A^{-1}) \det(A) = 1\) dice que\[\det(A^{-1}) = \frac{1}{\det(A)}. \nonumber \] Así sabemos cuál\(A^{-1}\) es el determinante de sin computación\(A^{-1}\).

Volvamos a la fórmula para la inversa de una\(2 \times 2\) matriz:\[\begin{bmatrix} a & b \\ c & d \end{bmatrix}^{-1} = \frac{1}{ad-bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix} . \nonumber \] Observe el determinante de la matriz\([\begin{smallmatrix}a&b\\c&d\end{smallmatrix}]\) en el denominador de la fracción. La fórmula sólo funciona si el determinante es distinto de cero, de lo contrario estamos dividiendo por cero.

Una notación común para el determinante es un par de líneas verticales:\[\begin{vmatrix} a & b \\ c & d \end{vmatrix} = \det \left( \begin{bmatrix} a & b \\ c & d \end{bmatrix} \right) . \nonumber \] Personalmente, encuentro esta notación confusa ya que las líneas verticales suelen significar una cantidad positiva, mientras que los determinantes pueden ser negativos. También piensa en cómo escribir el valor absoluto de un determinante. Esta notación no se utiliza en este libro.