A.5: Producto Interior y Proyecciones

Producto interno y ortogonalidad

Para hacer geometría básica, necesitamos longitud, y necesitamos ángulos. Ya hemos visto la longitud euclidiana, así que descubramos cómo calcular los ángulos. En su mayoría, nos preocupa el ángulo correcto \(^{1}\).

Dados dos vectores (columna) en\({\mathbb{R}}^n\), definimos el producto interno (estándar) como el producto punto:\[\langle \vec{x} , \vec{y} \rangle = \vec{x} \cdot \vec{y} = \vec{y}^T \vec{x} = x_1 y_1 + x_2 y_2 + \cdots + x_n y_n = \sum_{i=1}^n x_i y_i . \nonumber \] ¿Por qué aparentemente damos una nueva notación para el producto punto? Porque hay otros posibles productos internos, que no son el producto punto, aunque no nos vamos a preocupar por otros aquí. Un producto interior puede incluso definirse en espacios de funciones como lo hacemos en el Capítulo 4:\[\langle f(t) , g(t) \rangle = \int_{a}^{b} f(t) g(t) \, dt . \nonumber \] Pero nosotros digremos.

El producto interno cumple con las siguientes reglas:

1. \(\langle \vec{x} , \vec{x} \rangle \geq 0\), y\(\langle \vec{x} , \vec{x} \rangle = 0\) si y sólo si\(\vec{x} = 0\),
2. \(\langle \vec{x} , \vec{y} \rangle = \langle \vec{y} , \vec{x} \rangle\),
3. \(\langle a\vec{x} , \vec{y} \rangle = \langle \vec{x} , a\vec{y} \rangle = a \langle \vec{x} , \vec{y} \rangle\),
4. \(\langle \vec{x} + \vec{y} , \vec{z} \rangle = \langle \vec{x} , \vec{z} \rangle + \langle \vec{y} , \vec{z} \rangle\)y\(\langle \vec{x}, \vec{y} + \vec{z} \rangle = \langle \vec{x} , \vec{y} \rangle + \langle \vec{x} , \vec{z} \rangle\).

Cualquier cosa que satisfaga las propiedades anteriores puede llamarse un producto interno, aunque en esta sección nos preocupa el producto interno estándar en\({\mathbb{R}}^n\).

El producto interno estándar da la longitud euclidiana:\[\lVert{\vec{x}}\rVert = \sqrt{\langle \vec{x}, \vec{x} \rangle} = \sqrt{x_1^2 + x_2^2 + \cdots + x_n^2} . \nonumber \] ¿Cómo da ángulos?

Puede recordar del cálculo multivariable, que en dos o tres dimensiones, el producto interno estándar (el producto punto) le da el ángulo entre los vectores: Es\[\langle \vec{x}, \vec{y} \rangle = \lVert{\vec{x}}\rVert \lVert{\vec{y}}\rVert \cos \theta. \nonumber \] decir,\(\theta\) es el ángulo que\(\vec{x}\) y\(\vec{y}\) hacen cuando se basan en el mismo punto.

En\({\mathbb{R}}^n\) (cualquier dimensión), simplemente vamos a decir que a\(\theta\) partir de la fórmula es lo que es el ángulo. Esto tiene sentido ya que dos vectores cualesquiera basados en el origen se encuentran en un plano bidimensional (subespacio), y la fórmula funciona en 2 dimensiones. De hecho, incluso se podría hablar de ángulos entre funciones de esta manera, y lo hacemos en el Capítulo 4, donde hablamos de funciones ortogonales (funciones en ángulo recto entre sí).

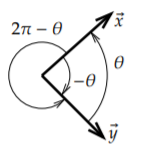
Para calcular el ángulo calculamos\[\cos \theta = \frac{\langle \vec{x}, \vec{y} \rangle}{\lVert{\vec{x}}\rVert \lVert{\vec{y}}\rVert} . \nonumber \] Nuestros ángulos están siempre en radianes. Estamos calculando el coseno del ángulo, que es realmente lo mejor que podemos hacer. Dados dos vectores en ángulo\(\theta\), podemos dar el ángulo como\(-\theta\),\(2\pi-\theta\), etc., ver Figura\(\PageIndex{1}\). Afortunadamente,\(\cos \theta = \cos (-\theta) = \cos(2\pi - \theta)\). Si resolvemos por\(\theta\) usar el coseno inverso\(\cos^{-1}\), podemos simplemente decretarlo\(0 \leq \theta \leq \pi\).

Figura\(\PageIndex{1}\): Ángulo entre vectores.

Ejemplo\(\PageIndex{1}\)

Calculemos el ángulo entre los vectores\((3,0)\) y\((1,1)\) en el plano. Calcular\[\cos \theta = \frac{\bigl\langle (3,0) , (1,1) \bigr\rangle}{\lVert(3,0)\rVert \lVert(1,1)\rVert} = \frac{3 + 0}{3 \sqrt{2}} = \frac{1}{\sqrt{2}} . \nonumber \] Por lo tanto\(\theta = \frac{\pi}{4}\).

Como decíamos, el ángulo más importante es el ángulo recto. Un ángulo recto son\(\frac{\pi}{2}\) radianes, y\(\cos (\frac{\pi}{2}) = 0\), por lo que la fórmula es particularmente fácil en este caso. Decimos vectores\(\vec{x}\) y\(\vec{y}\) son ortogonales si están en ángulo recto, es decir si\[\langle \vec{x} , \vec{y} \rangle = 0 . \nonumber \] Los vectores\((1,0,0,1)\) y\((1,2,3,-1)\) son ortogonales. Así son\((1,1)\) y\((1,-1)\). Sin embargo,\((1,1)\) y no\((1,2)\) son ortogonales como lo es su producto interno\(3\) y no\(0\).

Proyección ortogonal

Una aplicación típica del álgebra lineal es tomar un problema difícil, escribir todo en la base correcta, y en esta nueva base el problema se vuelve simple. Una base particularmente útil es una base ortogonal, es decir, una base donde todos los vectores base son ortogonales. Cuando dibujamos un sistema de coordenadas en dos o tres dimensiones, casi siempre dibujamos nuestros ejes como ortogonales entre sí.

Generalizando este concepto a funciones, resulta particularmente útil en el Capítulo 4 expresar una función utilizando una base ortogonal particular, la serie de Fourier.

Para expresar un vector en términos de una base ortogonal, primero necesitamos proyectar un vector sobre otro. Dado un vector distinto de cero\(\vec{v}\), definimos la proyección ortogonal de\(\vec{w}\) onto\(\vec{v}\) como\[\operatorname{proj}_{\vec{v}}(\vec{w}) = \left( \frac{\langle \vec{w} , \vec{v} \rangle}{ \langle \vec{v} , \vec{v} \rangle} \right) \vec{v} . \nonumber \] Para la idea geométrica, ver Figura\(\PageIndex{2}\). Es decir, encontramos la “sombra de\(\vec{w}\)" en la línea abarcada por\(\vec{v}\) si la dirección de los rayos del sol fuera exactamente perpendicular a la línea. Otra forma de pensarlo es que la punta de la flecha de\(\operatorname{proj}_{\vec{v}}(\vec{w})\) es el punto más cercano de la línea abarcado por\(\vec{v}\) hasta la punta de la flecha de\(\vec{w}\). En cuanto a distancia euclidiana,\(\vec{u} = \operatorname{proj}_{\vec{v}}(\vec{w})\) minimiza la distancia\(\lVert \vec{w} - \vec{u} \rVert\) entre todos los vectores\(\vec{u}\) que son múltiplos de\(\vec{v}\). Debido a esto, esta proyección surge a menudo en matemáticas aplicadas en todo tipo de contextos no podemos resolver un problema exactamente: No siempre podemos resolver “Encontrar\(\vec{w}\) como múltiplo de\(\vec{v}\)" pero\(\operatorname{proj}_{\vec{v}}(\vec{w})\) es la mejor “solución”.

Figura\(\PageIndex{2}\): Proyección ortogonal.

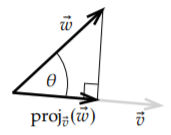
La fórmula se deriva de la trigonometría básica. La longitud de\(\operatorname{proj}_{\vec{v}}(\vec{w})\) debe ser\(\cos \theta\) veces la longitud de\(\vec{w}\), es decir\((\cos \theta)\lVert\vec{w}\rVert\). Tomamos el vector unitario en la dirección de\(\vec{v}\), es decir,\(\frac{\vec{v}}{\lVert \vec{v} \rVert}\) y lo multiplicamos por la longitud de la proyección. En otras palabras,\[\operatorname{proj}_{\vec{v}}(\vec{w}) = (\cos \theta) \lVert \vec{w} \rVert \frac{\vec{v}}{\lVert \vec{v} \rVert} = \frac{(\cos \theta) \lVert \vec{w} \rVert \lVert \vec{v} \rVert}{ {\lVert \vec{v} \rVert}^2 } \vec{v} = \frac{\langle \vec{w}, \vec{v} \rangle}{ \langle \vec{v}, \vec{v} \rangle } \vec{v} . \nonumber \]

Ejemplo\(\PageIndex{2}\)

Supongamos que deseamos proyectar el vector\((3,2,1)\) sobre el vector\((1,2,3)\). Computar\[\begin{align}\begin{aligned} \operatorname{proj}_{(1,2,3)} \bigl( (3,2,1) \bigr) = \frac{\langle (3,2,1) , (1,2,3) \rangle}{\langle (1,2,3) , (1,2,3) \rangle} (1,2,3) & = \frac{3 \cdot 1 + 2 \cdot 2 + 1 \cdot 3}{ 1 \cdot 1 + 2 \cdot 2 + 3 \cdot 3} (1,2,3) \\ & = \frac{10}{14} (1,2,3) = \left(\frac{5}{7},\frac{10}{7},\frac{15}{7}\right) . \end{aligned}\end{align} \nonumber \] Comprobemos dos veces que la proyección es ortogonal. Eso\(\vec{w}-\operatorname{proj}_{\vec{v}}(\vec{w})\) debe ser ortogonal a\(\vec{v}\), ver el ángulo recto en la Figura\(\PageIndex{2}\). Es decir,\[(3,2,1) - \operatorname{proj}_{(1,2,3)} \bigl( (3,2,1) \bigr) = \left(3-\frac{5}{7},2-\frac{10}{7},1-\frac{15}{7}\right) = \left(\frac{16}{7},\frac{4}{7},\frac{-8}{7}\right) \nonumber \] debe ser ortogonal a\((1,2,3)\). Calculamos el producto interno y es mejor que obtengamos cero:\[\left\langle \left(\frac{16}{7},\frac{4}{7},\frac{-8}{7}\right) , (1,2,3) \right\rangle = \frac{16}{7} \cdot 1 + \frac{4}{7} \cdot 2 -\frac{8}{7} \cdot 3 = 0 . \nonumber \]

Bases ortogonales

Como dijimos, una base\(\vec{v}_1,\vec{v}_2,\ldots,\vec{v}_n\) es una base ortogonal si todos los vectores en la base son ortogonales entre sí, es decir, si\[\langle \vec{v}_j , \vec{v}_k \rangle = 0 \nonumber \] para todas las elecciones de\(j\) y\(k\) dónde\(j \not= k\) (un vector distinto de cero no puede ser ortogonal a sí mismo). Una base se llama además una base ortonormal si todos los vectores en una base también son vectores unitarios, es decir, si todos los vectores tienen magnitud 1. Por ejemplo, la base estándar\(\{ (1,0,0), (0,1,0), (0,0,1) \}\) es una base ortonormal de\({\mathbb{R}}^3\): Cualquier par es ortogonal, y cada vector es de magnitud unitaria.

La razón por la que nos interesan las bases ortogonales (u ortonormales) es que hacen que sea realmente sencillo representar un vector (o una proyección sobre un subespacio) en la base. La fórmula simple para la proyección ortogonal sobre un vector nos da los coeficientes. En el Capítulo 4, utilizamos la misma idea al encontrar la base ortogonal correcta para el conjunto de soluciones de una ecuación diferencial. Entonces podemos encontrar cualquier solución en particular simplemente aplicando la fórmula de proyección ortogonal, que es solo un par de productos internos.

Volvamos al álgebra lineal. Supongamos que tenemos un subespacio y una base ortogonal\(\vec{v}_1, \vec{v}_2, \ldots, \vec{v}_n\). Deseamos expresarnos\(\vec{x}\) en términos de la base. Si no\(\vec{x}\) está en el lapso de la base (cuando no está en el subespacio dado), entonces por supuesto que no es posible, pero la siguiente fórmula nos da al menos la proyección ortogonal sobre el subespacio, o en otras palabras, la mejor aproximación en el subespacio.

Primero supongamos que\(\vec{x}\) está en el lapso. Entonces es la suma de las proyecciones ortogonales:\[\vec{x} = \operatorname{proj}_{\vec{v}_1} ( \vec{x} ) + \operatorname{proj}_{\vec{v}_2} ( \vec{x} ) + \cdots + \operatorname{proj}_{\vec{v}_n} ( \vec{x} ) = \frac{\langle \vec{x}, \vec{v}_1 \rangle}{ \langle \vec{v}_1, \vec{v}_1 \rangle } \vec{v}_1 + \frac{\langle \vec{x}, \vec{v}_2 \rangle}{ \langle \vec{v}_2, \vec{v}_2 \rangle } \vec{v}_2 + \cdots + \frac{\langle \vec{x}, \vec{v}_n \rangle}{ \langle \vec{v}_n, \vec{v}_n \rangle } \vec{v}_n . \nonumber \] En otras palabras, si queremos escribir\(\vec{x} = a_1 \vec{v}_1 + a_2 \vec{v}_2 + \cdots + a_n \vec{v}_n\), entonces\[a_1 = \frac{\langle \vec{x}, \vec{v}_1 \rangle}{ \langle \vec{v}_1, \vec{v}_1 \rangle } , \quad a_2 = \frac{\langle \vec{x}, \vec{v}_2 \rangle}{ \langle \vec{v}_2, \vec{v}_2 \rangle } , \quad \ldots , \quad a_n = \frac{\langle \vec{x}, \vec{v}_n \rangle}{ \langle \vec{v}_n, \vec{v}_n \rangle } . \nonumber \] Otra forma de derivar esta fórmula es trabajar a la inversa. Supongamos que\(\vec{x} = a_1 \vec{v}_1 + a_2 \vec{v}_2 + \cdots + a_n \vec{v}_n\). Tomar un producto interno con\(\vec{v}_j\), y utilizar las propiedades del producto interno:\[\begin{align}\begin{aligned} \langle \vec{x} , \vec{v}_j \rangle & = \langle a_1 \vec{v}_1 + a_2 \vec{v}_2 + \cdots + a_n \vec{v}_n , \vec{v}_j \rangle \\ & = a_1 \langle \vec{v}_1 , \vec{v}_j \rangle + a_2 \langle \vec{v}_2 , \vec{v}_j \rangle + \cdots + a_n \langle \vec{v}_n , \vec{v}_j \rangle . \end{aligned}\end{align} \nonumber \] Como la base es ortogonal, entonces\(\langle \vec{v}_k , \vec{v}_j \rangle = 0\) cuando sea\(k \not= j\). Eso quiere decir que solo uno de los términos, el\(j^{\text{th}}\) uno, del lado derecho es distinto de cero y obtenemos\[\langle \vec{x} , \vec{v}_j \rangle = a_j \langle \vec{v}_j , \vec{v}_j \rangle . \nonumber \] Resolviendo para\(a_j\) lo encontramos\(a_j = \frac{\langle \vec{x}, \vec{v}_j \rangle}{ \langle \vec{v}_j, \vec{v}_j \rangle }\) como antes.

Ejemplo\(\PageIndex{3}\)

Los vectores\((1,1)\) y\((1,-1)\) forman una base ortogonal de\({\mathbb{R}}^2\). Supongamos que deseamos representar\((3,4)\) en términos de esta base, es decir, deseamos encontrar\(a_1\) y\(a_2\) tal que\[(3,4) = a_1 (1,1) + a_2 (1,-1) . \nonumber \] calculamos:\[a_1 = \frac{\langle (3,4), (1,1) \rangle}{ \langle (1,1), (1,1) \rangle } = \frac{7}{2}, \qquad a_2 = \frac{\langle (3,4), (1,-1) \rangle}{ \langle (1,-1), (1,-1) \rangle } = \frac{-1}{2} . \nonumber \] Así\[(3,4) = \frac{7}{2} (1,1) + \frac{-1}{2} (1,-1) . \nonumber \]

Si la base es ortonormal en lugar de ortogonal, entonces todos los denominadores son uno. Es fácil hacer una base ortonormal—dividir todos los vectores por su tamaño. Si quieres descomponer muchos vectores, puede ser mejor encontrar una base ortonormal. En el ejemplo anterior, la base ortonormal que así crearíamos es\[\left( \frac{1}{\sqrt{2}} , \frac{1}{\sqrt{2}} \right) , \quad \left( \frac{1}{\sqrt{2}} , \frac{-1}{\sqrt{2}} \right) . \nonumber \] Entonces el cálculo habría sido\[\begin{align}\begin{aligned} (3,4) & = \left\langle (3,4) , \left( \frac{1}{\sqrt{2}} , \frac{1}{\sqrt{2}} \right) \right\rangle \left( \frac{1}{\sqrt{2}} , \frac{1}{\sqrt{2}} \right) + \left\langle (3,4) , \left( \frac{1}{\sqrt{2}} , \frac{-1}{\sqrt{2}} \right) \right\rangle \left( \frac{1}{\sqrt{2}} , \frac{-1}{\sqrt{2}} \right) \\ & = \frac{7}{\sqrt{2}} \left( \frac{1}{\sqrt{2}} , \frac{1}{\sqrt{2}} \right) + \frac{-1}{\sqrt{2}} \left( \frac{1}{\sqrt{2}} , \frac{-1}{\sqrt{2}} \right) . \end{aligned}\end{align} \nonumber \] Tal vez el ejemplo no es tan inspirador, pero dado vectores en\({\mathbb{R}}^{20}\) lugar de\({\mathbb{R}}^2\), entonces seguramente uno preferiría hacer 20 productos internos (o 40 si no tuviéramos un ortonormal) en lugar de resolver un sistema de veinte ecuaciones en veinte incógnitas usando reducción de fila de una\(20 \times 21\) matriz.

Como dijimos anteriormente, la fórmula sigue funcionando aunque no\(\vec{x}\) esté en el subespacio, aunque entonces no nos consigue el vector\(\vec{x}\) sino su proyección. Más concretamente, supongamos que\(S\) es un subespacio que es el lapso de\(\vec{v}_1,\vec{v}_2,\ldots,\vec{v}_n\) y\(\vec{x}\) es cualquier vector. Dejar\(\operatorname{proj}_{S}(\vec{x})\) ser el vector en el\(S\) que es el más cercano a\(\vec{x}\). Entonces Por\[\operatorname{proj}_{S}(\vec{x}) = \frac{\langle \vec{x}, \vec{v}_1 \rangle}{ \langle \vec{v}_1, \vec{v}_1 \rangle } \vec{v}_1 + \frac{\langle \vec{x}, \vec{v}_2 \rangle}{ \langle \vec{v}_2, \vec{v}_2 \rangle } \vec{v}_2 + \cdots + \frac{\langle \vec{x}, \vec{v}_n \rangle}{ \langle \vec{v}_n, \vec{v}_n \rangle } \vec{v}_n . \nonumber \] supuesto, si\(\vec{x}\) está en\(S\), entonces\(\operatorname{proj}_{S}(\vec{x}) = \vec{x}\), como el vector más cercano en\(S\) a\(\vec{x}\) es en\(\vec{x}\) sí mismo. Pero la verdadera utilidad se obtiene cuando no\(\vec{x}\) está en\(S\). En gran parte de las matemáticas aplicadas, no podemos encontrar una solución exacta a un problema, pero tratamos de encontrar la mejor solución a partir de un pequeño subconjunto (subespacio). Las sumas parciales de las series de Fourier del Capítulo 4 son un ejemplo. Otro ejemplo es la aproximación de mínimos cuadrados para ajustar una curva a los datos. Otro ejemplo es dado por los métodos numéricos más utilizados para resolver ecuaciones diferenciales parciales, los métodos de elementos finitos.

Ejemplo\(\PageIndex{4}\)

Los vectores\((1,2,3)\) y\((3,0,-1)\) son ortogonales, y así son una base ortogonal de un subespacio\(S\):\[S = \operatorname{span} \bigl\{ (1,2,3), (3,0,-1) \bigr\} . \nonumber \] Encontremos el vector en el\(S\) que está más cerca\((2,1,0)\). Es decir, encontremos\(\operatorname{proj}_{S}\bigl((2,1,0)\bigr)\). \[\begin{align}\begin{aligned} \operatorname{proj}_{S}\bigl((2,1,0)\bigr) & = \frac{\langle (2,1,0), (1,2,3) \rangle}{ \langle (1,2,3), (1,2,3) \rangle } (1,2,3) + \frac{\langle (2,1,0), (3,0,-1) \rangle}{ \langle (3,0,-1), (3,0,-1) \rangle } (3,0,-1) \\ & = \frac{2}{7} (1,2,3) + \frac{3}{5} (3,0,-1) \\ &= \left( \frac{73}{35} , \frac{4}{7} , \frac{9}{35} \right) . \end{aligned}\end{align} \nonumber \]

Proceso Gram—Schmidt

Antes de dejar las bases ortogonales, anotemos un procedimiento para fabricarlas a partir de cualquier base antigua. Puede que no sea difícil llegar a una base ortogonal para un subespacio bidimensional, pero para un subespacio de 20 dimensiones, parece una tarea desalentadora. Afortunadamente, la proyección ortogonal puede ser utilizada para “proyectar lejos” los bits de los vectores que los están haciendo no ortogonales. Se llama el proceso Gram-Schmidt.

Comenzamos con una base de vectores\(\vec{v}_1,\vec{v}_2, \ldots, \vec{v}_n\). Construimos una base ortogonal de la\(\vec{w}_1, \vec{w}_2, \ldots, \vec{w}_n\) siguiente manera. \[\begin{align}\begin{aligned} \vec{w}_1 & = \vec{v}_1 , \\ \vec{w}_2 & = \vec{v}_2 - \operatorname{proj}_{\vec{w}_1}(\vec{v}_2) , \\ \vec{w}_3 & = \vec{v}_3 - \operatorname{proj}_{\vec{w}_1}(\vec{v}_3) - \operatorname{proj}_{\vec{w}_2}(\vec{v}_3) , \\ \vec{w}_4 & = \vec{v}_4 - \operatorname{proj}_{\vec{w}_1}(\vec{v}_4) - \operatorname{proj}_{\vec{w}_2}(\vec{v}_4) - \operatorname{proj}_{\vec{w}_3}(\vec{v}_4) , \\ & \vdots \\ \vec{w}_n & = \vec{v}_n - \operatorname{proj}_{\vec{w}_1}(\vec{v}_n) - \operatorname{proj}_{\vec{w}_2}(\vec{v}_n) - \cdots - \operatorname{proj}_{\vec{w}_{n-1}}(\vec{v}_n) .\end{aligned}\end{align} \nonumber \]Lo que hacemos es en el\(k^{\text{th}}\) paso, tomamos\(\vec{v}_k\) y restamos la proyección de\(\vec{v}_k\) al subespacio abarcado por\(\vec{w}_1,\vec{w}_2,\ldots,\vec{w}_{k-1}\).

Ejemplo\(\PageIndex{5}\)

Considere los vectores\((1,2,-1)\), y\((0,5,-2)\) y llame\(S\) al lapso de los dos vectores. Encontremos una base ortogonal de\(S\):\[\begin{align}\begin{aligned} \vec{w}_1 & = (1,2,-1) , \\ \vec{w}_2 & = (0,5,-2) - \operatorname{proj}_{(1,2,-1)}\bigl((0,2,-2)\bigr) \\ & = (0,1,-1) - \frac{\langle (0,5,-2), (1,2,-1) \rangle}{ \langle (1,2,-1), (1,2,-1) \rangle } (1,2,-1) = (0,5,-2) - 2 (1,2,-1) = (-2,1,0) .\end{aligned}\end{align} \nonumber \] Así\((1,2,-1)\) y\((-2,1,0)\) span\(S\) y son ortogonales. Comprobemos:\(\langle (1,2,-1) , (-2,1,0) \rangle = 0\).

Supongamos que deseamos encontrar una base ortonormal, no sólo ortogonal. Bueno, simplemente hacemos los vectores en vectores unitarios dividiéndolos por su magnitud. Los dos vectores que componen la base ortonormal de\(S\) son:\[\frac{1}{\sqrt{6}} (1,2,-1) = \left( \frac{1}{\sqrt{6}}, \frac{2}{\sqrt{6}}, \frac{-1}{\sqrt{6}} \right) , \qquad \frac{1}{\sqrt{5}} (-2,1,0) = \left( \frac{-2}{\sqrt{5}}, \frac{1}{\sqrt{5}}, 0 \right) . \nonumber \]

Notas al pie

[1] Cuando Euclides definió ángulos en sus Elementos, el único ángulo que definió realmente fue el ángulo recto.