6.1: Problemas de Primavera I
- Page ID
- 115008
Consideramos el movimiento de un objeto de masa\(m\), suspendido de un resorte de masa insignificante. Decimos que el sistema muelle—masa está en equilibrio cuando el objeto está en reposo y las fuerzas que actúan sobre él suman cero. La posición del objeto en este caso es la posición de equilibrio. \(y\)Definimos como el desplazamiento del objeto desde su posición de equilibrio (Figura 6.1.1 ), medido positivo hacia arriba.
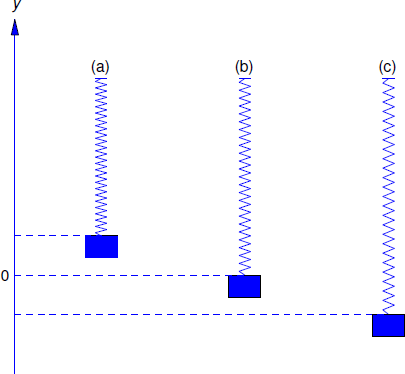
Nuestro modelo da cuenta de los siguientes tipos de fuerzas que actúan sobre el objeto:
- La fuerza\(-mg\), debido a la gravedad.
- Una fuerza\(F_s\) ejercida por el resorte resistiendo el cambio en su longitud. La longitud natural del resorte es su longitud sin masa unida. Suponemos que el resorte obedece a la ley de Hooke: Si la longitud del resorte se cambia en una cantidad\(\Delta L\) de su longitud natural, entonces el resorte ejerce una fuerza\(F_s=k\Delta L\), donde\(k\) hay un número positivo llamado constante de resorte. Si el resorte se estira entonces\(\Delta L>0\) y\(F_s>0\), entonces la fuerza del resorte es hacia arriba, mientras que si el resorte se comprime entonces\(\Delta L<0\) y\(F_s<0\), entonces la fuerza del resorte es hacia abajo.
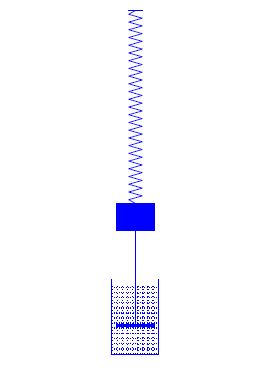
- Una fuerza de amortiguación\(F_d=-cy'\) que resiste el movimiento con una fuerza proporcional a la velocidad del objeto. Puede deberse a la resistencia al aire o a la fricción en el resorte. Sin embargo, una manera conveniente de visualizar una fuerza de amortiguación es asumir que el objeto está rígidamente unido a un pistón con una masa insignificante sumergida en un cilindro (llamado amortiguador) lleno de un líquido viscoso (Figura 6.1.1 ). A medida que el pistón se mueve, el líquido ejerce una fuerza de amortiguación. Decimos que el movimiento está sin amortiguar si\(c=0\), o amortiguado si\(c>0\).
- Una fuerza externa\(F\), distinta de la fuerza debida a la gravedad, que puede variar con\(t\), pero es independiente del desplazamiento y la velocidad. Decimos que la moción es libre si\(F\equiv0\), o forzada si\(F\not\equiv0\).
De la segunda ley de movimiento de Newton,
\[\label{eq:6.1.1} my''=-mg+F_d+F_s+F=-mg-cy'+F_s+F.\]
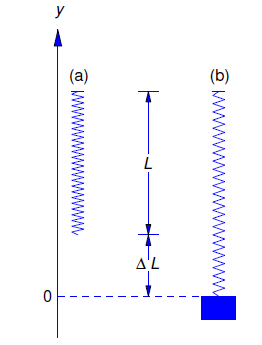
Ahora debemos\(F_s\) relacionarnos con\(y\). En ausencia de fuerzas externas el objeto estira el resorte en una cantidad\(\Delta l\) para asumir su posición de equilibrio (Figura 6.1.3 ). Dado que la suma de las fuerzas que actúan sobre el objeto es entonces cero, la Ley de Hooke implica eso\(mg=k\Delta l\). Si el objeto es desplazado\(y\) unidades de su posición de equilibrio, el cambio total en la longitud del resorte es\(\Delta L=\Delta l-y\), por lo que la ley de Hooke implica que
\[F_s=k\Delta L=k\Delta l-ky.\nonumber \]
Sustituyendo esto en la ecuación\ ref {eq:6.1.1} rendimientos
\[my''=-mg-cy'+k\Delta L-ky+F.\nonumber \]
Ya que\(mg=k\Delta l\) esto se puede escribir como
\[\label{eq:6.1.2} my''+cy'+ky=F.\]
A esto lo llamamos la ecuación del movimiento.
Movimiento armónico simple
A lo largo del resto de esta sección consideraremos sistemas de muelle—masa sin amortiguación; es decir,\(c=0\). Consideraremos sistemas con amortiguación en la siguiente sección. Primero consideramos el caso donde la moción también es libre; es decir,\(F\) =0. Comenzamos con un ejemplo.
Un objeto estira un resorte\(6\) pulgadas en equilibrio.
- Configura la ecuación de movimiento y encuentra su solución general.
- Encuentra el desplazamiento del objeto para\(t>0\) si inicialmente se desplaza 18 pulgadas por encima del equilibrio y se le da una velocidad descendente de\(3\) pies/s.
Solución a:
Ajuste\(c=0\) y\(F=0\) en Ecuación\ ref {eq:6.1.2} produce la ecuación de movimiento
\[my''+ky=0,\nonumber \]
que reescribimos como
\[\label{eq:6.1.3} y''+{k\over m}y=0.\]
Aunque necesitaríamos el peso del objeto para obtener\(k\) de la ecuación\(mg=k\Delta l\) podemos obtener\(k/m\) de\(\Delta l\) solos; así,\(k/m=g/\Delta l\). Consistente con las unidades utilizadas en la declaración del problema, tomamos\(g=32\) pies/s\(^2\). Aunque\(\Delta l\) se indica en pulgadas, debemos convertirlo en pies para que sea consistente con esta elección de\(g\); es decir,\(\Delta l =1/2\) ft. Por lo tanto
\[{k\over m}={32\over1/2}=64\nonumber \]
y la Ecuación\ ref {eq:6.1.3} se convierte
\[\label{eq:6.1.4} y''+64y=0.\]
La ecuación característica de la Ecuación\ ref {eq:6.1.4} es
\[r^2+64=0,\nonumber \]
que tiene los ceros\(r=\pm 8i\). Por lo tanto, la solución general de la Ecuación\ ref {eq:6.1.4} es
\[\label{eq:6.1.5} y=c_1\cos8t+c_2\sin8t.\]
Solución b:
El desplazamiento inicial hacia arriba de 18 pulgadas es positivo y debe expresarse en pies. La velocidad inicial hacia abajo es negativa; por lo tanto,
\[y(0)={3\over2}\quad \text{and} \quad y'(0)=-3.\nonumber \]
Ecuación diferenciadora\ ref {eq:6.1.5} rendimientos
\[\label{eq:6.1.6} y'=-8c_1\sin8t+8c_2\cos8t.\]
Establecer\(t=0\) en Ecuación\ ref {eq:6.1.5} y Ecuación\ ref {eq:6.1.6} e imponer las condiciones iniciales muestra que\(c_1=3/2\) y\(c_2=-3/8\). Por lo tanto
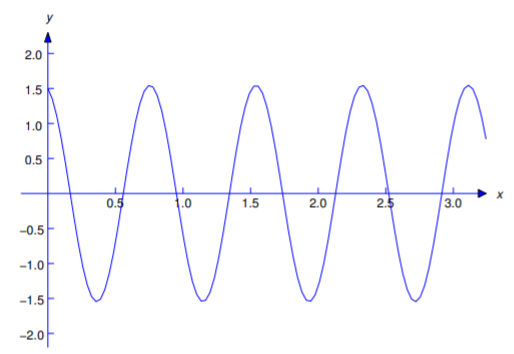
\[y={3\over2}\cos8t-{3\over8}\sin8t,\nonumber \]
donde\(y\) está en pies (Figura 6.1.4 ).
Ahora consideraremos la ecuación
\[my''+ky=\nonumber 0\]
donde\(m\) y\(k\) son números positivos arbitrarios. Dividir por\(m\) y definir\(\omega_0=\sqrt{k/m}\) rendimientos
\[y''+\omega_0^2y=0.\nonumber \]
La solución general de esta ecuación es
\[\label{eq:6.1.7} y=c_1\cos\omega_0t+c_2\sin\omega_0t.\]
Podemos reescribir esto de una forma más útil definiendo
\[\label{eq:6.1.8} R=\sqrt{c_1^2+c_2^2},\]
y
\[\label{eq:6.1.9} c_1=R\cos\phi\quad \text{and} \quad c_2=R\sin\phi.\]
Sustituir de la ecuación\ ref {eq:6.1.9} a la ecuación\ ref {eq:6.1.7} y aplicar la identidad
\[\cos\omega_0t\cos\phi+\sin\omega_0t\sin\phi=\cos(\omega_0t-\phi)\nonumber \]
rendimientos
\[\label{eq:6.1.10} y=R\cos(\omega_0t-\phi).\]
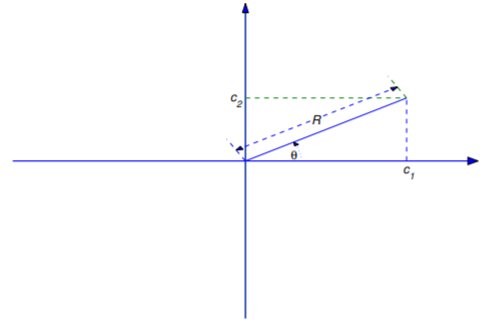
De la Ecuación\ ref {eq:6.1.8} y Ecuación\ ref {eq:6.1.9} vemos que el\(R\) y se\(\phi\) puede interpretar como coordenadas polares del punto con coordenadas rectangulares\((c_1,c_2)\) (Figura 6.1.5 ). Dado\(c_1\) y\(c_2\), podemos calcular\(R\) a partir de la Ecuación\ ref {eq:6.1.8}. De la Ecuación\ ref {eq:6.1.8} y la Ecuación\ ref {eq:6.1.9}, vemos que\(\phi\) está relacionado con\(c_1\) y\(c_2\) por
\[\cos\phi={c_1\over\sqrt{c_1^2+c_2^2}}\quad \text{and} \quad\sin\phi= {c_2\over\sqrt{c_1^2+c_2^2}}.\nonumber \]
Hay infinitamente muchos ángulos\(\phi\), que difieren por múltiplos enteros de\(2\pi\), que satisfacen estas ecuaciones. Siempre vamos a elegir\(\phi\) para que\(-\pi\le\phi<\pi\).
El movimiento descrito por la Ecuación\ ref {eq:6.1.7} o Ecuación\ ref {eq:6.1.10} es simple movimiento armónico. Vemos de cualquiera de estas ecuaciones que el movimiento es periódico, con punto
\[T=2\pi/\omega_0.\nonumber \]
Este es el tiempo requerido para que el objeto complete un ciclo completo de oscilación (por ejemplo, para pasar de su posición más alta a su posición más baja y de regreso a su posición más alta). Ya que las posiciones más altas y más bajas del objeto son\(y=R\) y\(y=-R\), decimos que\(R\) es la amplitud de la oscilación. El ángulo\(\phi\) en la Ecuación\ ref {eq:6.1.10} es el ángulo de fase. Se mide en radianes. Ecuación La ecuación\ ref {eq:6.1.10} es la forma de amplitud—fase del desplazamiento. Si\(t\) es en segundos entonces\(\omega_0\) está en radianes por segundo (rad/s); es la frecuencia del movimiento. También se le llama la frecuencia natural del sistema de muelle—masa sin amortiguación.
Encontramos que el desplazamiento del objeto en Ejemplo 6.1.1 es
\[y={3\over2}\cos8t-{3\over8}\sin8t.\nonumber \]
Encuentra la frecuencia, el período, la amplitud y el ángulo de fase del movimiento.
Solución:
La frecuencia es\(\omega_0=8\) rad/s, y el periodo es\(T=2\pi/\omega_0=\pi/4\) s. Desde\(c_1=3/2\) y\(c_2=-3/8\), la amplitud es
\[R=\sqrt{c^2_1+c^2_2}=\sqrt{\left({3\over2}\right)^2+\left({3\over8}\right)^2} ={3\over8}\sqrt{17}.\nonumber \]
El ángulo de fase está determinado por
\[\label{eq:6.1.11} \cos\phi = \frac{\frac{3}{2}}{\frac{3}{8}\sqrt{17}} = \frac{4}{\sqrt{17}}\]
y\[\label{eq:6.1.12} \sin\phi={-{3\over8}\over{3\over8}\sqrt{17}}=-{1\over\sqrt{17}}.\]
Usando una calculadora, vemos en la Ecuación\ ref {eq:6.1.11} que\[\phi\approx\pm.245\mbox{ rad}.\nonumber \]
Dado que\(\sin\phi<0\) (ver Ecuación\ ref {eq:6.1.12}), aquí se aplica el signo menos; es decir,\[\phi\approx-.245\mbox{ rad}.\nonumber \]
La longitud natural de un resorte es de 1 m. Un objeto se une a él y la longitud del resorte aumenta a 102 cm cuando el objeto está en equilibrio. Entonces el objeto se desplaza inicialmente hacia abajo 1 cm y se le da una velocidad ascendente de 14 cm/s\(t>0\). Además, encuentre la frecuencia natural, el período, la amplitud y el ángulo de fase del movimiento resultante. Exprese las respuestas en unidades cgs.
Solución:
En unidades cgs\(g=980\) cm/s\(^2\). Desde\(\Delta l=2\) cm,\(\omega_0^2=g/\Delta l=490\). Por lo tanto
\[y''+490y=0, \quad y(0)=-1,\quad y'(0)=14.\nonumber \]
La solución general de la ecuación diferencial es\[y=c_1\cos7\sqrt{10}t+c_2\sin7\sqrt{10}t,\nonumber \]
por lo\[y'=7\sqrt{10}\left(-c_1\sin7\sqrt{10}t+c_2\cos7\sqrt{10}t\right).\nonumber \]
Sustituir las condiciones iniciales en las dos últimas ecuaciones arroja\(c_1=-1\) y\(c_2=2/\sqrt{10}\). Por lo tanto,\[y=-\cos7\sqrt{10}t+{2\over\sqrt{10}}\sin7\sqrt{10}t.\nonumber \]
La frecuencia es\(7\sqrt{10}\) rad/s, y el periodo es\(T=2\pi/(7\sqrt{10})\) s. La amplitud es
\[R=\sqrt{c_{1}^{2}+c_{2}^{2}}=\sqrt{(-1)^{2}+\left(\frac{2}{\sqrt{10}} \right)^{2}}=\sqrt{\frac{7}{5}}\text{cm}\nonumber \]
El ángulo de fase está determinado por
\[\cos\phi = \frac{c_{1}}{R}=-\sqrt{\frac{5}{7}}\quad\text{and}\quad\sin\phi = \frac{c_{2}}{R}=\sqrt{\frac{2}{7}}\nonumber \]
Por lo tanto\(\phi\) está en el segundo cuadrante y
\[\phi = \cos ^{-1}\left(-\sqrt{\frac{5}{7}} \right)\approx 2.58\text{rad}\nonumber \]
Oscilación forzada sin amortiguar
En muchos problemas mecánicos, un dispositivo está sometido a fuerzas externas periódicas. Por ejemplo, los soldados que marchan cadencia en un puente provocan perturbaciones periódicas en el puente, y los motores de un avión impulsado por hélice provocan perturbaciones periódicas en sus alas. En ausencia de fuerzas de amortiguación suficientes, tales perturbaciones —aunque sean pequeñas en magnitud— pueden causar averías estructurales si se encuentran en ciertas frecuencias críticas. Para ilustrar esto, consideraremos el movimiento de un objeto en un sistema de muelle—masa sin amortiguación, sujeto a una fuerza externa
\[F(t)=F_0\cos\omega t\nonumber \]
donde\(F_0\) es una constante. En este caso la ecuación de movimiento Ecuación\ ref {eq:6.1.2} es
\[my''+ky=F_0\cos\omega t,\nonumber \]
que reescribimos como
\[\label{eq:6.1.13} y''+\omega_0^2y={F_0\over m}\cos\omega t\]
con\(\omega_0=\sqrt{k/m}\). Veremos a partir de los siguientes dos ejemplos que las soluciones de Ecuación\ ref {eq:6.1.13} con\(\omega\ne\omega_0\) se comportan de manera muy diferente a las soluciones con\(\omega=\omega_0\).
Resolver el problema de valor inicial
\[\label{eq:6.1.14} y''+\omega_0^2y={F_0\over m}\cos\omega t, \quad y(0)=0,\quad y'(0)=0,\]
dado eso\(\omega\ne\omega_0\).Solución:
Primero obtenemos una solución particular de la Ecuación\ ref {eq:6.1.13} por el método de coeficientes indeterminados. Ya que\(\omega\ne\omega _0\),\(\cos\omega t\) no es una solución de la ecuación complementaria
\[y''+\omega_0^2y=0.\nonumber \]
Por lo tanto, la ecuación\ ref {eq:6.1.13} tiene una solución particular de la forma\[y_p=A\cos\omega t+B\sin\omega t.\nonumber \]
Desde\[y''_p=-\omega^2(A\cos\omega t+B\sin\omega t),\nonumber \]
\[y_p''+\omega_0^2y_p={F_0\over m}\cos\omega t\nonumber \]
si y solo si\[(\omega_0^2-\omega^2)\left(A\cos\omega t+ B\sin\omega t\right)={F_0\over m}\cos\omega t.\nonumber \]
Esto se mantiene si y solo si\[A={F_0\over m(\omega_0^2-\omega^2)}\quad \text{and} \quad B=0,\nonumber \]
por lo\[y_p={F_0\over m(\omega_0^2-\omega^2)}\cos\omega t.\nonumber \]
La solución general de la Ecuación\ ref {eq:6.1.13} es\[\label{eq:6.1.15} y={F_0\over m(\omega_0^2-\omega^2)}\cos\omega t +c_1\cos\omega_0 t+c_2\sin\omega_0t,\]
por lo\[y'={-\omega F_0\over m(\omega_0^2-\omega^2)}\sin\omega t +\omega_0(-c_1\sin\omega_0 t+c_2\cos\omega_0t).\nonumber \]
Las condiciones iniciales\(y(0)=0\) y\(y'(0)=0\) en la Ecuación\ ref {eq:6.1.14} implican que\[c_1=-{F_0\over m(\omega_0^2-\omega^2)}\quad \text{and} \quad c_2=0.\nonumber \]
Sustituyendo estos en Ecuación\ ref {eq:6.1.15} rendimientos\[\label{eq:6.1.16} y={F_0\over m(\omega_0^2-\omega^2)}(\cos\omega t-\cos\omega _0t).\]
Es revelador escribir esto en una forma diferente. Comenzamos con las identidades trigonométricas
\[\begin{aligned} \cos(\alpha-\beta)&=\cos\alpha\cos\beta+\sin\alpha\sin\beta\\ \cos(\alpha+\beta)&=\cos\alpha\cos\beta-\sin\alpha\sin\beta.\end{aligned}\nonumber \]
Restar la segunda identidad de los primeros rendimientos\[\label{eq:6.1.17} \cos(\alpha-\beta)-\cos(\alpha+\beta)=2\sin\alpha\sin\beta\]
Ahora vamos\[\label{eq:6.1.18} \alpha-\beta=\omega t\quad \text{and} \quad\alpha+\beta=\omega_0t,\]
para que\[\label{eq:6.1.19} \alpha={(\omega_0+\omega)t\over2}\quad \text{and} \quad \beta={(\omega_0-\omega)t\over2}.\]
Sustituyendo la ecuación\ ref {eq:6.1.18} y la ecuación\ ref {eq:6.1.19} en la ecuación\ ref {eq:6.1.17} rendimientos\[\cos\omega t-\cos\omega_0t= 2\sin{(\omega_0-\omega)t\over2}\sin{(\omega_0+\omega)t\over2},\nonumber \]
y sustituyendo esto en Ecuación\ ref {eq:6.1.16} rendimientos\[\label{eq:6.1.20} y=R(t)\sin{(\omega_0+\omega)t\over2},\]
donde\[\label{eq:6.1.21} R(t)={2F_0\over m(\omega_0^2-\omega^2)} \sin{(\omega_0-\omega)t\over2}.\]
De la Ecuación\ ref {eq:6.1.20} podemos considerar\(y\) como una variación sinusoidal con frecuencia\((\omega_0+\omega)/2\) y amplitud variable\(|R(t)|\). En la Figura 6.1.6 la curva discontinua por encima del\(t\) eje es\(y=|R(t)|\), la curva discontinua debajo del\(t\) eje es\(y=-|R(t)|\), y el desplazamiento\(y\) aparece como una oscilación delimitada por ellos. La oscilación de\(y\) for\(t\) en un intervalo entre ceros sucesivos de\(R(t)\) se llama latido.
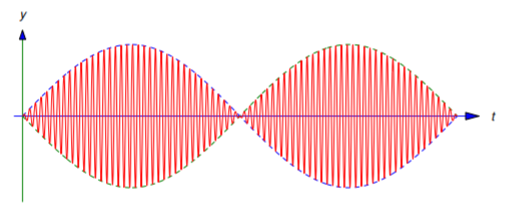
Se puede ver en la Ecuación\ ref {eq:6.1.20} y Ecuación\ ref {eq:6.1.21} que
\[|y(t)|\le{2|F_0|\over m|\omega_0^2-\omega^2|};\nonumber \]
además, si\(\omega+\omega_0\) es suficientemente grande en comparación con\(\omega -\omega_0\), entonces\(|y|\) asume valores cercanos a (quizás iguales a) este límite superior durante cada latido. Sin embargo, la oscilación permanece limitada para todos\(t\). (Esto supone que el resorte puede soportar deflexiones de este tamaño y seguir obedeciendo la ley de Hooke.) El siguiente ejemplo muestra que esto no es así si\(\omega=\omega_0\).
Encuentre la solución general de
\[\label{eq:6.1.22} y''+\omega_0^2y={F_0\over m}\cos\omega_0t.\]
Solución:
Primero obtenemos una solución particular\(y_p\) de la Ecuación\ ref {eq:6.1.22}. Dado que\(\cos\omega_0t\) es una solución de la ecuación complementaria, la forma para\(y_p\) es
\[\label{eq:6.1.23} y_p=t(A\cos\omega_0t+B\sin\omega_0t).\]
Entonces\[y_p'=A\cos\omega_0t+B\sin\omega_0t +\omega_0t(-A\sin\omega_0t+B\cos\omega_0t)\nonumber \]
y\[\label{eq:6.1.24} y''_p=2\omega_0(-A\sin\omega_0t +B\cos\omega_0t)-\omega_0^2t(A\cos\omega_0t+B\sin\omega_0t).\]
De la Ecuación\ ref {eq:6.1.23} y la Ecuación\ ref {eq:6.1.24}, vemos que\(y_p\) satisface la Ecuación\ ref {eq:6.1.22} si\[-2A\omega_0\sin\omega_0t+2B\omega_0\cos\omega_0t={F_0\over m} \cos\omega_0t;\nonumber \]
es decir, si\[A=0\quad \text{and} \quad B={F_0\over2m\omega_0}.\nonumber \]
Por lo tanto\[y_p={F_0t\over2m\omega_0}\sin\omega_0t\nonumber \]
es una solución particular de la Ecuación\ ref {eq:6.1.22}. La solución general de la Ecuación\ ref {eq:6.1.22} es\[y={F_0t\over2m\omega_0}\sin\omega_0t+c_1\cos\omega_0t+c_2\sin\omega_0t.\nonumber \]
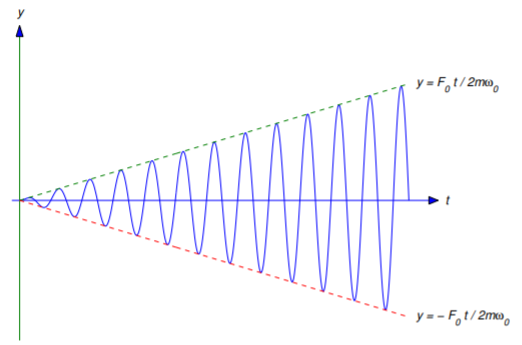
\[y={F_0t\over2m\omega_0}\quad \text{and} \quad y=-{F_0t\over2m\omega_0}\nonumber \]
con amplitud creciente que se aproxima\(\infty\) como\(t\to\infty\). Por supuesto, esto significa que la primavera finalmente debe dejar de obedecer la ley de Hooke o romperse.Este fenómeno de desplazamientos sin límites de un sistema muelle—masa en respuesta a una función de forzamiento periódico a su frecuencia natural se llama resonancia. Las estructuras mecánicas más complicadas también pueden exhibir fenómenos similares a la resonancia. Por ejemplo, las oscilaciones rítmicas de un puente colgante por fuerzas del viento o de un ala de un avión por vibraciones periódicas de motores alternativos pueden causar daños o incluso fallas si las frecuencias de las perturbaciones son cercanas a frecuencias críticas determinadas por los parámetros del sistema mecánico en pregunta.


