1.1: Introducción

Resolver ecuaciones diferenciales ordinarias

Resolver ecuaciones diferenciales ordinarias (ODEs) es un enfoque importante de la computación numérica. Comenzamos considerando las ODE de primer orden de la forma

\[\tag{eq:1.1} y' = f(t, y)\]

Dónde\(y(t)\) está lo desconocido (es decir, lo que queremos encontrar), y\(t\) es la variable independiente. Cuando se trata de una ODE de\(t\) este tipo, generalmente pensamos en el tiempo, y\(y\) como algo que depende del tiempo, como la población de una especie animal o la tensión de un nodo en un circuito electrónico. La ecuación [eq:1.1] dice que la forma en que\(y\) cambia en el tiempo depende de alguna función\(f\). En este folleto, asumimos que la función\(f\) es suave y de buen comportamiento, y que es fácilmente calculable en un programa de computadora.

Se pueden anotar soluciones a [eq:1.1], pero para obtener una solución única se requiere un dato adicional: Una condición inicial. Es decir, necesitamos saber algo\(y(t)\) en un momento dado para poder seleccionar una solución individual de todas las soluciones posibles que satisfagan [eq:1.1]. Tradicionalmente se usa un valor para\(y(t)\) en el tiempo\(t=0\) como condición inicial, pero también son posibles otras opciones (pero poco comunes).

He aquí un ejemplo muy básico. Considera la ODE Probablemente\[\tag{eq:1.2} y' = a y\] te encontraste con esta ODE al principio de tu carrera matemática, y conoces la solución de memoria:\[\tag{eq:1.3} y(t) = C e^{a t}\] donde\(C\) hay alguna constante. La solución [eq:1.3] obviamente satisface la ecuación [eq:1.2], pero no es útil en la práctica como solución a la ecuación. ¿Por qué? La razón es que hay un número infinito de posibles soluciones dependiendo del valor de los\(C\) elegidos. Es decir, [eq:1.3] define una familia de soluciones, pero en un problema real y práctico sólo queremos una de esas soluciones. Por ejemplo, ¿cómo harías una trama de [eq:1.3]? La respuesta es, no se puede, hasta que elija un valor específico de\(C\).

En un problema práctico, usualmente conoces el valor de tu función en un punto de inicio en el tiempo, casi siempre en\(t = 0\). Llama a ese valor\(y_0\). En este caso, la solución específica que satisface [eq:1.2] y también satisface\(y(t=0) = y_0\) es\[\tag{eq:1.4} y(t) = y_0 e^{a t}\] El punto es que resolver numéricamente una ODE requiere dos piezas de información: 1. La propia ODE, y 2. Una condición inicial. El valor inicial escoge una solución de toda la familia de soluciones que satisfacen [eq:1.2]. El concepto se muestra en 1.1

Figura 1.1: La ODE\(y' = f(t,y)\) es satisfecha por una familia de curvas. \(y(0)\)Se requiere una condición inicial para seleccionar una de las soluciones para simulación numérica.

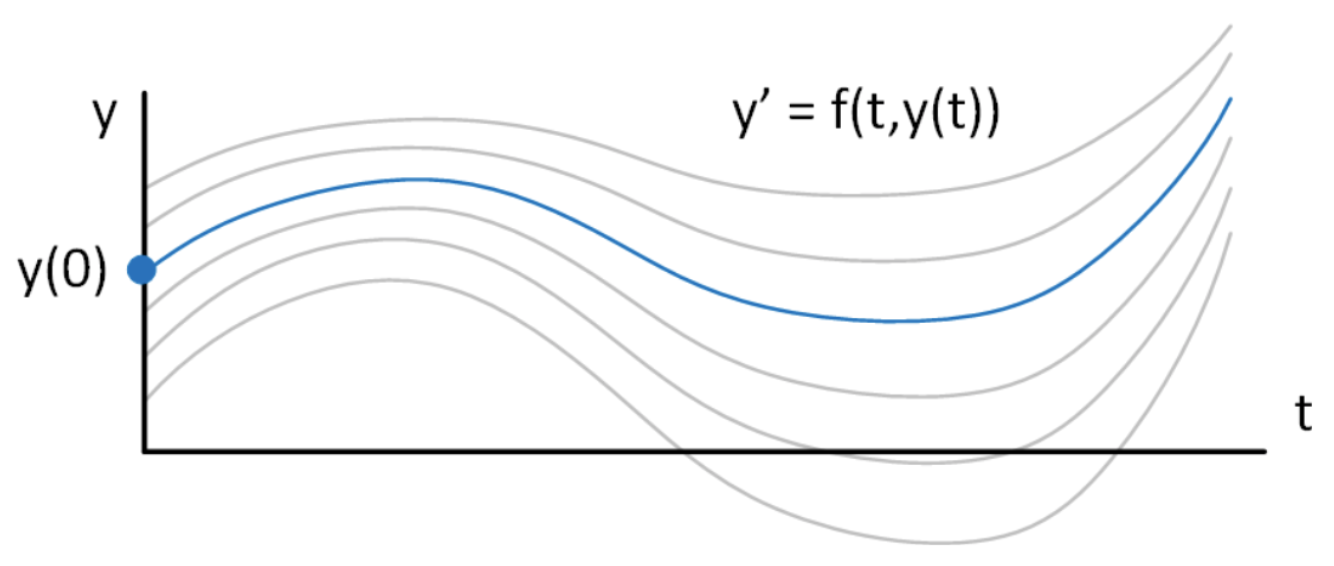
Tal problema se llama “problema de valor inicial” (IVP) para distinguirlo de otros tipos de ecuaciones diferenciales (que encontraremos más adelante en la clase). “Problema de valor inicial” simplemente significa que conocemos el valor inicial (inicial) de\(y\), y queremos encontrar su comportamiento a medida que avanzamos en el tiempo. Una vez que se especifica la ecuación [eq:1.1] y una condición inicial para\(y\), entonces tenemos toda la información requerida para encontrar una solución única\(y(t)\) numéricamente.

Los métodos para encontrar soluciones numéricas IVP son el foco de este folleto. Por cuestión de nomenclatura, generalmente decimos “resolver la ODE”, o “resolver el IVP”. Esto significa que calculamos la función a\(y(t)\) partir de tiempo\(t=0\) a algún momento en el futuro,\(t_{end}\). Otra forma de decir lo mismo es que “integramos la ODE”, o “integramos el IVP”. Al hablar de ODEs, “integrar” significa lo mismo que “resolver”.

Funciones muestreadas

En matemáticas nos familiarizamos con la noción de una función. Considere el caso más simple de una función\(y(t)\) que toma un escalar real\(t\) y devuelve un valor escalar real\(y(t)\). Esto con frecuencia se escribe formalmente como\(y:\mathbb{R}\rightarrow \mathbb{R}\). Esto significa, tomar cualquier número real arbitrario\(t\), enchufarlo y salir saldrá un nuevo número real\(y(t)\).\(y\) La idea importante a extraer de esto es que la función es como una máquina en la que se puede ingresar cualquiera\(t\) y esperar obtener una salida. Es decir, la función se define en cada número real\(t\).

Desafortunadamente, cuando se trabaja en datos reales usando una computadora esta bonita abstracción no siempre se sostiene. Más bien, es muy común que solo tengamos ciertos puntos discretos\(t_n\) donde se defina la función. El audio digital es un ejemplo sencillo: los sonidos que escuchamos con nuestro oído están relacionados con las ondas de presión sonora que mueven nuestros tímpanos. La presión sonora tiene un valor para cada punto en el tiempo. Pero cuando se procesa audio usando una computadora, la presión del sonido se muestrea en tiempos regulares y discretos y se convierte en números que representan la presión del sonido en cada tiempo de muestreo. Este proceso a menudo se conoce como “discretización”, lo que significa que el definido continuamente\(y(t)\) es reemplazado por un conjunto de muestras discretas\(y_n\). Esto se representa en 1.2, que muestra la relación de una función de tiempo continuo y su reemplazo de tiempo discreto (discretizado).

Figura 1.2: Una función muestreada. La versión de tiempo continuo de la función es\(y(t)\). El muestreo reemplaza\(y(t)\) con muestras tomadas en tiempos discretos,\(t_n\). Las muestras\(y_n\) pueden ser manejadas por la computadora como un vector o lista de valores. En el caso que se muestra aquí la función es muestreada a intervalos espaciados uniformemente separados por\(h\). Las muestras espaciadas uniformemente son el caso más frecuente; por ejemplo, el audio digital comúnmente muestrea una señal de sonido de entrada con un período\(h\) de aproximadamente 22.7usec (frecuencia de muestreo de 44.1kHz).

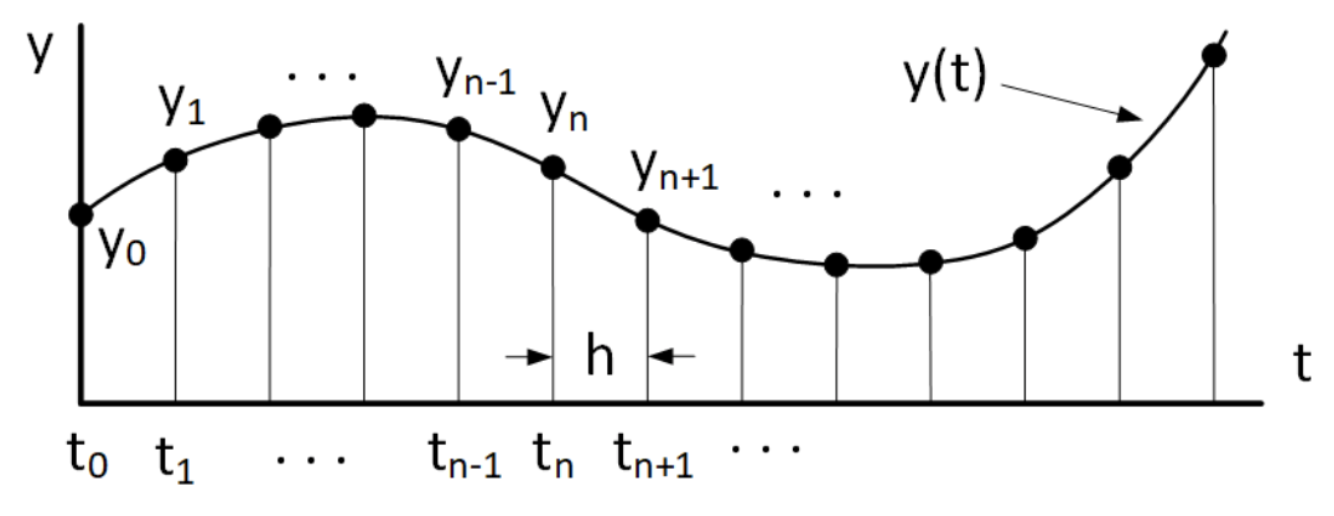
Resulta que los solucionadores de ODE vamos a estudiar todos los trabajos con funciones muestreadas. Es decir, los solucionadores computan la solución\(y(t)\) en una secuencia de valores discretos de tiempo\(t_n\) similares a la situación mostrada en 1.2. La salida del solucionador será un vector de valores discretos\(y_n\) que representan muestras de la función continua subyacente real\(y(t)\).

Aquí hay una sugerencia de implementación cuando escribe programas que procesan funciones muestreadas: La función muestreada en sí generalmente está representada por un vector,\(y_n\). Este es el objeto que su algoritmo utilizará durante su trabajo. Encima de\(y_n\) recomiendo llevar también alrededor un vector que represente los tiempos de muestreo,\(t_n\), en su programa. Tener tus tiempos de muestreo fácilmente accesibles puede ayudar a disminuir la confusión cuando quieres trazar\(y_n\) vs. tiempo, por ejemplo. Para vectores de tamaño moderado, la memoria extra requerida para retener\(t_n\) es un pequeño precio a pagar para mantener la confusión al mínimo mientras escribes tu código.

Diferenciación en la computadora

Siguiente antes de sumergirnos en la resolución [eq:1.1] necesitamos revisar cómo se hace la diferenciación en la computadora. Para comenzar, recuerda la definición de la derivada de la\(y(t)\) que probablemente aprendiste en la secundaria:\[\tag{eq:1.5} \frac{d y}{d t} = \lim_{{\Delta t}\to 0} \frac{y(t + \Delta t) - y(t)}{\Delta t}\] Al hacer computación numérica, no podemos representar la transición limitante\(\lim_{{\Delta t}\to 0}\); nuestros datos suelen ser discretos (por ejemplo, una función muestreada). Más importante aún, los números de punto flotante no pasan suavemente a cero; no hay un número “infinitesimalmente pequeño pero distinto de cero” representable en una computadora. En su lugar, usamos la definición [eq:1.5] para formar una aproximación a la derivada como\[\tag{eq:1.6} \frac{d y}{d t} \approx \frac{y(t + h) - y(t)}{h}\] donde\(h\) es un número pequeño. A esto se le llama la aproximación de “diferencia hacia adelante” de la derivada.

Primeras derivadas de la serie Taylor

Es fácil anotar la aproximación [eq:1.6] recordando la definición de secundaria de un derivado. Sin embargo, obtenemos cierta apreciación por la precisión de aproximar derivados derivándolos usando expansiones de la serie Taylor. Supongamos que conocemos el valor de una función\(y\) en su momento\(t\) y queremos saber su valor en un momento posterior\(t+h\). ¿Cómo encontrar\(y(t+h)\)? La expansión de la serie de Taylor dice que podemos encontrar el valor en un momento posterior por\[\tag{eq:1.7} y(t+h) = y(t) + h \frac{d y}{d t} \biggr\rvert_{t} + \frac{h^2}{2} \frac{d^2 y}{d t^2} \biggr\rvert_{t} + \frac{h^3}{6} \frac{d^3 y}{d t^3} \biggr\rvert_{t} + O(h^4)\] La notación\(O(h^4)\) significa que hay términos de poder\(h^4\) y arriba en la suma, pero los consideraremos detalles que podemos ignorar.

Podemos reorganizar [eq:1.7] para poner la primera derivada en el LHS, cediendo\[\nonumber \frac{d y}{d t} \biggr\rvert_{t} = \frac{y(t+h) - y(t)}{h} - \frac{h}{2} \frac{d^2 y}{d t^2} \biggr\rvert_{t} - \frac{h^2}{6} \frac{d^3 y}{d t^3} \biggr\rvert_{t} - O(h^4)\] Ahora hacemos la suposición que\(h\) es muy pequeña, así podemos desechar términos de orden\(h\) y arriba de esta expresión. Con esa suposición obtenemos\[\nonumber y(t+h) \approx y(t) + h \frac{d y}{d t} \biggr\rvert_{t}\] cuál se puede reorganizar para dar,\[\tag{eq:1.8} \frac{d y}{d t} \approx \frac{y(t + h) - y(t)}{h}\] es decir, la misma expresión de diferencia hacia adelante que se encontró en [eq:1.6] anteriormente. No obstante, tenga en cuenta que para obtener esta aproximación tiramos a la basura todos los términos de orden\(h\) y superiores. ¡Esto implica que cuando usamos esta aproximación incurrimos en un error! Ese error estará en el orden de\(h\). En el límite\(h \rightarrow 0\) el error desaparece pero como las computadoras solo pueden usar finito\(h\), siempre habrá un error en nuestros cómputos, y el error es proporcional a\(h\). Expresamos este concepto diciendo las escalas de error como\(O(h)\).

Usando las expansiones de la serie Taylor podemos descubrir otros resultados. Considera sentarte en el momento\(t\) y pedir el valor de\(y\) a tiempo\(t - h\) en el pasado. En este caso, podemos escribir una expresión para el valor pasado de\(y\) como\[\tag{eq:1.9} y(t-h) = y(t) - h \frac{d y}{d t} \biggr\rvert_{t} + \frac{h^2}{2} \frac{d^2 y}{d t^2} \biggr\rvert_{t} - \frac{h^3}{6} \frac{d^3 y}{d t^3} \biggr\rvert_{t} + O(h^4)\] Note los signos negativos en los términos de orden impar. Similar a la expresión de diferencia hacia adelante anterior, es fácil reorganizar esta expresión y luego desechar términos de\(O(h)\) y arriba para obtener una aproximación diferente para la derivada,\[\tag{eq:1.10} \frac{d y}{d t} \approx \frac{y(t) - y(t-h)}{h}\] Esto se llama la aproximación de “diferencia hacia atrás” a la derivada. Ya que tiramos términos de\(O(h)\) y superiores, esta expresión para la derivada también conlleva una penalización por error de\(O(h)\).

Ahora considere formar diferencia entre las series Taylor [eq:1.7] y [eq:1.9]. Cuando restamos uno del otro obtenemos\[\tag{eq:TaylorsExpansionDifference} \nonumber y(t+h) - y(t-h) = 2 h \frac{d y}{d t} \biggr\rvert_{t} + 2 \frac{h^3}{6} \frac{d^3 y}{d t^3} \biggr\rvert_{t} + O(h^5)\] Esta expresión puede ser rearreglada para convertirse\[\nonumber \frac{d y}{d t} \biggr\rvert_{t} = \frac{y(t+h) - y(t-h)}{2 h} - \frac{h^2}{6} \frac{d^3 y}{d t^3} \biggr\rvert_{t} + O(h^4)\] Ahora si tiramos a la basura términos de\(O(h^2)\) y por encima, obtenemos la llamada aproximación de “diferencia central” para la derivada,\[\tag{eq:1.11} \frac{d y}{d t} \biggr\rvert_{t} \approx \frac{y(t+h) - y(t-h)}{2 h}\] Tenga en cuenta que para obtener esta expresión descartamos \(O(h^2)\)términos. Esto implica que el error incurrido al usar esta expresión para una derivada es\(O(h^2)\). Como generalmente tenemos\(h \ll 1\), el error de diferencia central\(O(h^2)\) es menor que el\(O(h)\) incurrido cuando se usan las fórmulas de diferencia hacia adelante o hacia atrás. Es decir, la expresión de diferencia central [eq:1.11] proporciona una aproximación más precisa a la derivada que las fórmulas de diferencia hacia adelante o hacia atrás, y debería ser su aproximación derivada preferida cuando pueda usarla.

En cada una de estas derivaciones tiramos términos de algún orden\(p\) (y superiores). Descartar términos de pedido\(p\) y anteriores significa que ya no tenemos una serie completa de Taylor. Esta operación se llama “truncamiento”, es decir, hemos truncado (picado) los términos restantes de la serie completa de Taylor. El error incurrido por esta operación se denomina, por lo tanto, “error de truncamiento”.

Segundos derivados de la serie Taylor

También podemos obtener una aproximación para la segunda derivada a partir de las expresiones [eq:1.7] y [eq:1.9]. Esta vez, formar la suma de las dos expresiones para obtener\[\nonumber \label{eq:TaylorsExpansionSum} y(t+h) + y(t-h) = 2 y(t) + 2 \frac{h^2}{2} \frac{d^2 y}{d t^2} \biggr\rvert_{t} +O(h^4)\] Esto puede ser reordenado para obtener una expresión para la segunda derivada,\[\nonumber \frac{d^2 y}{d t^2} \biggr\rvert_{t} = \frac{y(t+h) -2 y(t) + y(t-h)} {h^2} -O(h^2)\] Si bajamos el\(O(h^2)\) término, obtenemos la aproximación a la segunda derivada,\[\tag{eq:1.12} \frac{d^2 y}{d t^2} \biggr\rvert_{t} \approx \frac{y(t+h) -2 y(t) + y(t-h)} {h^2}\] Y ya que bajamos el\(O(h^2)\) término a hacer esta aproximación, significa que el uso de [eq:1.12] incurrirá en un error de\(O(h^2)\) al usar esta aproximación.

Resumen del capítulo

Estos son los puntos importantes que se hacen en este capítulo:

• Resolver una ODE numéricamente necesita dos datos: La ODE y una condición inicial. Tales problemas se denominan “problemas de valor inicial”, o IVP.
• Como matemáticos, estamos acostumbrados a funciones\(y(t)\) que aceptan cualquier valor continuo\(t\) y emiten un valor. Sin embargo, cuando se trata de computadoras, con frecuencia debemos usar “funciones muestreadas” en las que el continuo\(y(t)\) se reemplaza por muestras\(y_n\) tomadas en puntos regulares y discretos en el tiempo,\(t_n\). Los solucionadores de ODE presentados en este folleto entran dentro de esta categoría: proporcionan muestras de la solución en momentos discretos, similares a instantáneas de la función continua que intentan aproximar.
• resume las cuatro aproximaciones diferentes para los derivados que hemos encontrado hasta el momento. Hay muchas más aproximaciones derivadas de orden superior, y usando más términos. Las aproximaciones de orden superior dan mejor precisión a costa de complejidad adicional. Las aproximaciones de orden superior se utilizan con menos frecuencia que las cuatro que se muestran aquí.

Derivados de diferencia finita de uso común.

Derivada	Nombre del método	Expresión	Orden de error
\(\frac{d y}{d t}\)	Diferencia hacia adelante	\(\frac{y_{n+1}-y_n}{h}\)	\(h\)
\(\frac{d y}{d t}\)	Diferencia hacia atrás	\(\frac{y_{n}-y_{n-1}}{h}\)	\(h\)
\(\frac{d y}{d t}\)	Diferencia central	\(\frac{y_{n+1}-y_{n-1}}{2 h}\)	\(h^2\)
\(\frac{d^2 y}{d t^2}\)	Segunda derivada	\(\frac{y_{n+1}-2 y_{n}+y_{n-1}}{h^2}\)	\(h^2\)