1.2: Método Euler hacia delante

Algoritmo Euler

Ahora examinamos nuestro primer solucionador de ODE: el método Forward Euler. Aquí está el problema y el objetivo: Dada una ODE escalar, de primer orden,\[\tag{eq:2.1} \frac{d y}{d t} = f(t, y)\] y una condición inicial\(y(t=0) = y_0\), encontrar cómo\(y(t)\) evoluciona la función para todos los tiempos\(t > 0\). En particular, anotar un algoritmo que puede ser ejecutado por una computadora para encontrar la evolución de\(y(t)\) para todos los tiempos.

Para derivar el algoritmo, primero reemplace la ecuación exacta con una aproximación basada en la derivada de diferencia hacia adelante para obtener\[\tag{eq:2.2} \frac{y(t + h) - y(t)}{h} \approx f(t, y)\] Ahora discretizar la ecuación. Eso significa que reemplazamos nuestra función\(y(t)\) definida en continuo\(t\) con una función muestreada\(y_n\) definida en tiempos discretos\(t_n\). Es decir,\(y_n = y(t_n)\). También imaginamos que el paso de tiempo entre muestras es pequeño,\(h = t_{n+1} - t_n\). En este caso, [eq:2.2] se convierte en\[\tag{eq:2.3} \frac{y_{n+1} - y_n}{h} \approx f(t_n, y_n)\] Avanzando, reemplazaremos el\(\approx\) letrero\(=\) por conveniencia, y tendremos en cuenta que detrás de nuestra expresión se esconde un error de aproximación que crece con el aumento\(h\). A continuación, imagínese que estamos sentados en el momento presente\(t_n\), y reescribir [eq:2.3] para trasladar el futuro al LHS y el presente al RHS. Obtenemos\[\tag{eq:2.4} y_{n+1} = y_n + h f(t_n, y_n)\] Ahora observa: Esta expresión dice que si conocemos los valores de\(t_n\) y\(y_n\) en el presente, entonces para obtener el valor futuro solo\(y_{n+1}\) realizamos el cómputo en el RHS. Es decir, la ecuación [eq:2.4] describe una manera de dar un paso adelante en el tiempo. Comenzamos en el momento\(t=0\) con la condición inicial\(y = y_0\) y usamos la ecuación [eq:2.4] para dar un paso a\(y_1\), luego usamos ese resultado para dar un paso a\(y_2\), y luego\(y_3\), y así sucesivamente. Al iterar [eq:2.4] generamos un vector de\(y_n\) valores que constituyen la versión muestreada de la función\(y(t)\).

El algoritmo 1 muestra pseudocódigo implementando el método de Euler hacia adelante. Una representación gráfica

__________________________________________________________________________________________________________________________________________________

Método Euler hacia adelante del algoritmo 1

__________________________________________________________________________________________________________________________________________________

Entradas: condición inicial\(y_0\), tiempo de finalización\(t_{end}\).

Inicializar:\(t_0 = 0, y_0\).

para\(n = 0: t_{end}/h\) hacer

\(t_n = n h\)

\(y_{n+1} \leftarrow y_n + h f(t_n, y_n)\)

fin para

\(y\)vector de retorno.

__________________________________________________________________________________________________________________________________________________

del algoritmo se muestra en 2.1. Aquí hay algunas cosas para notar sobre el delantero Euler:

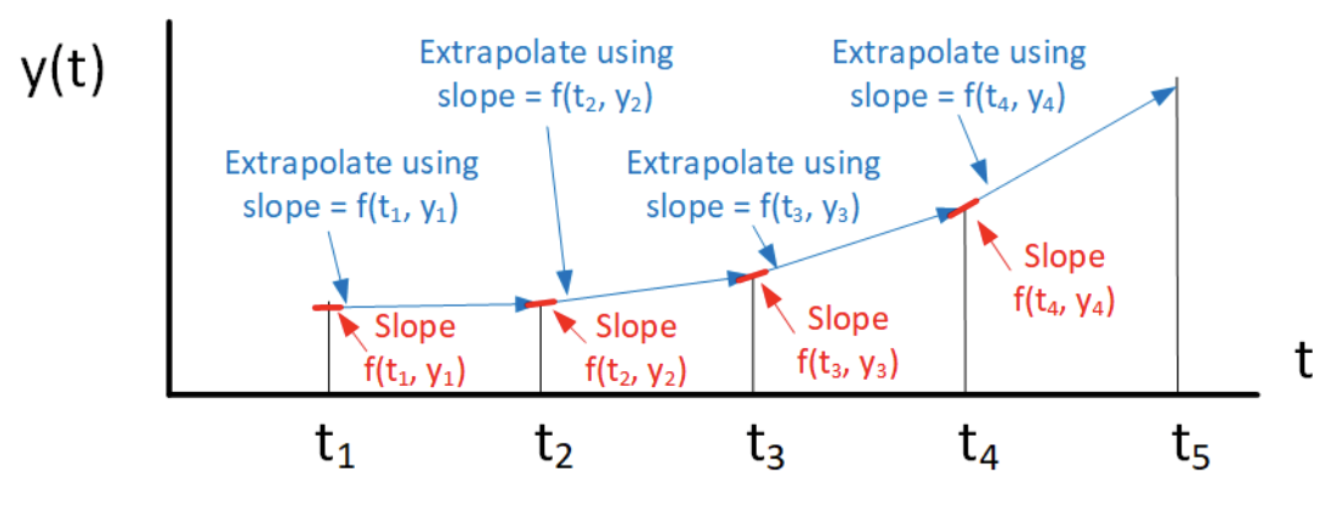
Figura 2.1: El algoritmo de Euler hacia adelante. En cada paso de tiempo el algoritmo calcula la pendiente de\(f(t, y)\), luego avanza por paso\(h\) para encontrar el siguiente valor de\(y\). La pendiente a utilizar es la pendiente de la curva al inicio del intervalo. Esta figura muestra un problema con este algoritmo: la solución real puede curvarse alejándose de la solución calculada ya que Euler hacia adelante usa la pendiente antigua en\(t_n\) para calcular el paso, y esa pendiente puede no apuntar el método a la correcta\(y_{n+1}\) en el momento\(t_{n+1}\).

Aquí hay algunas cosas para notar sobre el delantero Euler:

• Haciendo referencia a 2.1, puede ver que calculamos la solución se basa en calcular la pendiente de\(y\) usar\(f(t,y)\) (es decir, la derivada) en cada punto\(t_n\), luego usar la pendiente para extrapolar\(y\) hacia adelante un paso. En la figura la gruesa línea azul denota la pendiente en cada una\(t_n\). Tenga en cuenta que la pendiente utilizada es la pendiente al inicio del intervalo de escalón, de ahí el nombre “adelante” Euler. Se puede ver como cada paso adelante está determinado por la pendiente de la línea azul.
• Adelante Euler es una instancia de un llamado “método explícito”. Explícito significa que todos los cálculos requeridos para dar el paso están presentes en el RHS de [eq:2.4].
• muestra claramente un problema con el delantero Euler: La solución real puede desviarse de la solución de Euler hacia adelante, provocando que se acumule un error en la solución de Euler hacia adelante. El error depende claramente del tamaño de\(h\): Más grande\(h\) conducirá a un error mayor, mientras que el menor\(h\) conduce a un error más pequeño. La dificultad con los más pequeños\(h\) es que los tamaños de paso más pequeños requerirán más pasos —y un tiempo de cálculo más largo— para alcanzar el mismo tiempo de finalización,\(t_{end}\).

Además de entender las matemáticas detrás del método, hay importantes características de implementación para notar. El código que implementa adelante Euler se divide en tres partes:

1. Un programa principal de nivel superior llamado “test forward euler”. Este es el programa que ejecuta el usuario. Establece los parámetros del modelo utilizados e invoca al propio solucionador. Luego realiza parcelas del resultado.
2. La implementación del solucionador llamó “forward euler”. Esta función está escrita de manera genérica, por lo que no establece ningún detalle ni de los parámetros de la ODE en particular bajo consideración, ni características del algoritmo como el tamaño del paso. El objetivo es tener un solucionador genérico que pueda ser utilizado en cualquier ODE sin modificación.
3. Una implementación de las ecuaciones ODE contenidas en un archivo llamado “f”. Esto corresponde a la función\(f(t_n, y_n)\) en [eq:2.4]. Los parámetros del modelo se pasan directamente del nivel superior a “f” como variables globales.

Un diagrama de bloques que muestra esta arquitectura se presenta en 2.2.

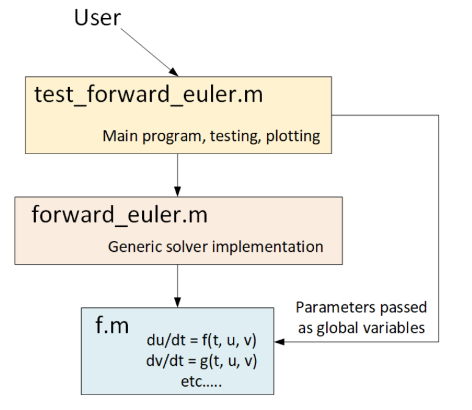
Figura 2.2: La arquitectura de tres capas utilizada en el ejemplo de programas de Matlab implementando hacia adelante Euler. El usuario ejecuta el programa principal llamado “test forward euler”. Esto a su vez llama al solucionador “forward euler”, que a su vez llama a la función “f” que contiene la ODE real. Un patrón de diseño similar se utiliza para casi todos los solucionadores presentados en este folleto.

La arquitectura en 2.2 es un simple “patrón de software”, lo que significa que es una buena manera de dividir el código en diferentes piezas, cada una de las cuales realiza una función específica. Casi todos los ejemplos de solucionadores de ODE que presento en este folleto están arquitectónicos utilizando este patrón de tres capas. Los solucionadores de ODE del mundo real como Sundials o diferencialecuations.JL también se particionan frecuentemente en diferentes piezas, aunque sus arquitecturas son generalmente más complicadas y tienen más piezas. Las piezas adicionales podrían manejar, por ejemplo, inicialización del solucionador, administración de memoria, manejo de errores, análisis de sensibilidad, etc. El punto es que es útil particionar su programa en diferentes piezas que manejan funciones lógicamente distintas. En efecto, esta es una de las cosas más importantes que aprendes a hacer al convertirte en ingeniero de software.

Ejemplo: la ODE de crecimiento exponencial

Como primer ejemplo de nuestro solucionador simple, aplicaremos adelante Euler para integrar la ODE de crecimiento exponencial, ya\[\tag{eq:2.5} \frac{d y}{d t} = \alpha y\] conocemos la solución a esta ecuación —lo es\(y(t) = y(0) e^{\alpha t}\). Para\(\alpha < 0\) la solución decae a cero para\(t \rightarrow \infty\), mientras que para\(\alpha > 0\) la solución escapa al infinito para\(t \rightarrow \infty\).

Ahora usa la prescripción para discretizar la ecuación para adelante Euler y obtener\[\tag{eq:2.6} y_{n_+1} = y_n + h\alpha y_n\] El resultado calculado usando forward Euler se muestra en 2.3 para valores variables de\(\alpha\).

Figura 2.3: La solución a [eq:2.5] computada usando el algoritmo de Euler hacia adelante para diferentes valores de\(\alpha\). La función calculada\(y_n\) se grafica usando círculos abiertos y la solución analítica se grafica usando líneas rojas. El tamaño de paso utilizado fue\(h=0.1\). Tenga en cuenta que las soluciones calculadas y analíticas no coinciden exactamente, particularmente el caso donde\(\alpha = 0.3\).

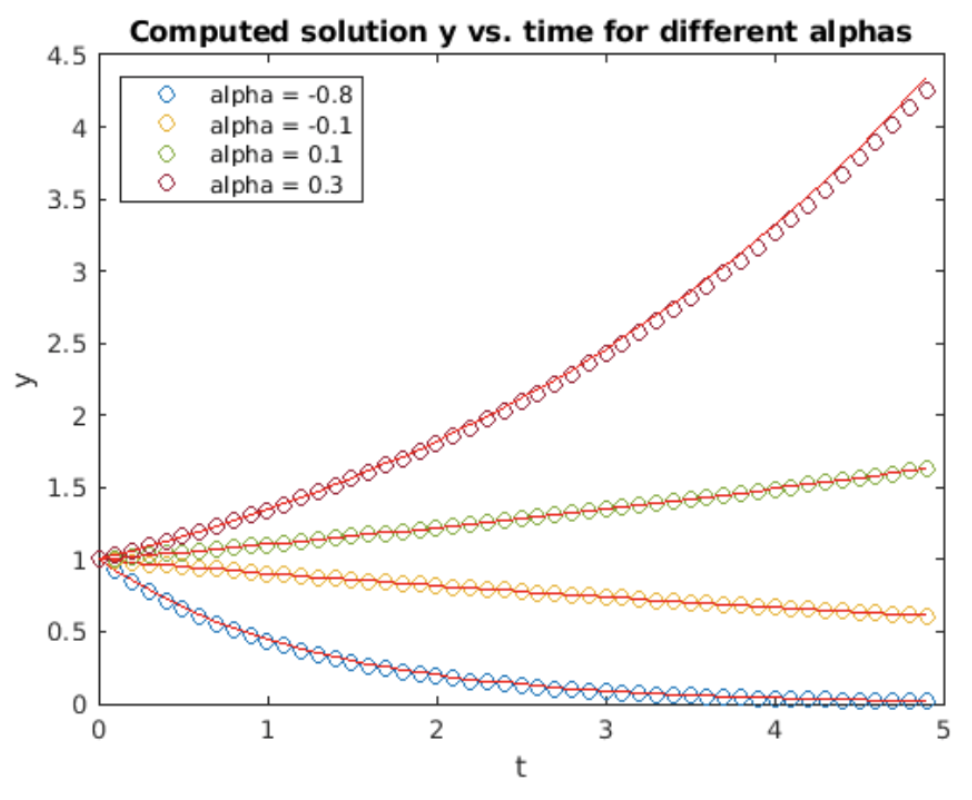
La figura muestra que la solución calculada no rastrea exactamente la solución analítica. ¿Qué está mal? La respuesta tiene que ver con los errores incurridos al utilizar la fórmula de diferencia hacia adelante para aproximar la derivada. Recordemos que la expresión de diferencia hacia adelante [eq:1.8] sólo es verdadera en el límite donde el tamaño de paso va a cero,\(h \rightarrow 0\). Para los distintos de cero\(h\), la aproximación de diferencia hacia delante es inexacta, y por la derivación presentada en 1.3.1 la magnitud de las escalas de error como\(O(h)\). Podemos cuantificar esto examinando el error RMS de la solución calculada. El error RMS se calcula comparando la diferencia cuadrática media raíz entre la solución calculada y la analítica de la siguiente manera:\[\tag{eq:2.7} e = \sqrt{\frac{1}{N} \sum_{i=1}^{N} \left( y_t(i) - y_c(i) \right)^2 }\] Aquí,\(y_t\) está la solución “matemáticamente verdadera” (analítica),\(y_c\) es la solución calculada usando Euler hacia adelante, \(N\)es el número de puntos de muestreo en la solución, y\(e\) es el error RMS. Esto también se llama el “error global” en algunos libros de texto. Esperamos que el error RMS aumente con el aumento\(h\): las estepsias más grandes acumulan errores más grandes. La pregunta es, ¿cómo se comporta el error\(h\)? Una gráfica de error RMS vs.\(h\) Se muestra en la fig. 2.4.

En la gráfica log-log el error RMS aumenta con\(h\) siguiendo una línea recta. Una característica útil de las gráficas log-log es que revela claramente las relaciones poder-ley. Específicamente, si una función obedece a una ley de potencia\(y \sim x^p\), entonces la pendiente de la\(x\) línea\(y\) vs. en una gráfica logarítmica es la potencia\(p\). Esto se puede entender tomando el tronco de ambos lados de la ley de potencia (que es lo que hace el trazado en una escala log-log) y señalando que\(p\) se convierte en la pendiente de la línea. La pendiente de la línea en la fig. 2.4 es exactamente

Figura 2.4: El error incurrido por el método de Euler hacia delante frente al tamaño de paso\(h\) trazado en una escala log-log. Tenga en cuenta que la pendiente de los puntos de error es uno. Esto implica el error\(e \sim O(h)\).

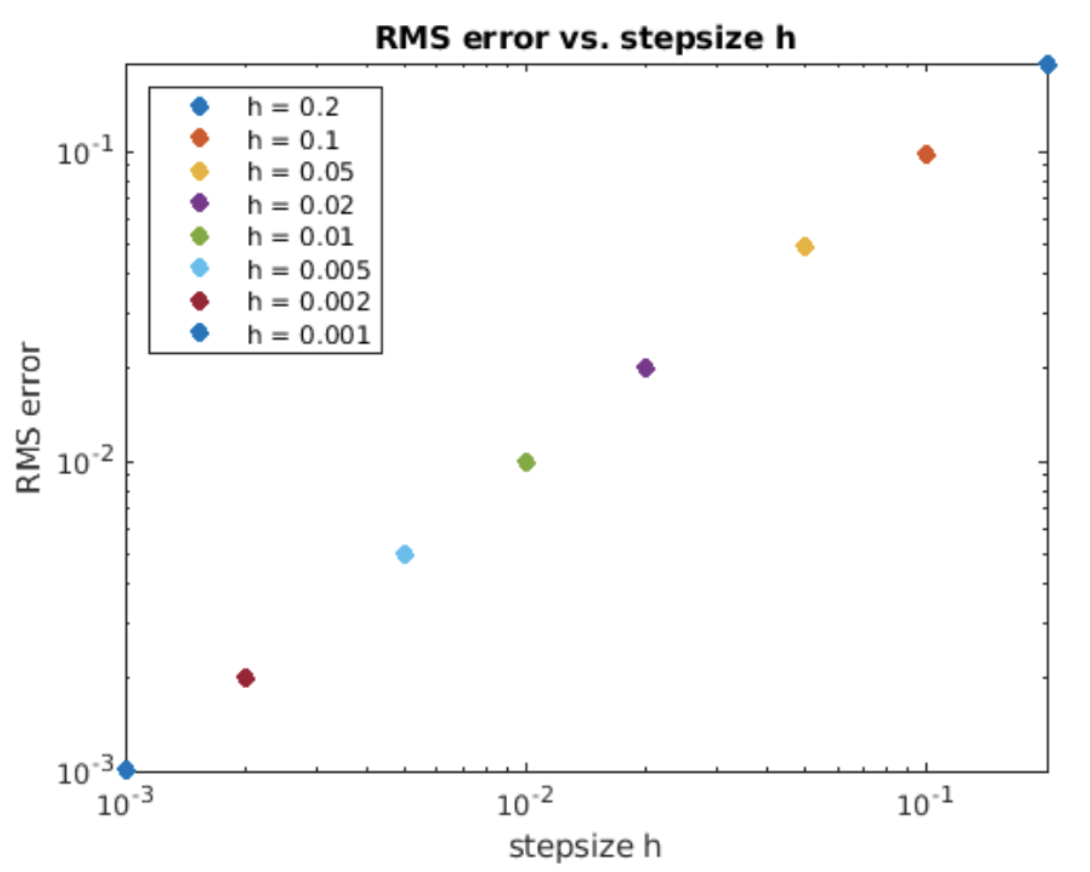
1 — Esto significa que el error RMS incurrido por el método Euler directo es proporcional al tamaño de paso

\(h\)— es decir, error\(e \sim O(h)\). Esta relación de escalado se derivó en 1.3.1 cuando la expresión de diferencia hacia adelante se derivó de la serie Taylor, los términos de\(O(h)\) y anteriores se descartaron para obtener la expresión de diferencia hacia adelante, lo que significa que el uso de la aproximación lleva un\(O(h)\) penalización por error.

Desvío: error de truncamiento local vs. error de solución global

De vuelta en 1.3.1 mostré cómo las aproximaciones a la derivada se derivaron de la serie Taylor. También mencioné que al dejar caer términos de orden superior, aceptábamos implícitamente que nuestras soluciones calculadas solo podían ser aproximaciones a la solución “matemáticamente verdadera”. Es decir, la solución computada llevaba un error, y la principal causa de error se debió al truncamiento de la serie Taylor. Este error a veces se denomina “error de truncamiento local” o “LTE” en la literatura ODE. Generalmente caracterizamos la LTE en términos de escalado de tamaño de paso\(O(h^p)\). Generalmente, el orden de error\(p\) es el mismo que el primer término truncado de la serie Taylor. Es decir, si el primer término truncado es\(h\) entonces el LTE escala como\(O(h)\).

Ahora en la sección anterior introducimos el error RMS [eq:2.7]. Dado que el error RMS es una suma en toda la solución, es un error global: suma contribuciones de todos los errores presentes en toda la solución. (Está normalizado por\(N\), pero no obstante es sensible a todos los errores.) Por lo tanto, este error se denomina a veces el “error global” o GE en la literatura ODA. Nuevamente, el GE se caracteriza por cómo escala con\(h\). Todos los análisis de errores mostrados en este folleto son errores globales calculados usando la fórmula [eq:2.7] y se expresan como gráficas de escala similares a las mostradas en la fig. 2.4.

La LTE y la GE son cantidades conceptualmente distintas. Por lo tanto, podría preguntarse “¿cuál es la relación entre ambos?” Es decir, ¿miden lo mismo? La respuesta es “sí”. Aunque no lo haré aquí, se puede probar que la LTE y la GE obedecen la misma relación de escalado para cualquier método dado. Es decir, si el LTE escala como\(O(h^p)\), entonces el GE también escala como\(O(h^p)\). En consecuencia, aunque hablo vagamente de “el error” sin cuantificar exactamente a lo que me refiero, la equivalencia de la LTE y la GE son suficientes para garantizar que el término “el error” se refiere a algo que puede ser cuantificado, y es una métrica significativa con la que medir los diferentes solucionadores de ODE presentados en este folleto.

Ejemplo: un sistema accionado

Ahora volvamos a resolver ODEs. Una ODE un poco más complicada es esta ODE lineal con un término de conducción. \[\tag{eq:2.8} \frac{d y}{d t} = A \sin(\omega t) - \alpha y\]Dado que la ecuación es lineal, la solución general es la suma de dos piezas: un término homogéneo y un término no homogéneo (a veces llamado la “solución particular”). Consideraremos el caso de positivo\(\alpha\). Es decir, para\(t \rightarrow \infty\) la solución homogénea se desintegrará ya\(e^{-\alpha t}\) que el comportamiento a largo plazo del sistema viene determinado por el término forzoso\(A \sin(\omega t)\). La solución analítica a la ecuación se puede encontrar después de algún álgebra,\[\tag{eq:2.9} y(t) = C e^{-\alpha t} + B \cos(\omega t + \phi)\] Ajustamos las constantes\(B\),\(C\), y\(\phi\) para que coincida con las condiciones iniciales así como asegurar que la solución particular obedezca [eq:2.8] para \(t \rightarrow \infty\). Para realizar la gráfica que se muestra a continuación en la fig. 2.5 elegimos\(y(0) = 1\). Con esta condición inicial, un ejercicio de álgebra fácil mostrará que las constantes de ajuste son\[\begin{aligned} \nonumber \phi &= \arctan \left( \frac{\alpha}{\omega} \right) \\ \nonumber B &= \frac{-A}{\omega \cos(\phi) + \alpha \sin(\phi)} \\ \nonumber C &= 1 - B \cos(\phi)\end{aligned}\]

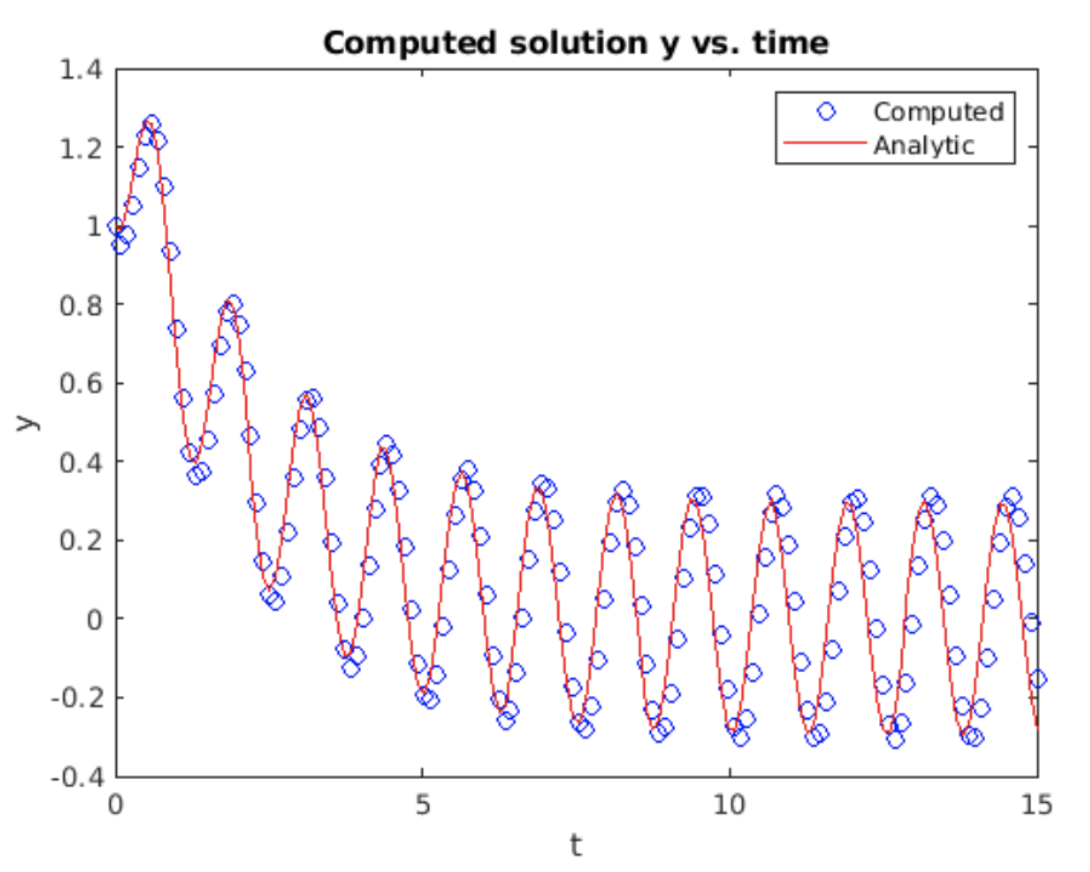
Discretizado para Euler hacia adelante, la iteración se\[\tag{eq:2.10} y_{n_+1} = y_n + h(A \sin(\omega t_n) - \alpha y_n)\] muestra la solución calculada a [eq:2.8] durante 15 segundos asumiendo\(A = 1.5\),\(\omega = 5\) y\(\alpha = 0.5\). La solución muestra claramente un transitorio inicial que decae, dejando una solución que se comporta como una onda sinusoidal como\(t \rightarrow \infty\).

Figura 2.5: La solución para [EQ:ForwardeulerDriven] calculada usando el algoritmo de Euler hacia adelante. La función calculada\(y_n\) es trazada por los círculos azules y la solución analítica se traza usando líneas rojas. Aunque las dos soluciones están cerca, no coinciden exactamente, y la solución avanzada de Euler parece divergir de la solución analítica con el aumento\(t\).

Ejemplo: la ecuación logística

Aquí hay un ejemplo de una ODE no lineal: la ecuación logística. Esta ODE puede considerarse como un modelo muy sencillo de dinámica poblacional. Aquí está la ODE:\[\tag{eq:2.11} \frac{d y}{d t} = \left( 1 - \frac{y}{Y_m} \right) y\] Si piensas en\(y\) como la población de algunas especies animales, cuándo\(y \ll Y_m\), entonces la población puede crecer exponencialmente. Pero a medida que la población\(y \rightarrow Y_m\), la tasa de crecimiento de la población se satura. Piense en conejos que viven en un campo de zanahorias —cuando hay muy pocos conejos (y no hay preditores) entonces los conejos tienen muchas zanahorias para comer y pueden reproducirse libremente, lo que lleva a un crecimiento exponencial. No obstante, si en el campo viven demasiados conejos, entonces comen la mayoría de las zanahorias y ya no pueden reproducirse libremente ya que la comida es escasa. En consecuencia, la población de conejos tiende hacia un límite fijo dado por\(y = Y_m\).

Esta ecuación tiene la siguiente solución analítica:\[\tag{eq:2.12} y(t) = \frac{y_0 e^t}{ \left( 1 + \frac{y_0}{Y_m} e^t \right) }\] donde\(y_0\) se utiliza para hacer coincidir la condición inicial. Muestra de inspección\(y_0 = y(t=0)\). También tenga en cuenta que cuando\(y = Y_m\) la tasa de crecimiento (derivado) va a cero, consistente con la intuición de que la población de conejos debe saturarse cuando los conejos comen la mayor parte de las zanahorias. Sólo quedan suficientes zanahorias para llevar a la población de conejos, pero la población ya no puede crecer.

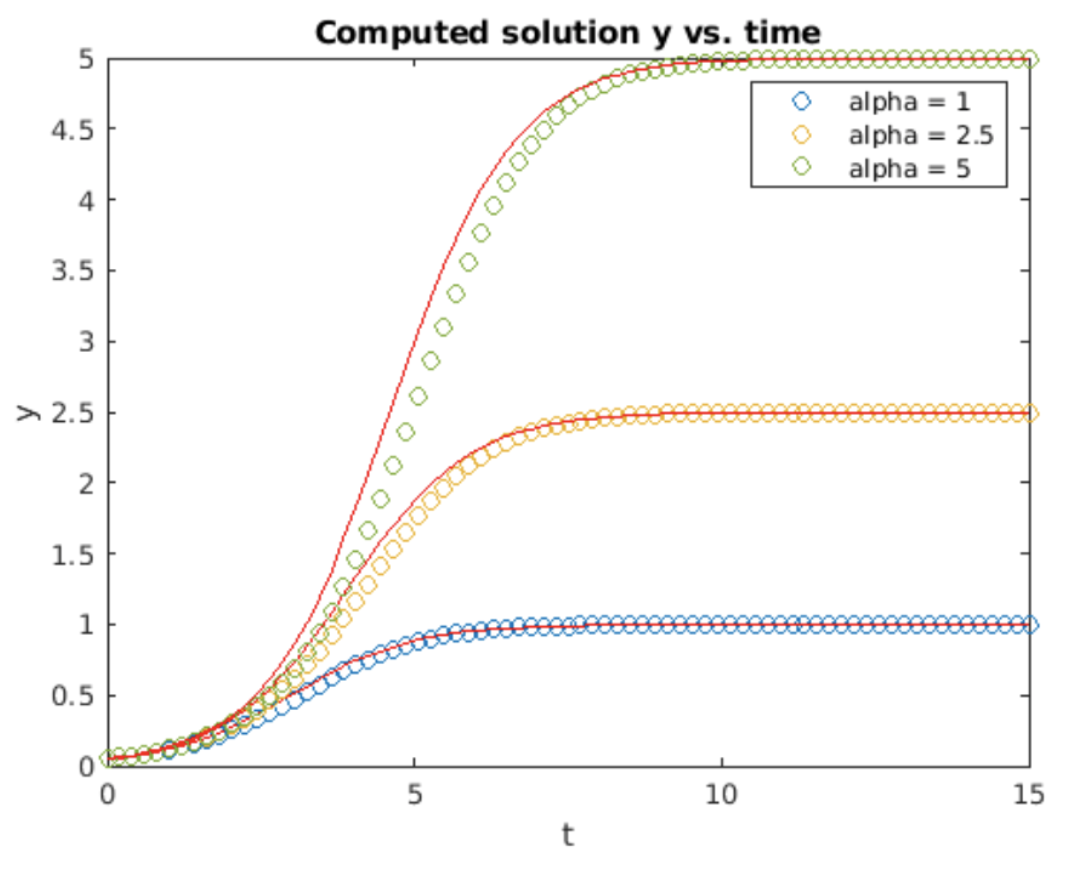
Discretizado para Euler hacia adelante, la iteración a implementar para la ecuación logística es\[\tag{eq:2.13} y_{n_+1} = y_n + h \left( 1 - \frac{y_n}{Y_m} \right) y_n\] Esta iteración se implementó en Matlab y luego se ejecutó para tres valores diferentes de\(Y_m\). Los resultados se muestran en la fig. 2.6. Euler delantero reproduce bastante bien el comportamiento de saturación de la ecuación logística, después de que alrededor de\(t = 10\) la solución de Euler hacia adelante coincide con la solución analítica. Sin embargo, el delantero Euler hace un peor trabajo reproduciendo el periodo de crecimiento exponencial alrededor\(t = 5\): el delantero Euler se queda atrás en la solución analítica. Este comportamiento es similar al observado en la ODE de crecimiento exponencial mostrada en la fig. 2.3.

Figura 2.6: La solución a [EQ:ForwardeulerLogistic] computada usando el algoritmo de Euler hacia adelante para tres\(Y_m\) valores diferentes. La función calculada\(y_n\) se grafica usando círculos abiertos y la solución analítica se grafica usando líneas rojas. Tenga en cuenta que la solución calculada se queda atrás (está por detrás) de la solución analítica; la solución de Euler hacia adelante conlleva un error. Se puede imaginar la población de conejos partiendo de una base baja y creciendo hasta llegar a un punto de saturación. El punto de saturación está determinado por el valor de\(Y_m\).

Extendiendo hacia adelante Euler a orden superior

Hasta el momento, hemos tratado con ODEs escalares de primer orden como la que se muestra en la Ecuación [eq:2.1]. Muchas ODE que se encuentran en la práctica son de orden superior. Por ejemplo, consideremos la ODE de segundo orden más famosa de todas: la segunda ley de Newton:\(F = ma\). Dice que imponer una fuerza a un cuerpo provocará que se acelere en la dirección de la fuerza aplicada. Dado que la aceleración es la segunda derivada de la posición del cuerpo\(a = d^2 y/ d t^2\), esto implica que podemos escribir la segunda ley de Newton como una ODE:\[\tag{eq:2.14} \frac{d^2 y}{d t^2} = F(t, y', y)\] Dada la importancia de la ley de Newton, queremos poder resolver ODEs como [eq:2.14] numéricamente. ¿Cómo extender el método de Euler hacia adelante a ODEs de segundo (y superior) orden?

La manera de resolver [eq:2.14] numéricamente es reorganizarlo para que se convierta en dos ODEs de primer orden de la siguiente manera:

1. Definir dos variables,\(y_1 = dy/dt\) y\(y_2 = y\).
2. Ahora tenga en cuenta que [eq:2.14] puede escribirse como\[\nonumber \frac{d y_1}{d t} = \frac{d^2 y}{d t^2} = F(t, y', y)\]
3. A continuación, por definición tenemos\[\nonumber \frac{d y_2}{d t} = \frac{d y}{d t} = y_1\]
4. Por lo tanto, hemos dividido [eq:2.14] en dos ODE acopladas de primer orden,\[\begin{aligned} \nonumber \frac{d y_1}{d t} &= F(t, y_1, y_2) \\ \nonumber \frac{d y_2}{d t} &= y_1 \end{aligned}\]
5. Este sistema de dos ODEs de primer orden puede resolverse usando Euler hacia adelante utilizando los mismos métodos que en 2.1.

Esta técnica de romper una ODE de segundo orden en dos ODEs de primer orden puede generalizarse fácilmente. Como regla general, si comienzas con una ODA de orden\(n\) th, puedes descomponerla en ODEs de\(n\) primer orden. Entonces el sistema de ODEs de primer orden puede resolverse utilizando hacia adelante Euler o cualquiera de los métodos más avanzados que encontraremos más adelante.

No basta con especificar simplemente las ecuaciones a resolver. También necesitamos especificar condiciones iniciales (CI) para este sistema, un IC para cada ecuación. En general, una ODE de orden\(n\) th irá acompañada de condiciones\(n\) iniciales, generalmente una para la función\(y(t=0)\), una para la primera derivada\(y'(t=0)\), una para la segunda derivada\(y''(t=0)\), y así sucesivamente. Por lo tanto, una ODE de segundo orden como [eq:2.14] requerirá dos CI. Usando las definiciones de\(y_1\) y\(y_2\) anteriores, es fácil mapear los CI para la ecuación de segundo orden en los CI para el sistema como\[\begin{aligned} \nonumber y_1(0) &= y'(0) \\ \nonumber y_2(0) &= y(0)\end{aligned}\]

Ejemplo: el oscilador armónico simple

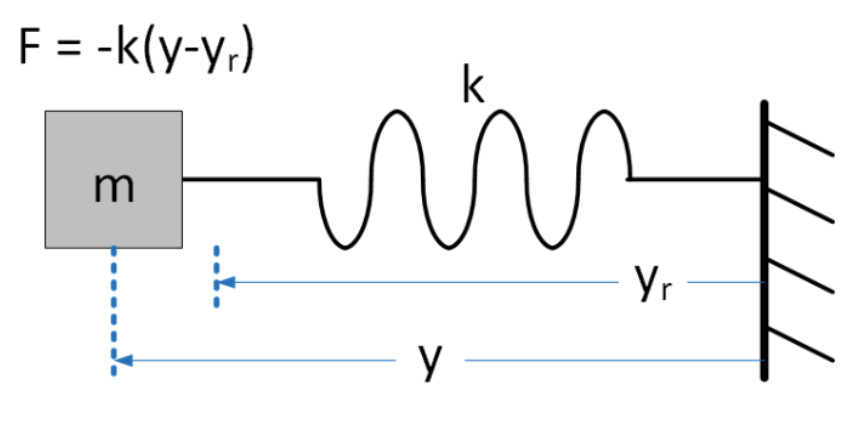
Para concretar estas ideas examinaremos el llamado oscilador armónico simple (SHO). Este es un modelo simple de movimiento oscilatorio amado por los físicos, y encontrado en muchas aplicaciones del mundo real. Una situación modelada por el SHO es una masa que se desliza sobre un piso (sin fricción) y atada a una pared por un resorte. Ver fig. 2.7. La fuerza que impresiona el resorte sobre la masa se modela usando la ley de Hooke, que dice que el resorte intenta restaurar la masa a una posición de equilibrio con una fuerza que varía linealmente con la posición. Tomando\(y\) como posición de la masa, dice la ley de Hooke\(F = -k (y-y_r)\), donde\(k\) es una constante que mide la rigidez del resorte, y\(y_r\) es la posición de reposo de la masa. A partir de ahora nos pondremos\(y_r = 0\) ya que es una constante y no afecta a las matemáticas que queremos explorar.

Combinando la ley de Hooke y la segunda ley de Newton, podemos escribir una ODE de segundo orden describiendo el movimiento de la masa bajo la influencia de la primavera,\[\tag{eq:2.15} \frac{d^2 y}{d t^2} = -\frac{k}{m} y\] Probablemente ya conozcas la (s) solución (s) a esta ecuación. Son senos y cosenos,\[\tag{eq:2.16} y(t) = A \cos(\omega t) + B \sin(\omega t)\]

Figura 2.7: El oscilador armónico simple (SHO). La masa\(m\) se desliza sin fricción en el piso. Se fija a una pared a través de un resorte. La constante de resorte (medida de la rigidez del resorte) es\(k\). Cuando la masa se desplaza de su posición de reposo,\(y_r\) el resorte tiende a empujar o tirar de la masa hacia la posición de reposo. No obstante, la masa rebasa la posición de descanso debido a la segunda ley de Newton. Por lo tanto, el resorte ejecutará una oscilación sinusoidal alrededor\(y_r\), y si el sistema no tiene pérdidas, la oscilación nunca se detendrá. El movimiento oscilatorio se rige por [EQ:Sho], que se conoce como la ecuación del oscilador armónico simple.

donde hemos definido\(\omega = \sqrt{k/m}\) por conveniencia. \(\omega\)generalmente se conoce como la frecuencia de oscilación. Los coeficientes\(A\) y\(B\) están determinados por las condiciones iniciales.

¿Cómo resolver [eq:2.15] numéricamente? Usaremos nuestra receta de la sección 2.6 y dividiremos [eq:2.15] en dos ODE de primer orden. Definimos\(u = dy/dt\) y\(v = y\). (Yo uso\(u\) y\(v\) en lugar de\(y_1\) y\(y_2\) por conveniencia notacional en lo que viene después.) Ahora podemos descomponer [eq:2.15] en\[\tag{2.17} \begin{aligned} \frac{d u}{d t} &= -\frac{k}{m} v \\ \frac{d v}{d t} &= u \end{aligned}\] Ahora discretizar usando la aproximación de diferencia hacia delante a la primera derivada:\[\begin{aligned} \nonumber \frac{u_{n+1} - u_{n}}{h} &= -\frac{k}{m} v_n \\ \nonumber \frac{v_{n+1} - v_{n}}{h} &= u_n\end{aligned}\] Siguiente reorganizar estas ecuaciones para colocar el futuro en el LHS y el presente en el RHS:\[\begin{aligned} u_{n+1} &= u_n -h \frac{k}{m} v_n \\ v_{n+1} &= v_n + h u_n \end{aligned} \tag{eq:2.18}\] Ahora tenemos un par de ecuaciones que podemos pisar ¡adelante en el tiempo! Comenzamos con condiciones iniciales conocidas\(u_0\)\(v_0\) y usamos el sistema para calcular los siguientes valores en el tiempo\(u_1\) y\(v_1\), luego los usamos para obtener los siguientes valores, y así sucesivamente.

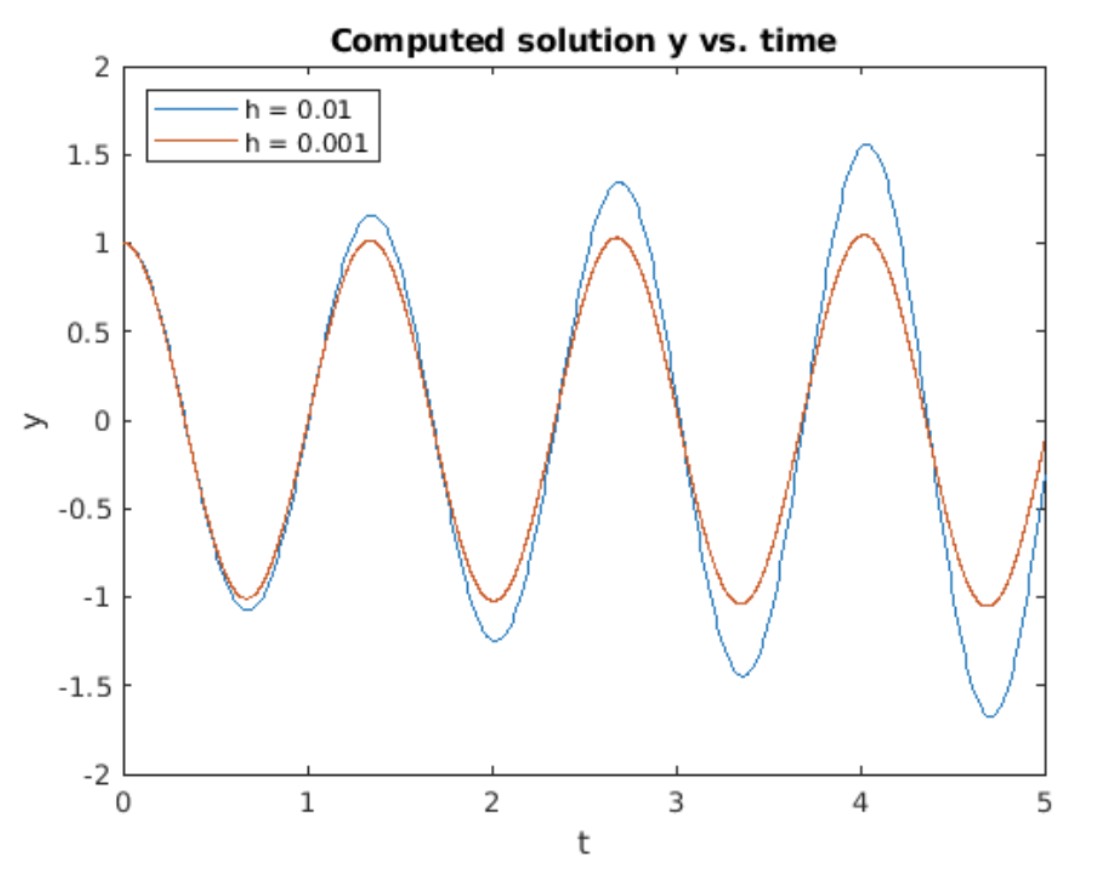
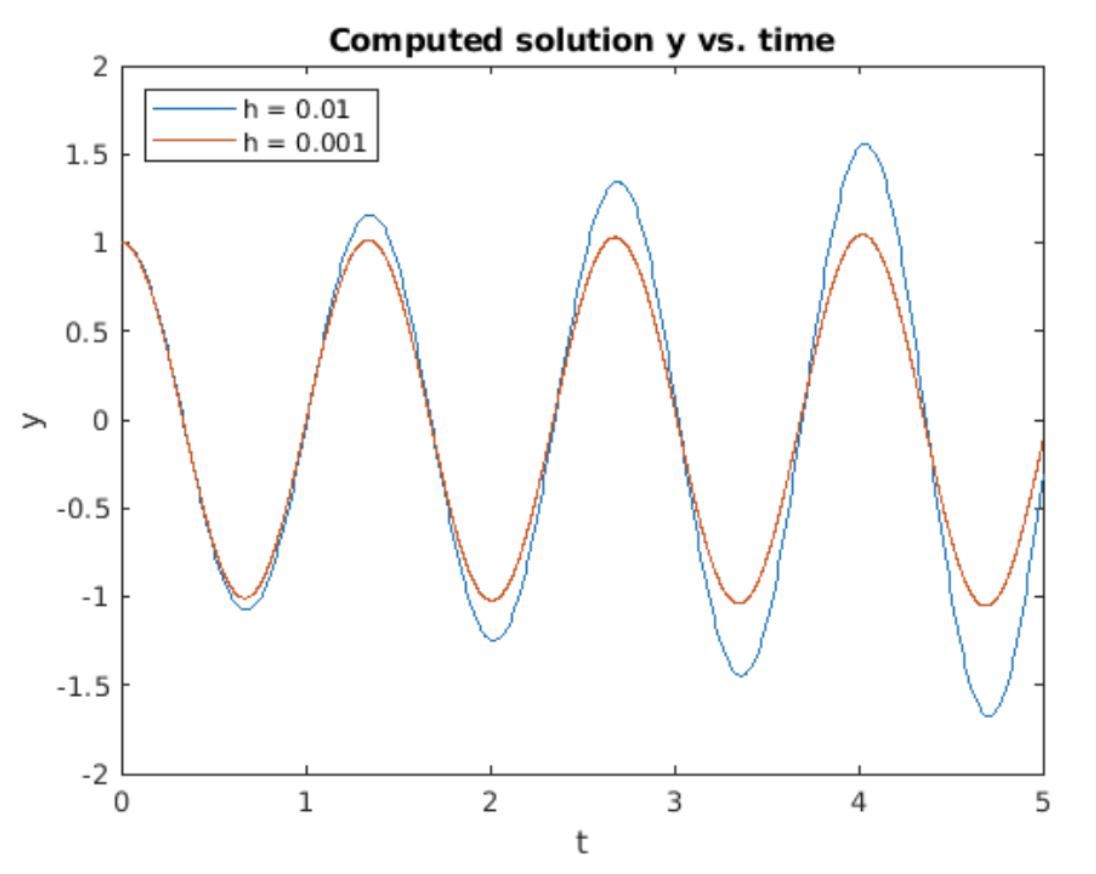
Este algoritmo es fácil de implementar usando, por ejemplo, Matlab. Los resultados de ejecutar un programa Matlab implementando la iteración [eq:2.18] se muestran en la fig. 2.8. Los resultados para dos tamaños de paso diferentes (\(h = 0.01\)y\(h = .001\)) se muestran para la comparación. Las condiciones iniciales\(u_0 = 1\) y\(v_0 = 0\) se utilizaron en ambos casos. Estos CI corresponden a una masa oscilante cuya posición inicial es 1 y cuya velocidad inicial es 0 —similar a tirar de la masa a mano hasta la posición 1, sujetándola ahí por un momento, luego soltándola.

Figura 2.8: El oscilador armónico simple (SHO) resuelto usando Euler directo. Tenga en cuenta que la amplitud sinusoidal aumenta exponencialmente con el tiempo. Esto es contrario a la solución conocida que involucra pecados puros y cosenos. ¿Por qué sucede esto? Este efecto tiene que ver con el concepto de estabilidad discutido más adelante en 2.9.

Cosas a tener en cuenta en la figura:

• Ambas gráficas muestran que la masa oscila de un lado a otro en el tiempo. Esto es de esperar, ya que las soluciones a [eq:2.15] son senos y cosenos.
• No obstante, vemos que ambas soluciones crecen en el tiempo. La\(h = 0.01\) solución crece más rápido que la\(h = .001\) indicada, pero una inspección minuciosa de la parcela muestra que ambas crecen. Esto es inesperado, y es incorrecto —la ODE [eq:2.15] tiene soluciones de pecado y cos que no crecen. ¿Qué está mal? La respuesta a esta pregunta implica estudiar la estabilidad del método forward Euler.

Matriz propagadora para SHO

Antes de hablar de estabilidad, es conveniente refundir la iteración [eq:2.18] en un formato diferente. Debido a que [eq:2.15] es lineal, podemos llevar el sistema Euler un paso más allá. Tenga en cuenta que lo siguiente no funciona con todas las ODEs, ¡solo con ODEs lineales! Con un poco de reordenamiento podemos escribir [eq:2.18] como un sistema matriz-vector,\[\begin{aligned} \begin{pmatrix} u_{n+1} \\ v_{n+1} \end{pmatrix} = \begin{pmatrix} 1 & - h k / m \\ h & 1 \end{pmatrix} \begin{pmatrix} u_{n} \\ v_{n} \end{pmatrix}\end{aligned} \tag{eq:2.19}\] o bien, escrito en forma matriz-vector,\[\label{eq:SHOMatVecForm} \nonumber {y_{n+1}} = {A} {y_n}\] donde\[\nonumber {y_n} = \begin{pmatrix} u_{n} \\ v_{n} \end{pmatrix}\] y\({A}\) es la matriz que se muestra en [eq:2.19]. \({A}\)comúnmente se llama la “matriz propagadora” ya que la multiplicación repetida por\({A}\) propaga (pasos) la solución\({y_n}\) hacia adelante en el tiempo.

El pseudocódigo que implementa el algoritmo de Euler hacia adelante para resolver el oscilador armónico simple se muestra en [alg:2].

__________________________________________________________________________________________________________________________________________________

Algoritmo 2 Método Euler hacia adelante para SHO

__________________________________________________________________________________________________________________________________________________

Entradas: condición inicial\(y_0 = [u_0,v_0]^T\), tiempo de finalización\(t_{end}\).

Inicializar:\(t_0 = 0, y_0\).

para\(n=0: t_{end}/h\) hacer

\({y_{n+1}} \leftarrow {A} {y_n}\)

fin para

retorno\({y_n}\).

__________________________________________________________________________________________________________________________________________________

Los resultados de una corrida utilizando este método propagador se muestran en 2.9. Los resultados son los mismos que los obtenidos en la sección 2.7

Figura 2.9: El oscilador armónico simple (SHO) integrado mediante la iteración del propagador. El uso de la matriz propagadora solo funciona cuando la ODE en consideración es lineal y cada paso puede convertirse en una multiplicación matriz-vector.

Estabilidad

Al derivar las expresiones para aproximaciones de diferencias finitas encontramos que el proceso de discretización produjo una diferencia (error) entre la derivada exacta (analítica) y la aproximación de diferencia finita. Ahora nos encontramos con un segundo escollo en la resolución numérica de ODEs: Cultivar soluciones numéricas cuando sabemos que la solución exacta (analítica) no debería crecer en el tiempo. ¿Qué está pasando?

Estabilidad del delantero Euler para el crecimiento exponencial ODE

Para entender el crecimiento observado considera el crecimiento exponencial ODE:\[\tag{eq:2.20} \frac{dy}{dt} = a y\] Tenga en cuenta que esta ODE es lineal. Sabemos que esta ecuación tiene una solución exacta, matemáticamente-verdadera\(y_t(t) = y_0 e^{a t}\), donde denotamos la solución exacta, matemáticamente-verdadera como\(y_t\). Ahora haz la pregunta: ¿Qué pasa si la solución exacta se ve perturbada por algún error\(e\)? Es decir, tomar\(y = y_t(t) + e(t)\). En este caso linealidad dice que podemos escribir\[\nonumber \frac{dy_t}{dt} + \frac{de}{dt} = a (y_t + e)\] Esta ecuación se separa en dos piezas,\[\nonumber \frac{dy_t}{dt} = a y_t\] que se satisface de manera idéntica porque\(y_t\) es la solución exacta por definición, y\[\nonumber \frac{de}{dt} = a e\] Que gobierna el comportamiento del término de error\(e\). Ahora discretiza este término usando el método forward Euler para llegar\[\tag{eq:2.21} e_{n+1} = e_n + h a e_n = (1 + a h)e_n\] donde\(e_n\) está el error en el paso\(n\). Asumiendo que comenzamos con una pequeña perturbación\(e_0\) a la vez\(t=0\), y solo vemos la evolución de esta perturbación en el tiempo, encontramos que [eq:2.21] se comporta como\[\tag{eq:2.22} e_{n} = (1 + a h)^n e_0\] Claramente, la perturbación crece exponencialmente como\(n \rightarrow \infty\) si \(\lvert 1 + a h \rvert > 1\)pero decae a cero siempre y cuando\[\tag{eq:2.23} \lvert 1 + a h \rvert < 1\] la Ecuación (2.23) sea la condición de estabilidad de Euler hacia adelante para la ODE de crecimiento exponencial. Un solucionador aplicado a una ODE es estable si un error inicial o perturbación mantiene la misma magnitud o muere en el tiempo. Pero si un error inicial crece exponencialmente, entonces el solucionador es inestable. Tenga en cuenta que la propiedad de estabilidad depende tanto del solucionador como de la propia ODE; un solucionador que es estable para una ODE podría ser inestable para otra diferente, y diferentes solucionadores pueden ser estables o inestables para la misma ODE.

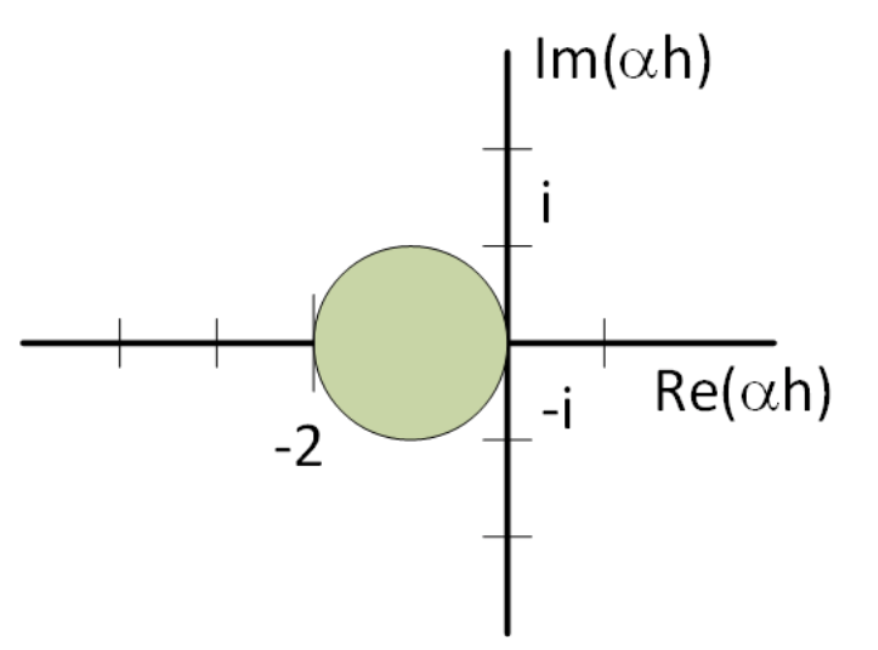
Entonces ahora la pregunta se vuelve, ¿cuándo es adelante Euler estable para la ODE simple [eq:2.20]? Para que el delantero Euler tenga sentido, el paso\(h\) debe ser un número pequeño, positivo. Sin embargo, no hemos puesto ninguna restricción en\(a\), puede ser positiva, negativa o incluso compleja. Por lo tanto, para entender cuándo [eq:2.20] es estable tiene sentido trazar la región de estabilidad en el plano complejo de\(a h\). Esto se muestra en la fig. 2.10. La región de estabilidad es el círculo gris a la izquierda del origen. Los valores dentro del círculo representan\(a h\) valores que no explotan, son estables porque satisfacen la condición de estabilidad\(\lvert 1 + a h \rvert < 1\).

Figura 2.10: Región de estabilidad de Euler hacia delante para la ODE lineal simple [eq:2.20]. La región de estabilidad para este sistema es un círculo de radio 1 en el plano complejo centrado en\(a h = -1\).

Estabilidad de Euler delantero para el oscilador armónico simple

Ahora consideramos la estabilidad del delantero Euler aplicada al oscilador armónico simple. Recordemos la iteración de Euler hacia adelante para esta ecuación,\[\begin{aligned} \begin{pmatrix} u_{n+1} \\ v_{n+1} \end{pmatrix} = \begin{pmatrix} 1 & -h k / m \\ h & 1 \end{pmatrix} \begin{pmatrix} u_{n} \\ v_{n} \end{pmatrix}\end{aligned} \tag{eq:2.24}\] Sabemos que la solución “matemáticamente-verdadera” a la SHO se compone de senos y cosenos, o equivalentemente de exponenciales complejos,\(e^{i \omega t}\). Escogeremos una solución\[\begin{aligned} \nonumber \label{eq:SHOMatVecSystem1} \begin{pmatrix} u_{n} \\ v_{n} \end{pmatrix} = \begin{pmatrix} e^{i \omega t} \\ i \omega e^{i \omega t} \end{pmatrix}\end{aligned}\] y examinaremos su evolución temporal. En lugar de considerar una perturbación aditiva, consideramos errores de seguimiento utilizando un “factor de error” multiplicativo\(e_n\). Eso significa que asumimos la solución\[\begin{aligned} \begin{pmatrix} u_{n} \\ v_{n} \end{pmatrix} = e_n \begin{pmatrix} e^{i \omega t} \\ i \omega e^{i \omega t} \end{pmatrix}\end{aligned} \tag{eq:2.25}\] y la insertamos en [eq:2.24] y vemos cómo\(e_n\) se comporta en el tiempo. Claramente, si\(e_n = 1\) para siempre, entonces [eq:2.25] resuelve [eq:2.24] exactamente. Pero si\(e_n \ne 1\) entonces la iteración de Euler hacia adelante introduce errores en la solución.

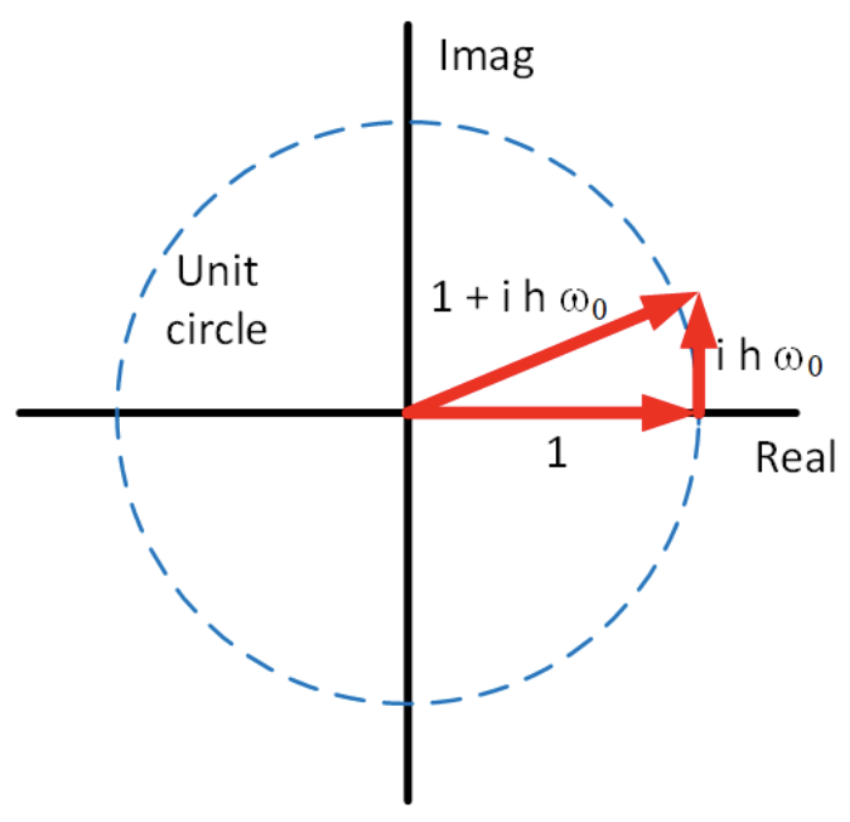
Insertando [eq:2.25] en [eq:2.24] obtenemos\[\nonumber e_{n+1} \begin{pmatrix} e^{i \omega (t+h)} \\ i \omega e^{i \omega (t+h)} \end{pmatrix} = e_n \begin{pmatrix} 1 & -\frac{h k}{m} \\ h & 1 \end{pmatrix} \begin{pmatrix} e^{i \omega t} \\ i \omega e^{i \omega t} \end{pmatrix}\] Ahora dividimos por el factor común\(e^{i \omega t}\) y definimos el llamado “factor de crecimiento”,\(g_n = e_{n+1}/e_n\) para obtener\[\nonumber g_n e^{i \omega h} \begin{pmatrix} 1 \\ i \omega \end{pmatrix} = \begin{pmatrix} 1 & -\frac{h k}{m} \\ h & 1 \end{pmatrix} \begin{pmatrix} 1 \\ i \omega \end{pmatrix}\] Ahora vemos que esta expresión tiene la forma de un problema de autovalor, \(\lambda {x} = {A} {x}\), donde el escalar\(g_n e^{i \omega h}\) juega el papel del valor propio. Podemos resolver de\(g_n e^{i \omega h}\) la manera habitual restando el LHS del RHS,\[\nonumber \begin{pmatrix} 1 - g_n e^{i \omega h} & -\frac{h k}{m} \\ h & 1 - g_n e^{i \omega h} \end{pmatrix} \begin{pmatrix} 1 \\ i \omega \end{pmatrix} = 0\] y observando que para que esto se mantenga, necesitamos valores de los\(g_n e^{i \omega h}\) cuales hagan que la matriz sea singular. Por lo tanto, requerimos\[\nonumber \begin{vmatrix} 1 - g_n e^{i \omega h} & -\frac{h k}{m} \\ h & 1 - g_n e^{i \omega h} \end{vmatrix} = 0\] o\[\nonumber (1 - g_n e^{i \omega h})^2 + h^2 \frac{k}{m} = 0\] Next, nuevamente recordamos la definición de la “frecuencia natural” de la SHO,\(\omega_0^2 = k/m\). Entonces reorganizar para resolver por\(g_n\) y obtener\[\nonumber (1 - g_n e^{i \omega h})^2 = -h^2 \omega_0^2\] o\[\nonumber g_n e^{i \omega h} = 1 \pm i h \omega_0\] Ahora preguntamos, ¿bajo qué condiciones el factor de error\(e_n\) permanece constante, o al menos no crece ni se encoge? \(e_n\)permanece constante siempre y cuando\(|g_n| = 1\). Es decir, requerimos\[\tag{eq:2.26} |g_n| = \left| 1 \pm i h \omega_0 \right|\] Sin embargo, esto claramente nunca sucede —el RHS de [eQ:FWDeulerGrowthFactor] siempre es mayor que uno. Esto es evidente al inspeccionar el RHS en el plano complejo como se muestra en la fig. 2.11. Por lo tanto, la solución calculada por adelante Euler siempre crece. Para tamaño de paso cada vez más pequeño\(h\) el factor de crecimiento tiende a 1, pero nunca llega a 1 hasta que\(h\) es exactamente cero — una situación que hace inútil el método de Euler hacia adelante ya que no se puede dar un paso adelante en el tiempo si\(h = 0\). Esto significa que el método de Euler hacia adelante nunca es útil para resolver el problema del oscilador armónico simple; necesitamos encontrar mejores métodos.

Figura 2.11: El RHS de [EQ:FWDeulerGrowthFactor]. La parte real es siempre 1, mientras que la parte imaginaria puede tomar cualquier valor. Sin embargo, siempre y cuando la parte imaginaria no sea idéntica a cero, entonces la magnitud de siempre\(1 \pm i h \omega_0\) es mayor que 1. Por lo tanto, el factor\(e_n\) de error siempre crecerá, y el SHO siempre es inestable para cualquier tamaño de paso distinto de cero\(h\).

Resumen del capítulo

Estos son los puntos importantes que se hacen en este capítulo:

• El método de Euler hacia adelante se deriva de la expresión de diferencia directa simple para la derivada,\(y' = (y_{n+1} - y_n)/h\).
• El método Euler hacia adelante es un método iterativo que comienza en un punto inicial y camina la solución hacia adelante usando la iteración\(y_{n+1} = y_n + h f(t_n, y_n)\).
• Dado que el futuro se calcula directamente utilizando valores de\(t_n\) y\(y_n\) en el presente, Euler hacia adelante es un método explícito.
• El método de Euler hacia adelante se define para las ODEs de 1er orden. Funciona tanto para ODEs de una y muchas variables. Para resolver una ODE de orden N, se rompe la ODE en N ODE de primer orden.
• El error RMS esperado al usar el método de Euler hacia adelante escala como\(e \sim O(h)\).
• La estabilidad del Solver no está garantizada para todos los tamaños de escalón\(h\). El criterio de estabilidad depende de la ODE exacta en consideración, pero en general se requieren tamaños de escalón más pequeños para la estabilidad cuando se utilizan métodos explícitos.