1.3: Método de Euler hacia atrás
- Page ID
- 118882
Algoritmo Euler
Al siguiente solucionador de ODE se le llama el “método Euler hacia atrás” por razones que rápidamente se volverán obvias. Empezar con la ODE de primer orden,\[\tag{eq:3.1} \frac{d y}{d t} = f(t, y)\] luego recordar la aproximación de diferencia hacia atrás,\[\nonumber \frac{d y}{d t} \approx \frac{y_n - y_{n-1}}{h}\] Podemos usar esto en [eq:3.1] para obtener\[\tag{eq:3.2} \frac{y_n - y_{n-1}}{h} = f(t_n, y_n)\] Ya que estamos usando la diferenciación hacia atrás para derivar [eq:3.2], este es el “método de Euler hacia atrás”. Ahora mueve esto hacia adelante en el tiempo en un paso (es decir, reemplazar\(n\) por\(n+1\) todas partes). Este cambio crea una ecuación válida ya que [eq:3.2] es válida para todos\(n\). Al cambiar obtenemos\[\nonumber \frac{y_{n+1} - y_{n}}{h} = f(t_{n+1}, y_{n+1})\] Ahora traslada el futuro al LHS y el presente al RHS para conseguir\[\tag{eq:3.3} y_{n+1} - h f(t_{n+1}, y_{n+1}) = y_{n}\] Ahora bien podrías preguntar, ¿de qué sirve esta expresión? Para poder computar lo desconocido\(y_{n+1}\), necesitas saber ya\(y_{n+1}\) para usarlo en el LHS. Pero, ¿cómo puedes usar\(y_{n+1}\) si es lo desconocido que estás resolviendo?
La respuesta es que puedes convertir [eq:3.3] en un problema de búsqueda de raíces. Restar el valor conocido\(y_n\) de ambos lados de [eq:3.3]. Entonces considere que la expresión en el LHS es una función de\(y_{n+1}\). Tenemos\[\tag{eq:3.4} g(y_{n+1}) = y_{n+1} - h f(t_{n+1}, y_{n+1}) - y_{n} = 0\] Por lo tanto, encontrar\(y_{n+1}\) implica encontrar la raíz de\(g(y_{n+1})\). En general,\(g(y_{n+1})\) puede ser una función desagradable, no lineal de\(y_{n+1}\), pero tales problemas se manejan fácilmente usando métodos numéricos — el método de Newton inmediatamente me viene a la mente. No cubriremos el rootfinding en esta clase, pero muchos métodos se presentan en los textos estándar sobre análisis numérico.
Suponiendo que puedes usar un método de búsqueda de raíces para resolver [eq:3.4], tienes un método de paso de tiempo: Comience con la condición inicial\(y_0\), insértelo en [eq:3.4], luego use el rootfinding para calcular\(y_1\). Luego usando\(y_1\) use [eq:3.4] y rootfinding para encontrar\(y_2\), y así sucesivamente. Este es el método atrasado de Euler.
El pseudocódigo que implementa el algoritmo de Euler hacia atrás para resolver el oscilador armónico simple se muestra en [alg:3]. Una representación gráfica del algoritmo se muestra en la fig. 3.1.
__________________________________________________________________________________________________________________________________________________
Método de Euler hacia atrás del algoritmo 3
__________________________________________________________________________________________________________________________________________________
Entradas: condición inicial\(y_0\), tiempo de finalización\(t_{end}\).
Inicializar:\(t_0 = 0, y_0\).
para\(n = 0: t_{end}/h\) hacer
Ecuación de forma para LHS con\(y_{n+1}\) como variable desconocida,\(g(y_{n+1}) = y_{n+1} - h f(t_{n+1}, y_{n+1}) - y_{n}\)
Resolver problema de búsqueda de raíces\(g(y_{n+1}) = 0\) para encontrar\(y_{n+1}\).
fin para
\(y\)vector de retorno.
__________________________________________________________________________________________________________________________________________________
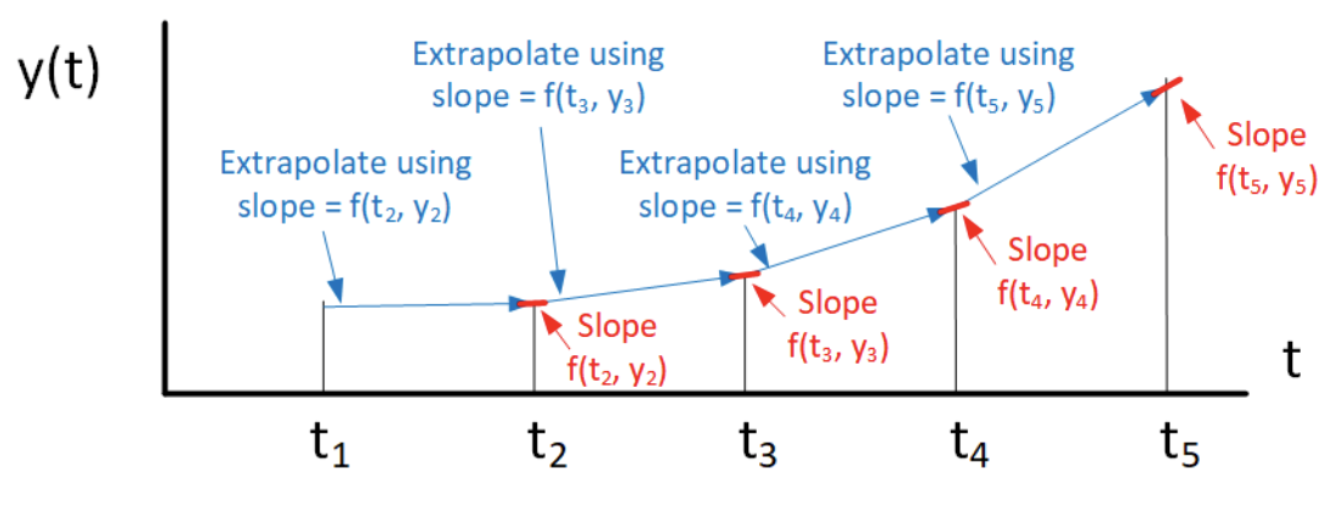
Aquí hay algunas cosas a tener en cuenta sobre el atrasado Euler:
- Tenga en cuenta que la pendiente utilizada es la pendiente al final del intervalo de escalón, de ahí el nombre “hacia atrás” Euler. Se puede ver como cada paso está determinado por la pendiente de la línea azul.
- El paso no es calculable directamente a partir del RHS de [eq:3.3]. Más bien, se requiere rootfinding para obtener el valor de\(y_{n+1}\) en cada paso. Por lo tanto, al revés Euler se le llama un “método implícito”.
Ejemplo: ODE de crecimiento exponencial
Como ejemplo de Euler hacia atrás volvemos a considerar la ODE de crecimiento exponencial,\[\tag{eq:3.5} \frac{d y}{d t} = \alpha y\] Discretizar usando la aproximación de diferencia hacia atrás para obtener\[\nonumber \frac{y_{n+1} - y_n}{h} = \alpha y_{n+1}\] Mover el futuro al LHS y el presente al RHS para obtener\[\nonumber y_{n+1} - h \alpha y_{n+1} = y_n\] Dado que esta es una ecuación lineal, derivar el método de paso de tiempo es fácil — no se requiere búsqueda de raíces. Obtenemos\[\tag{eq:3.6} y_{n+1}= \frac{y_n}{1 - h \alpha }\] una gráfica de la solución encontrada vía Euler hacia atrás cuando\(h = 0.1\) se muestra en la fig. 3.2. ¡Algo anda mal! Las parcelas no se parecen a las que se muestran en la fig. 2.3, ni coinciden con el resultado analítico. ¿Qué pasó?
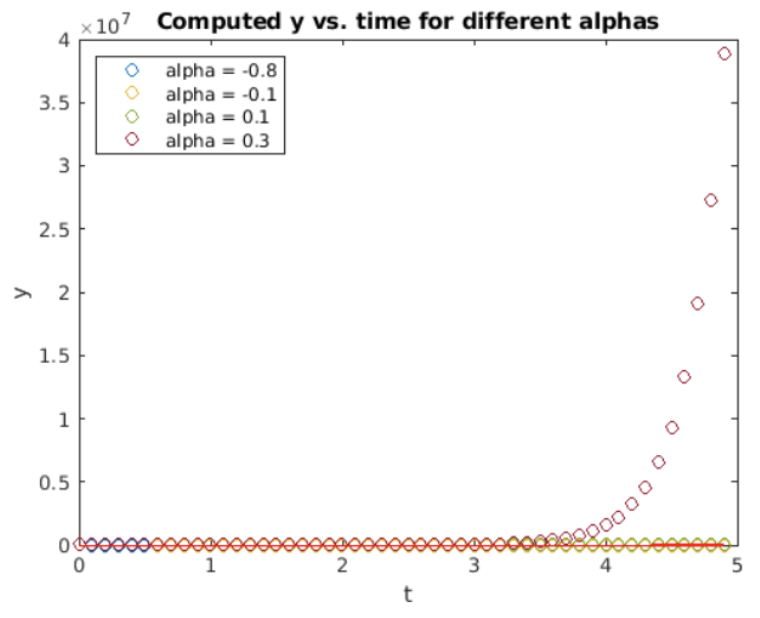
El indicio más grande es la escala del eje y —dice que una de las curvas aumenta a alrededor de 4e7—, un número gigantesco. Esta es una clara señal hacia atrás Euler es inestable para este sistema. Por lo tanto, la estabilidad es el tema de la siguiente subsección.
Estabilidad de Euler atrasado para la ODE de crecimiento exponencial
Ahora derivamos el dominio de estabilidad para el método de Euler hacia atrás. De nuevo consideramos la ecuación de crecimiento exponencial [eq:3.5] presentada por primera vez en la sección 2.2. Siguiendo un argumento similar al presentado en la sección 2.2 podemos derivar la siguiente expresión para el crecimiento de una perturbación inicial:\[\nonumber e_{n+1} = \frac{e_n}{1 + a h}\] Obsérvese la similitud de esta expresión con [eq:3.6] en la última sección. La similitud se mantiene debido a la linealidad de [eq:3.5]. Suponiendo que la perturbación de inicio en el momento\(t=0\) es\(e_0\), el error crece como\[\tag{eq:3.7} e_n = \left( \frac{1}{1+a h} \right)^n e_0\] Para que el error permanezca acotado, requerimos\[\nonumber \left| \frac{1}{1+a h} \right| \le 1\] o\[\tag{eq:3.8} \left| 1+a h \right| \ge 1\] Una gráfica de la región en el plan complejo donde el error está acotado (es decir, donde Euler hacia atrás es estable para esto ODE) se muestra en la fig. 3.3. Tenga en cuenta que esta región de estabilidad es el complemento de la obtenida para Euler hacia adelante; Euler hacia atrás es estable para grandes valores de paso relativo (grande\(a h\)) mientras que Euler delantero solo es estable para pasos pequeños. Compare las regiones de estabilidad que se muestran aquí con las que se muestran en la fig. 2.10.
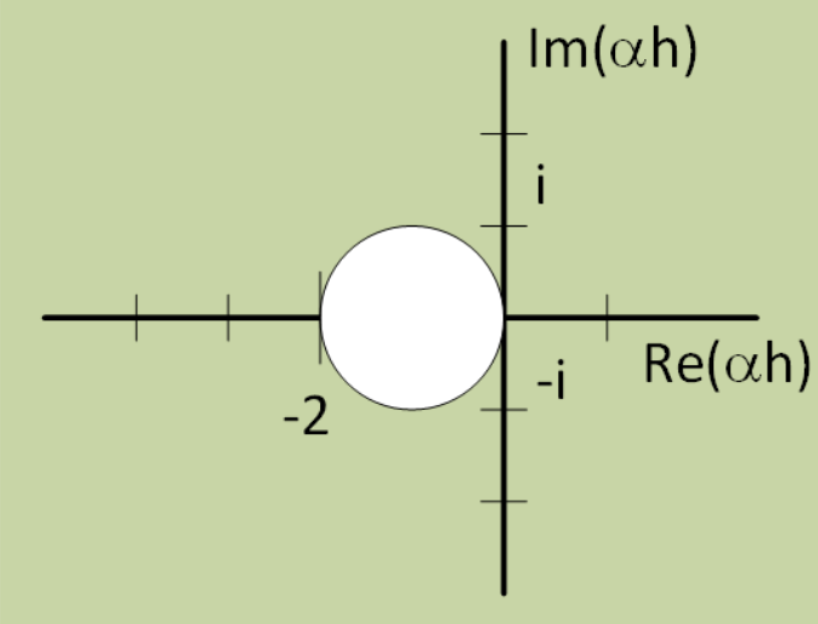
Pensando en los resultados obtenidos en la sección 3.2 para la ODE de crecimiento exponencial, recordamos que establecemos\(h = 0.1\) y simulamos una serie de\(\alpha\) valores diferentes. Por cada\(\alpha\) valor tenemos
- \(\alpha = -0.8\),\(\alpha h = -0.08\). Esto se encuentra dentro del círculo inestable en 3.3. ¡Inestable!
- \(\alpha = -0.1\),\(\alpha h = -0.01\). Esto se encuentra dentro del círculo inestable en 3.3. ¡Inestable!
- \(\alpha = 0.1\),\(\alpha h = 0.01\). Esto se encuentra fuera del círculo inestable en 3.3. Estable.
- \(\alpha = 0.3\),\(\alpha h = 0.03\). Esto se encuentra fuera del círculo inestable en 3.3. Estable.
Por lo tanto, los malos resultados que se muestran en 3.2 se deben a que dos de los\(\alpha h\) valores se encuentran en la zona inestable.
Ejemplo: la ecuación logística
Recordemos la ecuación logística, [eq:2.11]. Discretizamos para el atrasado Euler poniendo el futuro en el LHS y el presente en el RHS. En este caso la iteración es\[\nonumber y_{n+1} - h \left( 1 - \frac{y_{n+1}}{Y_m} \right)y_{n+1} = y_n\] Esta es una ecuación no lineal, por lo que se requiere un rootfinder para implementar la iteración de Euler hacia atrás. Es decir, en cada iteración se resuelve la siguiente ecuación para encontrar el valor de\(y_{n+1}\)\[\nonumber g(y_{n+1}) = y_{n+1} - h \left( 1 - \frac{y_{n+1}}{Y_m} \right)y_{n+1} - y_n = 0\] Los parámetros\(h\) y\(Y_m\) son entradas al problema y por lo tanto son cantidades conocidas. También, ya que en cada paso empezamos en\(t_n\), también\(y_n\) se conoce el valor. Eso significa que\(y_{n+1}\) es lo único desconocido y es la cantidad por la que resolvemos. Un solucionador como el método de Newton, o la función incorporada de Matlab “fsolve ()” son perfectamente adecuados para calcular el valor requerido de\(y_{n+1}\).
Esta iteración se implementó en Matlab y luego se ejecutó para tres valores diferentes de\(Y_m\). Los resultados se muestran en 3.4. La solución calculada lidera la solución analítica. Compare esto con 2.6, donde la solución calculada sigue la solución analítica.
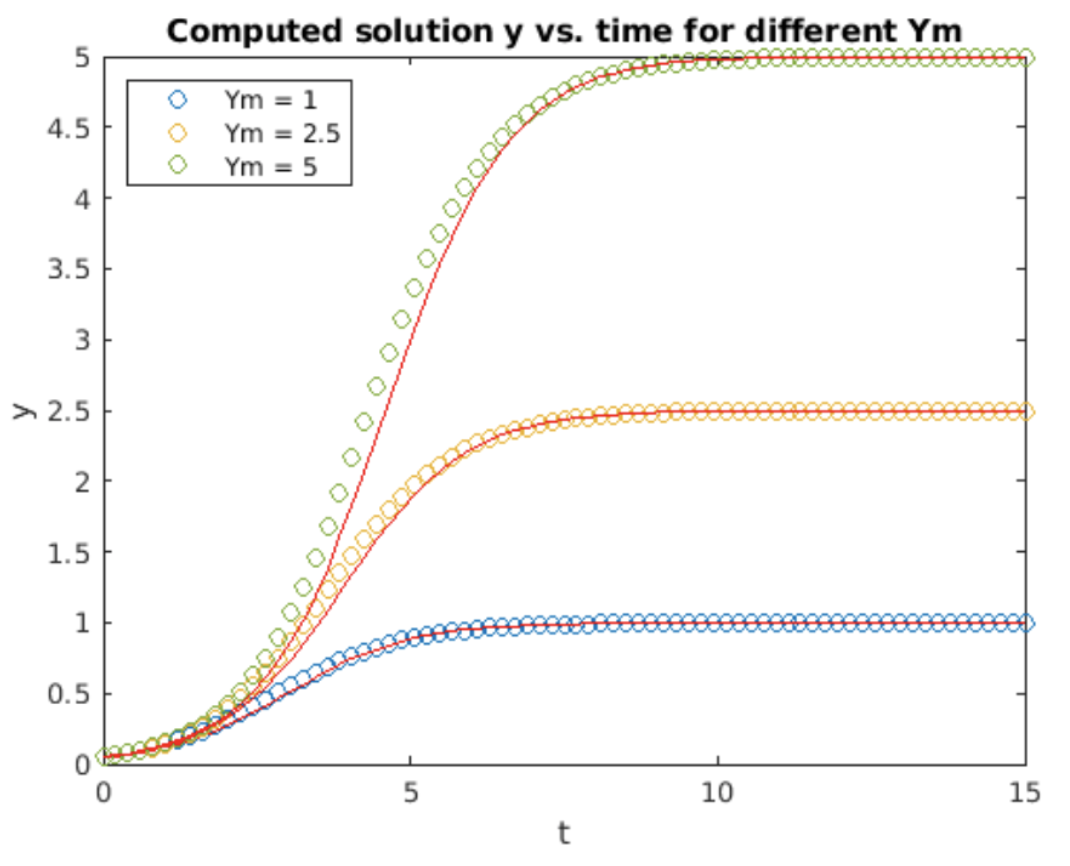
Ejemplo: el oscilador armónico simple
Para aplicar el método de Euler hacia atrás al oscilador armónico simple comenzamos con el par de ODEs de primer orden,\[\begin{aligned} \nonumber \frac{d u}{d t} &= -\frac{k}{m} v \\ \nonumber \frac{d v}{d t} &= u\end{aligned}\] luego discretizamos usando la aproximación de diferencia hacia atrás. Obtenemos\[\tag{eq:3.9} \begin{aligned} \frac{u_{n+1} - u_{n}}{h} &= -\frac{k}{m} v_{n+1} \\ \frac{v_{n+1} - v_{n}}{h} &= u_{n+1} \end{aligned}\] Reordenando y moviendo el futuro al LHS y el presente al RHS esto se convierte\[\begin{aligned} \nonumber u_{n+1} + h \frac{k}{m} v_{n+1} = u_{n} \\ \nonumber v_{n+1} - h u_{n+1}= v_{n} \end{aligned}\] Ahora podemos reunir los coeficientes sobre el LHS en una matriz y escribir esto\[\begin{aligned} \nonumber \begin{pmatrix} 1 & h k / m \\ -h & 1 \end{pmatrix} \begin{pmatrix} u_{n+1} \\ v_{n+1} \end{pmatrix} = \begin{pmatrix} u_{n} \\ v_{n} \end{pmatrix}\end{aligned}\] como Al igual que con adelante Euler, observamos que el sistema [eq:3.9] puede ser reemplazado por matriz-vector multiplicación porque la ecuación original es lineal. Si el sistema original era no lineal, entonces necesitarías resolverlo como un sistema (es decir, no podrías simplificarlo en una forma de multiplicación matriz-vector).
Queremos aislar el futuro en el LHS y usar el RHS para calcular el futuro usando cantidades conocidas. Por lo tanto, movemos la matriz al RHS para obtener la iteración,\[\begin{aligned} \begin{pmatrix} u_{n+1} \\ v_{n+1} \end{pmatrix} = \begin{pmatrix} 1 & h k / m \\ -h & 1 \end{pmatrix}^{-1} \begin{pmatrix} u_{n} \\ v_{n} \end{pmatrix}\end{aligned} \tag{eq:3.10}\] ahora hemos aislado todas las cantidades conocidas en el RHS por lo que tenemos un método de paso de tiempo. En la implementación de Matlab podríamos usar la inversa analítica de la\(2 \times 2\) matriz, pero en su lugar simplemente la dejaremos tal como está y dejaremos que Matlab realice el cálculo usando una operación de resolución lineal. Esto está en el espíritu de Euler hacia atrás, donde cada paso del algoritmo implica invertir la función [eq:3.4] que aparece en el LHS. En este caso, la función es la multiplicación matriz-vector, por lo que solo necesitamos invertir la matriz (es decir, hacer una resolución lineal) para moverla al RHS.
Al ejecutar el algoritmo SHO de Euler hacia atrás se obtiene la gráfica mostrada en 3.5. En este caso encontramos que las oscilaciones sinusoidales decaen con el tiempo. Para un escalón más pequeño\(h\) el decaimiento es más lento que para mayor\(h\). Nuevamente, este comportamiento no es consistente con la solución analítica, que es una onda sinusoidal que tiene amplitud constante —es decir, sin incremento ni decaimiento con el tiempo.
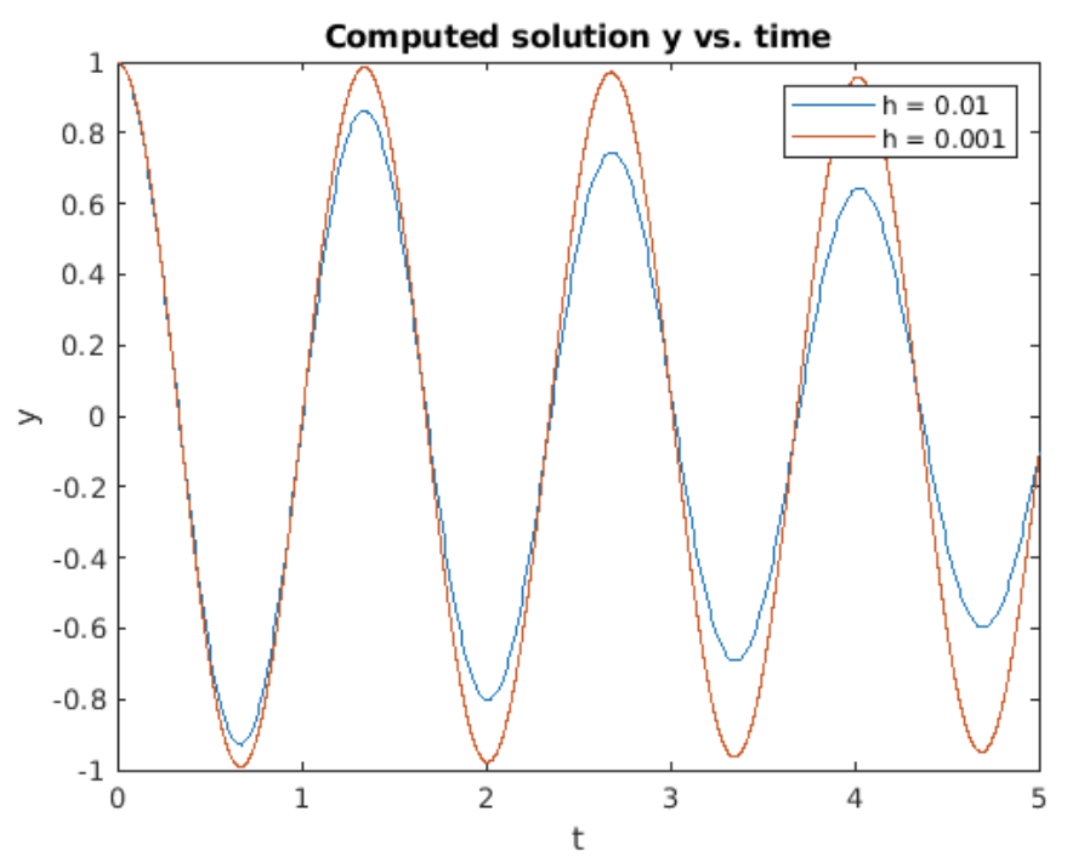
Estabilidad de Euler hacia atrás para el oscilador armónico simple
Entender por qué la solución decae implica encontrar los valores propios de la matriz propagadora. Es decir, emprenderemos un análisis de estabilidad para Euler atrasado similar al presentado en 2.9.2 para el delantero Euler. Para hacer la vida más fácil primero definiremos\[\tag{eq:3.11} \omega^2 = \frac{k}{m}\] Esto solo hace que el álgebra sea más fácil después. A continuación, invertimos la matriz en el RHS de [eq:3.10]. Esto nos da la matriz propagadora\[\nonumber \begin{pmatrix} \frac{1}{h^2 \omega^2 + 1} & - \frac{h \omega^2}{h^2 \omega^2 + 1} \\ \frac{h}{h^2 \omega^2 + 1} & \frac{1}{h^2 \omega^2 + 1} \end{pmatrix}\] Para entender la estabilidad de la iteración debemos examinar los valores propios de la matriz propagadora [eq:3.11]. Llamar a los valores propios\(g\) para “factor de crecimiento”. Los valores propios de esta matriz se encuentran resolviendo\[\nonumber det \begin{pmatrix} \frac{1}{h^2 \omega^2 + 1} - g & - \frac{h \omega^2}{h^2 \omega^2 + 1} \\ \frac{h}{h^2 \omega^2 + 1} & \frac{1}{h^2 \omega^2 + 1} -g \end{pmatrix} =0\] para\(g\). Tenemos\[\nonumber \left(\frac{1}{h^2 \omega^2 + 1} - g \right)^2 + \frac{h^2 \omega^2}{(h^2 \omega^2 + 1)^2} = 0\] así\[\nonumber g = \frac{1 \pm i h \omega}{h^2 \omega^2 + 1}\] o\[\tag{eq:3.12} g = \frac{1}{1 \pm i h \omega}\] Ahora consideramos la magnitud (valor absoluto) de\(g\). El numerador de [eq:3.12] es uno mientras que el denominador siempre tiene valor absoluto menor que uno. Por lo tanto,\(|g| < 1\) siempre a menos que\(h=0\) o\(\omega=0\). \(h=0\)no es un valor útil ya que implica no pisar. Por lo tanto, para cualquier valor razonable de\(h \omega\) la solución obtenida por Euler hacia atrás siempre disminuirá para cualquier tamaño de paso distinto de cero\(h\), como se observa en 3.5.
Resumen del capítulo
Estos son los puntos importantes que se hacen en este capítulo:
- El método de Euler hacia atrás se deriva de la simple expresión de diferencia hacia atrás para la derivada,\(y' = (y_{n} - y_{n-1})/h\).
- El método Euler hacia atrás es un método iterativo que comienza en un punto inicial y camina la solución hacia adelante usando la iteración\(y_{n+1} - h f(t_{n+1}, y_{n+1}) = y_{n}\).
- Dado que el futuro\(y_{n+1}\) aparece como una función que debe invertirse en el LHS, Euler hacia atrás es un método implícito.
- Como cualquier método implícito, se requiere un rootfinder —como el método de Newton— para encontrar\(y_{n+1}\) en cada paso en el tiempo.
- El error RMS esperado al usar el método Euler hacia atrás se escala como\(e \sim O(h)\).
- La estabilidad del Solver no está garantizada para todos los tamaños de escalón\(h\). El criterio de estabilidad depende de la ODE exacta en consideración, pero Euler delantero puede ser estable para tamaños de escalón más grandes que Euler delantero.


