1.4: Métodos predictor-corrector y Runge-Kutta
- Page ID
- 118894
Método de Heun
El siguiente solucionador de ODE es el método de Heun. Utiliza un nuevo enfoque para computar el mejor paso a dar desde la posición actual\((t_n, y_n)\). Para apreciar mejor el método de Heun, primero revisemos los problemas experimentados por los dos métodos estudiados hasta ahora:
- Delantero Euler. En adelante Euler calculamos la pendiente de\(y(t)\) en el momento actual\(t_n\) y usamos esa pendiente para dar un paso adelante hacia el futuro. El problema con Euler delantero es que la función\(f(t, y)\) podría curvarse alejándose de la línea predicha por la pendiente en\(t_n\). En consecuencia, la precisión del delantero Euler es\(O(h)\) —que es baja.
- Atrás Euler. Hacia atrás Euler utiliza la pendiente en el momento\(t_{n+1}\) para calcular el paso hacia adelante. Una vez más, sin embargo, la solución\(y(t)\) puede curvarse alejándose de la línea predicha por la pendiente en\(t_{n+1}\), por lo que la precisión vuelve a ser baja.
El problema con ambos métodos es que utilizan una aproximación lineal al comportamiento de la solución dentro del intervalo\(t_n \le t \le t_{n+1}\), y utilizan una pendiente calculada al final del intervalo. El método de Heun intenta solucionar este problema conservando la aproximación lineal, pero promediando las pendientes de ambos extremos del dominio. Específicamente, el método de Heun hace lo siguiente:
- Sentarse\(t=t_n\) y calcular la pendiente en este punto,\(s_1 = f(t_n, y_n)\).
- Utilice esta pendiente para estimar el valor de la solución\(t_{n+1}\) usando Euler delantero estándar:\(\tilde{y}(t_{n+1}) = y(t_n) + h f(t_n, y_n)\). Tenga en cuenta que denotamos este punto\(\tilde{y}(t_{n+1})\) usando una tilde\(\sim\) ya que es un paso intermedio hacia nuestra solución.
- En este punto\((t_n, \tilde{y}_{n+1})\) computar la pendiente\(s_2 = f(t_{n+1}, \tilde{y}_{n+1})\).
- Promedio de estas dos pendientes para calcular el paso de avance:\[\tag{eq:4.1} y(t_{n+1} ) = y(t_n) + \frac{h}{2} \left( s_1 + s_2 ) \right)\]
El método todavía asume una aproximación en línea recta a\(y(t)\) en el intervalo\(t_n \le t \le t_{n+1}\) pero utiliza una mejor aproximación a la pendiente. El algoritmo formal se presenta en [alg:4]. Este proceso se muestra gráficamente en 4.1.
__________________________________________________________________________________________________________________________________________________
Algoritmo 4 Método de Heun
__________________________________________________________________________________________________________________________________________________
Entradas: condición inicial\(y_0\), tiempo de finalización\(t_{end}\).
Inicializar:\(t_0 = 0, y_0\).
para\(n=0: t_{end}/h\) hacer
Calcular pendiente en\(t_n\):\(S_1 \leftarrow f(t_n, y_n)\)
Calcular paso intermedio en\(t_{n+1}\):\(\tilde{y} \leftarrow y_n + h S_1\)
Calcular pendiente en\(t_{n+1}\):\(S_2 \leftarrow f(t_{n+1}, \tilde{y})\)
Calcular paso final:\(y_{n+1} \leftarrow y_n + (h/2)(S_1 + S_2)\)
fin para
\(y\)vector de retorno.
__________________________________________________________________________________________________________________________________________________
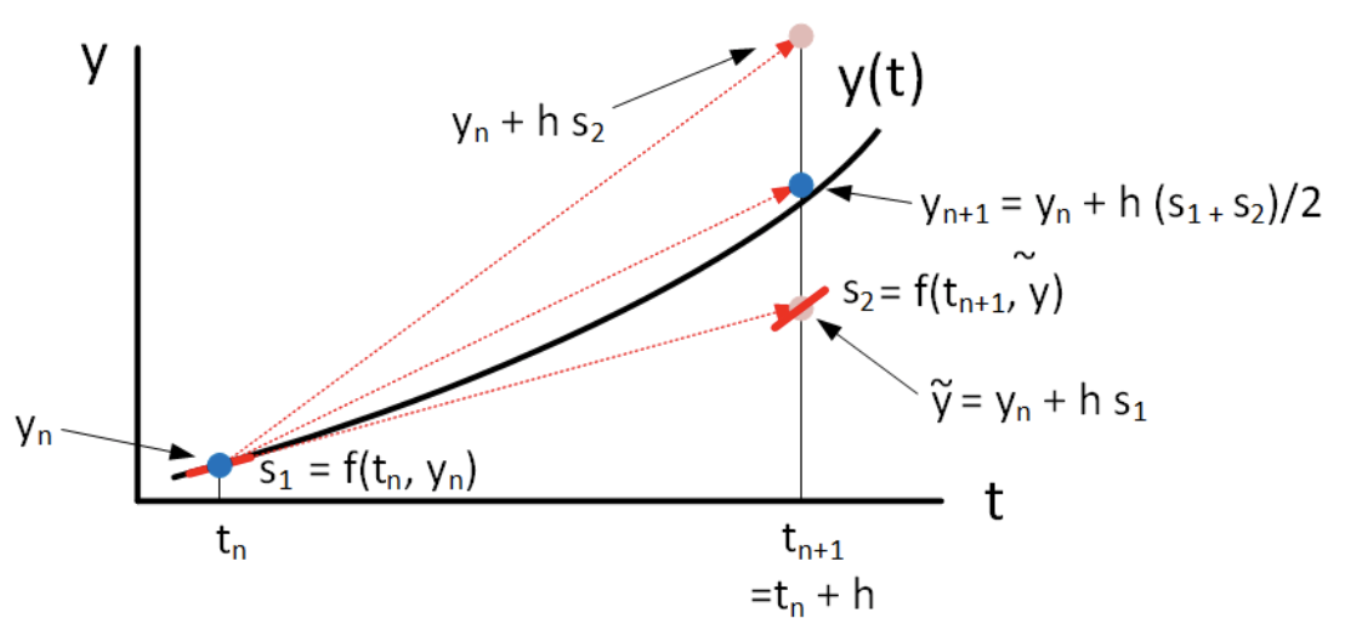
La trama muestra el resultado de la computación\(y_{n+1}\) usando Euler hacia adelante y hacia atrás, así como el método de Heun. Lo que hay que observar es que para la curvatura de función mostrada, Euler hacia adelante infravalora el valor real de la función en\(y_{n+1}\) y hacia atrás Euler lo sobrepasa. No obstante, dado que el método de Heun promedia las pendientes presentes y (adivinadas) futuras, se acerca mucho más a alcanzar el valor correcto deseado de\(y_{n+1}\).
El método de Heun es quizás el solucionador de ODE más básico en una gran familia de solucionadores que se denominan métodos “predictor-corrector”. La idea es que estos métodos primero den uno o más pasos de “predictor” hacia el futuro, luego usen los resultados de los pasos predictores para calcular el “corrector” — el paso real. En el caso del método de Heun tenemos:
- Predictor:\(\tilde{y} = y_n + h f(t_n, y_n)\)
- Corrector:\(y_{n+1} = y_n + (h/2)(f(t_n, y_n) + f(t_{n+1}, \tilde{y}))\)
En cierto sentido, estos\(y\) valores intermedios se utilizan para “sentir” lo que se ve la pendiente en el futuro. Una vez que se han dado suficientes pasos de prueba (paso predictor), entonces se combinan entre sí (paso corrector) para formar el paso final.
Ejemplo: la ODE de crecimiento exponencial y el escalado de errores
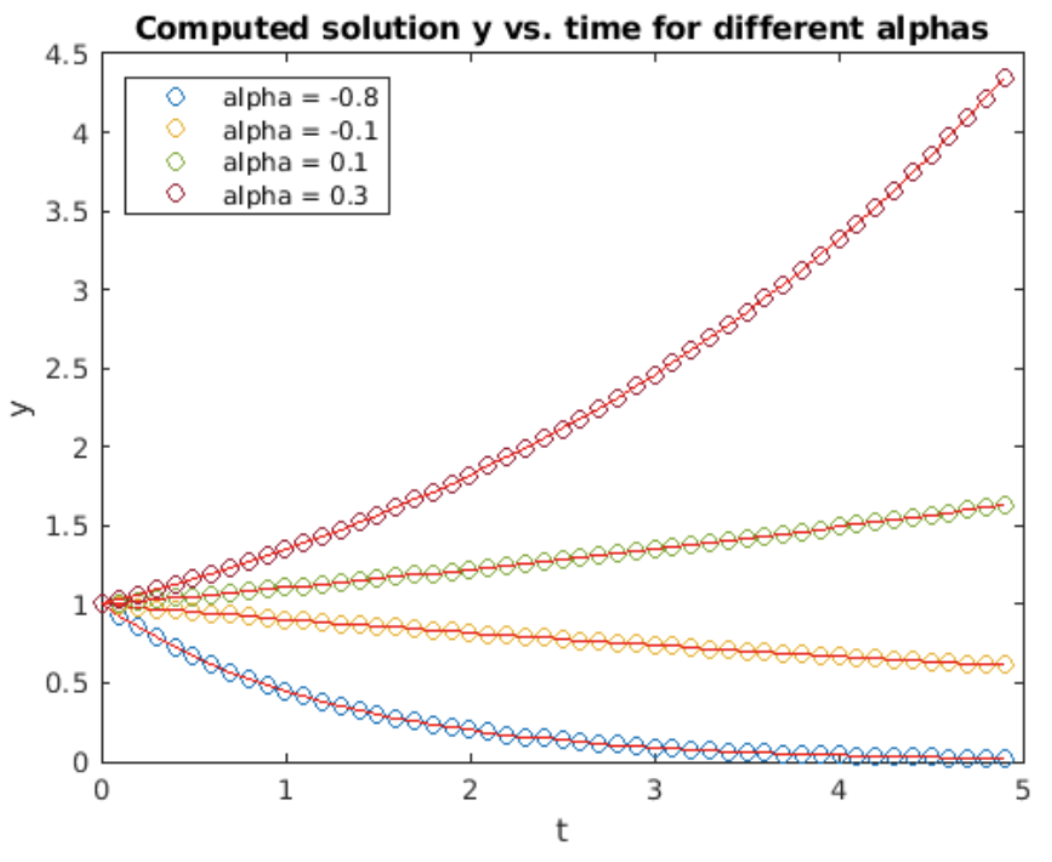
Como es habitual, examinamos el resultado de usar el método de Heun en la ODE de crecimiento exponencial, [eq:2.5]. Los resultados de la simulación se muestran en la fig. 4.2. La solución calculada claramente da una mejor coincidencia con los resultados analíticos — ¡el método de Heun es un método mejor que el de adelante Euler!
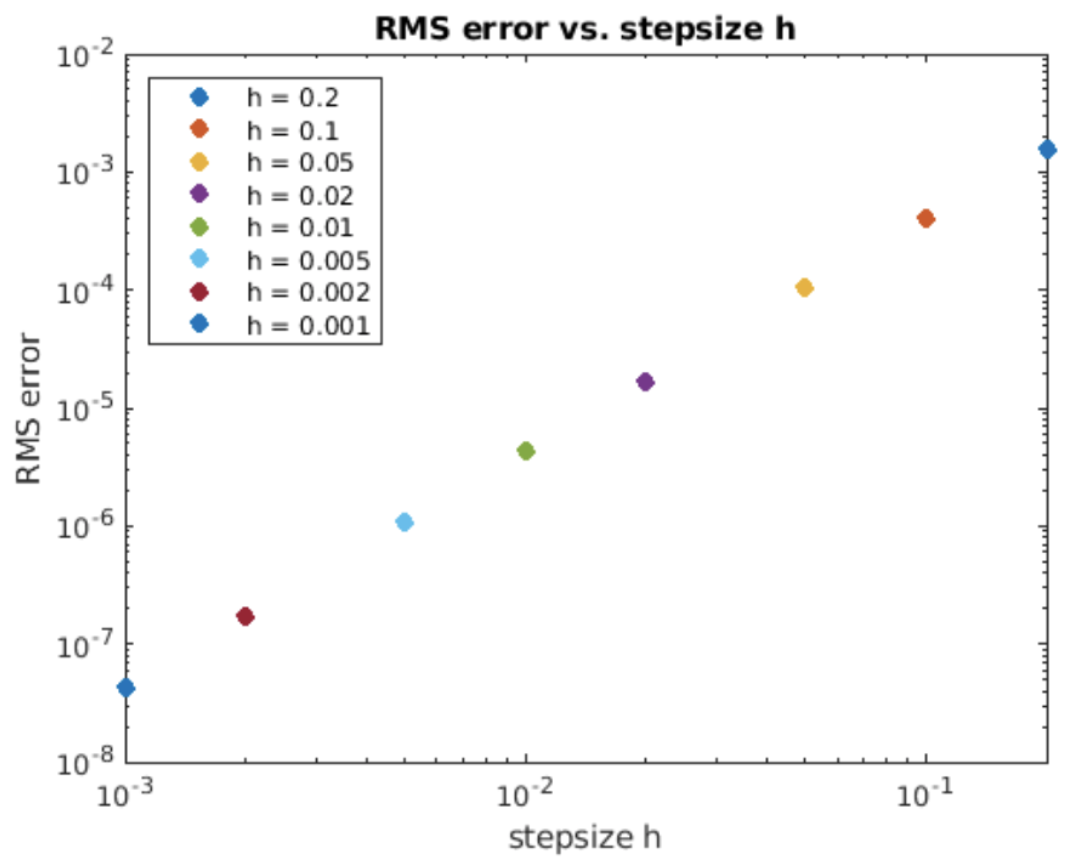
Podemos cuantificar la precisión del método de Heun calculando el error RMS entre las soluciones calculadas y analíticas para diferentes estepsias\(h\). Esto se muestra en 4.3. En una gráfica logarítmica, la pendiente de la línea de error es dos; el orden del método de Heun es en consecuencia\(O(h^2)\). Es decir, si reducimos a la mitad el tamaño del paso entonces obtenemos un factor de cuatro mejora en la precisión del método. Esto es mucho mejor que la\(O(h)\) precisión que ofrece el delantero Euler.
Ejemplo: el oscilador armónico simple
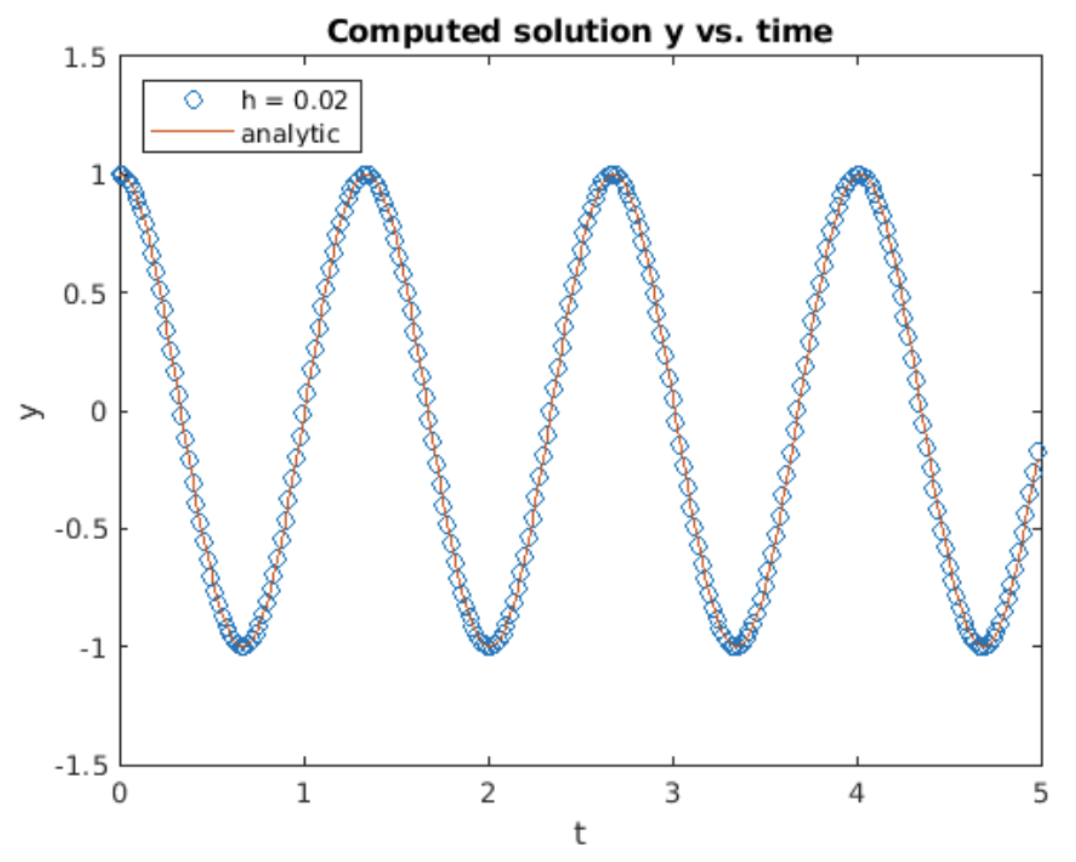
Nuestro amigo, el oscilador armónico simple, también es fácil de implementar usando el método de Heun. El resultado de ejecutar el método de Heun usando un tamaño de paso mayor que el utilizado para Euler hacia adelante y hacia atrás se muestra en 4.4. En comparación con Euler tanto hacia adelante como hacia atrás, la oscilación no crece ni decae significativamente durante el tiempo de simulación de 5 segundos, al menos en la escala de 4.4. Esto sugiere que el método de Heun es un algoritmo superior tanto a Euler hacia adelante como hacia atrás. La mejor precisión es el resultado del uso de información de pendiente tanto de tiempo\(t_n\) como\(t_{n+1}\) — esto le da al método un\(h^2\) orden. Sin embargo, no todo es color de rosa — ver 4.5 que traza la diferencia entre la solución calculada y la analítica. La diferencia evidentemente crece exponencialmente, aunque la magnitud no es tan mala como con los métodos de Euler.
Método de punto medio
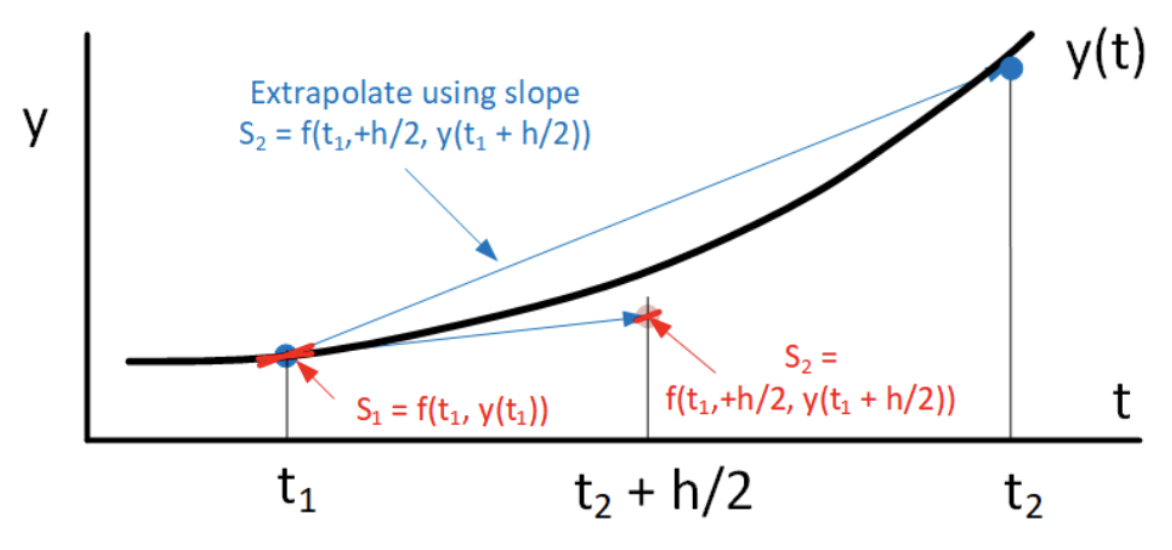
Un método similar al de Heun es el método del punto medio. Analizaremos específicamente el método explícito del punto medio (también hay un método implícito del punto medio). El método de punto medio utiliza Euler hacia adelante para dar medio paso adelante, luego calcula la pendiente en ese punto y usa esa pendiente para hacer el paso completo. El algoritmo se presenta en [alg:5]. Un dibujo que muestra cómo funciona el método del punto medio se muestra en 4.6.
__________________________________________________________________________________________________________________________________________________
Algoritmo 5 Método de punto medio
__________________________________________________________________________________________________________________________________________________
Entradas: condición inicial\(y_0\), tiempo de finalización\(t_{end}\).
Inicializar:\(t_0 = 0, y_0\).
para\(n=0: t_{end}/h\) hacer
Calcular pendiente en\(t_n\):\(s_1 \leftarrow f(t_n, y_n)\)
Calcular paso intermedio para\(t_{n} + h/2\):\(\tilde{y} \leftarrow y_n + (h/2) s_1\)
Calcular pendiente en\(t_{n} + h/2\):\(s_2 \leftarrow f(t_{n}+h/2, \tilde{y})\)
Calcular paso final:\(y_{n+1} \leftarrow y_n + h s_2\)
fin para
\(y\)vector de retorno.
Ejemplo: la ODE de crecimiento exponencial
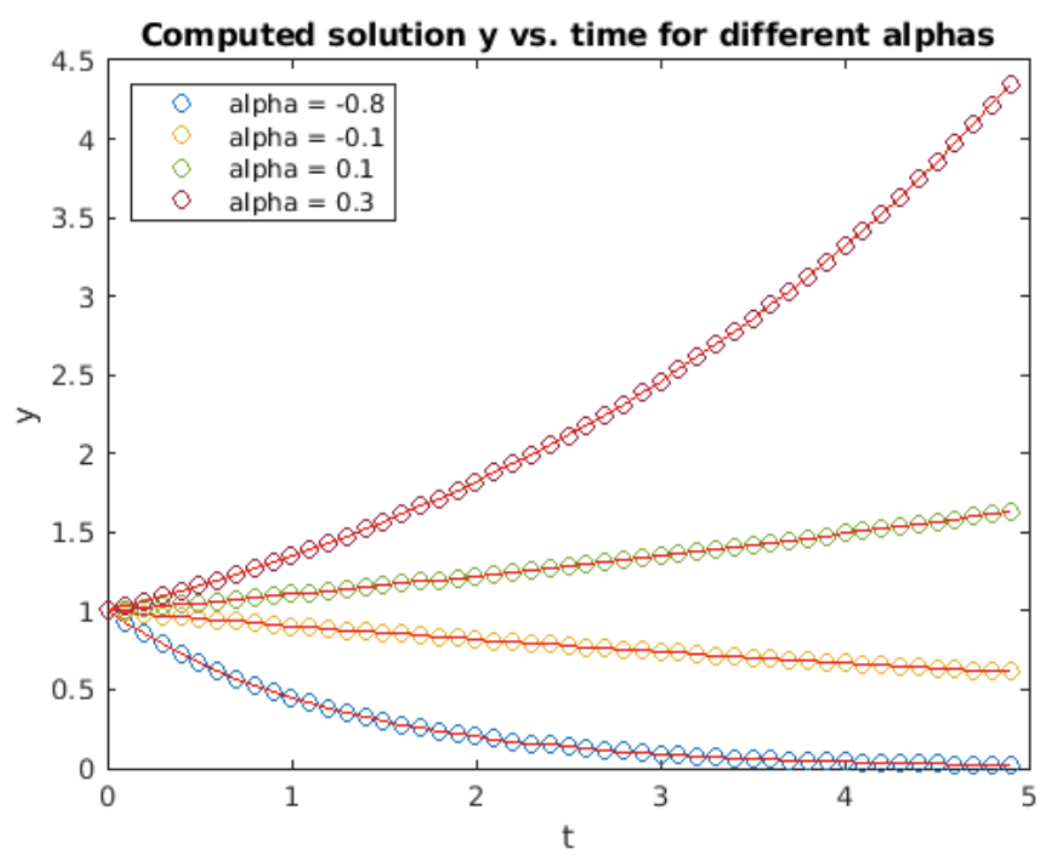
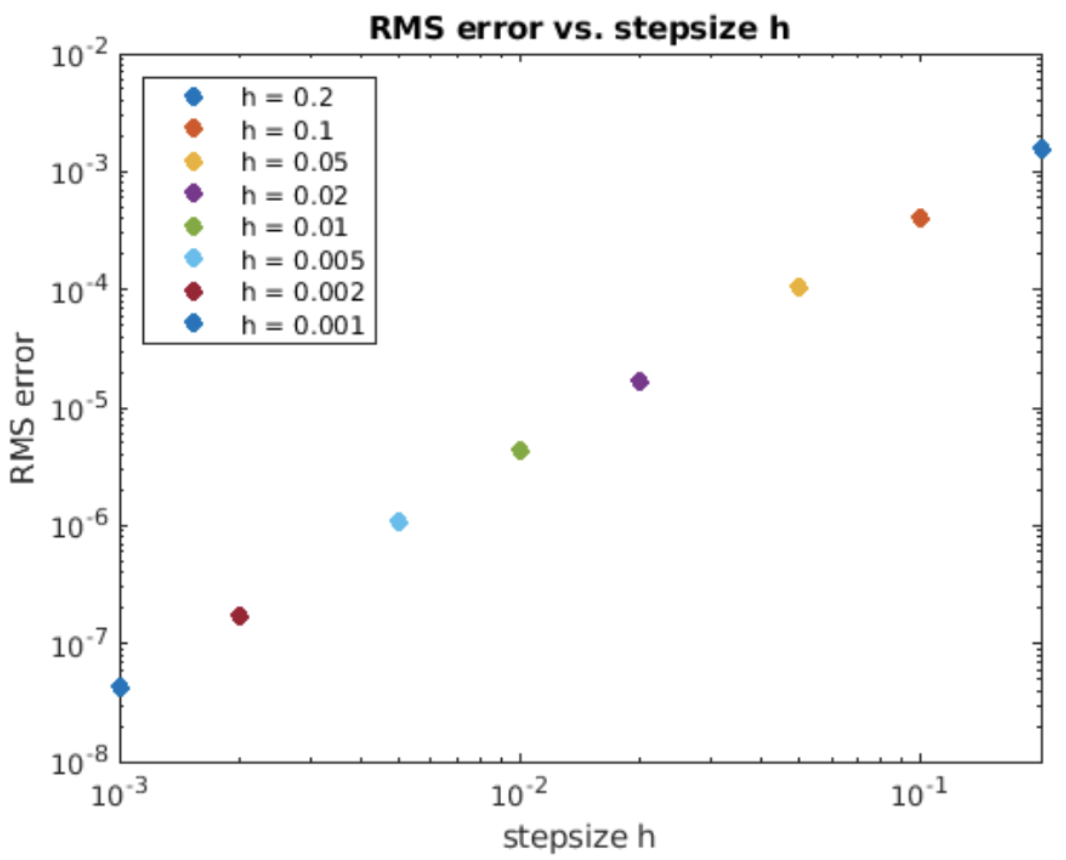
Examinamos el método del punto medio en la ODE de crecimiento exponencial, [eq:2.5]. Los resultados de la simulación se muestran en 4.7. La solución calculada claramente da una mejor coincidencia con los resultados analíticos que hacia adelante Euler: ¡el método del punto medio también es un método mejor que Euler hacia adelante! La gráfica de error RMS vs tamaño de paso se muestra en 4.8. En una gráfica log-log la pendiente de la línea de error es dos — esto dice que el orden del método es\(O(h^2)\).
Métodos Runge-Kutta
Los métodos predictor-corrector más famosos son los métodos Runge-Kutta. Incluso si en el pasado solo ha tenido familiaridad pasajera con los métodos numéricos para las ODE, probablemente haya escuchado de estos métodos, ¡o incluso los haya usado! En particular, Runge-Kutta de 4to orden es el caballo de batalla más común utilizado para resolver ODEs. Es el solucionador de referencia utilizado para resolver la mayoría de las ODE. Una variante de Runge-Kutta de 4to orden está integrada en Matlab como la función ode45. Hay muchos otros solucionadores de ODE disponibles, pero uno generalmente prueba primero Runge-Kutta de 4to orden, y si no funciona o produce malos resultados, entonces uno recurre a otros métodos más especializados.
Nos concentraremos en el clásico método Runge-Kutta de 4to orden ya que es el más común. También existen métodos Runge-Kutta de otros órdenes, pero este método de 4to orden es el más común y también muestra todos los conceptos relevantes que debes aprender. En cualquier caso, probablemente llamarás a un solucionador preescrito de una biblioteca en tu trabajo real, por lo que lo importante que debes aprender son los conceptos involucrados, no los detalles de todas y cada una de las variantes de la familia Runge-Kutta.
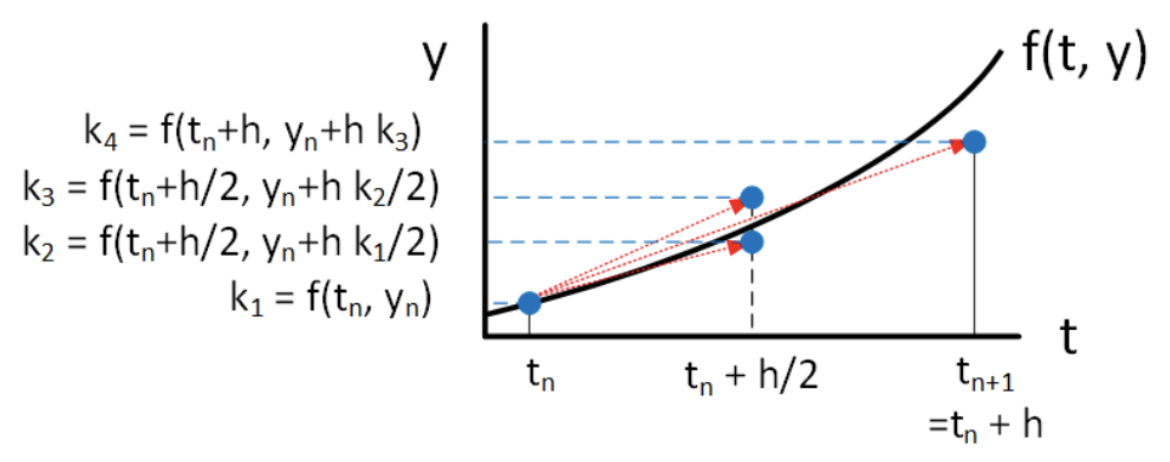
En lo que sigue llamaremos a esta variante particular del 4to orden Runge Kutta “RK4" por brevedad. RK4 toma cuatro muestras de las pendientes presentes y futuras. Aquí está el método:\[\begin{aligned} \nonumber k_1 &= h f(t_n, y_n) \\ \nonumber k_2 &= h f(t_n+h/2, y_n + k_1/2) \\ \nonumber k_3 &= h f(t_n+h/2, y_n + k_2/2) \\ \nonumber k_4 &= h f(t_n+h, y_n + k_3) \\ \nonumber y_{n+1} &= y_n + (k_1 + 2 k_2 + 2 k_3 + k_4)/6\end{aligned}\] Cosas a tener en cuenta sobre RK4:
- RK4 calcula cuatro resultados intermedios,\(k_1\),\(k_2\),\(k_3\),\(k_4\). Cada resultado intermedio se basa en el cálculo anterior, lo que significa que debe realizar los cálculos en orden. El cálculo se representa gráficamente en 4.9.
- El resultado final es una suma ponderada de los resultados intermedios.
- RK4 es un método explícito: no se requiere búsqueda de raíces para calcular el resultado deseado.
- Quizás te preguntes de dónde provienen los puntos de muestra y los coeficientes en la suma ponderada. La respuesta corta es, son algo que buscas en un libro (o en línea). La respuesta más larga es, por supuesto que pueden derivarse, pero la derivación es larga y tediosa y no da ninguna idea del método. Por lo tanto, aquí nos saltaremos la derivación.
- Hemos representado como\(y\) un escalar en lo anterior —es decir, asumimos que estamos resolviendo una sola ODE escalar. Sin embargo, al igual que en los métodos anteriores, también\(y\) puede ser un vector, es decir, RK4 también se puede usar para resolver un sistema de ODEs de la misma manera que se puede usar para todos los métodos anteriores.
Ejemplo: la ODE de crecimiento exponencial
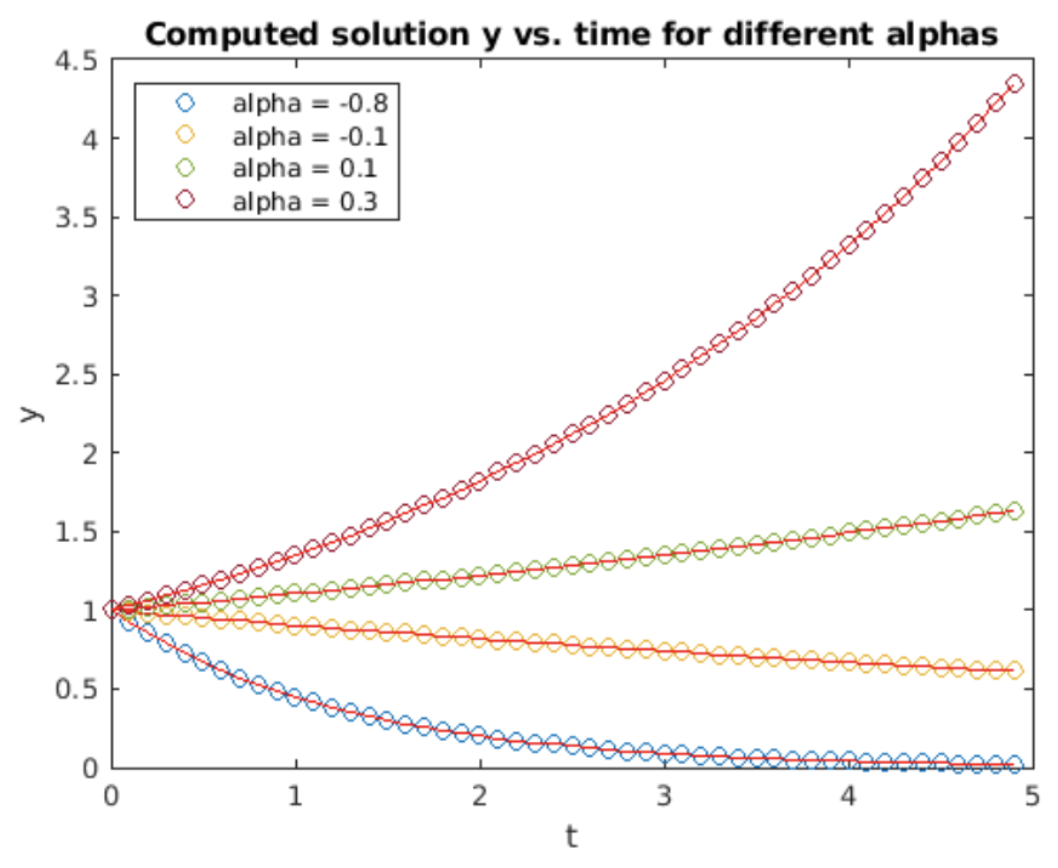
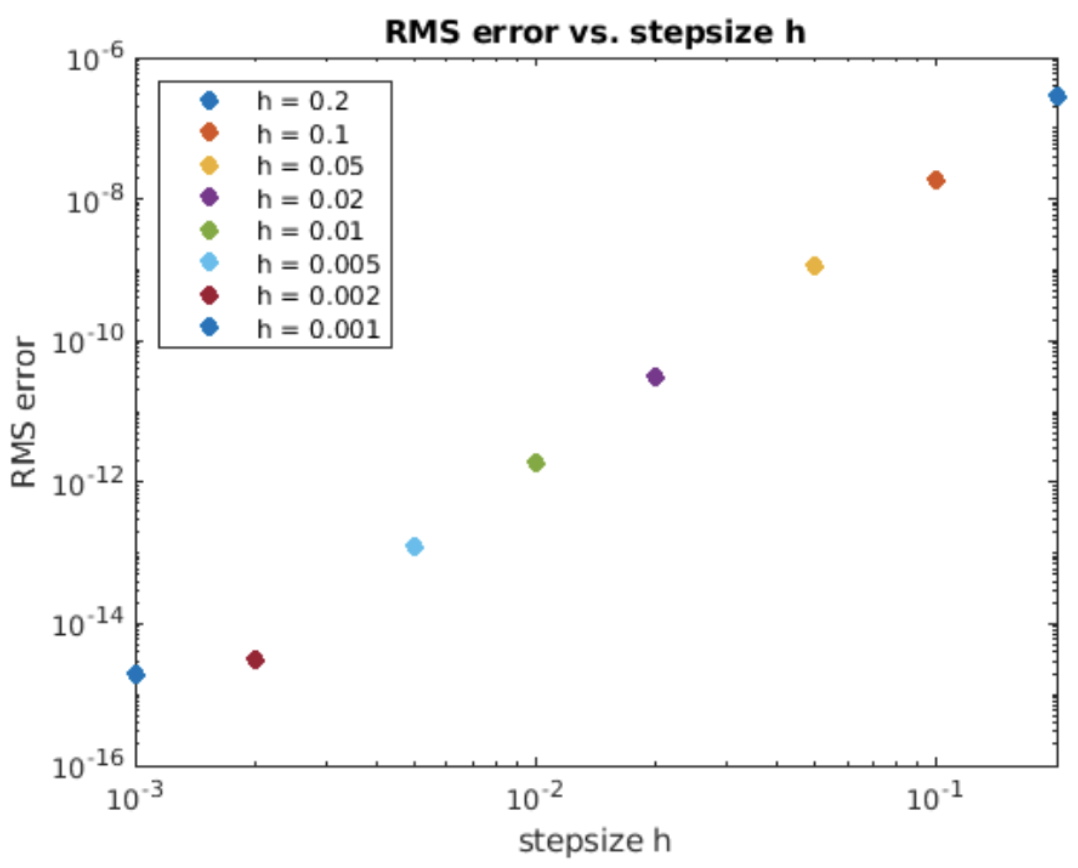
Examinamos usando RK4 en la ODE de crecimiento exponencial habitual, [eq:2.5]. Los resultados de la simulación se muestran en 4.10. La solución calculada coincide estrechamente con el resultado analítico. La gráfica de error RMS vs tamaño de paso se muestra en 4.11. Esta vez la pendiente en una parcela log-log es cuatro — esto dice que el orden del método es\(O(h^4)\).
Ejemplo: el oscilador armónico simple
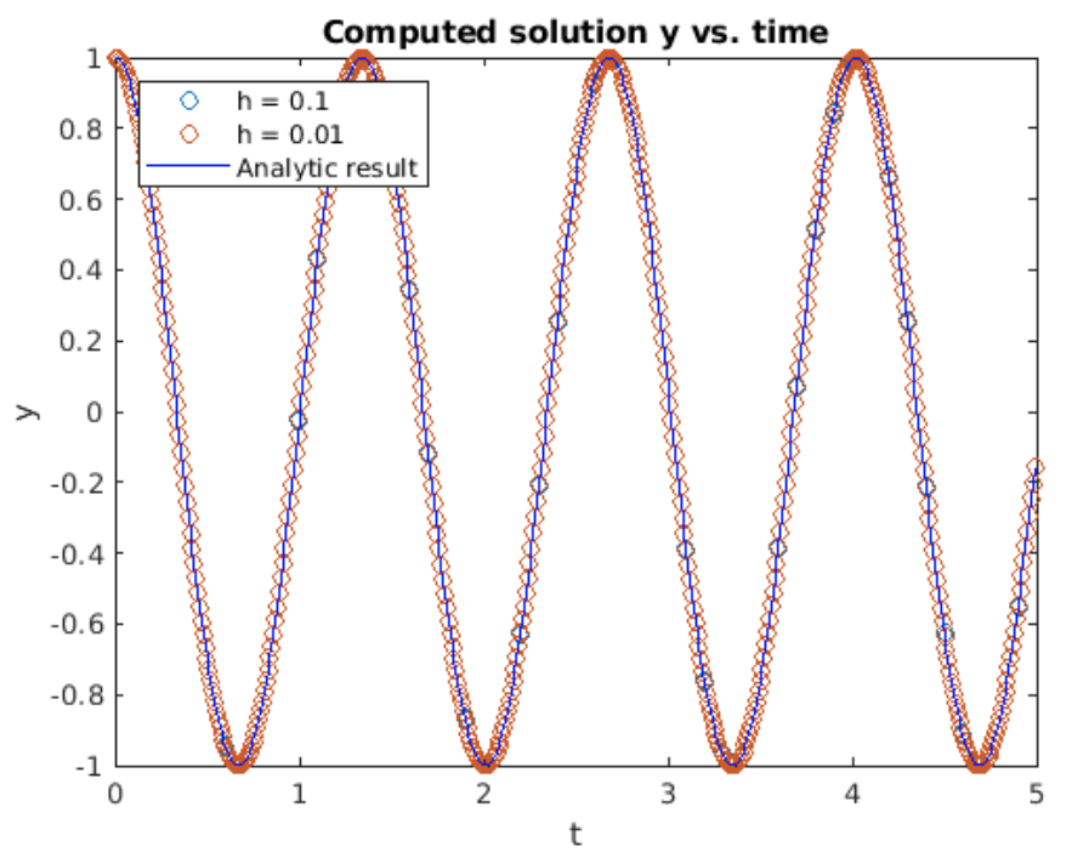
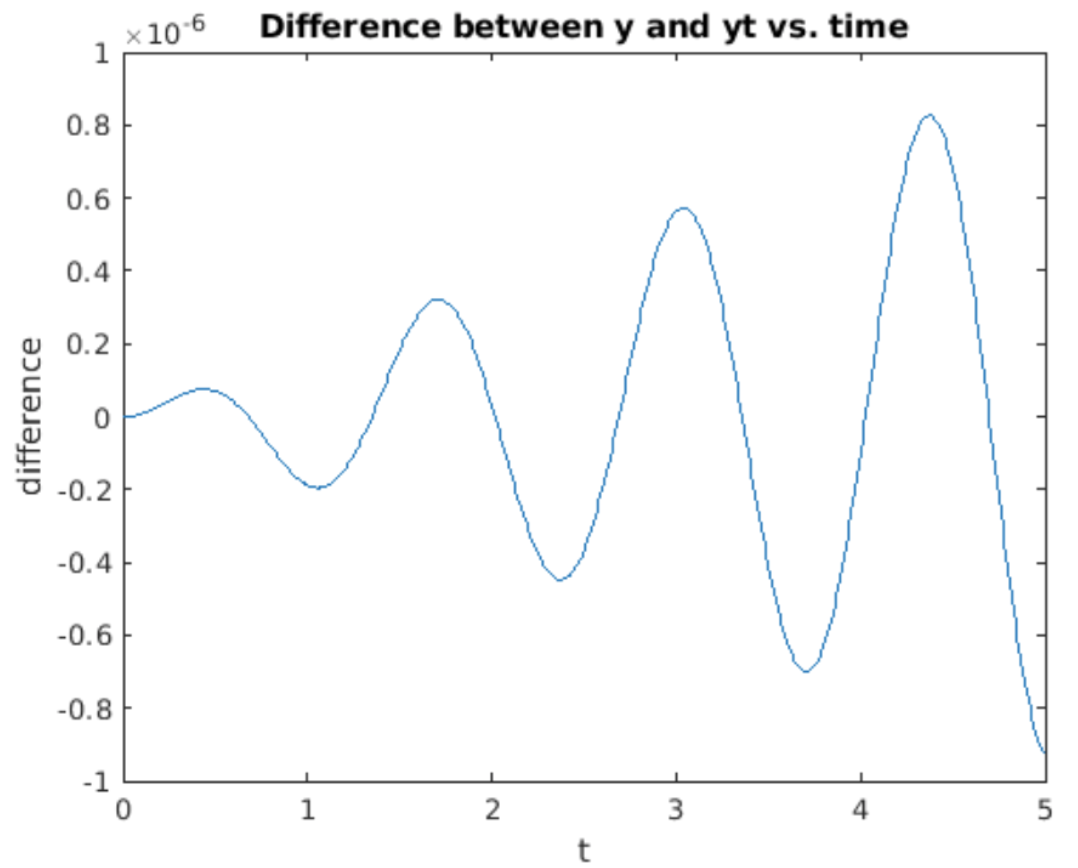
Exploremos usando RK4 usando nuestro viejo amigo el SHO. Una vez más desglosado en dos ODEs de primer orden, el SHO es\[\begin{aligned} \nonumber \frac{d u}{d t} &= -\frac{k}{m} v \\ \nonumber \frac{d v}{d t} &= u\end{aligned}\] Para usar RK4 escribimos esto en la forma general\[\begin{aligned} \frac{d u}{d t} &= f(t, u, v) \\ \frac{d v}{d t} &= g(t, u, v) \end{aligned} \tag{eq:4.2}\] con\(f(t, u, v) = -(k/m) v\) y\(g(t, u, v) = u\). Para implementar este método en la computadora tratamos todas las variables como vectores. Es decir, recogemos la expresión de LHS como\[\nonumber y = \begin{pmatrix} du/dt \\ dv/dt \end{pmatrix}\] y el RHS como\[\nonumber F = \begin{pmatrix} f(t, u, v) \\ g(t, u, v) \end{pmatrix}\] así el sistema vectorizado a integrar es\[\nonumber \frac{dy}{dt} = F(t, y)\] Entonces cada uno de los pasos intermedios\(k_i\) es un vector de\(2 \times 1\) columna. Escribir el problema de esta manera facilita la implementación de RK4 usando expresiones vectorizadas. Los resultados obtenidos para integrar el SHO usando RK4 se muestran en 4.12 junto con el resultado analítico\(\cos(\omega t)\). Los resultados se ven geniales, ambos\(h = 0.1\) y\(h=0.01\) producen ondas coseno que se ven perfectas, al menos a lo largo de la escala y el período de tiempo simulado. Sin embargo, los resultados no son perfectos — 4.13 muestra la diferencia (error) entre los resultados calculados y analíticos. Aunque la diferencia es pequeña, es diferente de cero. Peor aún, el error crece exponencialmente con el aumento del tiempo. Esto sugiere que el método RK4 —como Euler hacia adelante y hacia atrás— es inestable para el oscilador armónico simple, aunque mucho mejor que los otros métodos.
Ejemplo: el péndulo colgante
Hemos empleado el oscilador armónico simple como ejemplo útil para demostrar los diferentes solucionadores encontrados hasta ahora. El SHO se utiliza a veces como un modelo linealizado del movimiento de un péndulo colgante. Sin embargo, el movimiento de un péndulo colgante real se rige por una ODE no lineal. La geometría del problema se muestra en 4.14.
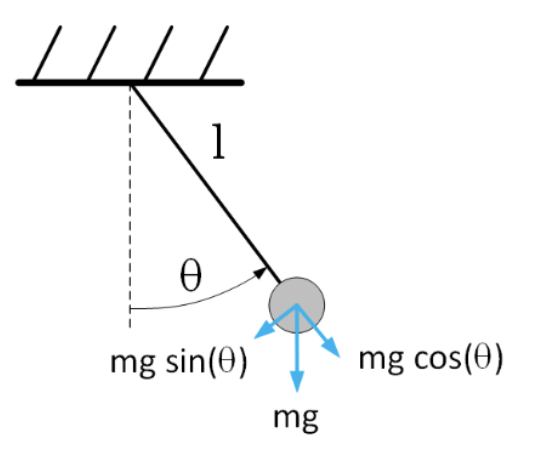
La variable independiente es el tiempo\(t\), la variable dependiente (que queremos resolver) es el ángulo que\(\theta\) hace el péndulo con respecto a la vertical. La longitud del péndulo es\(l\) y la constante de fuerza gravitacional es\(g\). La ODE se deriva de la siguiente manera:
- Consideramos las fuerzas que actúan sobre el péndulo cuando es desplazado de la vertical por un ángulo\(\theta\). En particular, la gravedad tira del péndulo hacia abajo con una fuerza vertical constante\(m g\).
- La fuerza vertical puede resolverse en dos componentes: uno en la\(\hat{r}\) dirección —en línea con el soporte del péndulo, y otro en la\(\hat{\theta}\) dirección. Trigonometría elemental dice que la fuerza en la\(\hat{\theta}\) dirección es\(F_{\theta} = -m g \sin(\theta)\). El signo negativo aparece ya que la fuerza tira de la sacudida del péndulo hacia el punto de equilibrio en\(\theta = 0\).
- Dice la segunda ley de Newton\(F = m a\). En el caso del bob del péndulo,\(F\) es la fuerza que actúa en la\(\hat{\theta}\) dirección, y\(a\) es la aceleración en la\(\hat{\theta}\) dirección. Dado que el bob de péndulo está unido a la varilla de longitud\(l\), la aceleración angular es\(l d^2 \theta / d t^2\).
- Usando la información anterior, la ecuación que rige el movimiento del péndulo es\[\nonumber m l \frac{d^2 \theta}{d t^2} = -m g \sin(\theta)\] o\[\tag{eq:4.3} \frac{d^2 \theta}{d t^2} = -\frac{g}{l} \sin(\theta)\]
Observe que para pequeños\(\theta\) podemos aproximarnos\(\sin(\theta) \approx \theta\) lo que devuelve el SHO. Pero para grandes oscilaciones de péndulo esta aproximación no funciona y necesitamos usar la expresión completa y no lineal para la fuerza restauradora sobre el bob del péndulo. En este caso existe una solución analítica para [eq:4.3] — la solución analítica puede expresarse usando las funciones elípticas de Jacobi sn y cn. Sin embargo, en lugar de jugar con funciones trascendentales superiores, solo usaremos RK4 para calcular las soluciones numéricamente.
Para proceder, dividimos la ODE de segundo orden [eq:4.3] en dos ODE de primer orden. Obtenemos\[\begin{aligned} \nonumber \frac{du}{dt} &= v \\ \nonumber \frac{dv}{dt} &= -\frac{g}{l} \sin(u)\end{aligned} \label{eq:NonlinearPendEqTwoODEs}\] Ahora reorganizamos este sistema en una forma vectorial para su uso con la implementación de Runge-Kutta. Obtenemos\[\begin{aligned} \begin{pmatrix} du/dt \\ dv/dt \end{pmatrix} = \begin{pmatrix} v \\ -(g/l) \sin(u) \end{pmatrix} \end{aligned} \tag{eq:4.4}\] Este formulario está listo para su implementación. La forma vectorizada [eq:4.4] se implementa en una función llamada por el propio integrador RK4, y un envoltorio de prueba es el programa principal ejecutado por el usuario. Esta es la arquitectura de software habitual mostrada anteriormente en 2.2.
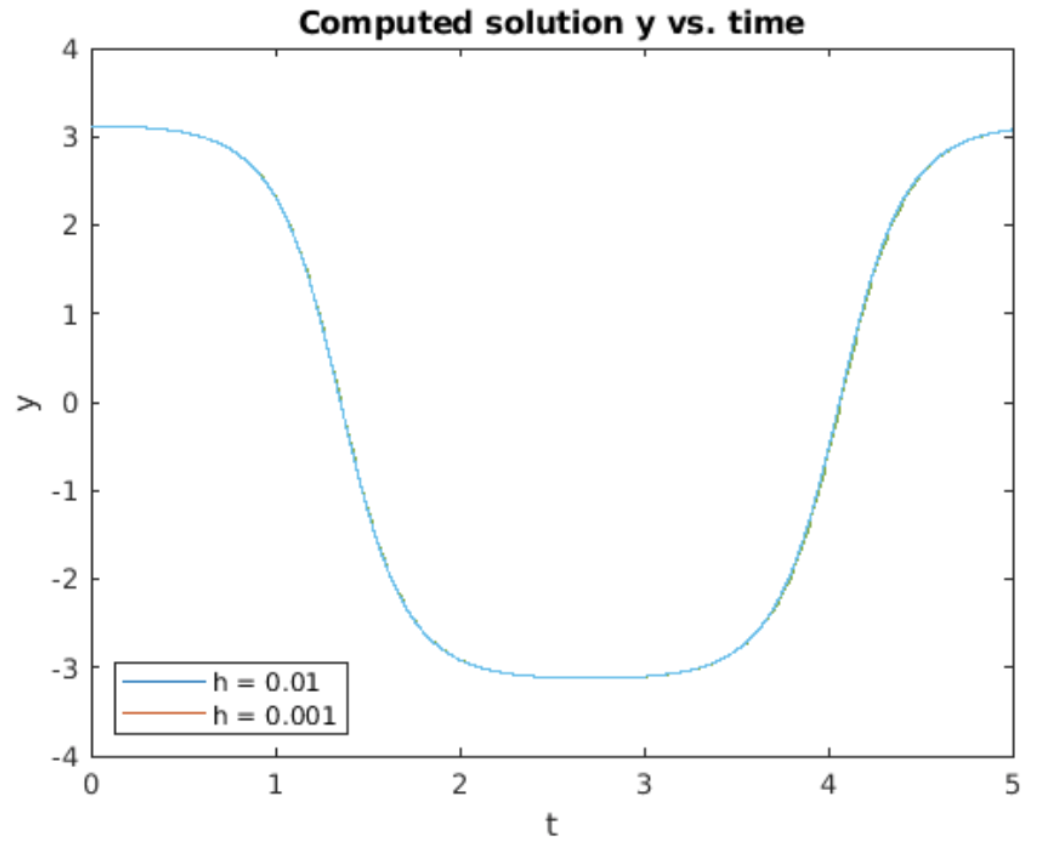
Al ejecutar la implementación de RK4 se obtiene la gráfica que se muestra en 4.15. Esta parcela se obtuvo usando\(g = 9.8\) m/seg\(^2\) (el valor de\(g\) en la superficie terrestre) y\(l = 0.5\) m, un valor razonable para la longitud de un péndulo. Para las condiciones iniciales, la oscilación del péndulo comenzó con el bob apuntando casi verticalmente hacia arriba. Por lo tanto, el péndulo tarda mucho en acelerar el bob. Luego se balancea rápidamente alrededor de la posición colgada hacia abajo y continúa hasta apuntar de nuevo casi verticalmente hacia arriba. El péndulo repite entonces este movimiento una y otra vez, sin detenerse nunca porque la ecuación original no incluye ninguna disipación (fricción).
Ejemplo: el oscilador Van der Pol
En el 1920, el físico holandés Balthasar van der Pol fue empleado por Philips para trabajar en tubos de vacío. Los tubos de vacío fueron dispositivos electrónicos utilizados para amplificar señales en los días previos a los transistores. Van der Pol encontró que bajo ciertas circunstancias los tubos de vacío oscilarían espontáneamente por sí mismos. Las autooscilaciones incontroladas son un comportamiento muy indeseable, por lo que le interesó entender por qué sucedieron. Van der Pol investigó las razones físicas de la oscilación y determinó que la oscilación de voltaje a través del tubo de vacío podría ser modelada por la ODE de segundo orden\[\tag{eq:4.5} \frac{d^2 y}{d t^2} - \epsilon(1 - y^2)\frac{d y}{d t} + y = 0\] donde\(y\) está el voltaje a través del tubo. El\(\epsilon\) término representa una amortiguación no lineal ya que implica el\(d y/d t\) término. Cuando\(y < 1\) este término representa amplificación: imparte un valor positivo a\({d^2 y}/{d t^2}\) cuando también\({d y}/{d t}\) es positivo, con lo que aumenta la amplitud de la oscilación. Cuando\(y > 1\) sucede lo contrario: el término agrega un valor negativo a\({d^2 y}/{d t^2}\) para positivo\({d y}/{d t}\) haciendo que la amplitud de la oscilación disminuya. Por lo tanto, la acción del\(\epsilon\) término es crear una oscilación cuya amplitud permanezca delimitada en el tiempo.
Esta ODE de segundo orden puede dividirse en dos ODEs de primer orden definiendo\[\begin{aligned} \nonumber u &= y \\ \nonumber v &= \frac{d y}{d t}\end{aligned}\] Entonces, el sistema ODE es\[\begin{aligned} \label{eq:VanDerPolOscSystem} \nonumber \frac{d u}{d t } &= v \\ \nonumber \frac{d v}{d t} &= \epsilon(1 - u^2) v - u\end{aligned}\]
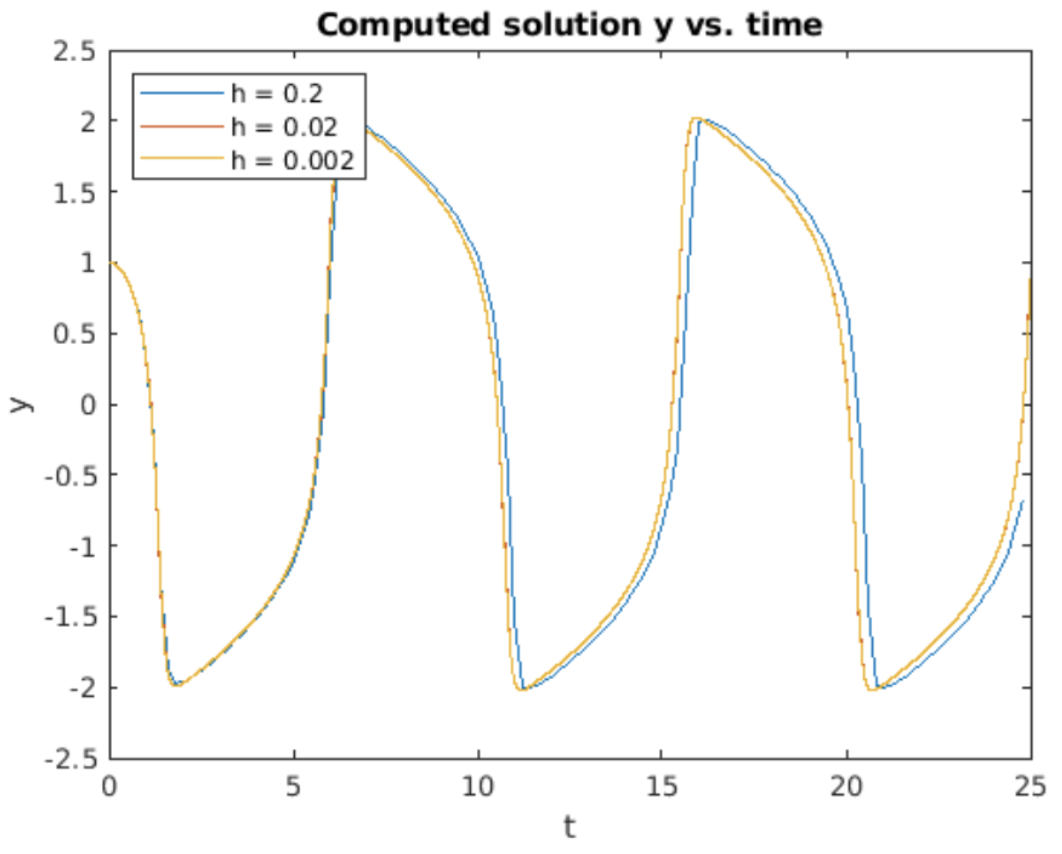
La integración de este sistema usando RK4 da la gráfica mostrada en 4.16. Cosas a tener en cuenta sobre los resultados mostrados en 4.16:
- Como se predijo, después de una fase de arranque rápido, la ODE Van der Pol produce una amplitud constante, oscilación periódica. Observamos que la oscilación no se parece en nada a las habituales oscilaciones de pecado o coseno producidas por los osciladores lineales. La fuerte no linealidad introducida por el\(dy/dt\) término es la razón de detrás de esta forma.
- Obsérvese que la\(h=0.2\) curva se desplaza de las curvas generadas con\(h\) valores menores. Este es un efecto real. es una llamada ODE “rígida”, que dificulta la resolución numérica, al menos usando tamaños de escalón más grandes. Esta propiedad se detallará en la sección 5.3 a continuación.
Ejemplo: Ecuación de Duffing
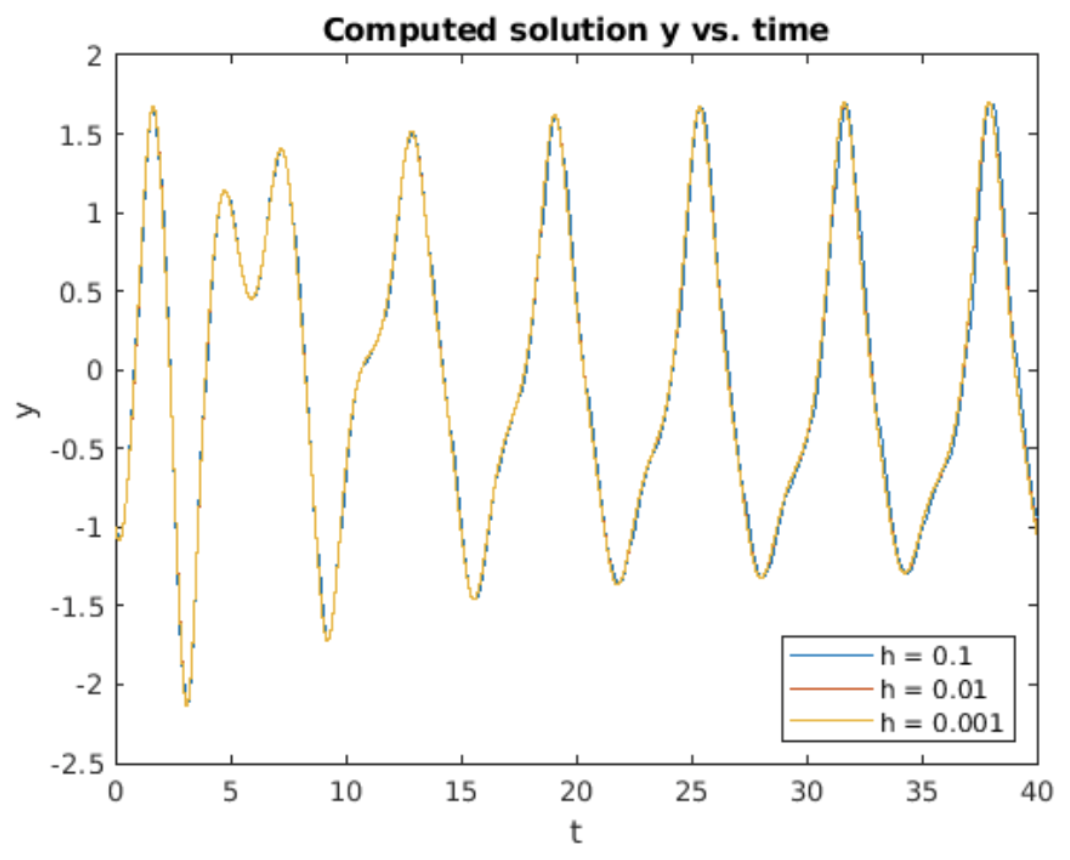
La ecuación de Duffing es una variante no lineal del oscilador armónico simple. Modela la situación en la que la respuesta del resorte no es lineal para todas las extensiones, sino que la fuerza restauradora del resorte crece más rápido que linealmente en los extremos del recorrido del resorte. Esto modela el comportamiento real de los resortes: los resortes no se comportan linealmente si se tira del resorte hasta el final de su extensión. La ecuación de Duffing modela la rigidez agregando un término cúbico a la fuerza restauradora. Para desplazamientos pequeños la fuerza cúbica es pequeña, pero para desplazamientos más grandes dominará la fuerza de retorno. En el RHS, Duffing también agrega una fuerza motriz —en este caso una unidad coseno de frecuencia\(\omega\). En 4.17 se muestra un dibujo de la configuración física. La ecuación completa de Duffing es\[\tag{eq:4.6} \frac{d^2 y}{d t^2} + \delta \frac{d y}{d t} + \alpha y + \beta y^3 = \gamma \cos(\omega t)\]
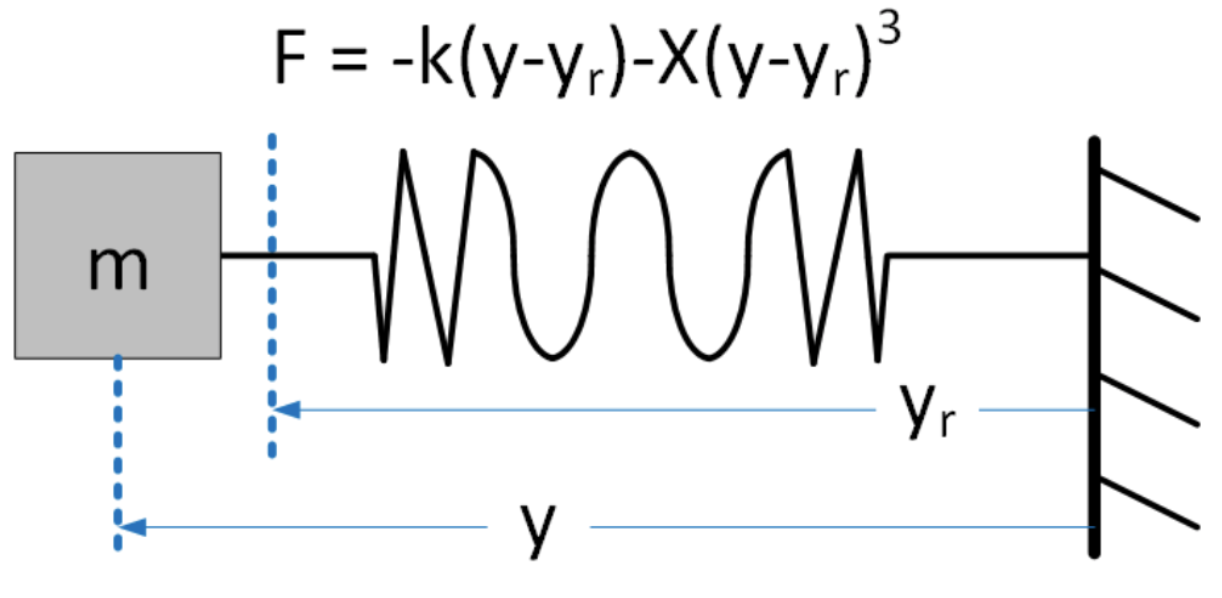
Carnicero tableaux
Como se mencionó anteriormente, existen muchas variantes diferentes del método Runge-Kutta en sí, así como otros tipos de métodos predictor-corrector. Un dispositivo útil que cataloga los diferentes métodos son los cuadros carniceros. Se trata de tablas que resumen los diferentes coeficientes que conforman un método particular. Un método predictor-corrector general y explícito se ve así:\[\begin{aligned} k_1 =& h f(t_n, y_n) \\ k_2 =& h f(t_n + c_2 h, y_n + a_{21} k_1) \\ k_3 =& h f(t_n + c_3 h, y_n + a_{31} k_1 + k_{32} k_2) \\ & \vdots \\ y_{n+1} =& y_n + \left( b_1 k_1 + b_2 k_2 + b_3 k_3 + \cdots \right) \end{aligned} \tag{eq:4.7}\] Compare esto con la definición de RK4 que se muestra arriba. Un cuadro de carnicero resume los coeficientes como se muestra el [tab:4.1].
| \(c_1\) | \(a_{11}\) | \(a_{12}\) | \(a_{13}\) | \(\cdots\) |
| \(c_2\) | \(a_{21}\) | \(a_{22}\) | \(a_{23}\) | \(\cdots\) |
| \(c_3\) | \(a_{31}\) | \(a_{32}\) | \(a_{33}\) | \(\cdots\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\ddots\) |
| \(b_1\) | \(b_2\) | \(b_3\) | \(\cdots\) |
Como ejemplos, los cuadros Butcher para el método de Heun, el método de punto medio y RK4 se muestran en [tab:4.2] - [tab:4.4]. Compara los coeficientes de las tablas con las definiciones de los métodos del solver para ver cómo están relacionados.
| 0 | 0 | 0 |
| 1 | 1 | 0 |
| 1/2 | 1/2 |
\[\begin{aligned} \nonumber k_1 &= h f(t_n, y_n) \\ \nonumber k_2 &= h f(t_n+h, y_n + k_1) \\ \nonumber y_{n+1} &= y_n + k_1/2 + k_2/2 \end{aligned}\]
Cuadro 4.2: Método de Heun
| 0 | 0 | 0 |
| 1/2 | 1/2 | 0 |
| 0 | 1 |
\[\begin{aligned} \nonumber k_1 &= h f(t_n, y_n) \\ \nonumber k_2 &= h f(t_n+h/2, y_n + k_1/2) \\ \nonumber y_{n+1} &= y_n + k_2 \end{aligned}\]
Tabla 4.3: Método del punto medio
| 0 | 0 | 0 | 0 | 0 |
| 1/2 | 1/2 | 0 | 0 | 0 |
| 1/2 | 0 | 1/2 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1/6 | 1/3 | 1/3 | 1/6 |
\[\begin{aligned} \nonumber k_1 &= h f(t_n, y_n) \\ \nonumber k_2 &= h f(t_n+h/2, y_n + k_1/2) \\ \nonumber k_3 &= h f(t_n+h/2, y_n + k_2/2) \\ \nonumber k_4 &= h f(t_n+h, y_n + k_3) \\ \nonumber y_{n+1} &= y_n + (k_1 + 2 k_2 + 2 k_3 + k_4)/6 \end{aligned}\]
Cuadro 4.4: Runge-Kutta de cuarto orden
Resumen del capítulo
Estos son los puntos importantes que se hacen en este capítulo:
- Los métodos predictor-corrector “sienten” la pendiente en diferentes momentos del futuro para calcular el mejor paso adelante en el tiempo.
- El método de Heun y el método de punto medio son ejemplos simples de métodos predictor-corrector. Ambos son\(O(h^2)\) métodos.
- El método del caballo de batalla utilizado para resolver una gran fracción de ODEs en el mundo es Runge-Kutta de 4to orden. Este método es lo primero que debes probar cuando te enfrentas a una nueva ODE si no tienes ningún conocimiento especial sobre las propiedades de la ODE.
- Como cabría esperar de su nombre, el error RMS de 4to orden Runge-Kutta escala como\(O(h^4)\).
- Todos los métodos mostrados en este capítulo son explícitos.
- Los cuadros carniceros se utilizan para catalogar los diferentes métodos predictor-corrector presentando sus coeficientes en forma tabular.


