1.5: Paso adaptativo
- Page ID
- 118889
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Elegir\(h\)
Hasta ahora no he dicho mucho sobre qué tamaño de paso\(h\) elegir. Por supuesto, las consideraciones de precisión y estabilidad sugieren que un tamaño de paso más pequeño suele ser mejor que uno más grande. Sin embargo, si su tamaño de paso es demasiado pequeño, entonces su programa tardará más en ejecutarse del necesario para obtener una respuesta precisa. Existe una compensación entre el tiempo de ejecución y el tamaño de paso. El tiempo de ejecución no importa mucho a la hora de ejecutar los programas de juguete utilizados para demostrar los diferentes métodos en este folleto, pero si estás haciendo un cálculo gigantesco del mundo real entonces no quieres perder el tiempo si no tienes que hacerlo. A menudo, el tiempo de ejecución de su programa es importante, si su programa está destinado a predecir el clima de mañana pero su programa tarda 48 horas en ejecutarse, entonces su programa es inútil.
Como primer paso, si sabe algo sobre su ODE, y en particular conoce la escala de tiempo en la que espera que cambie la solución, entonces elegir un tamaño de paso que se ajuste a esa escala de tiempo es fácil. Sin embargo, comúnmente no sabes mucho sobre el comportamiento de tu solución, razón por la cual la estás simulando en primer lugar. Además, su ODE podría comportarse mal: la solución puede ser suave y variar lentamente durante un período de tiempo, luego convertirse en ráfaga o variar rápidamente en un momento posterior. Debido a esto, el paso adaptativo es un método común útil para encontrar el mejor tamaño de paso para su simulación. La idea es simple:
- Da un solo paso de tamaño\(h\).
- Estima el error entre la verdadera solución y tu paso.
- Si el error es demasiado grande, entonces regresa y vuelve a intentar tu paso con un tamaño de paso más pequeño, por ejemplo\(h/2\). Luego usa este tamaño de paso para avanzar.
- Sin embargo, si el error es lo suficientemente pequeño, aumente el tamaño de paso para pasos futuros.
- Regresa al 1 y sigue pisando.
La idea es que el error incurrido en cada paso pueda permanecer por debajo de algún límite. En términos aproximados, si su solución cambia lentamente, entonces puede tomar pasos más grandes. Pero si su solución cambia rápidamente, entonces necesita tomar pasos más pequeños para mantener una buena precisión.
Por supuesto, la gran pregunta es, ¿cómo estimar el error? En el mejor de los casos, podría comparar su solución calculada con la solución verdadera, pero si ya tenía la solución verdadera, ¡no necesitaría ejecutar un solucionador de ODE en primer lugar! Como segundo mejor caso, se podría utilizar un llamado “oráculo”. En informática, un oráculo es una función o un programa que puedes preguntar si tu solución es verdadera o no. Es decir, puedes computar un paso, luego darle el resultado a un oráculo y dirá o “sí, tu solución es correcta” o “no, tu solución está equivocada”. Como pensamiento-experimento el oráculo es generalmente considerado como una “caja negra”, lo que significa que no necesariamente se sabe cómo funciona por dentro. Basta con saber simplemente que el oráculo dirá “sí” o “no” a su respuesta propuesta, y el oráculo dará un juicio exacto.
¿Qué es un buen oráculo para usar con un solucionador de ODE? Aquí hay dos posibilidades:
- Una idea simple es simplemente ejecutar cada paso dos veces: primero usar stepsize\(h\), luego dar dos pasos de stepsize\(h/2\) y comparar los resultados. En este caso, los\(h/2\) pasos pueden considerarse como una especie de oráculo ya que su respuesta es (presumiblemente) más precisa que el\(h\) paso. El problema con este esquema es que efectivamente ejecutas el solucionador dos veces, dos veces por cada paso. Esto hace que su programa funcione (al menos) el doble de tiempo que sea necesario.
- También podrías considerar dar un paso usando, digamos, adelante Euler, y luego dar el mismo paso usando, digamos, el método de Heun. La idea aquí es que dado que el delantero Euler es\(O(h)\) pero el método de Heun es\(O(h^2)\) entonces el método de Heun es un buen oráculo. Nuevamente, esto significa que pierdes un tiempo significativo recalculando tu paso. Por otro lado, en el método de Heun puedes reutilizar el paso inicial hacia adelante de Euler, para que recuperes algo de rendimiento a través de la reutilización de resultados previamente calculados.
Resulta que los solucionadores del mundo real utilizan una variante de posibilidad 2. Recordemos el método Runge-Kutta de cuarto orden de 4.6. El método RK4 presentado allí es un miembro de una familia más grande de métodos Runge-Kutta de orden variable. El famoso solucionador ode45 () de Matlab utiliza un método llamado Dormand-Prince order 4/5. En este solucionador se utilizan dos métodos Runge-Kutta. La primera es una variante Runge-Kutta de 4to orden (no la presentada en 4.6), y la segunda es un método Runge-Kutta de 5to orden. Los coeficientes utilizados para calcular los pasos intermedios de ambos métodos son los mismos, solo que el cálculo final es diferente. Por lo tanto, la cantidad de cómputos adicionales requeridos para implementar la comprobación de oráculo es una pequeña parte del cálculo general en cada paso. El cuadro combinado de Carnicero de los métodos utilizados en ode45 () se muestran en [tab:5.1]. También puedes ver estos parámetros en Matlab emitiendo el comando “dbtype 201:213 ode45", que emite la mesa Butcher en una forma ligeramente diferente a la anterior.
En cuanto a cambiar el tamaño del paso, mi ingenua sugerencia en el ítem 1 reduce o duplica el tamaño del paso dependiendo del error medido por el método. Un mejor enfoque sería afinar el tamaño del paso dependiendo de la magnitud del error observado. Es decir, hacer que el nuevo tamaño de paso dependa del error real observado en lugar de reducir a la mitad ciegamente o duplicar el paso. Existen algoritmos para hacer tal ajuste fino, pero están fuera del alcance de este folleto.
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1/5 | 1/5 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3/10 | 3/40 | 9/40 | 0 | 0 | 0 | 0 | 0 |
| 4/5 | 44/45 | -56/15 | 32/9 | 0 | 0 | 0 | 0 |
| 8/9 | 19372/6561 | -25360/2187 | 64448/6561 | -212/729 | 0 | 0 | 0 |
| 1 | 9017/3168 | -355/33 | 46732/5247 | 49/176 | -5103/18656 | 0 | 0 |
| 1 | 35/384 | 0 | 500/1113 | 125/192 | -2187/6784 | 11/84 | 0 |
| 35/384 | 0 | 500/1113 | 125/192 | -2187/6784 | 11/84 | 0 | |
| 5179/57600 | 0 | 7571/16695 | 393/640 | -92097/339200 | 187/2100 | 1/40 |
Ejemplo: la ecuación logística
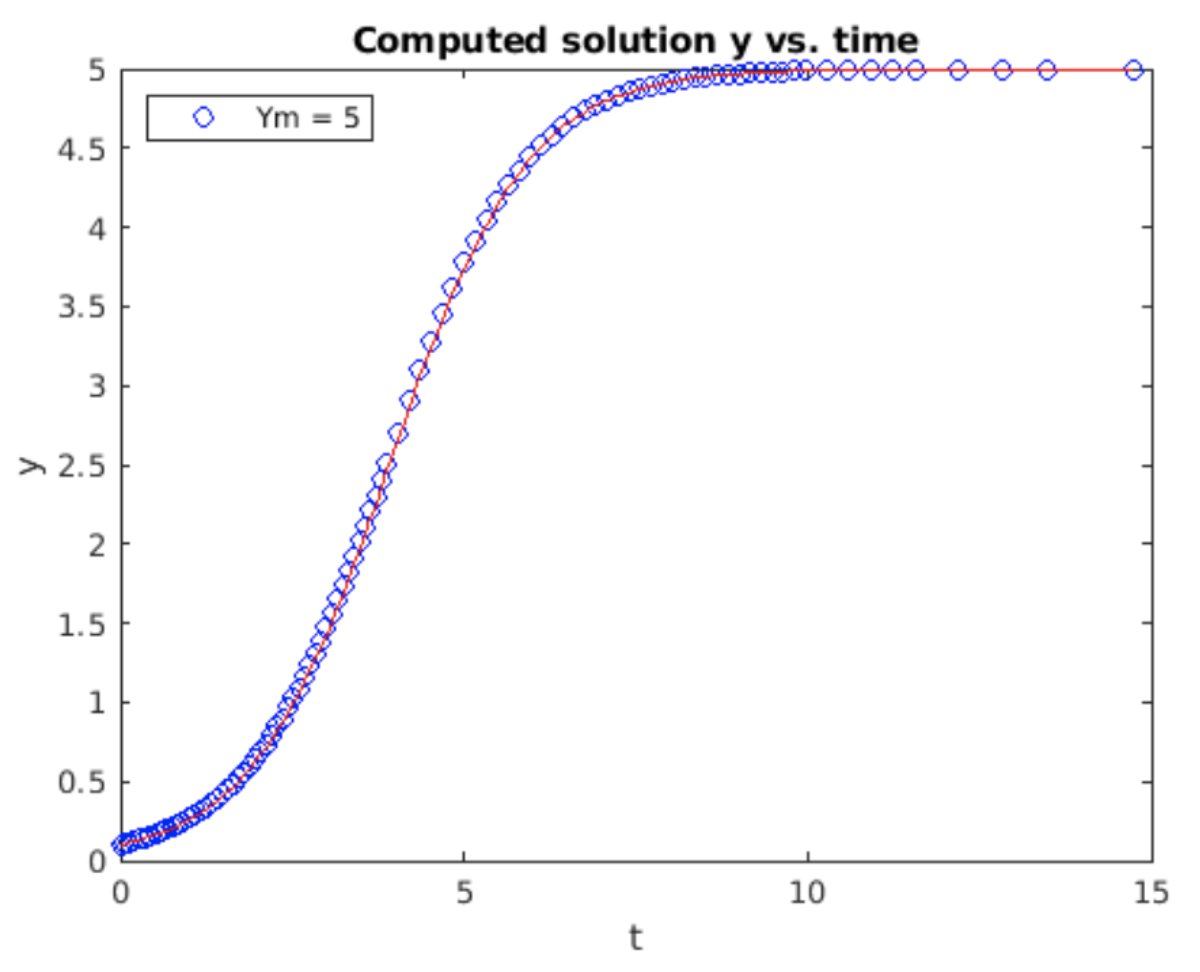
En lugar de demostrar el completo Dormand-Prince 4/5, mostraré un paso a paso adaptativo más simple basado en la posibilidad 2 anterior. El algoritmo del programa se muestra en [alg:6]. Utilizo la ecuación logística como ejemplo porque la solución tiene (aproximadamente) dos regiones de interés: Una fase de crecimiento exponencial que varía rápidamente al inicio de la carrera seguida de una meseta como\(t \rightarrow \infty\). Los resultados obtenidos de la implementación del programa de Matlab se muestran en 5.1. El tamaño del paso claramente permanece pequeño durante el inicio de la ejecución, pero cuando la solución se estabiliza (no cambia) el tamaño del paso aumenta. Esto es particularmente evidente para los tiempos\(t > 10\).
__________________________________________________________________________________________________________________________________________________
Algoritmo 6 Método paso adaptativo ingenuo
__________________________________________________________________________________________________________________________________________________
Entradas: condición inicial\(y_0 = [u_0, v_0]^T\), tiempo de finalización\(t_{end}\).
Inicializar:\(t_0 = 0, y_0, h\).
Inicializar:\(tol_1 = 1e - 2, tol_2 = 2e-4\).
para\(n=0: t_{end}/h\) hacer
Obtener pendiente inital:\(s_1 = f(t_n, y_n)\)
Avanza el paso de Euler:\(y_{fe} = y_n + h s_1\)
Obtener pendiente en una nueva posición:\(s_2 = f(t_n, y_{fe})\)
Toma el paso de Heun:\(y_h = y_n + h (s_1+s_2)/2\)
Compruebe la diferencia entre los pasos de Euler y Heun:\(\delta = ||y_{fe}-y_h||\)
si\(\delta > tol_1\) then
Error demasiado grande - paso de disminución:\(h=h/2\)
de lo contrario si\(\delta < tol_2\) entonces
Error muy pequeño - aumentar el paso:\(h=2h\)
else
Error ni demasiado pequeño ni demasiado grande. Mantenga el paso.
terminar si
fin para
retorno\(y_n\).
ODEs rígidas
En la última sección vimos un método de paso adaptativo que dio pequeños pasos cuando la solución varió rápidamente, y dio pasos más grandes cuando la solución varió lentamente. El concepto de variación lenta vs. rápida se generaliza al concepto de “rigidez” de una ODE. Una definición exacta del término “rígido” es difícil de precisar, pero la intuición básica es que una ODE rígida es aquella en la que hay que dar pequeños pasos en algunos momentos para mantener la precisión, pero puede dar pasos mucho más grandes en otras ocasiones. El problema con una ODE rígida es que si usas un paso de tiempo fijo\(h\), entonces necesitas\(h\) ser muy pequeño para aquellas secciones de la ODE que requieren pasos pequeños. Sin embargo, el paso a paso luego avanza lentamente sobre secciones donde podría usar un paso grande\(h\) y rápidamente, ¡lo que significa que está perdiendo el tiempo de computación! Hacer frente a la rigidez es por lo que los solucionadores adaptativos son tan importantes.
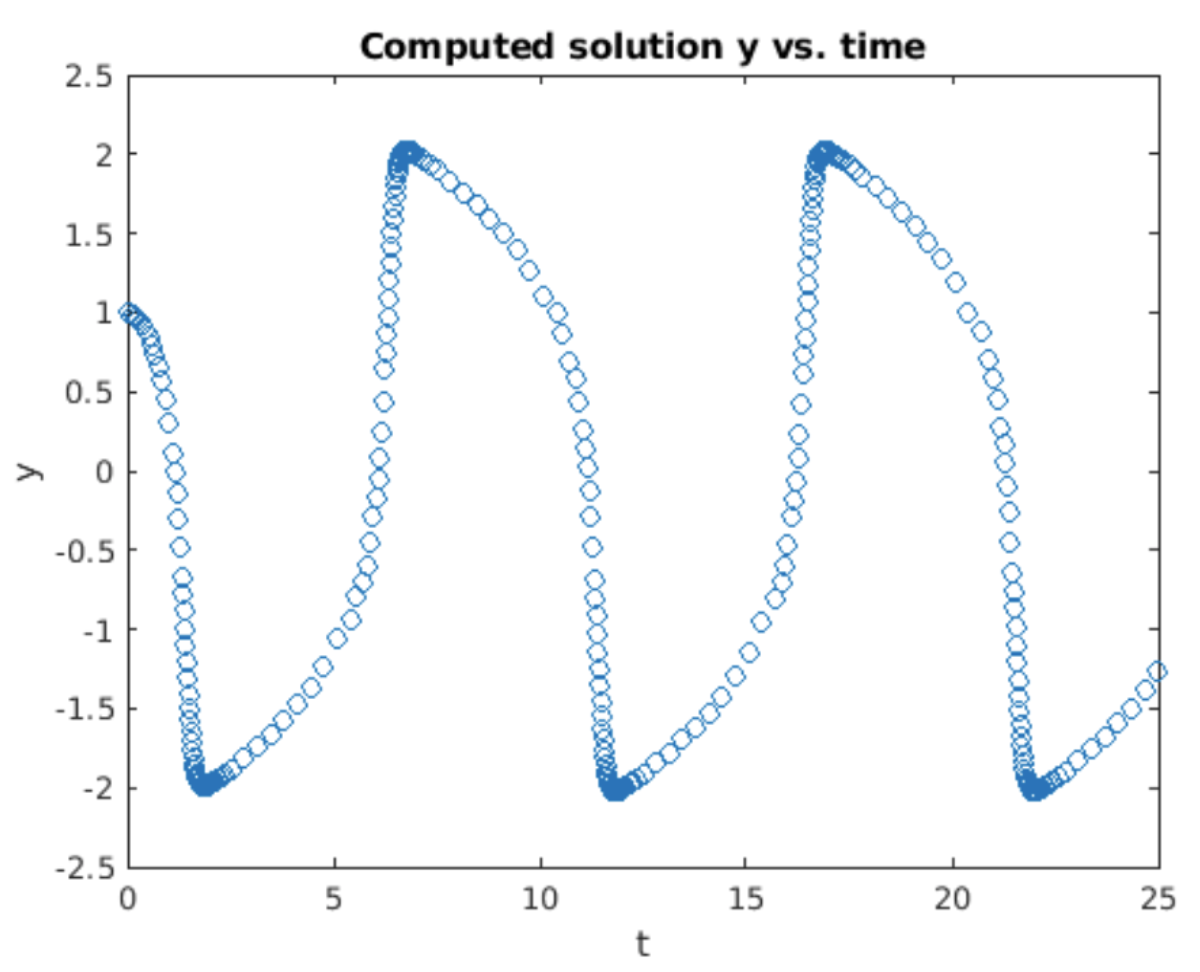
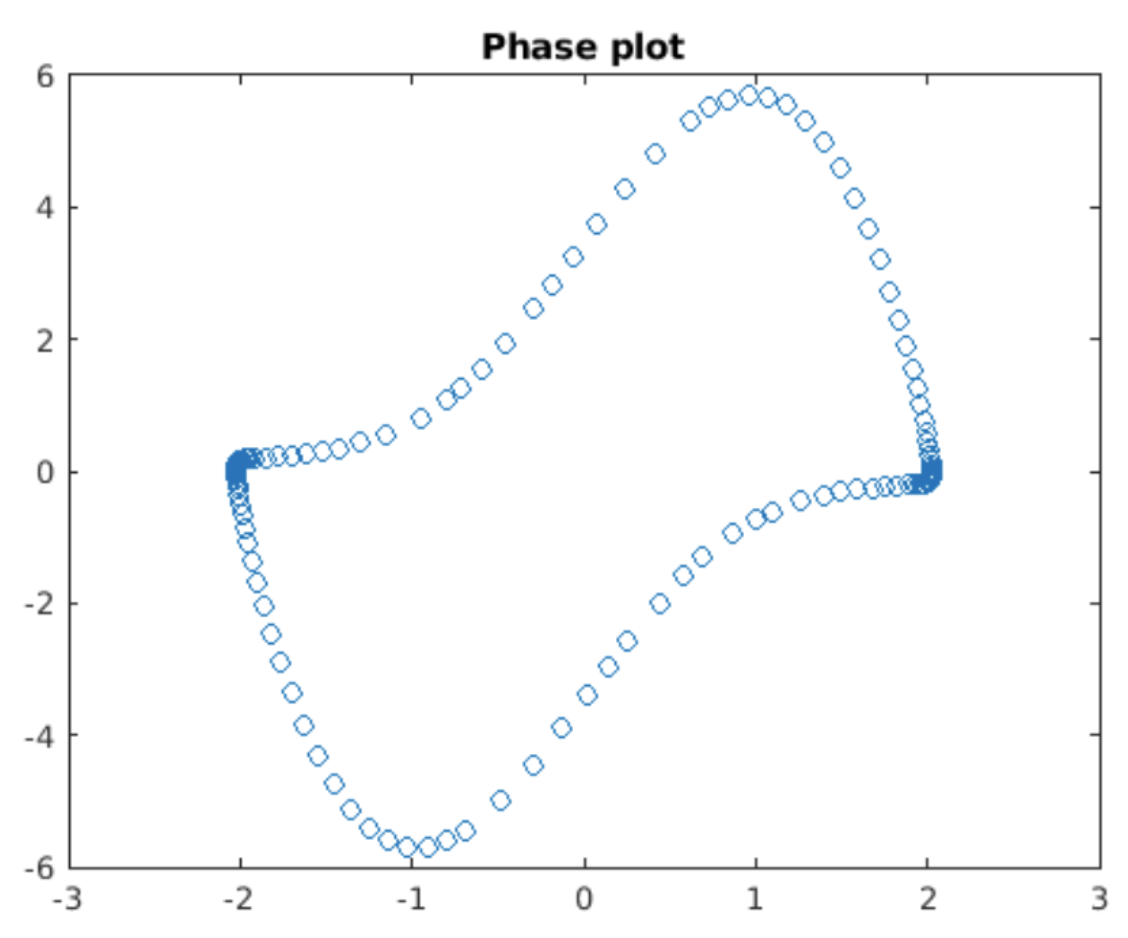
La ecuación de Van der Pol es un ejemplo común de una ODE rígida. La solución calculada usando el paso a paso adaptativo se muestra en 5.2. Cuando la solución alcanza su punto máximo alrededor\(y \approx \pm 2\) del paso, el tamaño debe disminuir significativamente para mantener una solución precisa. La inspección de la gráfica de fase 5.3 muestra otra visión de este fenómeno: cuando la solución da un giro duro a la derecha, el tamaño del paso debe disminuir para seguir la solución, pero el tamaño del paso puede aumentar cuando la solución se aleja del “giro a la derecha”. La pregunta es, ¿por qué el tamaño del paso necesita disminuir en estos puntos?
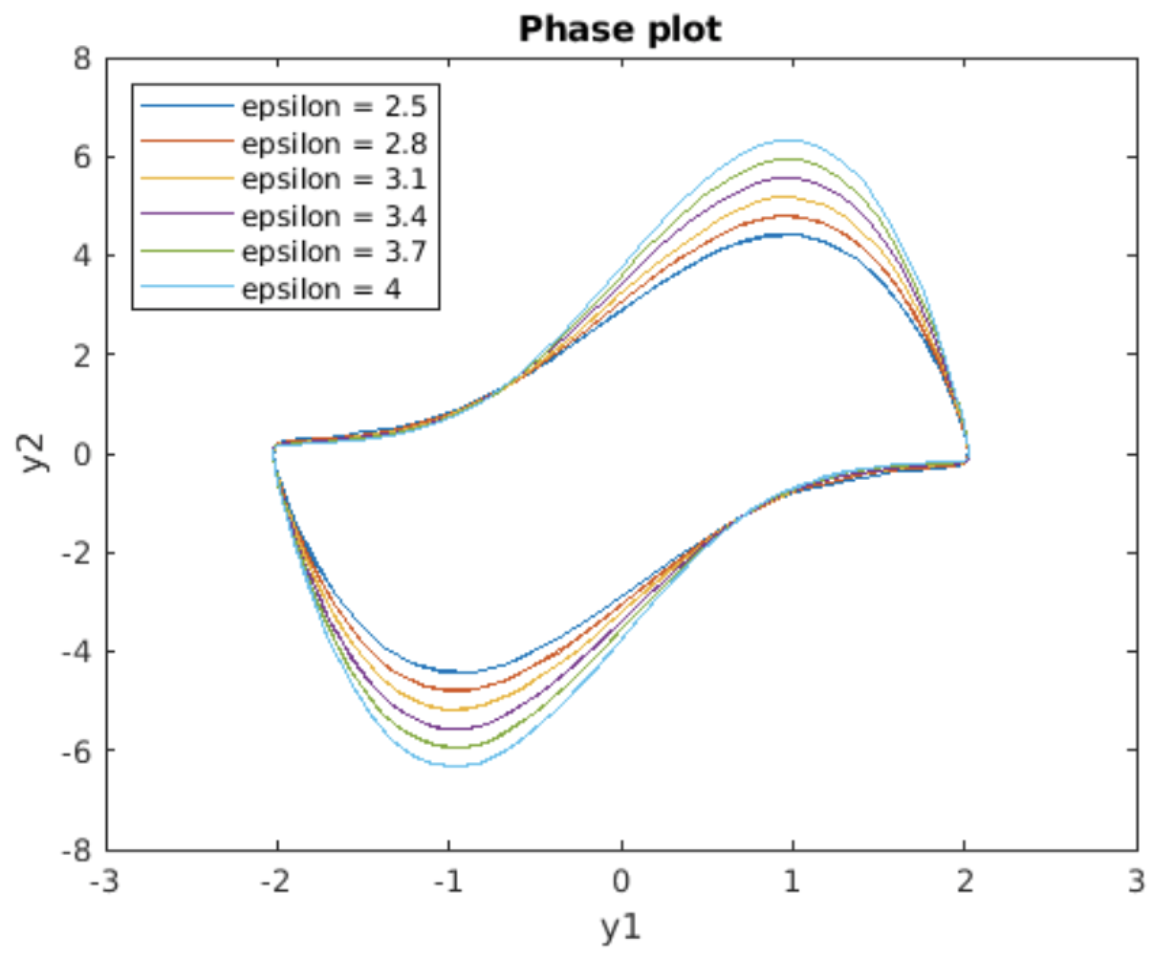
en el plano de fase, pero no en otros? La respuesta viene de considerar toda la familia de soluciones a la ecuación de Van der Pol en el plano de fase. Se muestra una gráfica de la situación en 5.4, que es una gráfica de fase para valores variables de\(\epsilon\). Las soluciones para variar\(\epsilon\) se agrupan en las esquinas, pero se extienden lejos de esas regiones. Cerca de las esquinas, permanecer en la solución correcta (es decir, no saltar a otra solución de la familia) depende muy sensiblemente de seguir de cerca la trayectoria de solución correcta. El paso a paso adaptativo de alguna manera “siente” esta sensibilidad y
en consecuencia ajusta el tamaño del paso para permanecer en la trayectoria correcta. La importancia de los solucionadores adaptables de tamaño de paso es simplemente que si el solucionador no cambia su tamaño de paso, entonces para obtener una solución precisa necesitaría usar un paso muy pequeño\(h\) para permanecer en la trayectoria correcta en las regiones sensibles. Las regiones sensibles son aquellas en las que la familia de soluciones se encuentra cerca una de la otra. Sin embargo, pequeño\(h\) significa que el tiempo de ejecución del solucionador sería mucho más largo de lo necesario ya que también daría pequeños pasos a través de la región donde la trayectoria de la solución es relativamente insensible. El solucionador adaptativo es el mejor de ambos casos: paso rápido a través de las regiones insensibles y paso lento y cuidadoso a través de las regiones sensibles.
Resumen del capítulo
Estos son los puntos importantes que se hacen en este capítulo:
- Un método de tamaño de paso adaptativo cambia el tamaño del paso\(h\) para mantener el error de solución permanece por debajo de cierta tolerancia. Cuando el paso a paso detecta que el error de solución está creciendo, disminuirá el tamaño del paso hasta que el error resultante de un paso permanezca por debajo de la tolerancia. Cuando el paso a paso detecta que el error de solución es lo suficientemente pequeño, aumentará el tamaño del paso para acelerar la solución.
- Un sistema rígido es aquel en el que la solución evidencia regiones de rápida y regiones de variación lenta, o más exactamente alta o baja sensibilidad a soluciones adyacentes a la ODE.