1.6: Métodos lineales multipaso

La forma canónica de una ODE de primer orden se da en [eq:6.1]. Hasta ahora, los algoritmos del solucionador de ODE que hemos examinado comenzaron a partir de aproximar el operador derivado en [eq:6.1], luego construyendo sobre esa aproximación para crear un solucionador. \[\tag{eq:6.1} \frac{dy}{dt} = f(t, y)\]Ahora intentaremos un enfoque diferente. En lugar de partir de la derivada, piense en cómo podríamos construir un solucionador de ODE integrando ambos lados de [eq:6.1] y luego creando un método de paso a paso. Específicamente, considere la ecuación\[\tag{eq:6.2} y_{n+1} = \int_{t_n}^{t_{n+1}} f(t, y(t)) dt + y_n\] Esta ecuación se deriva de [eq:6.1] por integración. El problema de hacer la integración directamente es que el RHS requiere conocimiento de\(y(t)\) — ¡lo que estamos tratando de encontrar! Pero, ¿qué pasa si elegimos una aproximación para\(f\) y hacemos la integración? Resulta que se crean diferentes métodos multipaso mediante el uso de diferentes aproximaciones para\(f\). Vamos a ver algunos métodos en este capítulo.

Trapezoidal

Una simple aproximación a\(f\) in [eq:6.2] es asumir que los puntos\((t_n, f_n)\) y\((t_{n+1}, f_{n+1})\) están conectados a través de una línea recta. Este es el caso de la interpolación lineal entre dos puntos y se muestra en 6.1. Interpolación lineal entre\(t_n\) y\(t_{n+1}\) puede escribirse de esta forma:\[\tag{eq:6.3} f(t) = (1-\alpha) f_n + \alpha f_{n+1}\] donde\(\alpha \in [0, 1]\). Obviamente, cuando\(\alpha = 0\) lleguemos\(f(t) = f_n\) y cuando\(\alpha = 1\) lleguemos\(f(t) = f_{n+1}\). Dado que [eq:6.3] es lineal en\(\alpha\), esta expresión dibuja una línea recta entre estos dos puntos.

Ahora considere lo que sucede si usamos el método de interpolación [eq:6.3] en la integral [eq:6.2]. Para facilitar el álgebra reconocemos\(\alpha = (t - t_n)/h\) así que\(h d\alpha = dt\).

Figura 6.1: El método trapezoidal. La línea punteada roja es la interpolación lineal. La región gris corresponde al “área bajo la curva” que es calculada por la integral [EQ:IntegrateLinearInterp]. Tenga en cuenta que este método es implícito.

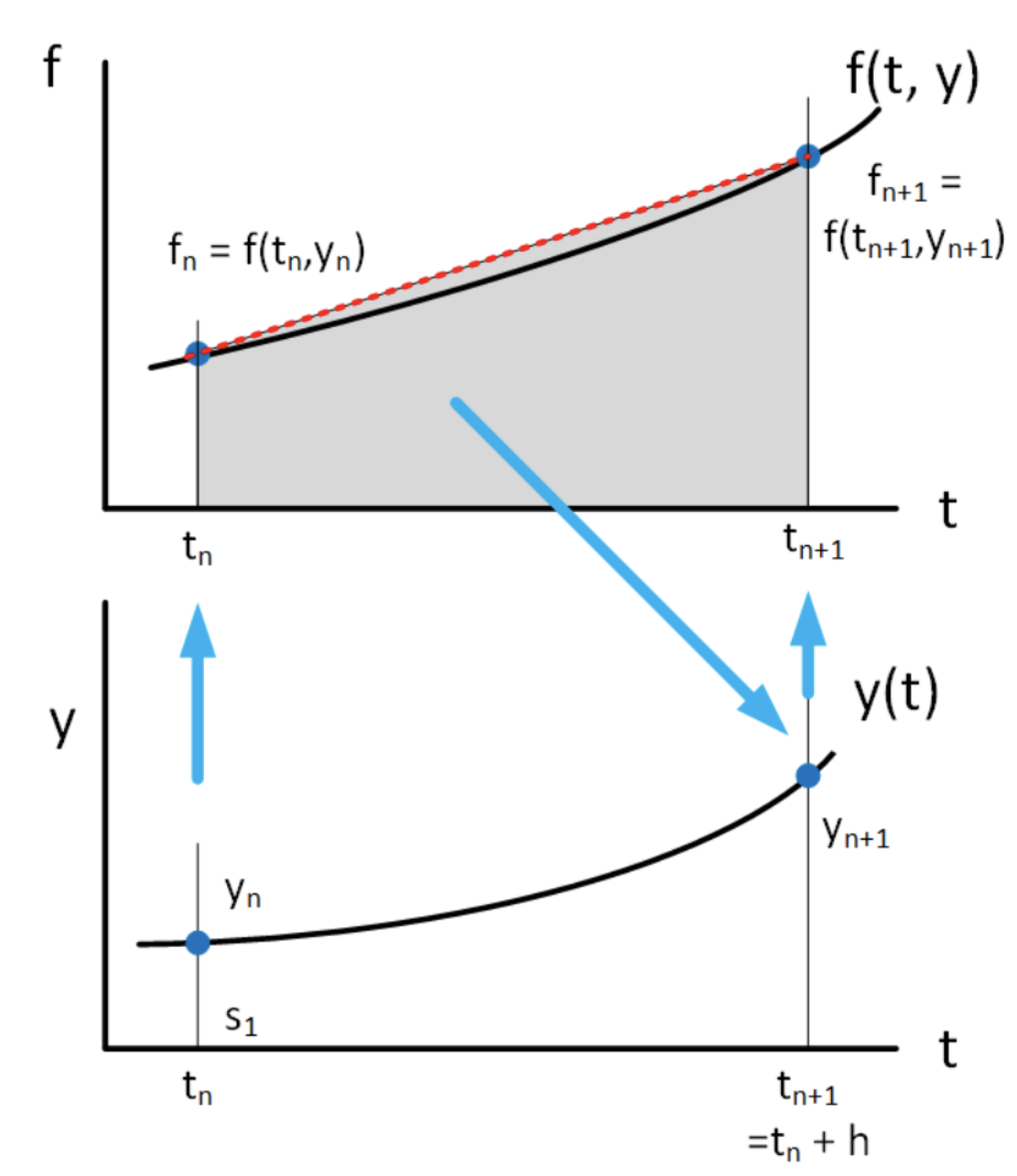
En este caso, [eq:6.2] se convierte en\[\tag{eq:6.4} y_{n+1} = h \int_{0}^{1} \left( (1-\alpha) f_n + \alpha f_{n+1} \right) d \alpha + y_n\] que se integra a\[\tag{eq:6.5} y_{n+1} = \frac{h}{2} \left( f_{n+1} + f_n \right) + y_n\] Esta es una iteración que nos lleva de\(t_n\) a\(t_{n+1}\). Aquí hay algunas cosas a tener en cuenta sobre [eq:6.5]:

• Este es un método implícito — para entrar\(y_{n+1}\) en el LHS es necesario saber de\(f_{n+1}\) cuál depende\(y_{n+1}\). Afortunadamente, ya sabemos cómo lidiar con métodos implícitos —usar un rootfinder como el método de Newton.
• La ecuación cuya raíz encontrar es\(g(y_{n+1}) = y_{n+1} -\frac{h}{2} \left( f_{n+1} + f_n \right) - y_n = 0\) dónde\(f_{n+1} = f(t_{n+1}, y(t_{n+1}))\) y\(f_{n} = f(t_{n}, y(t_{n}))\) como de costumbre.
• Este método se ha aproximado\(f(t)\) utilizando una línea recta entre los dos puntos finales, para luego integrar la aproximación. Esto es exactamente lo mismo que el “método trapezoidal” para la integración numérica que puede haber visto en una clase de análisis numérico anterior. Por lo tanto, a este solucionador de ODE se le llama el “método trapezoidal”.

Ejemplo: la ODE de crecimiento exponencial

Figura 6.2: La ODE de crecimiento exponencial integrada mediante el método trapezoidal. Los círculos abiertos son los resultados calculados, las líneas son la solución analítica. El ajuste es bastante bueno, al menos en esta escala.

Figura 6.3: Escalado de error del método trapezoidal. El error se escala como\(O(h^2)\).

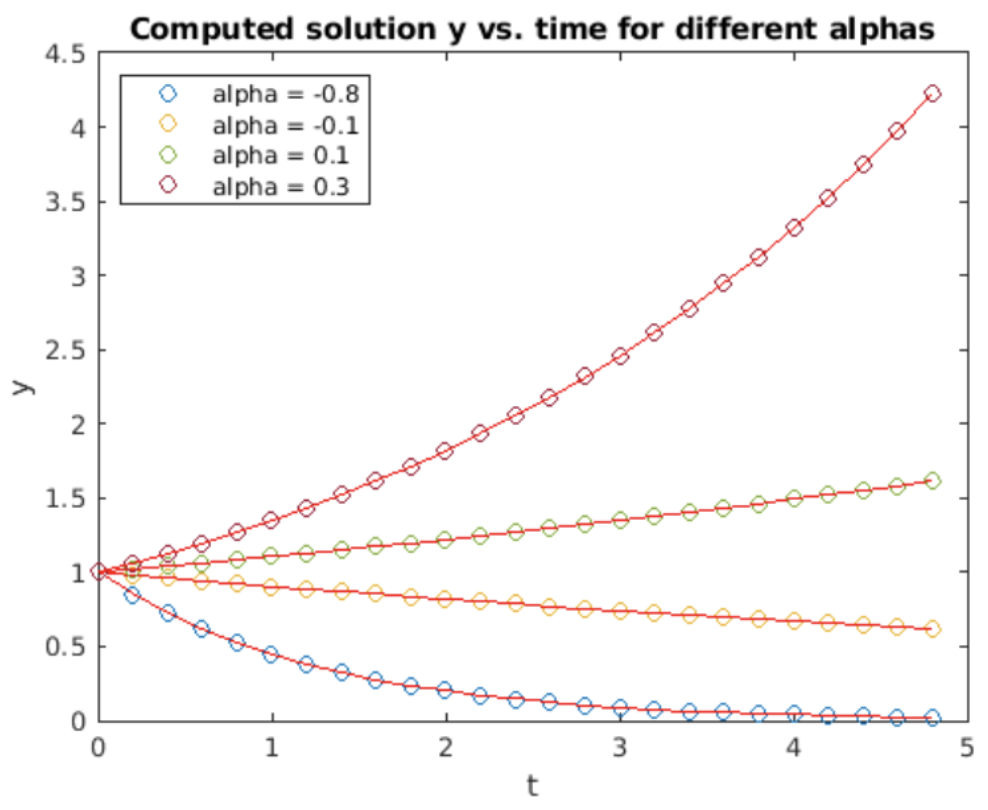
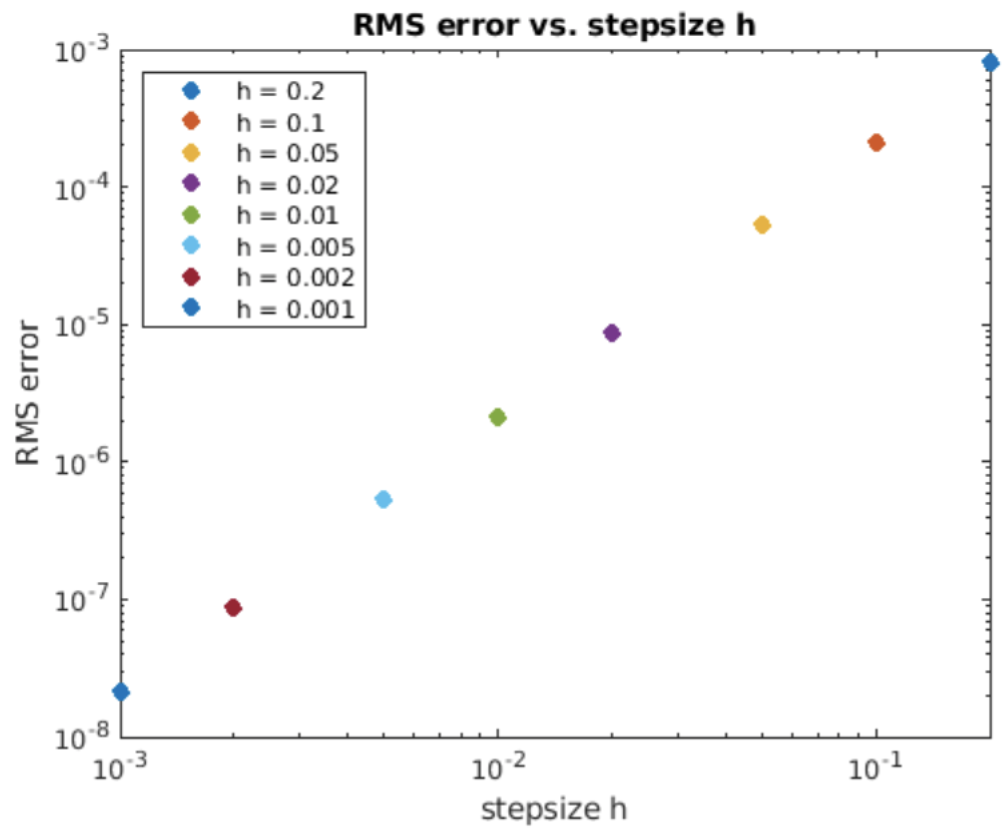
Método Adams-Bashforth — 2do orden

El método trapezoidal utiliza interpolación lineal entre puntos en\(t_n\) y\(t_{n+1}\). Se trata de un método implícito, es decir, que supone que conocemos el valor\(y_{n+1}\) final para poder calcular el paso usando\(f_{n+1} = f(t_{n+1}, y_{n+1})\). Sin embargo, el cálculo de pasos es lo que se utiliza para obtener el valor final\(y_{n+1}\). Por lo tanto, calcular el paso requiere de una operación de resolución de la que desenredar\(y_{n+1}\)\(f_{n+1}\). Una operación de resolución es generalmente costosa: los solucionadores como el método de Newton son iterativos y uno podría necesitar varias iteraciones antes de encontrar la solución. ¿No sería mejor usar de alguna manera la interpolación lineal para crear un método explícito que no requiera un paso de solucionador?

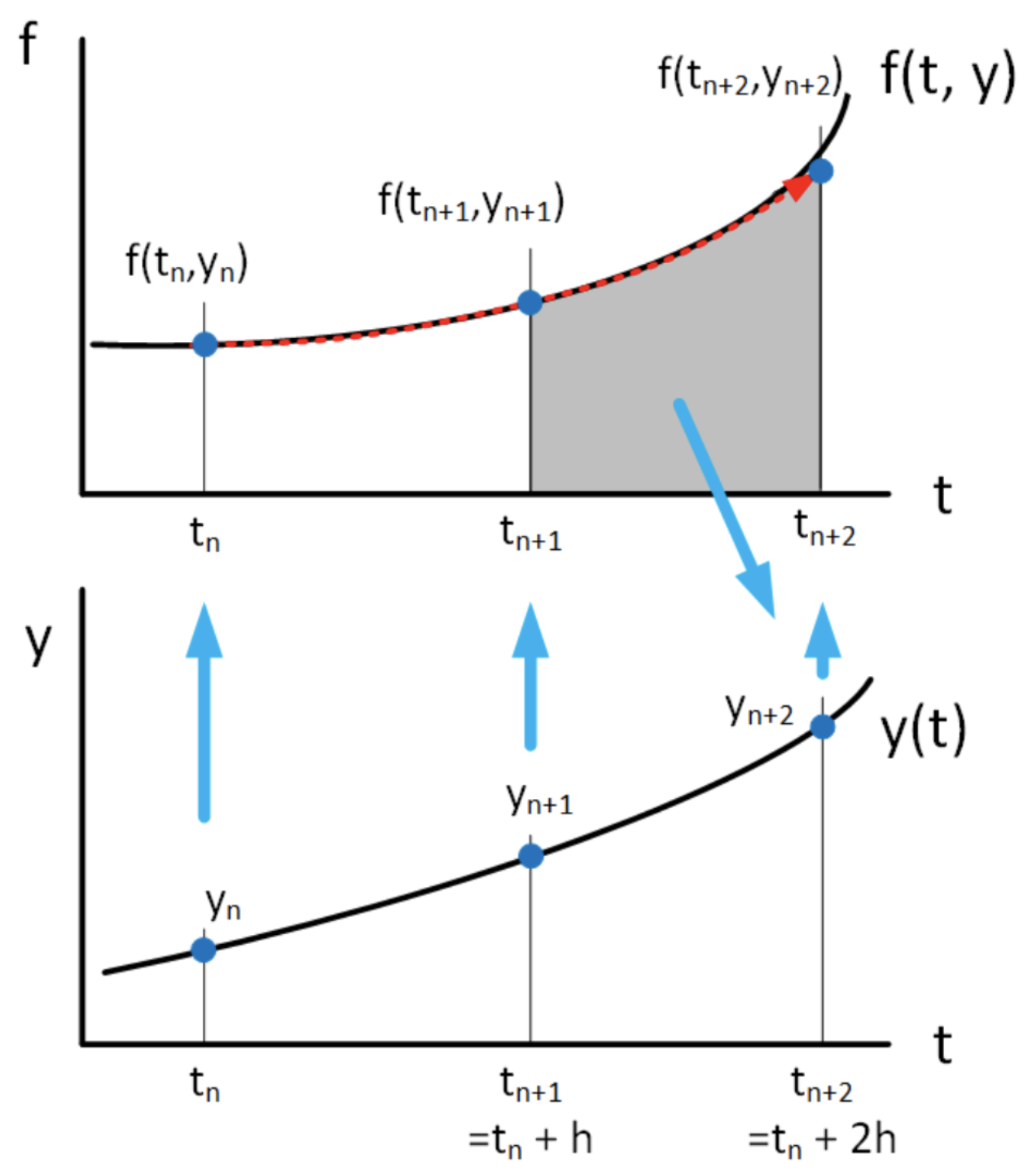
El método explícito Adams-Bashforth de 2do orden es tal método. Utiliza los valores conocidos (previamente calculados) a veces\(t_n\) y\(t_{n+1}\) para calcular el valor en\(t_{n+2}\). La idea se muestra en 6.4. En cierto sentido, Adams-Bashforth toma la fórmula de interpolación [eq:6.3] definida en\(t \in [t_n, t_{n+1}]\) y

Figura 6.4: El método Adams-Bashforth de 2do orden. Primero, se realiza interpolación lineal entre los puntos\((t_n, y_n)\) y\((t_{n+1}, y_{n+1})\). Luego la línea se extiende hasta\(t_{n+2}\) y la región gris bajo la curva se integra por [eq:6.7] para dar el nuevo valor\(y_{n+2}\).

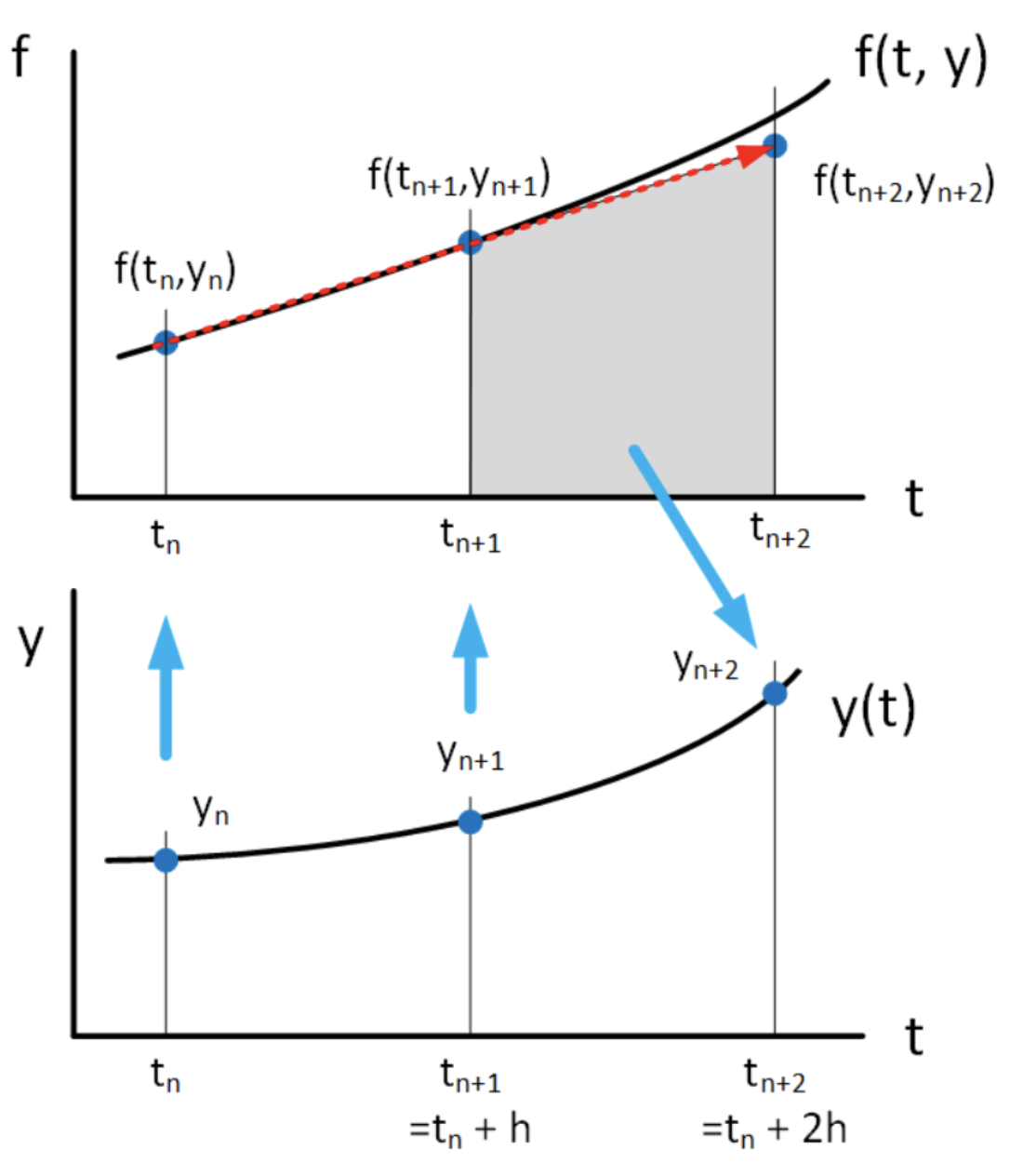
lo extrapola hacia adelante al tiempo\(t_n+2\). Es decir, computa la integral

\[\tag{eq:6.6} y_{n+2} = \int_{t_{n+1}}^{t_{n+2}} f_{n, n+1}(t, y(t)) dt + y_{n+1}\]usando la aproximación a\(f_{n, n+1}\) basada en la fórmula de interpolación lineal definida en\(t \in [t_n, t_{n+1}]\), [eq:6.3]. Transformamos la integral [eq:6.6] a través del cambio habitual de variables\(\alpha = (t - t_n)/h\) para obtener\[\tag{eq:6.7} y_{n+2} = h \int_{1}^{2} \left( (1-\alpha) f_n + \alpha f_{n+1} \right) d \alpha + y_{n+1}\] Tras la integración obtenemos el método Adams-Bashforth de segundo orden,

\[\tag{eq:6.8} y_{n+2} = h \left( \frac{3}{2} f_{n+1} - \frac{1}{2} f_{n} \right) + y_{n+1}\]

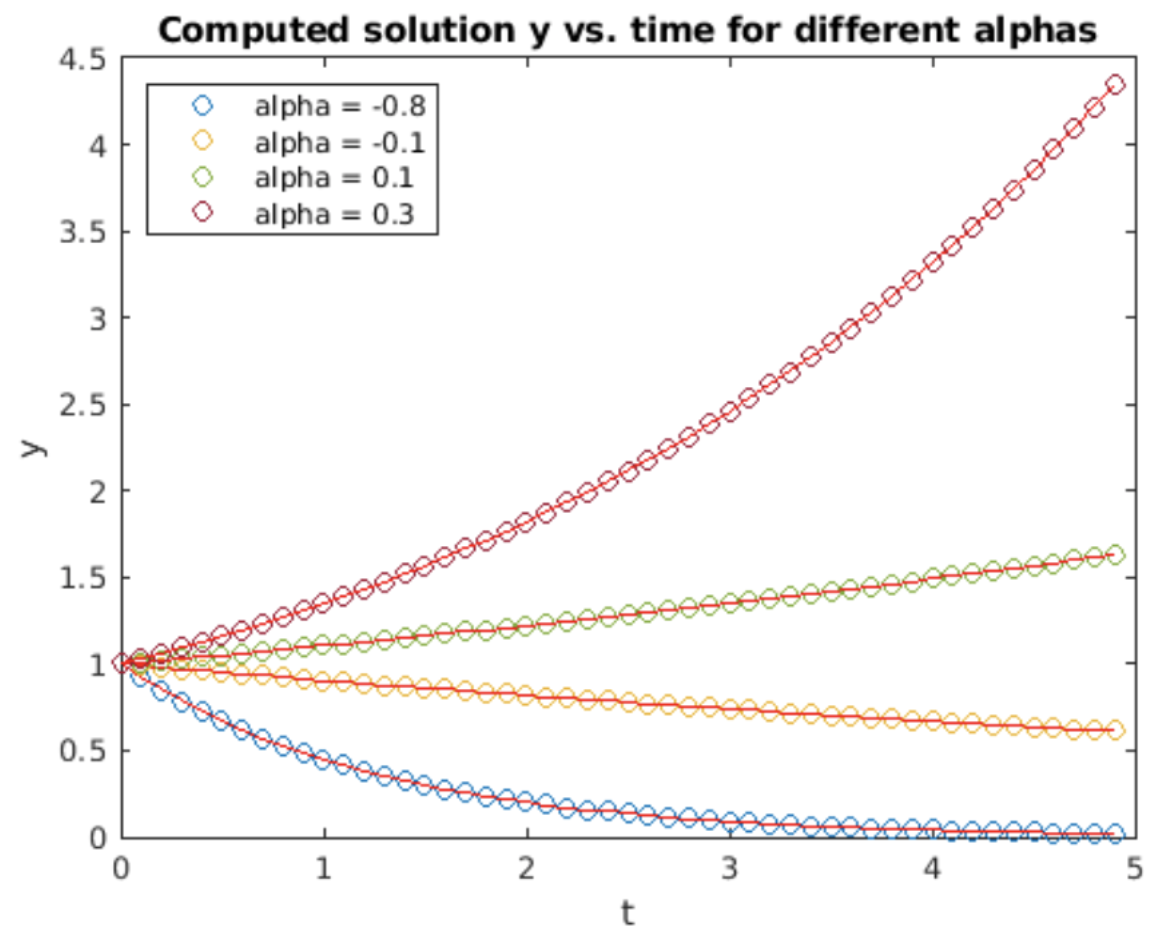
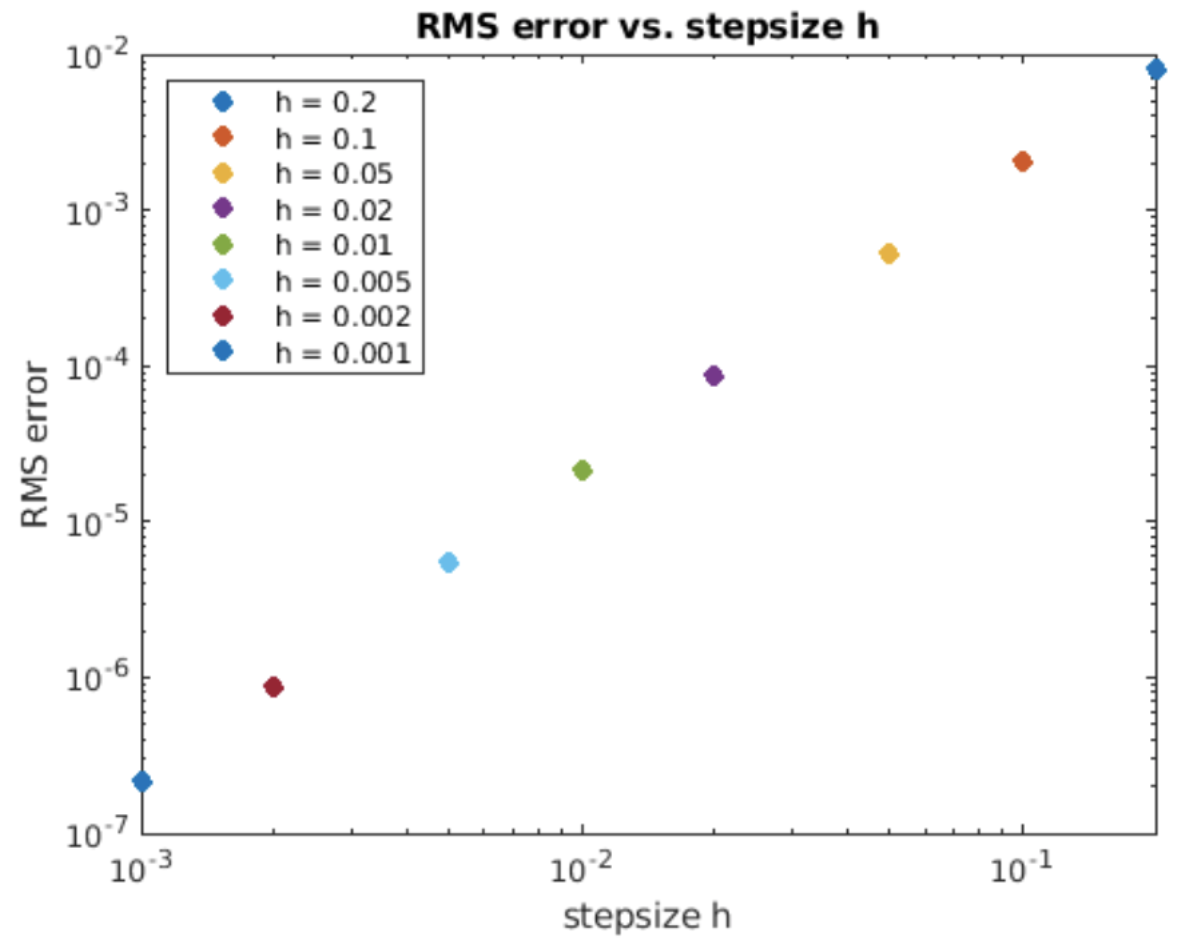
Observe que Adams-Bashforth de segundo orden utiliza dos muestras de la función en\(t_n\) y\(t_{n+1}\) para calcular el valor futuro en\(t_{n+2}\). Este es un método explícito ya que presumiblemente ya sabemos\(f_{n+1}\) y a la\(f_n\) hora de computar\(f_{n+2}\). Pero esto plantea la pregunta, ¿cómo iniciar esta iteración? Es decir, solo tenemos una condición inicial\(y_0\), pero necesitamos dos\(y\) valores para iterar. La respuesta es que uno puede comenzar con\(y_0\), luego usar un solo paso de, por ejemplo, avanzar Euler o Runge-Kutta para obtener\(y_1\), luego continuar la solución usando Adams-Bashforth. Este es el método empleado en el programa Matlab cuya salida se muestra en 6.5. Tenga en cuenta que la precisión es\(O(h^2)\), como se esperaba de un método de segundo orden.

Figura 6.5: La ODE de crecimiento exponencial integrada usando Adams-Bashforth de 2do orden.

Figura 6.6: Escalado de error de Adams-Bashforth de 2do orden. El error se escala como\(O(h^2)\).

Método Adams-Bashforth — 3er orden

El método Adams-Bashforth de segundo orden utilizó interpolación lineal para aproximar la función a\(f(t,y)\) lo largo del intervalo\(t_n \le t \le t_{n+1}\), luego usó esa aproximación en la integral [eq:6.2] para encontrar\(y_{n+1}\). ¿Y si quieres más precisión? ¿Se puede utilizar la interpolación cuadrática en tres puntos pasados para encontrar el valor futuro? La respuesta es “sí”, y la ventaja de esto es que el orden del método aumenta. En esta sección derivaremos el método Adams-Bashforth de tercer orden (interpolación cuadrática).

Dados dos puntos\((t_n, y_n)\) y\((t_{n+1}, y_{n+1})\) podemos trazar una línea recta a través de ellos. Dados tres puntos, podemos dibujar una cuadrática (una parábola) a través de ellos. Este es el proceso de interpolación que probablemente hayas estudiado en una clase de matemáticas anterior. Dado un conjunto de puntos, hay varias formas de escribir un polinomio interpolante que pasa a través de ellos. En este caso, se nos dan tres puntos,\((t_n, y_n)\)\((t_{n+1}, y_{n+1})\), y\((t_{n+2}, y_{n+2})\), y usaremos el polinomio de interpolación Lagrange para anotar la cuadrática. Es\[\begin{gathered} \label{eq:LagrangeInterpolation} \nonumber f(t) = \frac{(t-t_{n+1})(t-t_{n+2})}{(t_{n}-t_{n+1})(t_{n}-t_{n+2})} f_{n} +\frac{(t-t_{n})(t-t_{n+2})}{(t_{n+1}-t_{n})(t_{n+1}-t_{n+2})} f_{n+1} \\ \nonumber +\frac{(t-t_{n})(t-t_{n+1})}{(t_{n+2}-t_{n})(t_{n+2}-t_{n+1})} f_{n+2}\end{gathered}\]\[\label{eq:LagrangeInterpolation1} \nonumber = \frac{(t-t_{n+1})(t-t_{n+2})}{2 h^2} f_{n} +\frac{(t-t_{n})(t-t_{n+2})}{-h^2} f_{n+1} +\frac{(t-t_{n})(t-t_{n+1})}{2 h^2} f_{n+2}\] Esta expresión puede parecer desagradable, pero tenga en cuenta que es sólo un cuadrático: Cada término es de segundo orden en\(t\). Ahora insertamos esta expresión en la integral [eq:6.2] para encontrar\(y_{n+3}\):\[\nonumber y_{n+3} = \int_{t_{n+2}}^{t_{n+3}} \frac{(t-t_{n+1})(t-t_{n+2})}{2 h^2} f_{n} +\frac{(t-t_{n})(t-t_{n+2})}{-h^2} f_{n+1} +\frac{(t-t_{n})(t-t_{n+1})}{2 h^2} f_{n+2} dt + y_n\] Lo que hay que tener en cuenta es que usamos puntos anteriores\((t_{n}, y_{n})\),\((t_{n+1}, y_{n+1})\),\((t_{n+2}, y_{n+2})\) para crear una versión aproximada de\(f(t, y)\) usando interpolación. Entonces integramos esa aproximación a lo largo del intervalo\(t \in [t_{n+2}, t_{n+3}]\) para obtener\(y_{n+3}\). El método se muestra esquemáticamente en 6.7.

Figura 6.7: El método Adams-Bashforth de tercer orden. Las flechas azules apuntando hacia arriba indican que los tres puntos\(f_n\),\(f_{n+1}\) y\(f_{n+2}\) son conocidos y se utilizan para crear el polinomio de interpolación cuadrática para\(f(t,y)\) (línea punteada roja). Ese polinomio se integra de\(t_{n+2}\)\(t_{n+3}\) a para obtener el nuevo\(y\) valor,\(y_3\).

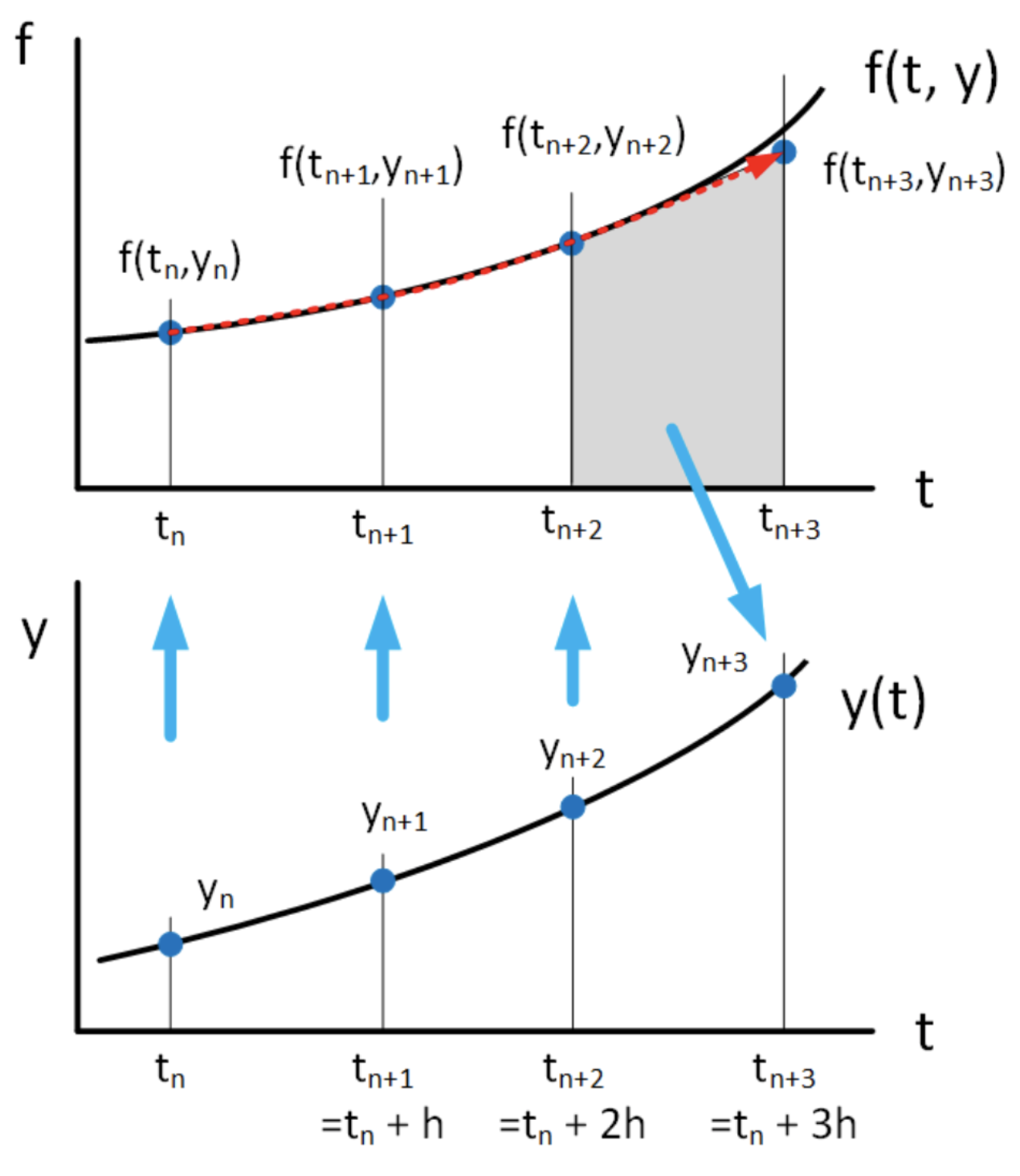
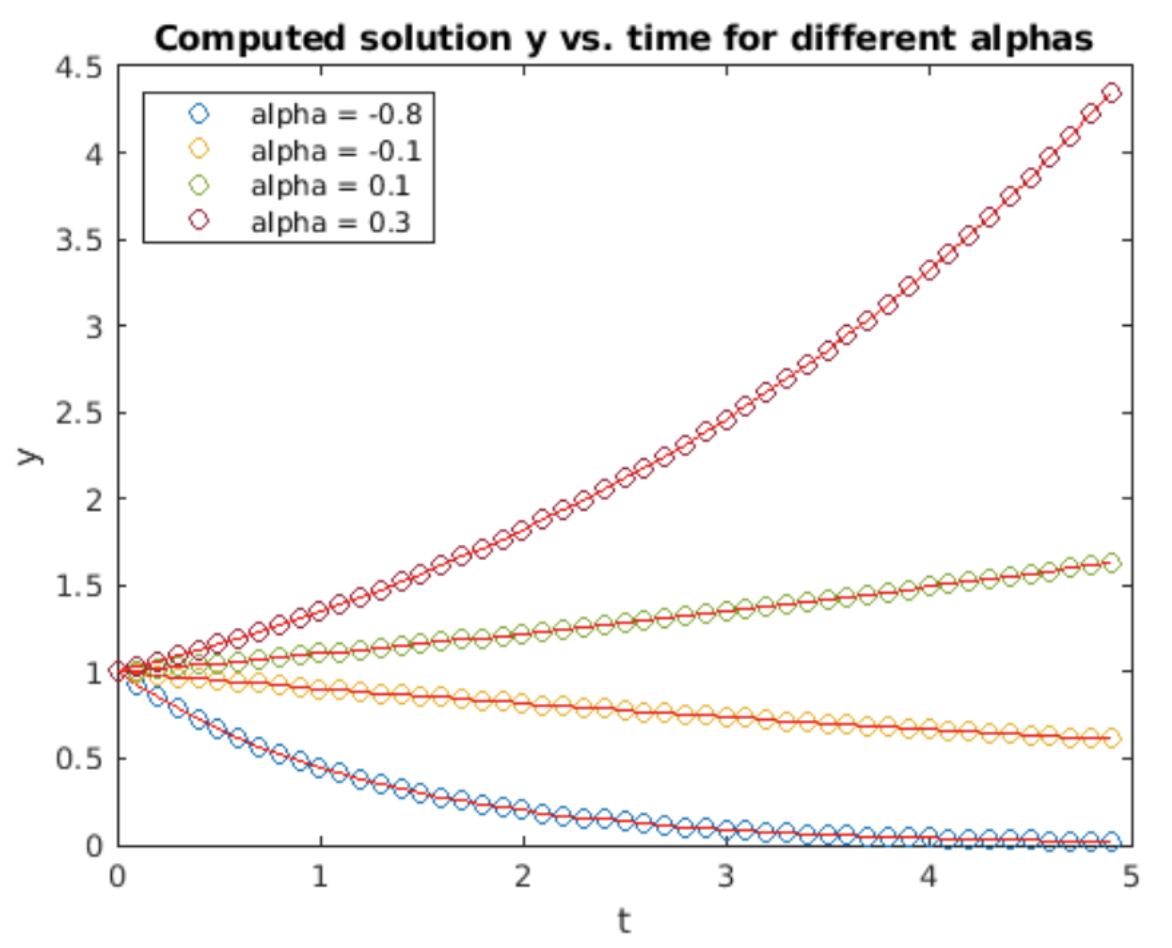
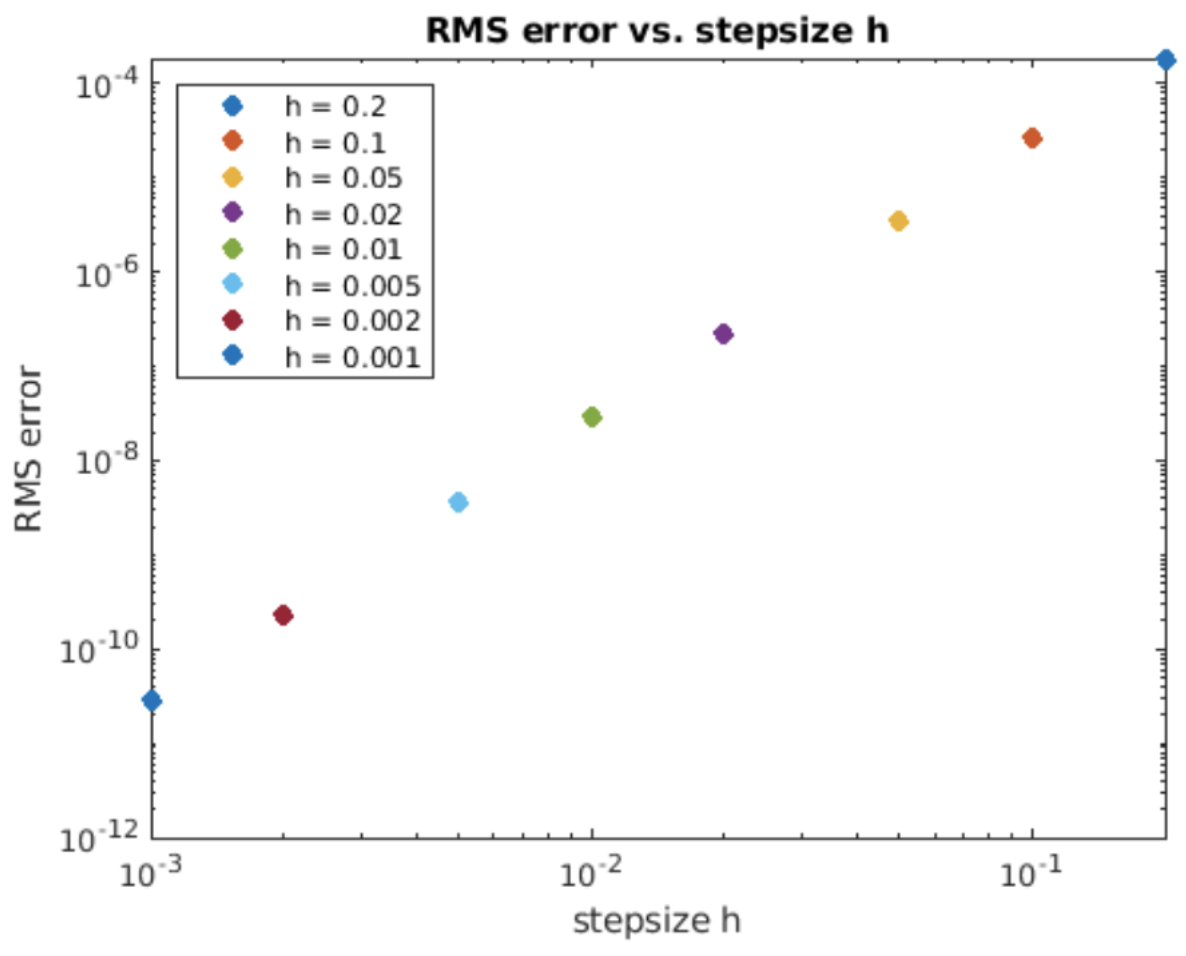
Podríamos llevar a cabo la integración de inmediato, pero sería bastante desordenada. Por lo tanto, empleamos el cambio habitual de variables\(\alpha = (t - t_{n+1})/h\). Tenga en cuenta que\(h d\alpha = dt\), y que hemos mapeado\(t = t_{n} \rightarrow \alpha = -1\),\(t = t_{n+1} \rightarrow \alpha = 0\),\(t = t_{n+2} \rightarrow \alpha = 1\), y\(t = t_{n+3} \rightarrow \alpha = 2\). Por lo tanto, la integral se convierte\[\nonumber y_{n+3} = h \int_{1}^{2} \frac{1}{2} \alpha(\alpha-1) f_{n} -(\alpha+1)(\alpha-1) f_{n+1} +\frac{1}{2} (\alpha+1)\alpha f_{n+2} d\alpha + y_n\] o\[\tag{eq:6.9} y_{n+3} = h \left( \frac{5}{12} f_{n} -\frac{4}{3} f_{n+1} +\frac{23}{12} f_{n+2} \right) + y_{n+2}\] es el método Adams-Bashforth de tercer orden. Como es de esperar para un método de tercer orden, la precisión es el orden\(O(h^3)\). Las gráficas de su solución a la ODE de crecimiento exponencial y la escala de errores se muestran en 6.8 y 6.9.

Figura 6.8: La ODE de crecimiento exponencial integrada usando Adams-Bashforth de 3er orden.

Figura 6.9: Escalado de error de Adams-Bashforth de 3er orden. El error se escala como\(O(h^3)\).

Método Adams-Moulton — 3nd orden

Los métodos de Adams-Bashforth son explícitos: utilizan el valor de\(y\) en el presente y en el pasado para calcular un paso hacia el futuro. Los métodos multipaso también pueden estar implícitos: el método trapezoidal es un ejemplo de un método multipaso implícito que ya ha visto anteriormente. También existen métodos multipaso implícitos de orden superior. Una clase son los métodos Adams-Molulton. Al igual que Adams-Bashforth, utilizan la interpolación para ajustar un polinomio a los\(f(t,y)\) valores anteriores, pero los métodos de Adams-Moulton también\(y\) incorporan el futuro a la interpolación. La idea básica se muestra en 6.10. El método interpola la función\(f(t,y)\) en los puntos\(t_0\) (pasado),\(t_1\) (presente) y\(t_2\) (futuro) usando el polinomio Lagrange\[\begin{gathered} f(t) = \frac{(t-t_{n+1})(t-t_{n+2})}{(t_{n}-t_{n+1})(t_{n}-t_{n+2})} f_{n} +\frac{(t-t_{n})(t-t_{n+2})}{(t_{n+1}-t_{n})(t_{n+1}-t_{n+2})} f_{n+1} \\ \nonumber +\frac{(t-t_{n})(t-t_{n+1})}{(t_{n+2}-t_{n})(t_{n+2}-t_{n+1})} f_{n+2}\end{gathered} \tag{eq: 6.10} \] por lo que la iteración es\[\tag{eq:6.11} y_{n+2} = \int_{t_{n+2}}^{t_{n+3}} \frac{(t-t_{n+1})(t-t_{n+2})}{2 h^2} f_{n} +\frac{(t-t_{n})(t-t_{n+2})}{-h^2} f_{n+1} +\frac{(t-t_{n})(t-t_{n+1})}{2 h^2} f_{n+2} dt + y_{n+1}\] Note que\(f_{n+2} = f(t_{n+2}, y_{n+2})\) así \(y_{n+2}\)aparece en ambos lados de [eq:6.11] — el método es implícito. Sin embargo, podemos tratarlo como un factor constante\(f_{n+2}\) y seguir adelante y realizar la integral. Cambiar variables como de costumbre:\(\alpha = (t-t_0)/h\) así\(h d\alpha = dt\) y la integral se vuelve\[\tag{eq:6.12} y_{n+2} = h \int_1^2 \frac{(\alpha-1)(\alpha-2)}{2} f_{n} -\alpha(\alpha-2) f_{n+1} +\frac{\alpha(\alpha-1)}{2} f_{n+2} dt + y_{n+1}\]

Figura 6.10: Método Adams-Moulton de tercer orden.

Evaluar cada término arroja el método Adams-Moulton de tercer orden:\[\tag{eq:6.13} y_{n+2} = h \left( -\frac{1}{12} f_n + \frac{2}{3} f_{n+1} + \frac{5}{12} f_{n+2} \right) + y_{n+1}\] De nuevo\(f_{n+2} = f(t_{n+2}, y_{n+2})\), ya que, la ecuación [eq:6.13] debe resolverse usando un rootfinder para obtener\(y_{n+2}\), pero ya debería estar cómodo con tales métodos implícitos.

Ejemplo: métodos Adams y el oscilador Van der Pol

Aquí hay una demostración rápida que muestra por qué métodos implícitos como Adams-Moulton son útiles, a pesar de requerir un rootfinder.

Figura 6.11: Método Adams-Bashforth de tercer orden resolviendo el sistema Van der Pol. \(0.01\)Se utilizaron estepsices\(h = 0.1\) y. El método es claramente inestable para\(h = 0.1\) — el eje y de la gráfica toca fondo en -1e177, lo que indica que la solución ha explotado! El método es estable\(h = 0.01\) pero no es tan preciso como el método Adams-Moulton mostrado en 6.12.

Figura 6.12: Método Adams-Moulton de tercer orden para resolver el sistema Van der Pol. Los hermanastros fueron\(h = 0.1\) y\(0.01\). En contraste con el resultado de Adams-Bashforth mostrado en 6.11, el método Adam-Moulton se mantiene estable para\(h = 0.1\).

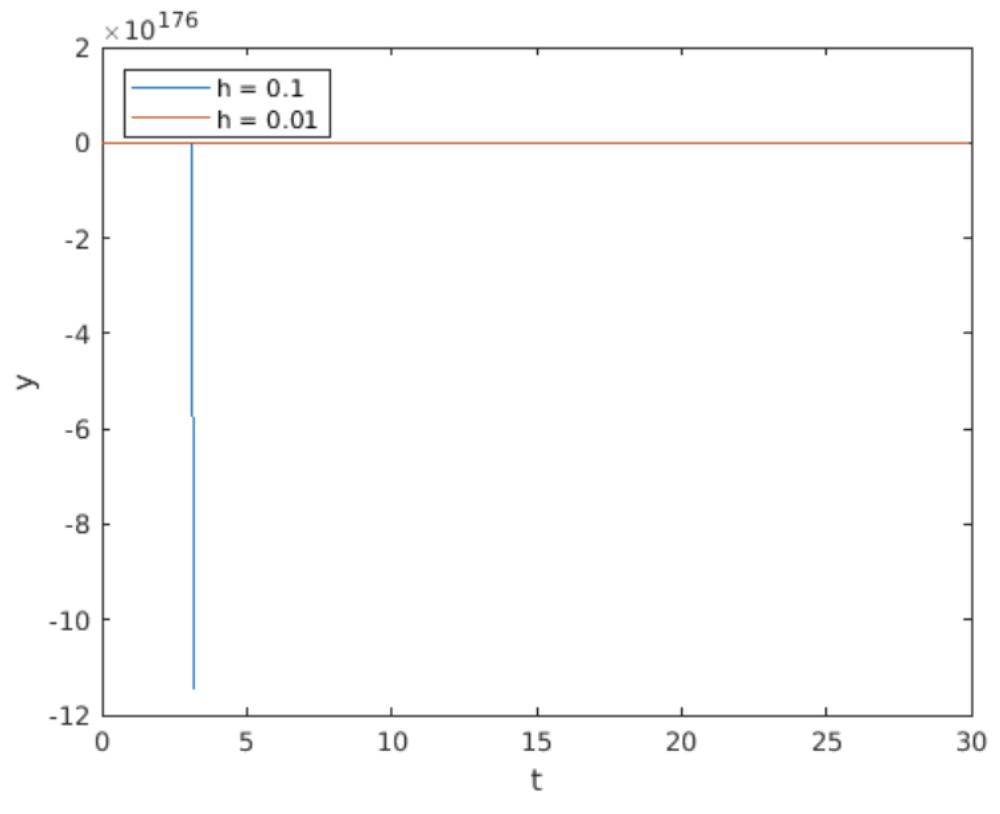
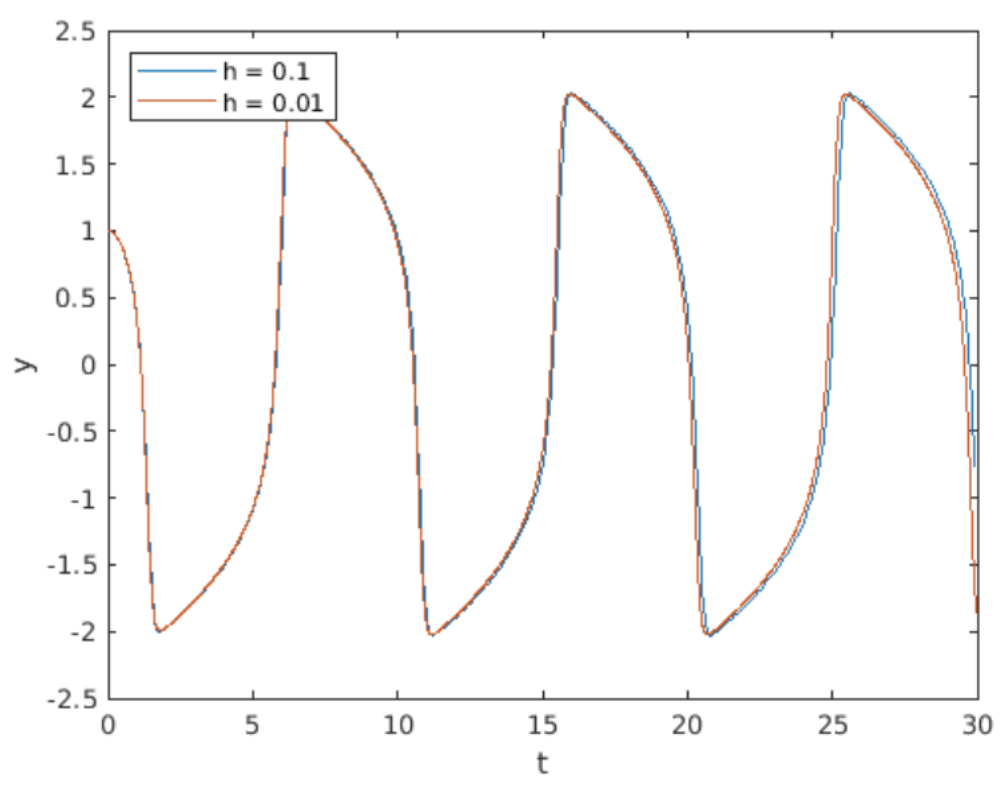
He escrito programas implementando Adams-Bashforth de 3er orden y Adams-Moulton de 3er orden para integrar el oscilador Van der Pol [eq:4.5]. Recordemos que el sistema Van der Pol es rígido, y una buena práctica recomienda utilizar métodos implícitos al integrar ODEs rígidos. La razón es que los sistemas implícitos pueden usar estepsias más grandes sin dificultad, por lo que pueden resolver rápidamente un sistema rígido que obligaría a un método explícito como Adams-Bashforth a usar pequeños pasos.

En 6.11 y 6.12 se muestran gráficas de la solución de Van der Pol calculadas por Adams-Bashforth de 3er orden (explícito) vs Adams-Moulton de 3er orden (implícito). Ambos solucionadores utilizaron tamaño de paso\(h = 0.1\). A primera vista, el resultado del cálculo de Adams-Bashforth parece extraño. La razón es que el método Adams-Bashforth se volvió inestable, por lo que su producción explotó a aproximadamente\(y = -1e177\) — el método es inútil para Van der Pol en este tamaño de paso. (Por supuesto, puede disminuir el tamaño de paso a costa de un tiempo de simulación más largo. Eso no es un problema para este problema de juguete, pero si te enfrentas a un cálculo grande que lleva muchas horas, quieres exprimir el mayor rendimiento posible de tu método). Por otro lado, Adams-Moulton funciona bien en este tamaño de paso.

Debo mencionar que hay una compensación entre estos dos métodos: Adams-Bashforth requiere un tamaño de paso mucho más pequeño para manejar el sistema Van der Pol, pero Adams-Moulton ejecuta un solucionador no lineal (fslove () de Matlab) en cada paso. Los solucionadores suelen ser iterativos, por lo que pueden tomar un tiempo significativo para converger en una solución. Por lo tanto, Adams-Bashforth requiere menos cómputos por paso, pero es inestable a menos que el tamaño del paso sea pequeño. Por otro lado, el método Adams-Moulton toma más tiempo por paso, pero se mantiene estable para las estepsias más grandes. Qué método elegir depende de los detalles particulares de su problema; normalmente necesita experimentar con diferentes métodos y diferentes hermanastros para encontrar la mejor manera de resolver su problema particular.

Generalizaciones

Existe toda una familia de métodos lineales multipaso de órdenes 2, 3, 4, 5, 6, y así sucesivamente. El patrón general empleado por estos métodos se ve así:\[\label{eq:LMMGeneralOrder} \alpha_0 y_i + \alpha_1 y_{i+1} + \alpha_2 y_{i+2} + \cdots + y_{i+k} = h \left(\beta_0 f_i + \beta_1 f_{i+1} + \beta_2 f_{i+2} + \cdots + \beta_{k} f_{i+k} \right)\] Estos se llaman métodos\(k\) -step. Algunas cosas a tener en cuenta:

• El coeficiente frente al término\(y_{i+k}\) en el LHS es uno. Este es el valor futuro que deseamos encontrar.
• Si establecemos todos\(\alpha_j = 0\) excepto\(\alpha_{k-1}\) y además establecemos\(\beta_{k}=0\) entonces recuperamos los métodos explícitos de Adams-Bashforth.
• Si establecemos todos\(\alpha_j = 0\) excepto\(\alpha_{k-1}\) y mantenemos distintos de cero\(\beta_{k}\) entonces obtenemos los métodos Adams-Moulton.
• No lo probaré aquí, pero se puede demostrar que un método\(k\) -step Adams-Bashforth tiene orden\(O(h^k)\) mientras que un método\(k\) -step Adams-Moulton tiene orden\(O(h^{k+1})\). Esa es otra ventaja de lo implícito sobre los métodos explícitos.
• Mantener\(\alpha_j\) términos adicionales da los llamados métodos de diferencia hacia atrás. Esos métodos están fuera del alcance de esta clase.
• En cuanto a la estabilidad de los métodos lineales multietapa, existe un gran cuerpo de teoría bien desarrollada que especifica las condiciones bajo las cuales son estables. Esa teoría también está fuera del alcance de esta clase.

Los métodos lineales multipaso de alto orden como estos se implementan en solucionadores de ODE de alta gama como la suite Sundials de Lawrence Livermore National Laboratories. Lo más probable es que en su trabajo simplemente llame a ese solucionador “enlatado” en lugar de escribir el suyo propio, por lo que se le ahorran las complejidades de implementar dicho solucionador.

Resumen del capítulo

Estos son los puntos importantes que se hacen en este capítulo:

• Los métodos lineales de múltiples pasos se derivan interpolando puntos previamente calculados (y a veces futuros) y usando la interpolación en [eq:6.2] para calcular puntos de solución en el futuro.
• El orden de los métodos lineales multipaso se incrementa incorporando más puntos de interpolación en la aproximación interpolada para\(f(t, y)\). Se examinaron los métodos trapecio (primer orden), Adams-Bashforth (2do y 3er orden) y Adams-Moulton (3er orden).
• Los métodos de Adams-Bashforth son explícitos, Adams-Moulton son implícitos.
• Los métodos implícitos como Adam-Moulton se recomiendan para sistemas rígidos, ya que permanecen estables al tiempo que permiten pasos más grandes que los métodos explícitos. Sin embargo, los métodos implícitos requieren ejecutar un rootfinder en cada paso, por lo que existe una compensación de rendimiento entre métodos explícitos e implícitos.
• Los métodos examinados en este capítulo son miembros de una gran clase de métodos lineales multipaso descritos por [eq:6.14]. Dichos métodos se proporcionan comúnmente en solucionadores de ODE de alta gama.