1.7: Integradores Symplectic

Integradores Symplectic

ODEs de conservación de energía

Los solucionadores de ODE examinados hasta ahora están destinados a aplicaciones de propósito general. Sin embargo, se trata de un conjunto especial de ODE que no son bien servidos por los métodos de propósito general. Se trata de ODE que describen sistemas mecánicos sometidos a movimiento sin pérdidas. “Sin pérdidas” significa que el sistema no disipa energía. Algunos ejemplos son:

• El oscilador armónico simple sin fricción, que ya hemos visto muchas veces.
• El péndulo colgante sin fricción.
• Movimiento de planetas o satélites en el espacio.

Podrías considerar los dos primeros ejemplos como modelos sobredimensionados. Sin embargo, un péndulo que se balancea al vacío está muy cerca de no tener pérdidas. El aparato LIGO que detectó ondas gravitacionales utilizó péndulos colgados en el vacío como parte de su funcionamiento, por lo que el péndulo (casi) sin fricción es una realidad física. Además, el movimiento de los objetos en el espacio ocurre casi sin disipación — no hay atmósfera que proporcione resistencia al movimiento. Simular con precisión su movimiento requiere solucionadores de ODE que respeten el hecho de que no experimentan fricción cuando se mueven, no disipan ninguna energía. Desafortunadamente, el problema con los solucionadores de ODE estudiados hasta el momento es que ninguno de ellos conserva energía. Si quieres calcular la trayectoria que debe recorrer un cohete para atracar con la estación espacial en órbita, es crucial que tu solucionador de ODE calcule la trayectoria perfectamente, y eso significa que necesita trayectorias de cómputos que son conservadoras de energía.

¿Qué es la energía? En una clase de física probablemente aprendiste que la energía es algo que se conserva. Pero, ¿qué significa eso? ¿Y por qué es la energía cinética\((1/2) m v^2\)? ¿Qué está pasando, matemáticamente?

Para algunas percepciones volvemos una vez más al simple oscilador armónico,\[\tag{eq:7.1} m \frac{d^2 y}{d t^2} = -k y\] Asociado a esta ecuación se encuentra una llamada energía,\[\tag{eq:7.2} E = \frac{1}{2} m \left( \frac{d y}{d t} \right)^2 + \frac{1}{2} k y^2\] que es una función de las variables posición\(y\) y velocidad\(dy/dt\). Desde tu clase de física puedes reconocer el término de la izquierda como la “energía cinética” y el término de la derecha como la “energía potencial” del SHO. La propiedad importante de esta definición energética es que cualquier solución\(y(t)\) de la ODE [eq:7.1] conservará automáticamente la función energética [eq:7.2]. “Conservar” significa que la energía\(E\) se mantendrá constante para todo momento. Esto se puede demostrar considerando la derivada de tiempo de\(E\). \[\frac{d E}{d t} = m \left( \frac{d y}{d t} \right)\left( \frac{d^2 y}{d t^2} \right) + k y \left( \frac{d y}{d t} \right) \tag{eq:7.3}\]luego sustituya el valor de\(m (d^2 y/d t^2)\) from [eq:7.1] en esta ecuación para obtener

\[\frac{d E}{d t} = -k y \left( \frac{d y}{d t} \right) + k y \left( \frac{d y}{d t} \right) \tag{eq:7.4}\]

\[ = 0 \tag{7.5}\]

Esto dice que\(E\) nunca cambia — se conserva por cualquier solución a [eq:7.1]. En general, algunas —pero no todas— las ODE admiten una energía que se conserva. La forma exacta de la energía depende de la ODE que se esté considerando. Pero si existe una energía conservada para una ODE en particular, entonces un buen solucionador debería producir soluciones que conserven energía. Desafortunadamente, la mayoría de los solucionadores no lo hace.Esto lo hemos visto varias veces a lo largo de este folleto —ver 2.9, 3.5, 4.5 y 4.13. Todas esas cifras muestran la amplitud de la oscilación creciendo o disminuyendo con el aumento del tiempo, comportamiento que evidencia que la energía está cambiando con el tiempo.

Hay una clase de solucionadores que sí conservan energía. Caen bajo la rúbrica “integradores simplécticos”. El motivo por el que tienen este nombre tiene que ver con la mecánica hamiltoniana, una generalización de la mecánica newtoniana que tocaremos en 7.4. Los integradores simplécticos se utilizan únicamente para las ODE de segundo grado como las que se encuentran en la segunda ley de Newton. En consecuencia, son muy importantes para calcular el movimiento de los objetos en el espacio, incluyendo planetas, naves espaciales, cometas, etc. Vienen en muchos órdenes de precisión, similares a los otros solucionadores discutidos en este folleto. Solo voy a discutir aquí el método más simple —el simpléctico Euler— ya que estos integradores simplécticos son un tema especializado y basta con ver simplemente los conceptos en lugar de revisar todo el campo.

Simplectic Euler

Como se mencionó anteriormente, los integradores simplécticos se utilizan para resolver ODEs de segundo grado.L Eso significa que los integradores se aplican a un sistema de dos ODEs de primer grado. Es decir, comenzamos con el sistema para resolver\[\begin{aligned} \frac{d u}{d t} =& f(t, v) \\ \frac{d v}{d t} =& g(t, u) \end{aligned} \tag{eq:7.6}\] Con esta definición, aquí está simplectic Euler:\[\begin{aligned} v_{n+1} =& v_n + h g(t_n, u_n) \\ u_{n+1} =& u_n + h f(t_n, v_{n+1}) \end{aligned} \tag{eq:7.7}\] Tenga en cuenta que primero\(v\) se actualiza, luego\(u\) nos actualiza utilizando el ya actualizado\(v\). El método es simétrico con respecto al cual se actualiza primero,, así que también puedes usar\[\begin{aligned} u_{n+1} =& u_n + h f(t_n, v_{n}) v_{n+1} =& v_n + h g(t_n, u_n+1) \\ \end{aligned} \tag{eq:7.8}\] Esto a veces se denomina método semiimplícito (o esquema Euler semi-implícito) ya que el valor actualizado\(v_{n+1}\) (o\(u_{n+1}\)) se usa en medio del cálculo completo de dos pasos.

Ejemplo: el oscilador armónico simple

Conocemos las soluciones analíticas de la ecuación del oscilador armónico simple [eq:7.1] para conservar energía. Ahora veremos si la solución producida por el simpléctico Euler también conserva energía. Para el RHS de [eq:7.6] tenemos\[\begin{aligned} \nonumber f(t, v) =& -\omega^2 v \\ \nonumber g(t, u) =& u\end{aligned}\] usando la definición habitual\(\omega^2 = k/m\). Insertando estos en [eq:7.8] rendimientos\[\begin{aligned} v_{n+1} =& v_n + h u_n \\ u_{n+1} =& u_n - h \omega^2 v_{n+1} \end{aligned} \tag{eq:7.9}\] Podríamos implementar este sistema en la computadora tal como está, pero para fines de análisis de estabilidad lo convertiremos en una forma de propagador matricial. Para ello trasladar el futuro al LHS y el presente al RHS. Obtenemos\[\nonumber \begin{aligned} u_{n+1} + h \omega^2 v_{n+1} =& u_n \\ v_{n+1} =& v_n + h u_n \end{aligned}\]

Ahora escribe ambos lados como productos matriz-vector. Obtenemos\[\nonumber \begin{pmatrix} 1 & h \omega^2 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} u_{n+1} \\ v_{n+1} \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ h & 1 \end{pmatrix} \begin{pmatrix} u_{n} \\ v_{n} \end{pmatrix}\] Ahora mueve la matriz LHS a la RHS\[\nonumber \begin{pmatrix} u_{n+1} \\ v_{n+1} \end{pmatrix} = \begin{pmatrix} 1 & h \omega^2 \\ 0 & 1 \end{pmatrix}^{-1} \begin{pmatrix} 1 & 0 \\ h & 1 \end{pmatrix} \begin{pmatrix} u_{n} \\ v_{n} \end{pmatrix}\] Simplifying, esto se convierte en\[\begin{pmatrix} u_{n+1} \\ v_{n+1} \end{pmatrix} = \begin{pmatrix} 1 - h^2 \omega^2& -h \omega^2 \\ h & 1 \end{pmatrix} \begin{pmatrix} u_{n} \\ v_{n} \end{pmatrix} \tag{eq:7.10}\]

Esto define un método de iteración usando la matriz como propagador. Observe la similitud con la matriz de propagación de Euler hacia adelante [eq:2.19]: solo el elemento (1,1) es diferente. Los resultados de la implementación de esta iteración se muestran en 7.1. A diferencia de los casos de Euler hacia adelante y hacia atrás, este método no evidencia crecimiento ni decaimiento de la amplitud de oscilación con el tiempo.

Figura 7.1: El oscilador armónico simple integrado utilizando Euler simpléctico. Tenga en cuenta el lapso de tiempo más largo que el trazado para las soluciones anteriores del SHO. Ningún crecimiento ni decaimiento de la oscilación es evidente en esta gráfica — la energía de la solución es conservada por el método, al menos en esta escala.

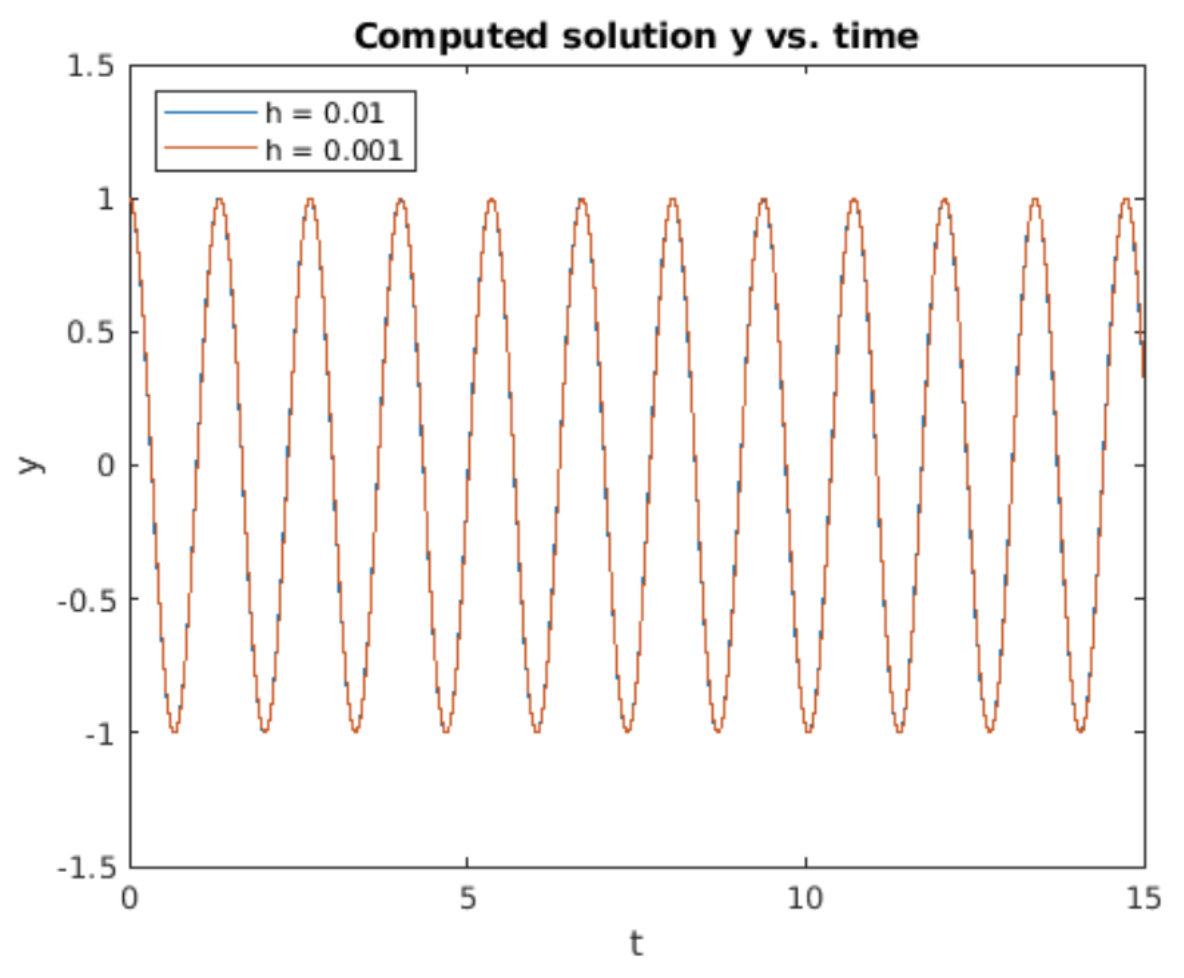
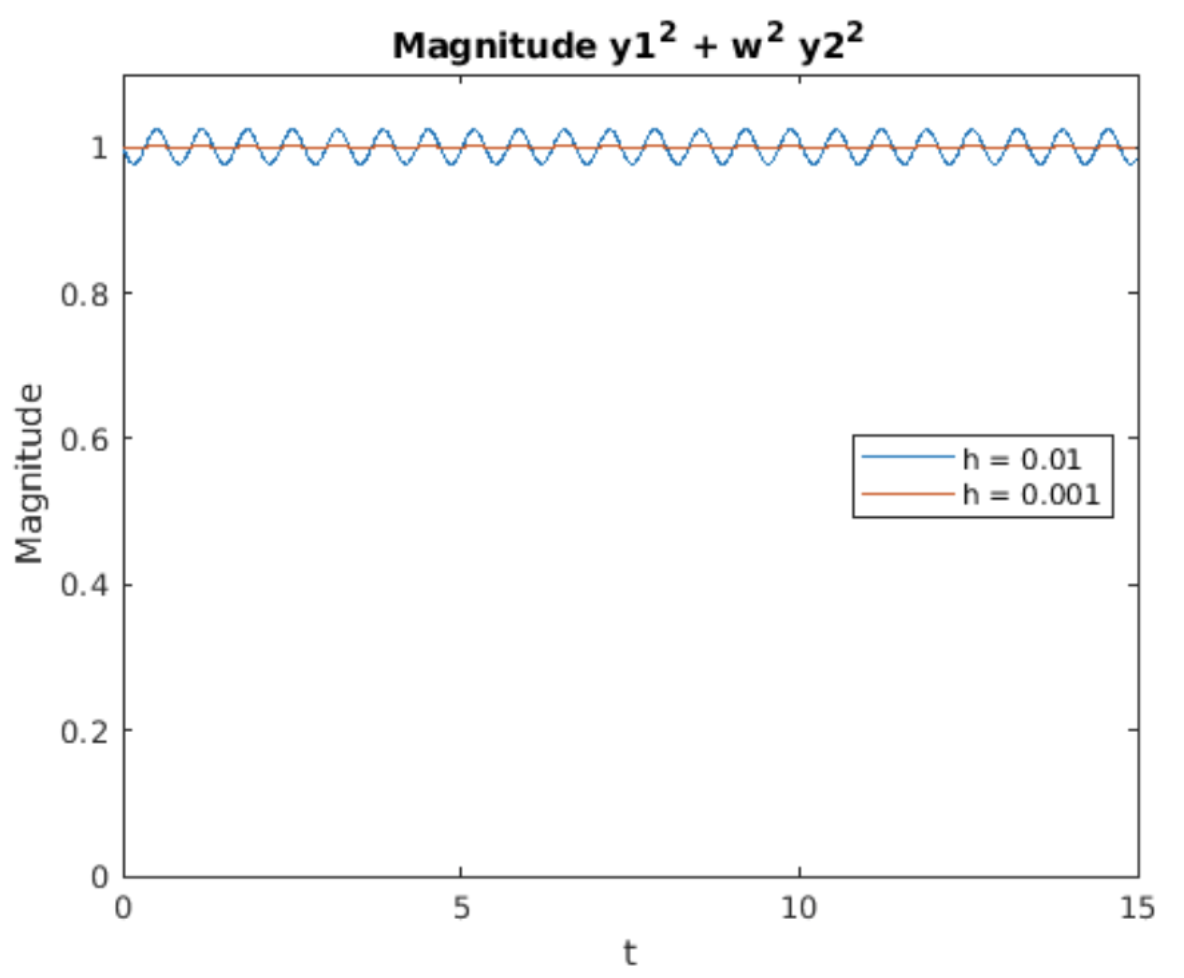
La conservación de energía también se muestra en 7.2 que parcelas\(u(t)^2 + \omega^2 v(t)^2\). En analogía a\(\sin^2(t) + cos^2(t) = 1\), la energía\(u(t)^2 + \omega^2 v(t)^2\) debe permanecer constante. Lo hace, salvo que pone de manifiesto pequeños meneos que dependen del tiempo. Tenga en cuenta que el valor promedio sigue siendo igual a uno.

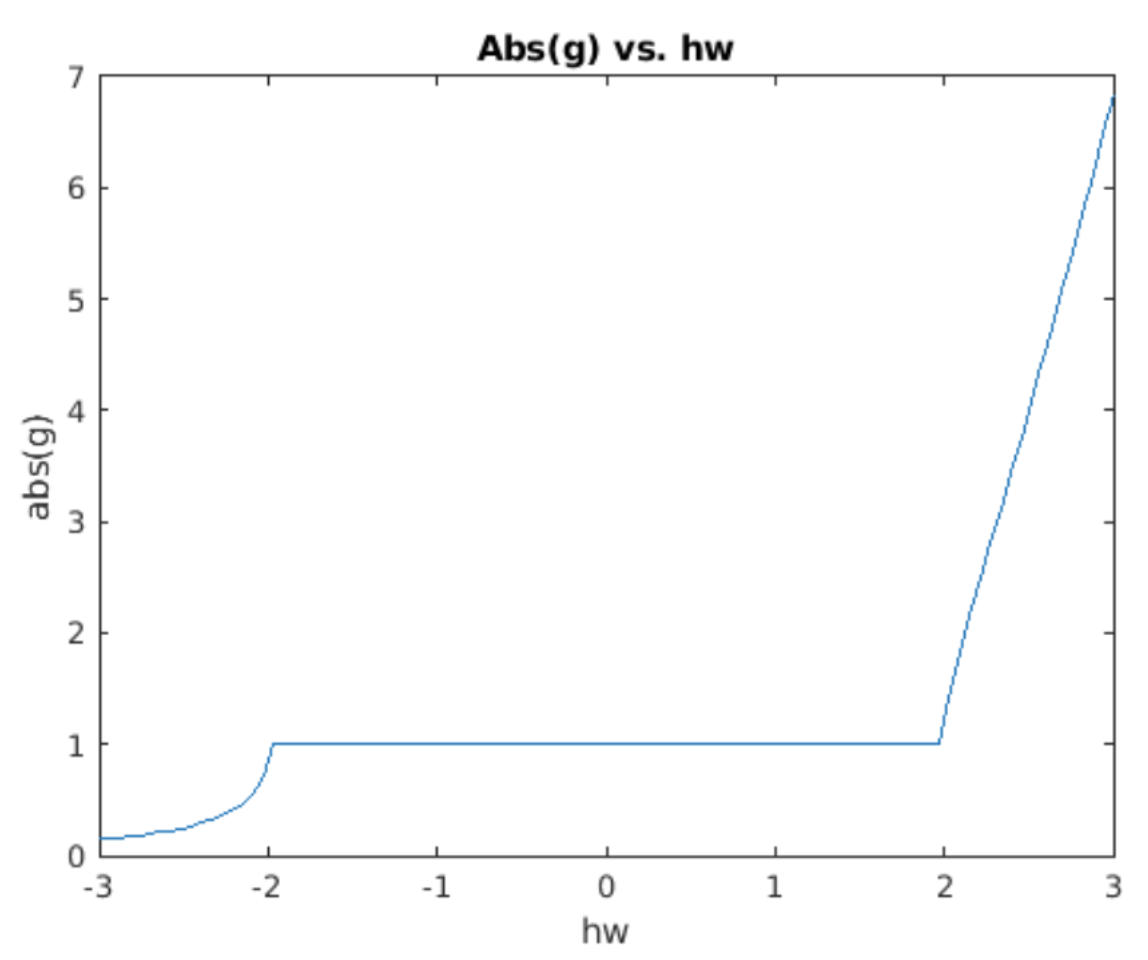
Por supuesto, ahora la pregunta es ¿por qué el simpléctico Euler conserva energía? Como es habitual, la respuesta radica en computar los valores propios de la matriz propagadora. Llamar\(g\) al valor propio (de nuevo, para “factor de crecimiento”). La ecuación del valor propio es entonces\[\nonumber det \begin{pmatrix} 1 - h^2 \omega^2 - g & -h \omega^2 \\ h & 1 - g \end{pmatrix} = 0\] Resolver para\(g\) da\[\tag{eq:7.11} g = 1 - \frac{h^2 \omega^2}{2} \pm \frac{h \omega \sqrt{h^2 \omega^2 - 4}}{2}\] Esta es una expresión desagradable a primera vista. No obstante, nuestro objetivo es ver si\(|g| = 1\) por algún valor de\(h \omega\). Si\(|g| = 1\) entonces tenemos un método que no hace que la amplitud de la solución crezca o decaiga. Por lo tanto, una manera fácil de entender [eq:7.11] es simplemente usar Matlab para trazar\(|g|\) vs\(h \omega\). Esto se muestra en 7.3. Eso lo vemos\(|g| = 1\) cuando\(|h \omega| < 2\). Por lo tanto, el método simpléctico de Euler mantiene la amplitud del oscilador armónico simple, es decir, conserva energía.

Figura 7.2: Una gráfica de la\(u(t)^2 + \omega^2 v(t)^2\) cual muestra que Euler simpléctico conserva energía en promedio. Tenga en cuenta que la amplitud permanece cerca de uno durante todo el tiempo de simulación. Se mueve hacia arriba y hacia abajo pero no crece ni se encoge en una escala de tiempo más larga.

Saber que\(|g| = 1\) cuando nos\(|h \omega| < 2\) permite dar algunos pasos analíticos fáciles adicionales. Cuando\(|h \omega| < 2\) el término más a la derecha en [eq:7.11] es puro imaginario mientras que los otros dos términos son reales. Eso significa que podemos calcular\(|g|^2 = \Re(g)^2 + \Im(g)^2\),\[\nonumber |g|^2 = \left(1 - \frac{h^2 \omega^2}{2}\right)^2 + \left( \frac{h \omega \sqrt{4 - h^2 \omega^2}}{2} \right)^2\]\[\nonumber = \left(1 - h^2 \omega^2 + \left( \frac{h^2 \omega^2}{2} \right)^2 \right) + \left( \frac{h^2 \omega^2 (4 - h^2 \omega^2)}{4} \right)\]\[\nonumber = 1\] como se encontró en la parcela 7.3. Esto confirma nuestra observación numérica en 7.3 que\(|g| = 1\). Fuera de este rango, el factor de crecimiento no es uno, lo que significa que el simpléctico Euler no conserva energía fuera del rango\(|h \omega| < 2\). Sin embargo, esto no es una gran limitación ya que generalmente se\(h \ll 1/\omega\) necesita calcular oscilaciones suaves. Es decir, es necesario muestrear al menos un par de puntos dentro de cada oscilación para simularla con precisión, por lo que lograr\(|h \omega| < 2\) es compatible con elegir un buen tamaño de paso.

Figura 7.3: El factor de crecimiento\(|g|\) graficado vs\(h \omega\). El factor de crecimiento es exactamente uno cuando\(|h \omega| < 2\). Por lo tanto, en este rango el método simpléctico de Euler mantiene la amplitud del oscilador armónico simple, es decir, conserva energía. Sin embargo, las parcelas se alejan entre sí en el tiempo dependiendo del valor de\(h\).

Sistemas conservadores, espacio de fase y teorema de Liouville

Esta sección es un breve desvío hacia la física de la conservación de energía en la mecánica clásica. Al inicio del 7 anterior mencioné que algunas, pero no todas las ODE tienen una energía acompañante. En la mecánica avanzada, las ecuaciones de movimiento de un sistema que conserva energía se encuentran escribiendo primero un llamado “hamiltoniano”, y luego derivando la posición y el impulso de todas las partículas en el sistema del hamiltoniano. El hamiltoniano es una función escalar que desempeña el papel de la energía del sistema, pero se escribe en términos de variables de posición e impulso. Para el SHO, el hamiltoniano es\[\tag{eq:7.12} H(p,x) = \frac{p^2}{2 m} + \frac{1}{2} k x^2\] donde\(p\) está el impulso del oscilador y\(x\) es su posición. Tenga en cuenta que esto es lo mismo que la energía total [eq:7.2] donde hemos reemplazado la energía cinética escrita en términos de la velocidad\(m v^2 / 2\) con la expresión equivalente escrita en términos de impulso,\(p^2/2 m\). Entonces, para obtener las ecuaciones de movimiento del sistema, el formalismo hamiltoniano dice que se encuentran a partir de las ecuaciones de Hamilton,\[\tag{eq:7.13} \frac{d x}{d t} = \frac{\partial H}{ \partial p}\]\[\tag{eq:7.14} \frac{d p}{d t} = -\frac{\partial H}{ \partial x}\] En el caso del SHO utilizamos el hamiltoniano [eq:7.12] y estas ecuaciones para obtener las ecuaciones de movimiento del oscilador,\[\nonumber \frac{d x}{d t} = \frac{p}{m}\] \[\nonumber \frac{d p}{d t} = -k x\]Este par de ecuaciones debería recordarte fuertemente a las introducidas en [eq:2.17] — son las mismas ecuaciones pero escritas en términos de posición e impulso en lugar de posición y velocidad. En la mecánica hamiltoniana, primero usas el razonamiento físico para construir y escribir a un hamiltoniano. Entonces se derivan las ecuaciones de movimiento del hamiltoniano usando estas ecuaciones. El punto es que la mecánica hamiltoniana te da un procedimiento general, paso a paso para derivar las ecuaciones de movimiento de cualquier sistema. Por el contrario, la mecánica newtoniana se basa en argumentos ad-hoc sobre fuerzas y aceleraciones para derivar las ecuaciones de movimiento, y cada sistema se maneja de manera diferente dependiendo de su configuración física.

Dado que el hamiltoniano es la función energética del sistema, se conserva siempre y cuando el tiempo no aparezca explícitamente en su fórmula. Este es claramente el caso del SHO hamiltoniano, [eq:7.12]. A nivel profundo, la conservación de energía es consecuencia del teorema de Noether, que dice que toda simetría del hamiltoniano implica una cantidad conservada correspondiente. Para el hamiltoniano SHO, podemos reemplazar el tiempo\(t\) con\(t + \tau\), donde\(\tau\) representa un desplazamiento constante del eje del tiempo. Al realizar este reemplazo\(t \rightarrow t + \tau\), la forma del hamiltoniano sigue siendo la misma. Es decir, este hamiltoniano es invariante con respecto a la transformación\(t \rightarrow t + \tau\). Otra forma de decirlo es que el hamiltoniano es simétrico con respecto a los turnos de tiempo. Como consecuencia del teorema de Noether, esta simetría implica que se conserva una cantidad asociada, y en este caso la cantidad conservada es la energía. Esto debería responder a la pregunta planteada en 7.1, ¿por qué se conserva la energía para el SHO? ¡La energía es conservada por el SHO porque su hamiltoniano tiene simetría de cambio de tiempo! El teorema de Noether es muy profundo y es utilizado por los físicos para razonar sobre muchas cantidades conservadas diferentes como carga eléctrica, masa, paridad y otras cantidades. Desafortunadamente, si bien es muy interesante, una mayor discusión del teorema de Noether está muy fuera del alcance de este folleto.

Otro resultado importante de la mecánica clásica es que cualquier sistema derivado de un hamiltoniano invariante en el tiempo conservará volúmenes en el espacio de fase. ¿Qué significa esto?

• Primero, el espacio de fase se define como el espacio de todos los estados posibles del sistema. Por ejemplo, un cuerpo sometido a movimiento unidimensional tiene un espacio de fase bidimensional: el conjunto de todas las posiciones y momentos posibles,\([x, p]\) sin tener en cuenta ninguna ecuación de movimiento. (Las ecuaciones de movimiento se impondrán más adelante y naturalmente restringirán el conjunto de posibles\([x, p]\) órbitas dentro del espacio de fase completo).
• Una vez definido el espacio de fase, cualquier sistema mecánico particular puede describirse a través de un hamiltoniano definido en el espacio de fase. Diferentes sistemas mecánicos serán descritos por diferentes hamiltonianos. Por ejemplo, el SHO tiene hamiltoniano\(H = p^2/2m + k x^2/2\) mientras que el péndulo colgante tiene hamiltoniano\(H = p^2/2m + m g \cos(\theta)/2\).
• Un hamiltoniano invariante en el tiempo es aquel que no tiene una dependencia explícita del tiempo; la variable\(t\) no aparece en su fórmula. Este es obviamente el caso del SHO hamiltoniano [eq:7.12].
• Las ecuaciones de movimiento derivadas del hamiltoniano definirán cómo\([x(t),p(t)]\) evolucionará en el tiempo cualquier punto en particular. Se puede visualizar la evolución de un solo punto como una trayectoria que se mueve a través del espacio de fase.
• A continuación, considere una pequeña región del espacio de fase que rodea el punto inicial del espacio de fase\([x(0),p(0)]\). Ver 7.4. Ahora pregunta, qué pasa con el volumen de la región a medida que avanza el tiempo. El teorema de Louiville dice que el volumen se\(V\) mantiene constante a medida que el sistema evoluciona. Es decir, la región azul que se muestra en la figura puede torcerse y deformarse, pero su volumen seguirá siendo el mismo para siempre.

Figura 7.4: El teorema de Liouville dice que los volúmenes de espacio de fase siguen siendo del mismo tamaño cuando el sistema evoluciona bajo la acción de un hamiltoniano (invariable en el tiempo).

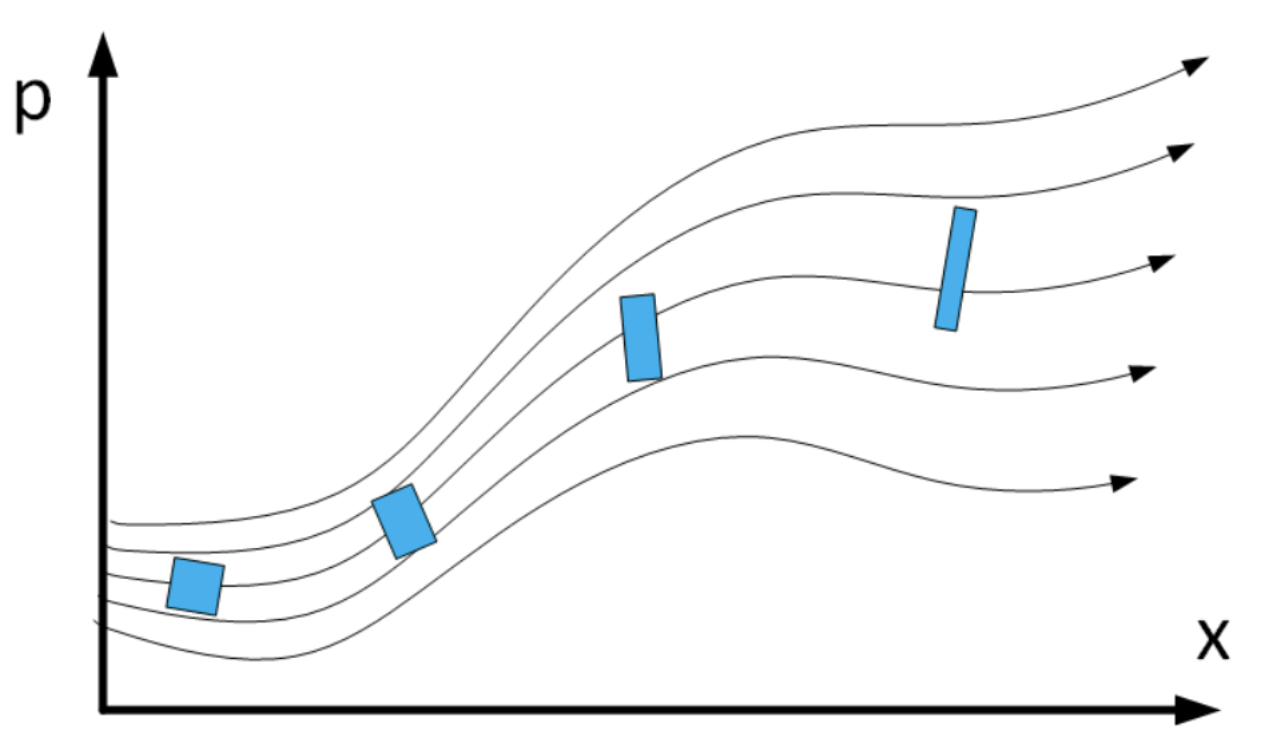
Una prueba general del teorema de Liouville es más difícil de lo que puedo explicar en este folleto. Pero voy a demostrar que\([p(t), x(t)]^T\) las trayectorias generadas por la SHO hamiltoniana conservan volúmenes de espacio de fase, y puedes usar mi demostración como motivación para aceptar el teorema general.

Antes de examinar el SHO, quiero comenzar por considerar lo que significa medir volúmenes en el espacio de fase. También doy un criterio para reconocer cuándo se conserva el volumen bajo una transformación. Utilizaré una imagen muy sencilla para transmitir estas ideas. Consideremos el caso de un pequeño cuadrado en un espacio de fase bidimensional. Tomar los lados del cuadrado para ser definidos por dos vectores,\(u\) y\(v\). Ahora considere lo que sucede a\(u\) y\(v\) bajo una transformación lineal. “Transformación lineal” significa multiplicación matriz-vector. Bajo acción de una\(2 \times 2\) matriz\(T\), tenemos\[\begin{pmatrix} u' \\ v' \end{pmatrix} = T \begin{pmatrix} u \\ v \end{pmatrix} \tag{eq:7.15}\] Pensamos en\([u', v']^T\) como la salida de la transformación, y\(T\) es la cosa que hace la transformación.

En su clase anterior de álgebra lineal probablemente aprendió que aplicar una transformación lineal a un vector produjo una copia estirada y girada del vector de entrada. Si tienes suerte, es posible que hayas visto que aplicar una transformación lineal a un cuadrado (cuyos lados están definidos por dos vectores) produjo una salida paralelepípeda. Esto se muestra en 7.5.

Figura 7.5: La acción de la transformada lineal (matriz)\(T\) sobre vectores\(u\) y\(v\). En cada caso, el resultado transformado\(T u\) y\(T v\) es una copia estirada y rotada del vector original. El cuadrado inicial formado por\(u\) y con ello\(v\) se transforma en un paralelepípedo.

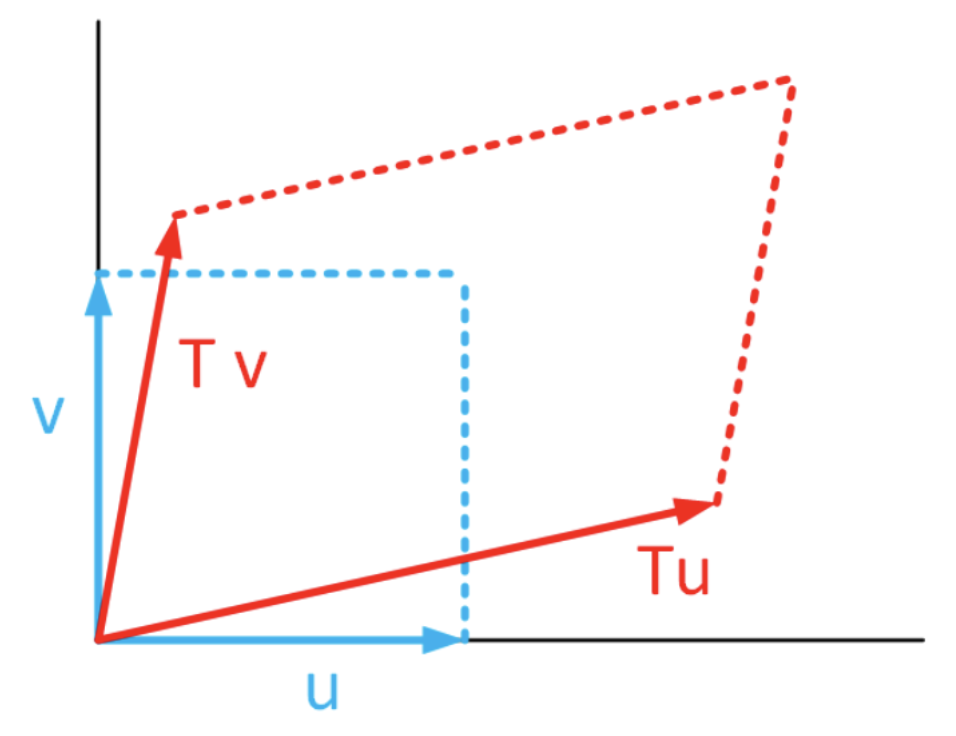
Ahora, ¿cómo calcular el volumen (o área cuando se trabaja en 2D) de estas formas? Recordemos que el área subtendida por los dos vectores se puede encontrar usando la fórmula determinante,\[\begin{aligned} A &= \begin{vmatrix} u_1 & u_2 \\ v_1 & v_2 \end{vmatrix} \\ &= u_1 v_2 - u_2 v_1 \end{aligned} \tag{eq:7.16}\] donde usamos los componentes de los vectores,\(u = [u_1, u_2]^T\) y\(v = [v_1, v_2]^T\). Otra forma de escribir esto es usando una forma cuadrática Se\[\tag{eq:7.17} A = \begin{pmatrix} u_1 & u_2 \\ \end{pmatrix} \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \end{pmatrix} = u_1 v_2 - u_2 v_1\] puede ver fácilmente [eq:7.16] y [eq:7.17] dar el mismo resultado por inspección. Debido a su importancia, le daremos el nombre a la matriz\(J\), así que\ [\ nonumber J =\ begin {pmatrix} 0 & 1\\ -1 & 0\ end {pmatrix}\\\]

Ahora considere lo que significa para una transformación\(T\) conservar el volumen. Para preservar el área requerimos que el área de entrada sea igual al área de salida,\[\begin{aligned} \nonumber u^T J v &= u'^T J v' \\ \nonumber &= u^T T^T J T v\end{aligned}\] o podemos dejar caer el\(u\) y\(v\) y enfocarnos en la transformación misma. Esta ecuación requiere la transformación obedecer\[\tag{eq:7.18} J = T^T J T\] Una transformada lineal (matriz) que obedece [eq:7.18] se llama “simpléctica”. Si una transformación\(T\) es simpléctica, eso significa que conserva volúmenes.

Solo miramos una transformación lineal simpléctica. Pero, ¿qué pasa con el caso de una transformación general? Y ¿qué tiene esto que ver con los hamiltonianos, la conservación de energía y las ODE? Volvamos a anotar el SHO hamiltoniano, esta vez en forma no dimensional. (No quiero tratar de explicar las constantes de masa y rigidez en la siguiente discusión — sólo harían las cosas complicadas). El hamiltoniano es\[\tag{eq:7.19} H = \dfrac{1}{2}p^2 + \dfrac{1}{2} x^2\] Porque el tiempo no aparece explícitamente en este hamiltoniano, el sistema que describe conservará energía. Consideremos ahora el movimiento de un punto\([p, x]^T\) en el espacio de fases gobernado por este hamiltoniano. Las ecuaciones de movimiento obedecidas por el punto son\[\tag{eq:7.20} \dfrac{d}{dt} \begin{pmatrix} p \\ x \end{pmatrix} = \begin{pmatrix} -\partial H / \partial x \\ \partial H / \partial p \end{pmatrix}\] Siguiente considerar la trayectoria de un punto desplazado de\([p, x]^T\) por\([\Delta p, \Delta x]^T\). Imaginamos que estos son los lados del pequeño volumen que queremos rastrear. El movimiento del punto desplazado viene dado por\[\nonumber \frac{d}{dt} \begin{pmatrix} p + \Delta p \\ x + \Delta x \end{pmatrix} = \begin{pmatrix} -\partial H / \partial x \\ \partial H / \partial p \end{pmatrix}\] Suponiendo que ambos\([\Delta p, \Delta x]^T\) son pequeños, podemos aproximar el movimiento usando una expansión de la serie Taylor,\[\tag{eq:7.21} \dfrac{d}{dt} \begin{pmatrix} p + \Delta p \\ x + \Delta x \end{pmatrix} \approx \left. \begin{pmatrix} -\partial H / \partial x \\ \partial H / \partial p \end{pmatrix} \right|_{p,x} + \left. \begin{pmatrix} -\partial^2 H / \partial x \partial p \\ \partial^2 H / \partial p^2 \end{pmatrix} \right|_{p,x} \Delta p + \left. \begin{pmatrix} -\partial^2 H / \partial x^2 \\ \partial^2 H / \partial p \partial x \end{pmatrix} \right|_{p,x} \Delta x\] Ahora resta [eq:7.20] de [eq:7.21], y usar la notación común para derivados parciales para obtener una expresión para la evolución de los lados del pequeño volumen,\[\nonumber \frac{d}{dt} \begin{pmatrix} \Delta p \\ \Delta x \end{pmatrix} \approx \left. \begin{pmatrix} -H_{xp} & -H_{xx} \\ H_{pp} & H_{px} \end{pmatrix} \right|_{p,x} \begin{pmatrix} \Delta p \\ \Delta x \end{pmatrix}\] Esta ecuación dice que el cambio en los lados del cuadrado inicial es impulsado por la matriz de derivadas parciales. Es decir, la matriz derivada parcial juega el papel de la matriz de transformación\(A\) en [eq:7.17]. Por lo tanto, podemos decir que el volumen del cuadrado permanece constante bajo evolución si se mantiene la condición de simplicidad [eq:7.18]. Es decir, para conservar volúmenes de espacio de fase, queremos que se mantenga la siguiente condición para el SHO hamiltoniano:\[\begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} = \begin{pmatrix} -H_{xp} & H_{pp} \\ -H_{xx} & H_{px} \end{pmatrix} \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \begin{pmatrix} -H_{xp} & -H_{xx} \\ H_{pp} & H_{px} \end{pmatrix} \tag{eq:7.22}\] Para el SHO hamiltoniano tenemos\[\begin{aligned} \nonumber H_{xx} &= \frac{\partial^2 H}{\partial x^2} = 1 \\ \nonumber H_{pp} &= \frac{\partial^2 H}{\partial p^2} = 1 \\ \nonumber H_{xp} &= H_{px} = 0\end{aligned}\] Al insertar estos valores en [eq:7.22] y evaluar, obtenemos\[\begin{aligned} \nonumber &\phantom{=i} \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \\ \nonumber &= \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \\ \nonumber &= \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \\ \nonumber &= J\end{aligned}\] Por lo tanto, la matriz de transformación inducida por el SHO Hamiltoniano es simpléctico. Y como es simpléctica, la transformación [eq:7.21] preservará los volúmenes de espacio de fase como se prometió.

Métodos de Euler y conservación de volúmenes espaciales de fase

Terminamos este folleto mirando hacia adelante a Euler y al simpléctico Euler y preguntándonos si uno o ambos conservan volúmenes de espacio de fase. Escribí programas de Matlab que dibujan un rectángulo en el espacio de fases, luego evolucionan los puntos en el rectángulo usando Euler hacia adelante y Euler simpléctico durante cuatro períodos de oscilación.

a) Adelante Euler — alejada. El área bajo estudio comienza como el rectángulo a las 12 horas (arriba) del círculo. Cuatro períodos de oscilación después, el rectángulo obviamente ha crecido de tamaño: el área del espacio de fase no se conserva.

b) Adelante Euler — se amplió.

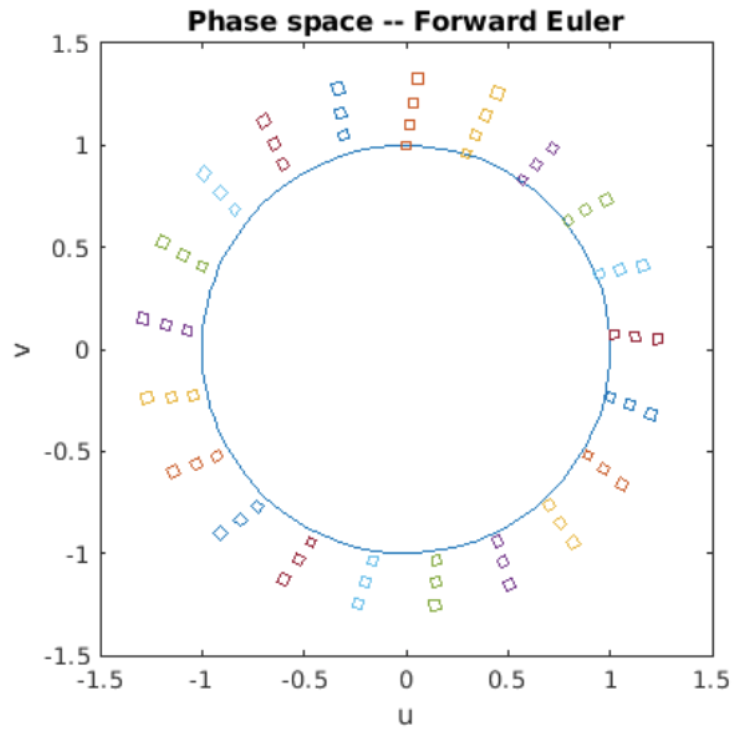
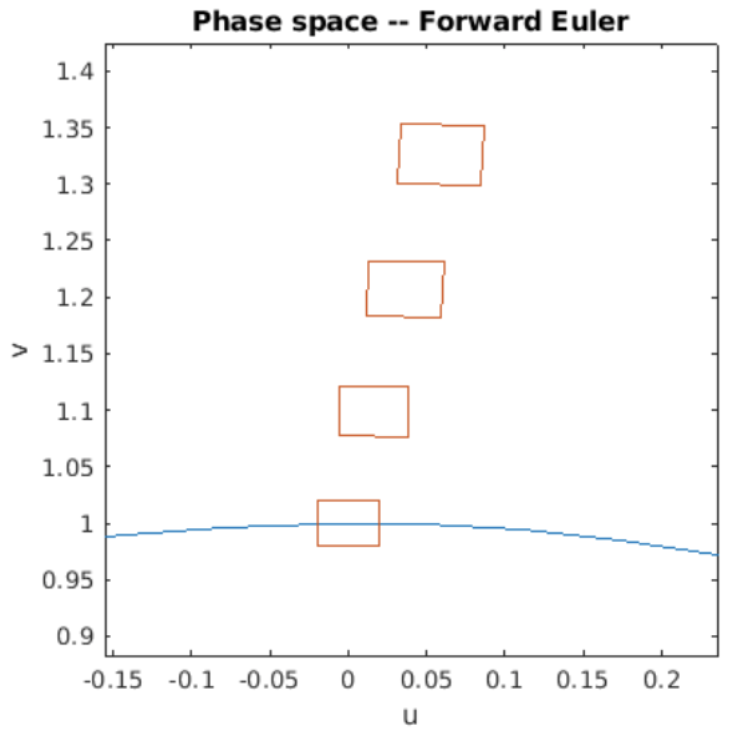
Figura 7.6: Volúmenes de espacio de fase evolucionados por Euler hacia adelante.

a) Euler simplectic — alejada. El área bajo estudio comienza como el rectángulo a las 12 horas (arriba) del círculo. Cuatro periodos de oscilación después el rectángulo no ha crecido de tamaño, ni ha salido del círculo. El método es estable y conservador de energía.

b) Euler simpléctico — con zoom.

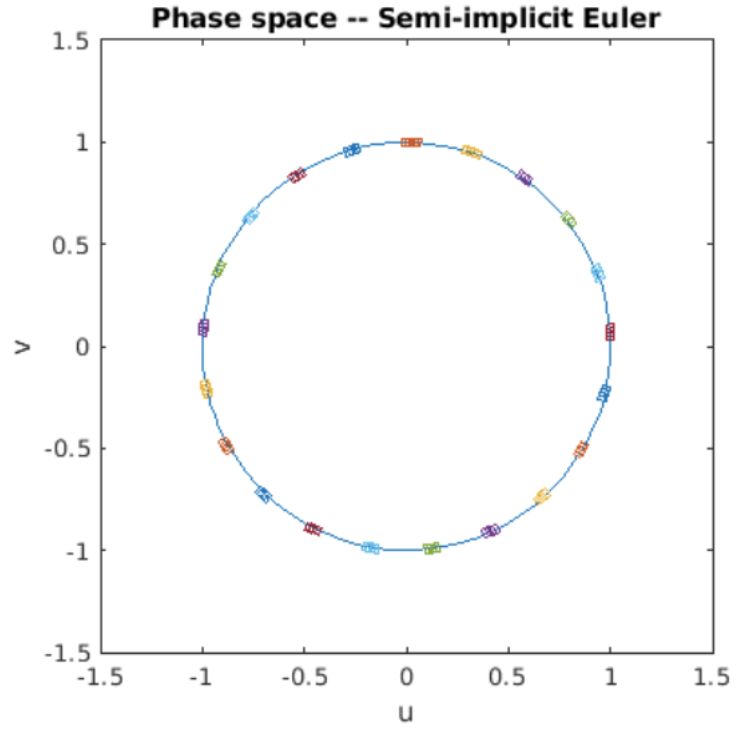
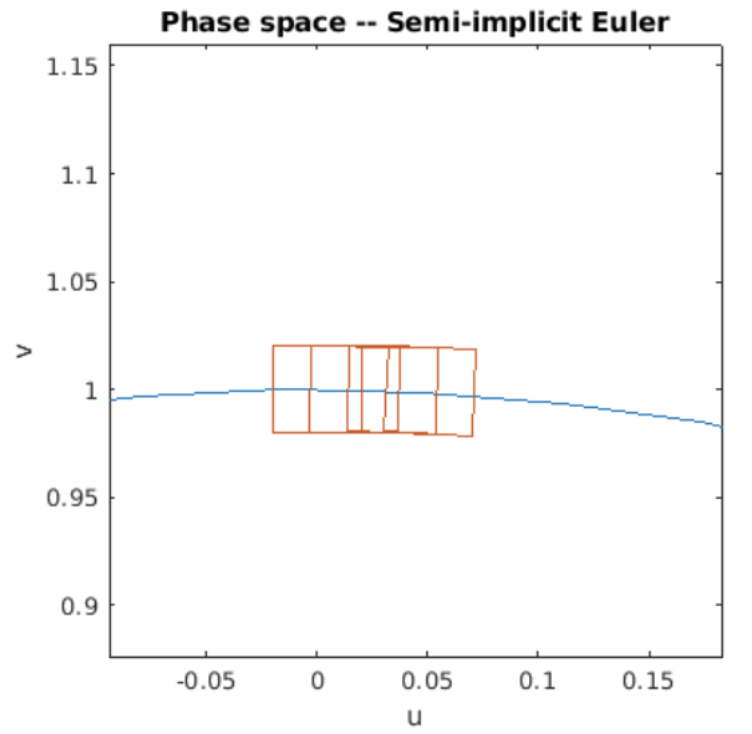
Figura 7.7: Volúmenes espaciales de fase evolucionados por Euler simpléctico.

El programa toma una instantánea del rectángulo varias veces durante su evolución, y traza los rectángulos en el círculo de energía constante. Los resultados de la simulación se muestran en [fig:7.6] y [fig:7.7]. Los resultados son claros: para el SHO, el delantero Euler no es estable, ni conserva volúmenes de espacio de fase. Sin embargo, Euler simpléctico es estable y también conserva volúmenes de espacio de fase como lo demuestran las dos parcelas.

Resumen del capítulo

Estos son los puntos importantes que se hacen en este capítulo:

• Los integradores de ODE de propósito general generalmente no conservan energía. Por lo tanto, son inapropiados para problemas donde la conservación de energía es importante, como la simulación de movimiento en el espacio.
• Los integradores Symplectic son solucionadores especializados que se utilizan exactamente para aquellas situaciones en las que es importante que el solucionador ODE garantice la conservación de energía. Son particularmente comunes en el cálculo de las trayectorias de los objetos en el espacio.
• La conservación de energía en los sistemas mecánicos se entiende mejor en el contexto de la mecánica hamiltoniana, que es una generalización de la mecánica newtoniana que probablemente aprendiste en tus clases introductorias de física.
• Además de conservar energía, un sistema simpléctico también conserva volúmenes de espacio de fase. Este hecho es conocido como “teorema de Liouville”. Un integrador simpléctico conservará los volúmenes de espacio de fase como demostramos para el SHO, tanto a través de métodos analíticos como de simulación utilizando el método simpléctico de Euler.