20.7: Área de triángulos sólidos

Teorema\(\PageIndex{1}\)

Dejar\(a=BC\) y\(h_A\) ser la altitud desde\(A\) adentro\(\triangle ABC\). Entonces

\(\text{area }(\blacktriangle ABC)=\tfrac12\cdot a\cdot h_A.\)

Prueba

Dibuja la línea\(m\) a través\(A\) que es paralela\((BC)\) y la línea a\(n\) través de\(C\) paralela a\((AB)\). Tenga en cuenta que las líneas\(m\) y no\(n\) son paralelas; denotan por\(D\) su punto de intersección. Por construcción,\(\square ABCD\) es un paralelogramo.

Tenga en cuenta que\(\blacksquare ABCD\) admite una subdivisión en\(\blacktriangle ABC\) y\(\blacktriangle CDA\). Por lo tanto,\[\text{area }(\blacksquare ABCD) = \text{area }(\blacktriangle ABC) + \text{area }(\blacktriangle CDA)\]

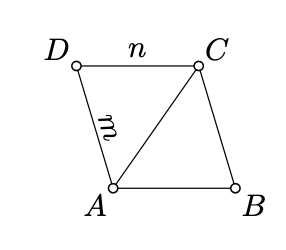
Dado que\(\square ABCD\) es un paralelogramo, Lemma 7.5.1 implica que

\(AB=CD \quad \text{and} \quad BC=DA.\)

Por lo tanto, por la condición de congruencia SSS, tenemos\(\triangle ABC\cong\triangle CDA\). En particular

\(\text{area }(\blacktriangle ABC) = \text{area }(\blacktriangle CDA).\)

De arriba y de la Proposición 20.6.1, obtenemos que

\(\begin{aligned} \text{area }(\blacktriangle ABC) &=\tfrac12\cdot\text{area }(\blacksquare ABCD)= \\ &=\tfrac12\cdot h_A\cdot a\end{aligned}\)

Ejercicio\(\PageIndex{1}\)

Dejar\(h_A\),\(h_B\), y\(h_C\) denotar las altitudes de\(\triangle ABC\) desde vértices\(A\),\(B\) y\(C\) respectivamente. Tenga en cuenta que del teorema\(\PageIndex{1}\), se deduce que

\(h_A\cdot BC=h_B\cdot CA=h_C\cdot AB.\)

Dar una prueba de esta declaración sin usar área.

Insinuación

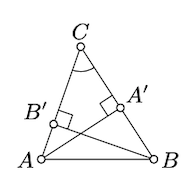
Sin pérdida de generalidad, podemos suponer que los ángulos\(ABC\) y\(BCA\) son agudos.

Dejar\(A'\) y\(B'\) denotar los puntos del pie de\(A\) y\(B\) sobre\((BC)\) y\((AC)\) respectivamente. Tenga en cuenta que\(h_A = AA'\) y\(h_B = BB'\).

Tenga en cuenta que\(\triangle AA'C \sim \triangle BB'C\); de hecho el ángulo a\(C\) es compartido y los ángulos en\(A'\) y\(B'\) son correctos. En particular\(\dfrac{AA'}{BB'} = \dfrac{AC}{BC}\) o, de manera equivalente,\(h_A \cdot BC = h_B \cdot AC\).

Ejercicio\(\PageIndex{2}\)

Supongamos que\(M\) se encuentra dentro del paralelogramo\(ABCD\); es decir,\(M\) pertenece al paralelogramo sólido\(\blacksquare ABCD\), pero no se encuentra en sus lados. Demostrar que

\(\text{area }(\blacktriangle ABM)+\text{area }(\blacktriangle CDM) =\tfrac12\cdot \text{area }(\blacksquare ABCD).\)

Insinuación

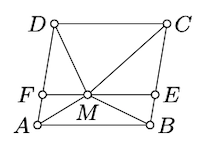
Dibuja la\(\ell\) línea\(M\) paralela a\([AB]\) y\([CD]\); se\(\blacksquare ABCD\) subdivide en dos paralelogramos sólidos que se denotarán por\(\blacksquare ABEF\) y\(\blacksquare CDFE\). En particular,

\(\text{area } (\blacksquare ABCD) = \text{area } (\blacksquare ABEF) + \text{area } (\blacksquare CDFE)\).

Por la Proposición 20.6.1 y Teorema\(\PageIndex{1}\) obtenemos que

\(\begin{array} {l} {\text{area } (\blacktriangle ABM) = \dfrac{1}{2} \cdot \text{area } (\blacksquare ABEF),} \\ {\text{area } (\blacktriangle CDM) = \dfrac{1}{2} \cdot \text{area } (\blacksquare CDFE)} \end{array}\)

y de ahí el resultado.

Ejercicio\(\PageIndex{3}\)

Supongamos que las diagonales de un cuadriángulo no degenerado se\(ABCD\) cruzan en el punto\(M\). Demostrar que

\(\text{area }(\blacktriangle ABM)\cdot\text{area }(\blacktriangle CDM) = \text{area }(\blacktriangle BCM)\cdot\text{area }(\blacktriangle DAM).\)

Insinuación

Dejar\(h_A\) y\(h_C\) denotar las distancias desde\(A\) y\(C\) hacia la línea\((BD)\) respectivamente. Según el teorema\(\PageIndex{1}\),

\(\text{area }(\blacktriangle ABM) = \dfrac{1}{2} \cdot h_A \cdot BM\);\(\text{area }(\blacktriangle BCM) = \dfrac{1}{2} \cdot h_C \cdot BM\);
\(\text{area }(\blacktriangle CDM) = \dfrac{1}{2} \cdot h_C \cdot DM\);\(\text{area }(\blacktriangle ABM) = \dfrac{1}{2} \cdot h_A \cdot DM\).

Por lo tanto

\(\begin{array} {rcl} {\text{area } (\blacktriangle ABM) \cdot \text{area } (\blacktriangle CDM)} & = & {\dfrac{1}{4} \cdot h_A \cdot h_C \cdot DM \cdot BM =} \\ {} & = & {\text{area } (\blacktriangle BCM) \cdot \text{area } (\blacktriangle DAM)} \end{array}\)

Ejercicio\(\PageIndex{4}\)

\(r\)Sea el inradio de\(\triangle ABC\) y\(p\) sea su semiperímetro; es decir,\(p=\tfrac12\cdot(AB+BC+CA)\). Demostrar que

\(\text{area }(\blacktriangle ABC)=p\cdot r.\)

Insinuación

\(I\)Déjese ser el incenter de\(\triangle ABC\). Tenga en cuenta que se\(\blacktriangle ABC\) puede subdividir en\(\blacktriangle IAB, \blacktriangle IBC\) y\(\blacktriangle ICA\).

Queda por aplicar el Teorema\(\PageIndex{1}\) a cada uno de estos triángulos y resumir los resultados.

Ejercicio\(\PageIndex{5}\)

Mostrar que cualquier conjunto poligonal admite una subdivisión en una colección finita de triángulos sólidos y un conjunto degenerado. Concluimos que para cualquier conjunto poligonal, su área está definida de manera única.

Insinuación

Fijar un conjunto poligonal\(\mathcal{P}\). Sin pérdida de generalidad podemos suponer que\(\mathcal{P}\) es una unión de una colección finita de triángulos sólidos. Corta\(\mathcal{P}\) a lo largo de las extensiones de los lados de todos los triángulos, se\(\mathcal{P}\) subdivide en polígonos convexos. Cortar cada polígono por diagonales de un vértice produce una subdivisión en triángulos sólidos.