20.6: Área de paralelogramos sólidos

Última actualización
Guardar como PDF

Page ID: 114509

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Teorema$\PageIndex{1}$

Dejar$\square ABCD$ ser un paralelogramo en el plano euclidiano,$a=AB$ y$h$ ser la distancia entre las líneas$(AB)$ y$(CD)$. Entonces

$\text{area }(\blacksquare ABCD)=a\cdot h.$

$2021-03-03 9.01.52.png$

Prueba

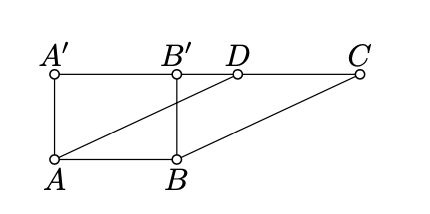
Dejar$A'$ y$B'$ denotar los puntos del pie de$A$ y$B$ en la línea$(CD)$.

Tenga en cuenta que$ABB'A'$ es un rectángulo con lados$a$ y$h$. Por Teorema 20.5.1,

\[\text{area }(\blacksquare ABB'A')=h\cdot a.\]

Sin pérdida de generalidad, podemos suponer que$\blacksquare ABCA'$ contiene$\blacksquare ABCD$ y$\blacksquare ABB'A'$. En este caso$\blacksquare ABCA'$ admite dos subdivisiones:

$\blacksquare ABCA'=\blacksquare ABCD\cup\blacktriangle AA'D=\blacksquare ABB'A'\cup\blacksquare BB'C.$

Por la Proposición 20.4.2,

\[\begin{aligned} \text{area }( \blacksquare ABCD)&+\text{area }(\blacktriangle AA'D)= \\ &= \text{area }(\blacksquare ABB'A')+ \text{area } (\blacktriangle BB'C). \end{aligned}\]

Tenga en cuenta que

En efecto, dado que los$ABB'A'$ cuadriláteros y$ABCD$ son paralelogramos, por Lemma 7.5.1, tenemos eso$AA'=BB'$,$AD=BC$, y$DC=AB=A'B'$. De ello se deduce que$A'D=B'C$. Aplicando la condición de congruencia SSS, obtenemos 20.6.3.

En particular,

\[\text{area }(\blacktriangle BB'C)=\text{area } (\blacktriangle AA'D). \]

Restar 20.6.4 de 20.4.2, obtenemos que

\[\text{area } (\blacksquare ABCD)=\text{area }(\blacksquare ABB'D).\]

Queda por aplicar 20.6.1.

Ejercicio$\PageIndex{1}$

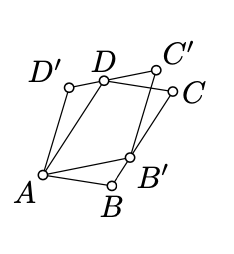
Supongamos$\square ABCD$ y$\square AB'C'D'$ son dos paralelogramos tales que$B'\in[BC]$ y$D\in [C'D']$. Demostrar que

$\text{area }(\blacksquare ABCD)=\text{area }(\blacksquare AB'C'D').$

$2021-03-03 9.02.53.png$

Pista

Supongamos que$E$ denota el punto de intersección de las líneas$(BC)$ y$(C'D')$.

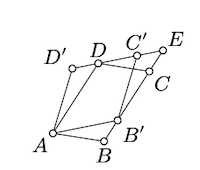
$2021-03-03 9.09.22.png$

Utilice Proposición$\PageIndex{1}$ para probar las dos identidades siguientes:

$\begin{array} {l} {\text{area } (\blacksquare AB'ED) = \text{area } (\blacksquare ABCD),} \\ {\text{area } (\blacksquare AB'ED) = \text{area } (\blacksquare AB'C'D')} \end{array}$