20.8: Método de área
- Page ID
- 114490
En esta sección daremos ejemplos de pruebas delgadas utilizando las propiedades del área. Tenga en cuenta que estas pruebas no son realmente elementales ya que el precio que se paga para introducir la función de área es alto.
Comenzamos con la prueba del teorema de Pitágoras. En los Elementos de Euclides, el teorema de Pitágoras se formuló como igualdad 20.8.1 a continuación y la prueba utilizó una técnica similar.
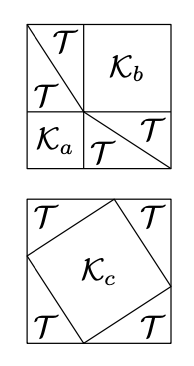
Comprobante. Tenemos que demostrar que si\(a\) y\(b\) son piernas y\(c\) es la hipotenusa de un triángulo rectángulo, entonces
\(a^2+b^2=c^2.\)
Supongamos que\(\mathcal{T}\) denota el triángulo recto sólido con patas\(a\)\(b\) y y\(\mathcal{K}_{x}\) el cuadrado sólido con lado\(x\).
Construyamos dos subdivisiones de\(\mathcal{K}_{a+b}\):
- \(\mathcal{K}_{a+b}\)Subdividir en dos cuadrados sólidos congruentes con\(\mathcal{K}_a\) y\(\mathcal{K}_b\) y 4 triángulos sólidos congruentes con\(\mathcal{T}\), ver el primer diagrama.
- \(\mathcal{K}_{a+b}\)Subdividir en un cuadrado sólido congruente\(\mathcal{K}_c\) y 4 triángulos rectos sólidos congruentes con\(\mathcal{T}\), ver el segundo diagrama.
Aplicando la Proposición 20.4.2 pocas veces, lo conseguimos
\(\begin{aligned} \text{area }\mathcal{K}_{a+b} &= \text{area }\mathcal{K}_{a}+\text{area } \mathcal{K}_{b} +4\cdot\text{area }\mathcal{T}= \\ &=\text{area }\mathcal{K}_{c}+4\cdot\text{area }\mathcal{T}.\end{aligned}\)
Por lo tanto,
\[\text{area }\mathcal{K}_{a}+\text{area }\mathcal{K}_{b}=\text{area }\mathcal{K}_{c}.\]
Por Teorema 20.5.1,
\(\text{area }\mathcal{K}_x=x^2,\)
para cualquier\(x>0\). De ahí sigue el enunciado.
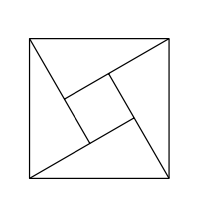
Construir otra prueba del teorema de Pitágoras basada en el diagrama.
(En las anotaciones anteriores se muestra una subdivisión de\(\mathcal{K}_c\) en\(\mathcal{K}_{a-b}\) y cuatro copias de\(\mathcal{T}\) if\(a>b\).)
- Pista
-
Suponiendo\(a > b\),\(\mathcal{Q}_c\) subdividimos en\(\mathcal{Q}_{a - b}\) y cuatro triángulos congruentes a\(\mathcal{T}\). Por lo tanto
\[\text{area } \mathcal{Q}_c = \text{area } \mathcal{Q}_{a - b} + 4 \cdot \text{area } \mathcal{T}.\]
Según el Teorema 20.7.1,\(\text{area } \mathcal{T} = \tfrac{1}{2} \cdot a \cdot b\). Por lo tanto, la identidad 20.8.2 puede escribirse como
\(c^2 = (a - b)^2 + 2 \cdot a \cdot b.\)
Simplificando, obtenemos el teorema de Pitágoras.
El caso\(a = b\) es aún más sencillo. El caso se\(b > a\) puede hacer de la misma manera.
Mostrar que la suma de distancias desde un punto a los lados de un triángulo equilátero es la misma para todos los puntos dentro del triángulo.
- Pista
-
Si\(X\) es un punto dentro de\(\triangle ABC\), entonces\(\blacktriangle ABC\) se subdivide en\(\blacktriangle ABX\),\(\blacktriangle BCX\), y\(\blacktriangle CAX\). Por lo tanto
\(\text{area } (\blacktriangle ABX) + \text{area } (\blacktriangle BCX) + \text{area } (\blacktriangle CAX) = \text{area } (\blacktriangle ABC).\)
Set\(a = AB = BC = CA\). Dejar\(h_1, h_2\), y\(h_3\) denotar las distancias de\(X\) a los lados\([AB]\),\([BC]\), y\([CA]\). Entonces por el Teorema 20.7.1,
\(\text{area } (\blacktriangle ABX) = \dfrac{1}{2} \cdot h_1 \cdot a\),\(\text{area } (\blacktriangle BCX) = \dfrac{1}{2} \cdot h_2 \cdot a\),\(\text{area } (\blacktriangle CAX) = \dfrac{1}{2} \cdot h_3 \cdot a\).
Por lo tanto,
\(h_1 + h_2 + h_3 = \dfrac{2}{a} \cdot \text{area } (\blacktriangle ABC).\)
Supongamos que dos triángulos\(ABC\) y\(A'B'C'\) en el plano euclidiano tienen altitudes iguales caídas desde\(A\) y\(A'\) respectivamente. Entonces
\[\dfrac{\text{area }(\blacktriangle A'B'C')}{\text{area }(\blacktriangle ABC)} = \dfrac{B'C'}{BC}.\]
En particular, la misma identidad sostiene si\(A=A'\) y las bases\([BC]\) y\([B'C']\) se encuentran en una línea.
- Prueba
-
Deja que\(h\) sea la altitud. Por Teorema 20.7.1,
\(\dfrac{\text{area }(\blacktriangle A'B'C')}{\text{area }(\blacktriangle ABC)} = \dfrac{\frac12 \cdot h\cdot B'C'}{\frac12 \cdot h\cdot BC} = \dfrac{B'C'}{BC}.\)
Ahora vamos a mostrar cómo usar esta afirmación para probar Lemma 8.4.1. Primero, recordemos su declaración:
Si no\(\triangle ABC\) es degenerado y su ángulo bisectriz en las\(A\) intersectas\([BC]\) y el punto\(D\). Entonces
\(\dfrac{AB}{AC} =\dfrac{DB}{DC}.\)
- Prueba
-
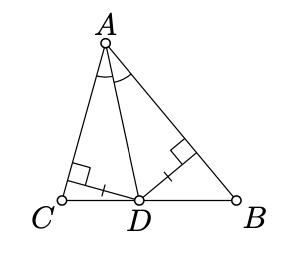
Aplicando Reclamación\(\PageIndex{1}\), lo conseguimos
\(\dfrac{\text{area } (\blacktriangle ABD)}{\text{area } (\blacktriangle ACD)} = \dfrac{BD}{CD}.\)
Por Proposición 8.10 los triángulos\(ABD\) y\(ACD\) tienen altitudes iguales desde\(D\). Aplicando Reclamación de\(\PageIndex{1}\) nuevo, lo conseguimos
\(\dfrac{\text{area } (\blacktriangle ABD)}{\text{area } (\blacktriangle ACD)} = \dfrac{AB}{AC}.\)
y de ahí el resultado.
Supongamos que\(ABC\) es un triángulo no degenerado y\(A'\) se encuentra entre\(B\) y\(C\). En este caso el segmento de línea\([AA']\) se llama ceviano (lleva el nombre de Giovanni Ceva y se pronuncia como cheviano.) de\(\triangle ABC\) at\(A\). El segundo enunciado en el siguiente ejercicio se denomina teorema de Ceva.
Dejar\(ABC\) ser un triángulo no degenerado. Supongamos sus cevianos\([AA']\),\([BB']\) y se\([CC']\) cruzan en un punto\(X\). Demostrar que
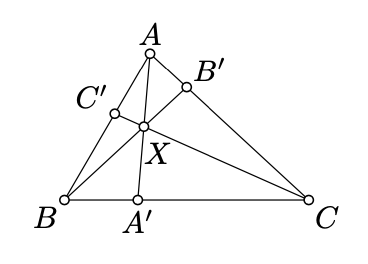
\(\begin{aligned} \frac{\text{area }(\blacktriangle ABX)}{\text{area }(\blacktriangle BCX)}&=\frac{AB'}{B'C}, \\ \frac{\text{area }(\blacktriangle BCX)}{\text{area }(\blacktriangle CAX)}&=\frac{BC'}{C'A}, \\ \frac{\text{area }(\blacktriangle CAX)}{\text{area }(\blacktriangle ABX)}&=\frac{CA'}{A'B} .\end{aligned}\)
Concluir que
\(\dfrac{AB'\cdot CA'\cdot BC'}{B'C\cdot A'B\cdot C'A}=1.\)
- Pista
-
Aplicar Reclamación\(\PageIndex{1}\) para demostrar que
\(\dfrac{\text{area } (\blacktriangle ABB')}{\text{area } (\blacktriangle BCB')} = \dfrac{\text{area } (\blacktriangle AXB')}{\text{area } (\blacktriangle XCB')} = \dfrac{AB'}{B'C}\).
Y observa que
\(\text{area } (\blacktriangle ABB') = \text{area } (\blacktriangle ABX) + \text{area } (\blacktriangle AXB')\),
\(\text{area } (\blacktriangle BCB') = \text{area } (\blacktriangle BCX) + \text{area } (\blacktriangle XCB')\).Implica la primera identidad; el resto es análogo.
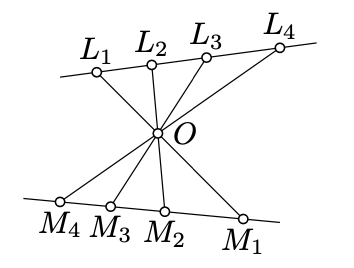
Supongamos que los puntos\(L_1\)\(L_2\),\(L_3\),,\(L_4\) se encuentran en una línea\(\ell\) y los puntos\(M_1\)\(M_2\),,\(M_3\),\(M_4\) se encuentran en una línea \(m\). Supongamos que las líneas\((L_1M_1)\)\((L_2M_2)\),\((L_3M_3)\),, y\((L_4M_4)\) pasan por un punto\(O\) que no se encuentra sobre\(\ell\) ni\(m\).
- Aplicar Reclamación\(\PageIndex{1}\) para demostrar eso\[\frac{\text{area }\blacktriangle OL_iL_j}{\text{area }\blacktriangle OM_iM_j}=\frac{OL_i\cdot OL_j}{OM_i\cdot OM_j}\] para cualquier\(i\ne j\).
- Utilizar (a) para demostrar\[\frac{L_1L_2\cdot L_3L_4}{L_2L_3\cdot L_4L_1}=\frac{M_1M_2\cdot M_3M_4}{M_2M_3\cdot M_4M_1};\] que es decir, los cuatriples\((L_1, L_2, L_3, L_4)\) y\((M_1, M_2, M_3, M_4)\) tienen la misma relación cruzada.
- Pista
-
Para probar (a), aplicar Reclamar\(\PageIndex{1}\) dos veces a los triángulos\(OL_iL_j, OL_jM_i\), y\(OM_iM_j\).
Para probar la parte (b), use\(\PageIndex{1}\) Reclamar para reescribir el lado izquierdo usando las áreas de triángulos\(OL_1L_2, OL_2L_3, OL_3L_4\), y\(OL_4L_1\). Además, use la parte (a) para reescribirla usando áreas de\(OM_1M_2, OM_2M_3,OM_3M_4\),\(OM_4M_1\) y aplique Reclamar\(\PageIndex{1}\) nuevamente para obtener el lado derecho.