1.1: Introducción a los Elementos de Euclides

Última actualización
Guardar como PDF

Page ID: 118030

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Como introducción, cubriremos solo las Proposiciones 1-28 del Libro 1. Esta es una introducción a la geometría neutra o absoluta que subsume tanto la geometría euclidiana como la hiperbólica. El sitio web dado es la traducción de Sir Thomas L. Heath y su comentario muy informativo; es decir, el (¡barato!) Libros Dover en formato electrónico. Al hacer clic en el número de proposición, aparece el enunciado y su prueba histórica. A modo de ejemplo, aquí está la Proposición 5 el famoso Pons Asinorum (Puente de Asses), un doble sentido desde su forma y “honrando” a esos burros que no pueden cruzarlo (se entiende la idea). Todo el camino de regreso a los griegos, la geometría basada en pruebas separaba a los cognoscenti del plebeyo. Aunque se usa aquí, intentaremos evitar identificar segmentos o ángulos de línea del mismo tamaño como “iguales” porque también son conjuntos de puntos y se definen dos conjuntos para ser iguales si contienen exactamente los mismos elementos. Congruente es la palabra que habitualmente usaremos o el término igual en medida, esa “medida” teórica de perfección que nunca se puede lograr midiendo, pero muchos grandes geometros han utilizado el término “igual” en este contexto. Por favor, no.

Proposición 5

En los triángulos isósceles, los ángulos en la base son iguales entre sí, y, si las líneas rectas iguales se producen más, los ángulos debajo de la base serán iguales entre sí.

Prueba: Dejar$\Delta ABC$ ser un triángulo isósceles que tenga el lado$\overline{AB}$ igual al lado$\overline{AC}$; y dejar que las líneas rectas$\overleftrightarrow{BD},$$\overleftrightarrow{CE}$ se produzcan más en línea recta con$\overline{AB}$,$\overline{AC}$. [Post. 2]

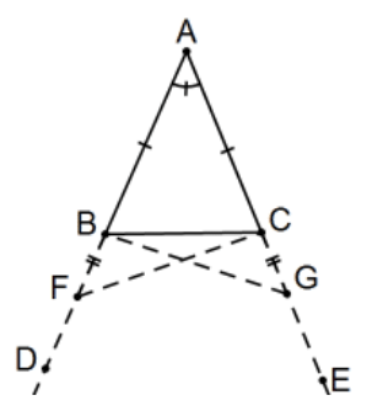
$Captura de pantalla 2022-06-23 en 10.52.40 AM.png$

Yo digo que el ángulo$\angle ABC$ es igual al ángulo$\angle ACB$, y el ángulo$\angle CBD$ al ángulo$\angle BCE.$

Que$F$ se tome un punto al azar encendido$\mathrm{BD}$; de$\mathrm{AE}$ lo mayor$[\mathrm{AE}>\mathrm{AD}$] dejar que AG se corte igual a AF cuanto menos; y dejar que se unan las líneas rectas FC, GB. [Post. 1]

Entonces, dado que$\mathrm{AF}$ es igual$\mathrm{AB}$ a$\mathrm{AG}$ y a$\mathrm{AC}$, los dos lados$\mathrm{FA}, \mathrm{AC}$ son iguales a los dos lados$\mathrm{GA}$$\mathrm{AB}$, respectivamente; y contienen un ángulo común, el ángulo FAG.

Por lo tanto, la base FC es igual a la base GB, y el triángulo AFC es igual al triángulo AGB, y los ángulos restantes serán iguales a los ángulos restantes respectivamente, es decir, aquellos que subtienden los lados iguales, es decir, el ángulo ACF al ángulo ABG, y el ángulo AFC al ángulo AGB.

Y, ya que el todo$\mathrm{AF}$ es igual al todo$\mathrm{AG}$, y en estos$\mathrm{AB}$ es igual a$\mathrm{AC}$, el resto$\mathrm{BF}$ es igual al resto CG.

Pero FC también se demostró igual a GB; por lo tanto los dos lados$\mathrm{BF}, \mathrm{FC}$ son iguales a los dos lados CG, GB respectivamente; y el ángulo BFC es igual al ángulo CGB, mientras que la base$\mathrm{BC}$ es común a ellos; por lo tanto el triángulo BFC también es igual al triángulo CGB, y el restante serán iguales a los ángulos restantes respectivamente, es decir, aquellos que subtienden los lados iguales; por lo tanto, el ángulo FBC es igual al ángulo GCB, y el ángulo BCF al ángulo CBG.

En consecuencia, dado que todo el ángulo ABG se demostró igual al ángulo ACF, y en estos el ángulo CBG es igual al ángulo BCF, el ángulo restante$\mathrm{ABC}$ es igual al ángulo restante ACB; y están en la base del triángulo ABC. Pero el ángulo FBC también se demostró igual al ángulo GCB; y están debajo de la base.

QED.

[Quod Erat Demostrandum, latín para “lo que iba a demostrarse”.]

Nota

QEF es otro pero menos común, “Quod Erat Faciendum “, lo que se debía haber hecho”. ¿Hay pruebas más fáciles? ¡Por supuesto, vimos varios en la Introducción! Pero no podemos empezar por ningún lado. ¿Por qué, por ejemplo, comenzar con la Prop 5? En parte, porque el comienzo de los Elementos es un poco tembloroso y sólo lo vamos a “arreglar” en parte. Si dedicaramos demasiado tiempo a un enfoque moderno, no iríamos más allá de eso.

Colaboradores

http://aleph0.clarku.edu/ djoyce/java/elements/bookI/bookI.html - Usado con permiso del propietario. [O simplemente Google “Euclid Book 1" si esta URL (y sitio muy útil) deja de estar disponible. Por ejemplo: http://www.perseus.tufts.edu/hopper/text?doc=Euc.+1]