1.2: Definiciones del libro 1

1. Un punto es aquello que no tiene parte. [Esencialmente sin sentido como definición. Desde una perspectiva moderna, debe haber algunos términos indefinidos. Esta es una.]
2. Una línea es de longitud sin ancho. [Nuevamente, esta no es una definición. Es otro término indefinido.]
3. Las extremidades de una línea son puntos. [Puntos finales. Formalmente, algo sobre “entremedias”.]
4. Una línea recta es una línea que se encuentra uniformemente con los puntos sobre sí misma. [¿Decir qué? Las curvas son “líneas” aquí pero ¿qué es “recta”? En el Capítulo 5, lo definiremos formalmente pero ¡no parecerá natural!]
5. Una superficie es aquella que solo tiene longitud y anchura. [Una región en la geometría (plano).]
6. Las extremidades de una superficie son líneas. [Los bordes de un polígono o poliedro son segmentos de línea.]
7. Una superficie plana es una superficie que se encuentra uniformemente con las líneas rectas sobre sí misma. [Ver lo anterior.]
8. Un ángulo plano es la inclinación entre sí de dos líneas en un plano que se encuentran entre sí y no se encuentran en línea recta. [¿Moderno? Un ángulo es la unión de dos rayos con un punto inicial común.]
9. Y cuando las líneas que contienen el ángulo son rectas, el ángulo se llama rectilineal. [A diferencia de un ángulo determinado por la intersección de dos curvas “suaves”; es decir, la intersección de sus tangentes en el punto de intersección. Los necesitaremos en el “modelo de disco de Poincaré” para la geometría hiperbólica.]
10. Cuando una línea recta establecida en una línea recta hace que los ángulos adyacentes sean iguales entre sí, cada uno de los ángulos iguales es recto, y la línea recta que se encuentra sobre la otra se llama perpendicular a aquella sobre la que se encuentra. [¿Moderno? Las líneas perpendiculares son líneas que se cruzan para formar ángulos congruentes y adyacentes. Los ángulos que forman se llaman ángulos rectos.]
11. Un ángulo obtuso es un ángulo mayor que un ángulo recto. [Una definición real.]
12. Un ángulo agudo es un ángulo menor que un ángulo recto. [¡Dos seguidos!]
13. Un límite es aquello que es una extremidad de cualquier cosa. [¿Tu sarcasmo aquí?]
14. Una figura es aquella que está contenida por cualquier límite o límites. [Es decir, cerrado y acotado.]
15. Un círculo es una figura plana contenida por una línea [curva] tal que todas las líneas rectas que caen sobre él desde un punto entre las que se encuentran dentro de la figura son iguales entre sí. [Otro, “¿Qué decir?”!]
16. Y al punto se le llama el centro del círculo. [¡Otra definición real!]
17. Un diámetro del círculo es cualquier línea recta dibujada a través del centro y terminada en ambas direcciones por la circunferencia del círculo, y tal línea recta también biseca el círculo. [Omitir “circunferencia”.]
18. Un semicírculo es la figura contenida por el diámetro y la circunferencia cortada por él. Y el centro del semicírculo es el mismo que el del círculo. [Como en #17, “circunferencia” implica el círculo mismo, el conjunto de puntos equidistantes de un punto dado; circunferencia en realidad significa la medida lineal del círculo.]
19. Las figuras rectilíneas son las que están contenidas por líneas rectas, siendo las figuras trilaterales las contenidas por tres, las cuadriláteras las contenidas por cuatro, y las multilaterales las contenidas por más de cuatro líneas rectas. [Definiciones reales pero diríamos polígono y, en caso de tres, triángulo, pero trilateral se usa como es cuadrilátero y\(n\) -gon si queremos especificar el número de lados,\(n .]\)
20. De las figuras trilaterales, un triángulo equilátero es aquel que tiene sus tres lados iguales, un triángulo isósceles el que tiene dos de sus lados solos iguales, y un triángulo escaleno el que tiene sus tres lados desiguales.
21. Además, de las figuras trilaterales, un triángulo en ángulo recto es aquel que tiene un ángulo recto, un triángulo obtuso que tiene un ángulo obtuso, y un triángulo en ángulo agudo el que tiene sus tres ángulos agudos. [Para nosotros, triángulo rectángulo, triángulo obtuso y triángulo agudo.]
22. De figuras cuadriláteras, un cuadrado es aquel que es a la vez equilátero y en ángulo recto; un oblongo lo que es de ángulo recto pero no [necesariamente] equilátero; un rombo lo que es equilátero pero no [necesariamente] en ángulo recto; y un romboide lo que tiene su lados opuestos y ángulos iguales entre sí pero no es ni equilátero ni en ángulo recto. Y que los cuadriláteros distintos a estos se llamen trapecios. [¡Nunca se usó!]
23. Las líneas rectas paralelas son líneas rectas que, estando en el mismo plano y produciéndose indefinidamente en ambas direcciones, no se encuentran entre sí en ninguna dirección. [¿Existen? Sí (pero no en geometría elíptica), pero ¿qué significa “infinito”? Formalmente, es la Propiedad de Arquímedes: Dados dos segmentos, suficientes copias del más corto supera al más largo (independientemente de sus longitudes.]

Postulados. [Axioma y postulado son términos intercambiables desde la perspectiva moderna, declaraciones aceptadas como verdaderas sin pruebas. No en algún sentido universal, sólo en el contexto que se examina]

Que se postule lo siguiente:

1. Dibujar una línea recta desde cualquier punto a cualquier punto. [En adelante, Axioma 1: Dos puntos determinan...]
2. Producir una línea recta finita de forma continua en línea recta. [Las líneas son “infinitas” - Subsumidos bajo el Postulado Gobernante]
3. Describir un círculo con cualquier centro y distancia. [Axiomáticamente, un punto y un radio determinan un círculo único y los círculos se comportan como deberían”, dijo Nuff.]
4. Que todos los ángulos rectos son iguales entre sí. [Subsumido bajo el Postulado Transtractor.]
5. Eso, si una línea recta que cae sobre dos líneas rectas hace que los ángulos interiores del mismo lado sean menores que dos ángulos rectos, las dos líneas rectas, si se producen indefinidamente, se encuentran en ese lado en el que están los ángulos menores que los dos ángulos rectos. [5º Postulado de Euclides, forma tradicional. Mucho más común es la forma de Playfair: Dada una línea y un punto no en la línea, hay como máximo una línea en el punto dado que es paralela a la línea dada. ¿A lo sumo uno? Tal vez ni siquiera uno?! No, sino por prueba, no por axioma].

Nociones comunes [Desde una perspectiva moderna, estas se derivan de la teoría de conjuntos y de las propiedades de los números reales que también se pueden desarrollar axiomáticamente. Si lo hiciéramos, ¡nunca terminaríamos!]

1. Las cosas que son iguales a lo mismo también son iguales entre sí. [Lee: La congruencia es transitiva.]
2. Si se agregan iguales a iguales, los enteros son iguales.
3. Si se restan iguales de iguales, los restos son iguales.
4. Las cosas que coinciden entre sí son iguales entre sí.
5. El conjunto es mayor que la parte.

Proposición 1. En una línea recta finita dada para construir un triángulo equilátero.

[Observe el uso del infinitivo como comando, “para construir”. Piensa en el latín antiguo (o español moderno). También “línea recta finita” significa segmento de línea.]

Construcción: Elija cualquiera de 2 puntos en la línea, digamos A y B. Sea C la intersección de los círculos (A; AB) y (B; AB), los círculos centrados en\(A\) y\(B\) ambos de radio\(\mathrm{AB}\) (solo una de las dos intersecciones de estos dos círculos para ser más precisos). El triángulo determinado por los 3 puntos,\(\triangle \mathrm{ABC}\) es equilátero.

Prueba: Por construcción, los 3 lados son congruentes, la definición de equilátero. [Pero, ¿cómo sabemos que los círculos tienen que cruzarse? ¿Pueden “deslizarse” entre sí sin cruzarse? No, pero hay geometrías donde podrían. Sin molestarnos en expresarlos, asumimos (como hicieron los griegos) que nuestros axiomas aseguran la validez de tales consideraciones de “continuidad”.]

Proposición 2. Colocar en un punto dado (como una extremidad) una línea recta igual a una línea recta dada

Como se dijo, esto realmente significa “construir”; es decir, usar una brújula para copiar un segmento de línea en cualquier punto de otra línea. Es inmediato del Postulado Gobernante; exactamente un punto (con dirección) para cualquier longitud dada.

Proposición 3. Dadas dos líneas rectas desiguales, para cortar de lo mayor una línea recta igual a la menor. [Esto también forma parte del Postulado Gobernante así que nada que probar, al menos desde un punto de vista moderno.]

Proposición 4. Si dos triángulos tienen los dos lados iguales a dos lados respectivamente, y tienen iguales los ángulos contenidos por las líneas rectas iguales, también tendrán la base igual a la base, el triángulo será igual al triángulo, y los ángulos restantes serán iguales a los ángulos restantes respectivamente, a saber los que subtienden los lados iguales. [Es decir, Side-Angle-Side (SAS) que asumiremos como nuestro axioma de congruencia triangular. Se prueba en el Libro 1 pero la “superposición”, la suposición subyacente de la prueba griega antigua, es tentadoramente obvia así que no culpes demasiado a los griegos por no darse cuenta de la necesidad de un axioma; en nuestro caso, el Axioma SAS. ]

Proposición 5. En los triángulos isósceles, los ángulos en la base son iguales entre sí, y, si las líneas rectas iguales se producen más, los ángulos debajo de la base serán iguales entre sí.

[Consulte la Introducción y la introducción a este capítulo y diga “los ángulos de base son congruentes"].

Proposición 6. Si en un triángulo dos ángulos son iguales entre sí, los lados que subtienden los ángulos iguales también serán iguales entre sí. [Lo contrario de los “ángulos base de un teorema de triángulo isósceles”; como suele decirse: En un triángulo, los lados opuestos a los ángulos congruentes son congruentes.]

Dado:\(\triangle \mathrm{ABC}\) con\(\angle \mathrm{B} \cong \angle \mathrm{C} \underline{\text { Prove: }} \mathrm{AB} \cong \mathrm{AC}\).

Prueba: Tomar D para ser el punto a lo largo del rayo CA con\(C D \cong B A\) (por el Postulado Gobernante). Ahora\(\triangle \mathrm{DCB} \cong \triangle \mathrm{ABC}\) por SAS así\(\angle \mathrm{DBC} \cong \angle \mathrm{ACB}\) por cpctc y, por hipótesis y transitividad,\(\angle \mathrm{DBC} \cong \angle \mathrm{ABC}\). Por el Postulado Transportador, rayo\(\mathrm{BD}\) es el mismo rayo que BA así, por el Postulado Gobernante nuevamente,\(\mathrm{D}=\mathrm{A}\) (¡exactamente el mismo punto!) , y\(\mathrm{CA} \cong \mathrm{BA}\) simplemente renombrando\(\mathrm{CD}\) como CA. QED.

Proposición 7. Dadas dos líneas rectas construidas sobre una recta (desde sus extremidades) y reunidas en un punto, no se puede construir sobre la misma línea recta (desde sus extremidades), y en el mismo lado de la misma, otras dos líneas rectas que se encuentran en otro punto e iguales a las dos primeras respectivamente, es decir, cada una a lo que tiene la misma extremidad con él. [Esto, junto con la Prop 8, generalmente se conoce como el Teorema de Congruencia Lateral Lateral (SSS). Formalmente, si dos triángulos tienen tres pares de lados congruentes, los propios triángulos son congruentes.]

Proposición 8 (SSS). Si dos triángulos tienen los dos lados iguales a dos lados respectivamente, y tienen también la base igual a la base, también tendrán los ángulos iguales que están contenidos por las líneas rectas iguales.

Dado:\(\mathrm{AB} \cong \mathrm{EF}, \mathrm{AC} \cong \mathrm{EG}, \mathrm{BC} \cong \mathrm{FG}\)

Demostrar:\(\quad \triangle \mathrm{ABC} \cong \triangle \mathrm{EFG}\)

Prueba: Copia\(\angle \mathrm{A}\) en E pero en el lado opuesto de la línea EF que\(G\) (Postulado Transportador). A lo largo de ese rayo, deje\(C^{\prime}\) ser el punto tal que\(\mathrm{EC}^{\prime} \cong \mathrm{AC}\) así, por la hipótesis y la transitividad dadas,\(\triangle \mathrm{EC}{ }^{\prime} \mathrm{G}\) es isósceles con ángulos de base en\(C^{\prime}\) y\(G\). Además,\(\triangle \mathrm{ABC} \cong \triangle \mathrm{EFC}^{\prime}\) por\(\mathrm{SAS}\) lo que\(\mathrm{FC}^{\prime} \cong \mathrm{BC}\) por cpctc así\(\triangle \mathrm{FGC}{ }^{\prime}\) es también isósceles, también con ángulos de base en\(\mathrm{C}^{\prime}\) y\(\mathrm{G}\). Añadiendo ángulos congruentes, tenemos\(\angle \mathrm{EC}^{\prime} \mathrm{F} \cong \angle \mathrm{EGF}\). Así\(\triangle \mathrm{EFC}{ }^{\prime} \cong \triangle \mathrm{EFG}\) por\(\mathrm{SAS}\) y\(\triangle \mathrm{ABC} \cong \triangle \mathrm{EFG}\) por transitividad. QED.

Mientras se haga lógicamente, no hay nada de magia en seguir el Libro de Elementos 1 de Euclides en su secuencia original y es conveniente mirar la Prop 23 en este punto:

Proposición 23. En una línea recta dada y en un punto sobre ella para construir un ángulo rectilíneo igual a un ángulo rectilíneo dado. [Es decir, copie un ángulo usando la recta y la brújula.]

Construcción: Para copiar\(\angle \mathrm{A}\) en el punto\(\mathrm{X}\) del lado dado, elija cualquier punto\(B \neq A\) en uno de los rayos de\(\angle A\) un uso que como el radio para círculos centrados en\(A\) y en\(\mathrm{X}\) establecer puntos\(\mathrm{C}\) y\(\mathrm{Y}\) y un arco en las proximidades de (aún no determinado\(\mathrm{Z}\)) Construir el círculo con centro en\(\mathrm{Y}\) de radio\(\mathrm{BC}\) para establecer punto\(\mathrm{Z}\). Ray XZ es el ángulo deseado en el punto\(\mathrm{X}\).

Prueba:\(\triangle \mathrm{ABC} \cong \triangle \mathrm{XYZ}\) por\(\mathrm{SSS}\) así\(\angle \mathrm{A} \cong \angle \mathrm{X}\) por cpctc. \(\mathrm{QED} .\)

Proposición 9. Bisecar un ángulo rectilíneo dado.

Construcción: Elija un punto, digamos B, en uno de los rayos del ángulo y determine el punto\(C\) en el otro rayo construyendo el círculo\((A ; A B)\), el círculo con centro A de radio\(A B\). Con longitud\(r>(1 / 2) m(B C)\), construye círculos\((B ; r)\)\((C ; r)\) y deja\(D\) ser su punto de intersección (más alejado de\(A\), como se muestra en la imagen). Ray AD es el ángulo deseado bisectriz. [NO construya (ni siquiera indique) los segmentos BD y CD ni ninguno de esos segmentos punteados en estas construcciones; solo se indican para aclarar la prueba.]

Prueba:\(\triangle \mathrm{ABD} \cong \triangle \mathrm{ACD}\) por\(\mathrm{SSS}\) para que\(\angle \mathrm{BAD} \cong \angle \mathrm{CAD}\) por cpctc y, por definición de ángulo bisectriz, hayamos terminado. [¿Por qué no hasta ahora? De hecho, hay una\(\mathrm{SAS}\) prueba de ello para que se pudiera haber hecho antes de la SSS. ¿Lo puedes ver?]

QED.

Proposición 10. Bisecar una línea recta finita dada. [Es decir, construir el punto medio de un segmento de línea.]

Construcción: [Nota: Esto no dice la bisectriz perpendicular, solo el punto que biseca; es decir, el punto medio. Después de la construcción tradicional, la bisectriz perpendicular del segmento para determinar su punto medio, veremos otro que enfatiza este punto. El problema es que algunos de ustedes dirán “bisectriz perpendicular” cuando sólo se refiere a uno de “perpendicular” o “bisectriz”. Las palabras tienen sentido, así que úselas correcta y de manera significativa.]

Por medio de círculos, de los mismos radios, cada uno mayor que\((1 / 2) \mathrm{m}(A B)\), construir dos puntos, cada uno equidistante de los puntos finales; en este caso,\(A\) y\(B\) son los puntos finales y\(P\) y\(Q\) son los puntos, cada uno equidistante de\(A\) y\(B\). Finalmente, dejó\(M\) ser la intersección de líneas\(A B\) y PQ. [Al igual que en la Prop 9, NO incluya los segmentos discontinuos en la foto, solo la construcción. Ellos sólo están ahí para mayor claridad en la prueba.]

Prueba: Por SSS,\(\triangle \mathrm{APQ} \cong \triangle \mathrm{BPQ}\) para que\(\angle \mathrm{APQ} \cong \angle \mathrm{BPQ}\) por cpctc. [Nota: Más inteligente hubiera sido decir “De la prueba de la Prop 9, tenemos\(\angle \mathrm{APQ} \cong \angle \mathrm{BPQ}\). ¿Lo puedes ver?] En todo caso, ahora tenemos\(\triangle \mathrm{APM}\)\(\cong \triangle \mathrm{BPM}\) por\(\mathrm{SAS}\) lo que\(\mathrm{AM} \cong \mathrm{BM}\) por cpctc y\(\mathrm{M}\) es el punto medio de\(\mathrm{AB}\). QED.

Nota: Una extensión útil de la prueba anterior es:

Teorema: Un punto está en la bisectriz perpendicular de un segmento de línea si y solo si es equidistante de cada uno de sus puntos finales (PS 1, #20).]

[Como prometí, aquí hay una construcción que probablemente no habrías pensado que aún no podemos probar sino solo porque aún no tenemos AAS o congruencia de ángulos verticales. Si lo hiciéramos...

Construcción: Considerar dos pares de círculos con centros A y B de los mismos radios lo suficientemente grandes como para intersectarse en puntos\(\mathrm{P}\) y Q. Dejar\(\mathrm{M}\) ser la intersección de líneas\(\mathrm{AB}\) y\(\mathrm{PQ}\); entonces\(\mathrm{M}\) es la punto deseado.

Prueba:\(\triangle \mathrm{ABQ} \cong \triangle \mathrm{BAP}\) por SSS así\(\angle \mathrm{ABQ} \cong \angle \mathrm{BAP}\) por cpctc. Pero\(\angle \mathrm{ABQ}=\angle \mathrm{MBQ}\) (es decir, exactamente el mismo ángulo) y\(\angle \mathrm{BAP}=\angle \mathrm{MAP}\) con\(\angle A M P \cong \angle B M Q\) porque son ángulos verticales. Ahora\(\triangle A M P \cong \triangle B M Q\) por\(A A S\) y, por cpctc,\(A M \cong B M\) como se desee. QED.]

Proposición 11. Dibujar una línea recta en ángulo recto a una línea recta dada desde un punto dado sobre ella. [Construir una perpendicular en un punto dado en una línea dada. Nota: No utilice la otra intersección de estos dos círculos. ¿Por qué no? ¿PQ es la única perpendicular a la línea en el punto P? Sí. ¿Por qué?]

Prueba: Ver PS 1, #9.

Proposición 12. A una línea recta infinita dada, desde un punto dado que no está sobre ella, dibujar una recta perpendicular. [Construir una perpendicular a una línea a partir de un punto que no esté en la línea. ¿Es la perpendicular a la línea en el punto? Aún no; no hasta después de la Prop 16.]

Prueba: Ver PS 1, #8.

Proposición 13. Si una línea recta [rayo] configurado en una línea recta hace ángulos, hará dos ángulos rectos o ángulos iguales a dos ángulos rectos. [Nada que probar; es axiomático por el Postulado Transtractor.]

Proposición 14. Si con alguna línea recta, y en un punto sobre ella, dos líneas rectas que no se encuentran del mismo lado hacen que los ángulos adyacentes sean iguales a dos ángulos rectos, las dos líneas rectas estarán en línea recta entre sí. [Aquí tampoco. También es consecuencia del Postulado Transtractor.]

Proposición 15. Si dos líneas rectas se cortan entre sí, hacen que los ángulos verticales sean iguales entre sí.

Prueba: Visto de manera más simple:\(\alpha+\beta=180^{\circ}=\beta+\gamma\) lo que implica\(\alpha=\gamma . \quad\) QED.

Proposición 16. [Teorema de ángulo exterior (forma de geometría neutra). ¡CONÓCELO!] En cualquier triángulo, si se produce uno de los lados, el ángulo exterior es mayor que cualquiera de los ángulos interiores no adyacentes.

Prueba: Deje que el rayo BM sea la mediana en\(\mathrm{B}\) [\(\mathrm{M}\)es el punto medio del segmento AC] y dejar\(\mathrm{E}\) estar a lo largo de ese rayo tal que\(\mathrm{EM} \cong \mathrm{BM}\). Concluir eso\(\angle \mathrm{A} \cong \angle \mathrm{ACE}<\angle \mathrm{ACD}\). ¿Por qué esto prueba eso\(\angle \mathrm{B}<\angle \mathrm{ACD}\)? QED.

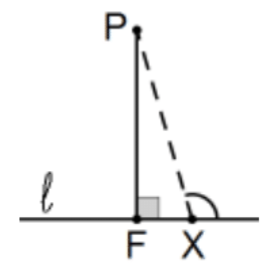
Corolario: La línea de la Prop 12 es única. Es la línea en el punto que es perpendicular a la línea.

Otros corolarios inmediatos son los Apoyos 17 y 27. Algunos otros están a solo un paso de distancia.

Proposición 17. En cualquier triángulo, dos ángulos tomados juntos de cualquier manera son menores que dos ángulos rectos.

Prueba: Nos enfocamos en dos de los ángulos, específicamente los de A y B, de\(\triangle \mathrm{ABC}\). Por ángulos suplementarios,\(\mathrm{m}(\angle \mathrm{CBA})+\mathrm{m}(\angle \mathrm{ABD})=\beta^{\circ}+(180-\beta)^{\circ}\) donde\(\angle \mathrm{ABD}\) es un ángulo exterior no adyacente a\(\angle \mathrm{A}\) así, por la Prop. 16,\(\mathrm{m}(\angle \mathrm{A})<\mathrm{m}(\angle \mathrm{ABD})\) y\(\alpha+\beta<\left(180^{\circ}-\beta\right)+\beta=180^{\circ}\). Por último,\(\alpha+\beta<180^{\circ}\)

Proposición 18. En cualquier triángulo, el lado mayor subtiende el ángulo mayor. [Los ángulos opuestos a los lados mayores son mayores. Nota: Tenga cuidado cuál es cuál.]

Prueba 1: En\(\triangle \mathrm{ABC}\), asuma\(a>b\). \(\alpha>\beta\)Demuéstralo.

Extender rayo\(C A\) a punto\(\mathrm{D}\) tal que\(\mathrm{CD} \cong \mathrm{CB}\). Entonces\(\angle \mathrm{D} \cong \angle \mathrm{CBD}\) (son ángulos base de un triángulo construido para ser isósceles) y el punto\(\mathrm{A}\) está en el interior de\(\angle C B D\) hacer\(\angle C A B\) un ángulo exterior wrt (con respecto a)\(\angle \mathrm{ADB}\) de\(\triangle \mathrm{ADB}\). Por el Teorema del Ángulo Exterior y el hecho de que\(\angle \mathrm{A}=\angle \mathrm{CAB}\), tenemos eso\(\delta<\alpha\), y, ya que el punto\(\mathrm{A}\) es interior a\(\angle \mathrm{CBD}, \mathrm{m}(\angle \mathrm{B})(=\angle \mathrm{CBA})<\mathrm{m}(\angle \mathrm{CBD})\). Por transitividad, tenemos\(m(\angle B)<m(\angle A)\) o\(\alpha>\beta\). QED.

Prueba 2: Como antes, en\(\triangle \mathrm{ABC}\), asumir\(\mathrm{a}>\mathrm{b}\). Esta vez, dejemos\(\mathrm{D}\) estar a lo largo de rayo\(\mathrm{CB}\) tal que\(\mathrm{CD} \cong \mathrm{CA}\) y proceda de manera similar. QED.

Proposición 19. En cualquier triángulo, cuanto mayor ángulo subtiende el lado mayor. [Lo contrario de #18; es decir, los lados opuestos a ángulos mayores son mayores. De nuevo, si..., entonces...?]

Prueba: En\(\triangle \mathrm{ABC}\) la foto como en Prop.18 pero supongamos que\(\angle \mathrm{A}>\angle \mathrm{B}\). Sólo hay tres posibilidades,\(a<b, a=b\), o\(a>b\). En el segundo caso, el triángulo sería isósceles y sus ángulos base congruentes, contradicción con la hipótesis. En el primer caso, aplicando la Proposición 18, tendríamos eso\(\angle \mathrm{A}<\angle \mathrm{B}\); nuevamente, una contradicción. Así\(\mathrm{a}>\mathrm{b}\). QED.

Nota: Aquí, la prueba de la declaración original hizo una prueba de su conversa para ser muy fácil. A menudo ese es el caso (cuando lo contrario es cierto) pero no necesariamente. A veces una prueba de lo contrario de declaración puede ser bastante diferente de usar la validez de la declaración original

Corolario: La distancia más corta de un punto a una línea es la distancia perpendicular.

Prueba: Dejar\(F\) ser el pie de la perpendicular\(P\) y dejar que\(X\) sea cualquier otro punto en la línea. El mayor ángulo en el triángulo resultante es... QED.

Proposición 20 [Desigualdad del triángulo.] En cualquier triángulo, dos lados tomados juntos de cualquier manera son mayores que el restante. Es decir, la distancia más corta entre dos puntos cualesquiera es (sorpresa, sorpresa) la longitud del segmento de línea que los une.

Prueba: En la imagen, lo demostramos\(a+b>c\). Dejar\(D\) ser el punto a lo largo\(\mathrm{BC}\) del rayo de longitud\(\mathrm{b}\) haciendo\(\triangle \mathrm{ACD}\) que sea un triángulo isósceles así que eso\(\angle \mathrm{D} \cong \angle \mathrm{DAC}\). Es claro que\(\angle \mathrm{DAC}<\angle \mathrm{DAB}\) para eso\(\angle \mathrm{ADB}<\angle \mathrm{DAB}\). Por la Prop 19, AB\(<\mathrm{BC}+\mathrm{CD}\). Es decir,\(a+b>c\). QED.

Proposición 21. Si en uno de los lados de un triángulo, desde sus extremidades, se construyen dos líneas rectas que se encuentran dentro del triángulo, las rectas así construidas serán menores que los dos lados restantes del triángulo, pero contendrán un ángulo mayor.

Nota: El lenguaje arcaico es un poco difícil de entender pero la idea es bastante simple. En cualquier triángulo\(\triangle \mathrm{ABC}\), la desigualdad triangular dice que la distancia más corta entre los dos puntos A y C es el segmento de línea que los une. Esta proposición dice que “atravesar” cualquier punto interior D del triángulo es más corto que seguir los lados del triángulo a través de B y que el ángulo determinado es mayor que el ángulo en ese tercer punto B.

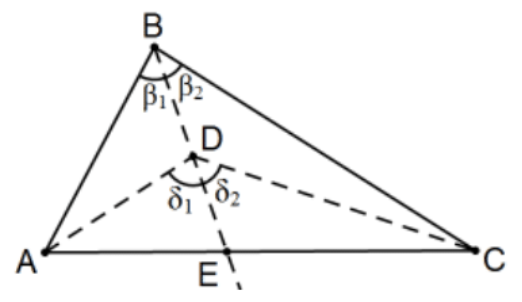
Prueba: La situación del ángulo es la más fácil de las dos. Simplemente considere el rayo\(\mathrm{BD}\) y use el EAT en\(\mathrm{D}\) dividiendo el ángulo\(\mathrm{B}\) en dos ángulos de tamaño\(\beta_{1}\) y\(\beta_{2}\) usando Ray BD que también\(\angle \mathrm{ADC}\) se divide en dos ángulos de tamaño \(\delta_{1}\)y\(\delta_{2}\) con ambos\(\beta_{1}<\delta_{1}\) y\(\beta_{2}<\delta_{2}\) por el teorema del ángulo exterior y sumando,\(\beta=\beta_{1}+\beta_{2}<\delta_{1}+\delta_{2}=\delta\) así\(\angle \mathrm{ABC}<\angle \mathrm{ADC}\). Para la conclusión de la “trayectoria más corta”, extienda el CD de rayos para determinar el punto\(\mathrm{E}\) como se muestra El resultado se desprende del uso cuidadoso del Triángulo Desigualdad:\(\mathrm{AD}<\mathrm{AE}+\mathrm{ED}\) así que\(\mathrm{AD}+\mathrm{DC}<(\mathrm{AE}+\mathrm{ED})+\mathrm{DC}\) y reasociando,\(\mathrm{AD}+\mathrm{DC}<\mathrm{AE}+(\mathrm{ED}+\mathrm{DC})=\mathrm{AE}+\mathrm{EC}\). Pero también\(\mathrm{EC}<\mathrm{EB}+\mathrm{BC}\) para eso\(\mathrm{AE}+\mathrm{EC}<\mathrm{AE}+(\mathrm{EB}+\mathrm{BC})\) y, desde entonces\(\mathrm{AE}+\mathrm{EB}=\mathrm{AB}\), tenemos eso\(\mathrm{AD}+\mathrm{DC}<\mathrm{AB}+\mathrm{BC}\).

Proposición 22. De tres líneas rectas, que son iguales a tres líneas rectas dadas, para construir un triángulo: así es necesario que dos de las líneas rectas tomadas juntas de cualquier manera sean mayores que la restante. [El lenguaje arcaico es incómodo pero la idea es simple.]

Proposición 23. La copia de un ángulo usando la recta y la brújula se realizó inmediatamente después de la Prop\(8.\)

Proposición 24. Si dos triángulos tienen los dos lados iguales a dos lados respectivamente, pero tienen el uno de los ángulos contenidos por las líneas rectas iguales mayor que el otro, también tendrán la base mayor que la base. [El Teorema de la Bisagra, junto con su inversa Prop 25.]

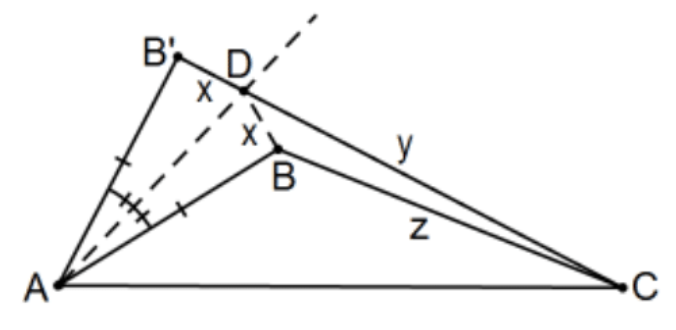
Prueba: En la figura,\(\mathrm{AB} \cong \mathrm{AB}^{\prime}\) y\(\angle \mathrm{BAC}<\angle \mathrm{B}^{\prime} \mathrm{AC}\).

Demostrar\(\mathrm{BC}<\mathrm{B}^{\prime} \mathrm{C}\), o más simplemente,\(\mathrm{x}+\mathrm{y}>\mathrm{z}\).

\(\angle \mathrm{BAB}^{\prime}\)Bisecar para determinar el punto\(\mathrm{D}\) y\(\triangle \mathrm{BAD} \cong \triangle \mathrm{B}^{\prime} \mathrm{AD}\) por\(\mathrm{SAS}\) así\(\mathrm{BD} \cong \mathrm{B}^{\prime} \mathrm{D}\). Pero\(\mathrm{BD}+\mathrm{DC}>\mathrm{BC}\) así terminamos. El panorama podría ser engañoso en que AD podría ser más corto que\(\mathrm{AB}\) pero la prueba es la misma. QED.

Proposición 25. Si dos triángulos tienen los dos lados iguales a dos lados respectivamente, pero tienen la base mayor que la base, también tendrán el uno de los ángulos contenidos por las líneas rectas iguales mayor que el otro. [Lo contrario de la Prop 24 y se desprende fácilmente de ella.]

Proposición 26. Si dos triángulos tienen los dos ángulos iguales a dos ángulos respectivamente, y un lado igual a un lado, es decir, ya sea el lado contiguo a los ángulos iguales, o que subtiende uno de los ángulos iguales, también tendrán los lados restantes iguales a los lados restantes y el ángulo restante al ángulo restante . [Tanto ASA como AAS. Estos son diferentes teoremas con diferentes pruebas por lo que un leve error estructural!]

Comprobante de\(A S A:\) Asumir\(\angle A \cong \angle \mathrm{A}^{\prime}, \angle \mathrm{C} \cong \angle \mathrm{C}^{\prime}\), y\(\mathrm{AC} \cong \mathrm{A}^{\prime} \mathrm{C}^{\prime}\). Dejemos\(\mathrm{B}^{\prime \prime}\) estar a lo largo de rayo\(\mathrm{A}^{\prime} \mathrm{B}^{\prime}\) tal que\(\mathrm{AB} \cong \mathrm{A}^{\prime} \mathrm{B}^{\prime \prime}\). \(\triangle \mathrm{ABC} \cong \triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime \prime} \mathrm{C}^{\prime} \mathrm{by} \mathrm{SAS}\)Entonces así\(\angle C \cong \angle \mathrm{A}^{\prime} \mathrm{C}^{\prime} \mathrm{B}^{\prime \prime}\) por cpctc y, por transitividad,\(\angle \mathrm{C}^{\prime}=\angle \mathrm{A}^{\prime} \mathrm{C}^{\prime} \mathrm{B}^{\prime \prime}\); es decir, uno y el mismo ángulo. Por lo tanto,\(\mathrm{B}^{\prime}=\mathrm{B}^{\prime \prime}\) y ya se sabe que los triángulos deseados son congruentes. QED.

Comprobante de\(A A S: \quad\) Asumir\(\angle \mathrm{A} \cong \angle \mathrm{A}^{\prime}, \angle \mathrm{C} \cong \angle \mathrm{C}^{\prime}\), y\(A B \cong A^{\prime} B^{\prime}\). Dejemos\(C^{\prime \prime}\) estar a lo largo de rayo\(A^{\prime} C^{\prime}\) tal que\(\mathrm{AC} \cong \mathrm{A}^{\prime} \mathrm{C}^{\prime \prime}\). Entonces\(\triangle \mathrm{ABC} \cong \triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{C}^{\prime \prime}\) por\(\mathrm{SAS}\) así\(\angle \mathrm{C} \cong \angle \mathrm{C}^{\prime \prime}\) por cpctc. Si\(\mathrm{C}^{\prime} \neq \mathrm{C}^{\prime \prime}, \Delta \mathrm{B}^{\prime} \mathrm{C}^{\prime \prime} \mathrm{C}^{\prime}\) sería un triángulo no degenerado y por lo tanto violaría el Teorema del Ángulo Exterior. Ya que eso es imposible,\(C^{\prime}=C^{\prime \prime}\) y, como antes, ya se sabe que los triángulos son congruentes. QED.

Proposición 27. Si una línea recta que cae sobre dos líneas rectas hace que los ángulos alternos sean iguales entre sí, las líneas rectas serán paralelas entre sí. [¡Con la Prop 23, existen líneas paralelas!]

Prueba: Supongamos que\(\angle \mathrm{A} \cong \angle \mathrm{B}\) pero las líneas\(\ell\) y se\(m\) cruzan en\(\mathrm{C}\) la imagen. Entonces\(\angle \mathrm{A}\) sería un ángulo exterior no adyacente al ángulo interior\(\angle \mathrm{B}\) con respecto a\(\triangle \mathrm{ABC}\). Pero por\(\mathrm{EAT}, \angle \mathrm{B}<\angle \mathrm{A}\) eso es imposible. Es decir, no hay tal intersección en el lado derecho. Las líneas tampoco pueden cruzarse en el otro lado por la misma razón intercambiando qué ángulo es interior y cuál es exterior. QED.

Proposición 28. Si una línea recta que cae sobre dos líneas rectas hace que el ángulo exterior sea igual al interior y el ángulo opuesto en el mismo lado, o los ángulos interiores del mismo lado iguales a dos ángulos rectos, las líneas rectas serán paralelas entre sí. [Corolarios de la Prop 27.]

Euclides Elements, Book 1, Prop 29 es lo contrario de Prop\(27-8\) y eso significaría que estaríamos en geometría euclidiana ya que (junto con el resto de los axiomas que estamos asumiendo) es lógicamente equivalente al\(5^{\text {th }}\) Postulado de Euclides y muchas variantes algunos de los cuales veremos eventualmente. Por ahora, nos estamos enfocando en la geometría neutra o, por otro nombre común, absoluta. Aunque hay muchos teoremas posteriores en los Elementos de Euclides (incluso en los libros que suceden al Libro 1) que son teoremas de geometría neutra con pruebas idénticas, el hecho de que Euclides llegó tan lejos sin usar el\(5^{\text {th }}\) Postulado, incluyendo la forma limitada del Teorema del Ángulo Exterior, es indicación persuasiva de que los griegos estaban haciendo todo lo posible para probarlo como teorema en lugar de aceptarlo a regañadientes como otro axioma. Durante muchos siglos a partir de entonces, muy buenos geómetros realizaron un extenso trabajo en intentos fallidos de probarlo. Tocaremos un poco de eso en los esfuerzos preliminares de Saccheri y Lambert en el próximo capítulo. Solo la eventual aceptación de todos los demás axiomas junto con la negación del\(5^{\text {th }}\) Postulado de Euclides como geometría legítima por derecho propio, la geometría hiperbólica, resolvió el problema milenario ahora conocido como geometría moderna.