1.3: Conjunto de problemas 1

Última actualización
Guardar como PDF

Page ID: 118038

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Los Exs 1-6 se refieren al triángulo isósceles representado con ángulos de base en B y C. En cada uno, indican en un boceto correspondiente toda la información dada de manera estándar y, igualmente importante, nada más que la información dada. Luego demuestre que los ángulos de base son congruentes libremente usando, según corresponda, cualquiera de las declaraciones de congruencia estándar SAS, SSS, ASA, AAS e Hipotenuse-Leg.

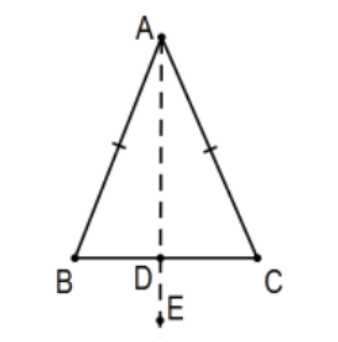
$Screen Shot 2022-06-23 a las 12.09.35 PM.png$

Supongamos que ese punto$\mathrm{D}$ es el punto determinado por el rayo$\mathrm{AE}$, la bisectriz de$\angle \mathrm{A}$.
Supongamos que el punto$\mathrm{D}$ es el punto medio del segmento de línea BC.
Supongamos que el punto$\mathrm{D}$ está determinado por la perpendicular desde (on) punto A a la línea BC.
Explique por qué la imagen es engañosa si asumiera que la línea$\mathrm{DE}$ es la bisectriz perpendicular del segmento BC para que su prueba resultante probablemente sea defectuosa (es decir, no es una prueba en absoluto).
Usando solo isósceles$\triangle \mathrm{ABC}$ (es decir, sin puntos o líneas auxiliares) y SAS.
Usando solo isósceles$\triangle \mathrm{ABC}$ (es decir, sin puntos o líneas auxiliares) y SSS.
Proposición 9 en Elementos de Euclides, Libro 1, y se traduce como, “Biseccionar un ángulo rectilíneo dado”. Construir la bisectriz de un ángulo y demostrar que es válido.
Construya una línea perpendicular a una línea desde (o “on”) un punto que no esté en la línea y demuestre que su construcción es válida.
Construye una línea perpendicular a una línea en un punto que está en la línea y prueba tu construcción. [Nota: Tanto en los Exs 8 como en el 9, el artículo indefinido “a” es deliberado pero, y como se remarca en el texto por distintas razones, ambas líneas son únicas por lo que “la”.]
Las definiciones son cruciales para las matemáticas aunque generalmente no voy a pedirle que cite ninguna de las estándar de geometría euclidiana elemental. Para cada uno, exponer la esencia de su definición; es decir, sólo la información conocida sobre la figura geométrica o situación por definición. Incluir un boceto de un representante de cada situación e indicar en él sólo la información dada de su definición.

i. triángulo isósceles xii. ángulos complementarios xxiii. rombo

ii. ángulo recto xiii. ángulos suplementarios xxiv. bisectriz

iii. rectángulo$\quad$ xiv. línea tangente$\quad x x v$. polígono regular

iv. triángulo escaleno$\quad \mathrm{xv}$. círculos concéntricos$\quad$ xxvi. mediana

v. triángulo obtuso xvi. trapecio$\quad$ xxvii. altitud

vi. triángulo rectángulo$\quad$ xvii. trapecio isósceles$\quad$ xxviii. líneas concurrentes

vii. cuadrado xviii. radio$\quad$ xxix. líneas oblicuas

viii. líneas paralelas$\quad$ xix. diámetro$\quad$ xxx. paralelogramo

ix. ángulos verticales$\quad$ xx. círculos tangentes$\quad$ xxxi. ¡Agrega el tuyo propio!

x. líneas perpendiculares$\quad$ xxi. dentro del círculo de un polígono (no es necesario existir)

xi. polígono xxii. circuncírculo de polígono (no necesita existir)

11. Estado (en inglés moderno, coherente, matemático) y probar la Proposición 6 de los Elementos de Euclides, lo contrario de los ángulos de base de un teorema de triángulo isósceles.

12. Estado (en inglés moderno, coherente, matemático) y probar la Prop. 18 de Euclides Elements', “En cualquier triángulo el lado mayor subtiende el ángulo mayor”. Completar la segunda prueba indicada.

Estado (en inglés matemático moderno y coherente) y probar la Prop. 19 de Euclides Elements', lo contrario del resultado en el Ex$12 .$
Considera la afirmación: Todos los cuadrados son rectángulos.

a.- Por la definición inclusiva (la habitual en matemáticas), la afirmación es verdadera. Declararlo como implicación; es decir, cambiar el enunciado a “Si p, entonces$q$" forma.

b. Declarar su contrario como implicación formal y reafirmar la implicación en forma casual (de uso común).

c. ¿Es cierto? Demuestra tu aseveración.

15. Demostrar que la distancia más corta de un punto a una línea es a lo largo de la perpendicular.

Una línea se define para ser tangente a un círculo si se cruzan exactamente en 1 punto. Demostrar que una línea que cruza un círculo es tangente al círculo si y sólo si es perpendicular al radio que determina.
Una vez más, Ex 9 dice "$a$perpendicular de un punto a una línea”, no "la perpendicular de un punto a una línea. Demostrar que el artículo definido es correcto y argumentar que en una esfera tal línea no necesita ser única. [Pista: El Polo Norte y el Ecuador pueden ser útiles aquí.] Es "el" bajo los axiomas de geometría neutra pero esto es algo sutil, consecuencia del Teorema del Ángulo Exterior, Prop.16.]
Construir la copia de un triángulo y demostrar que la construcción es válida. [Nota: Esto no es “duplicar ese triángulo”; eso es un uso arcaico que significa duplicar su área.]
Una cometa es un cuadrilátero con dos pares de lados adyacentes congruentes (la forma de una cometa tradicional).

i. Demostrar que las diagonales de una cometa son perpendiculares.

ii. Indicar una forma razonable (es decir, suave, sondeo no artificial) de lo contrario de$19 i$.

iii. Demostrar o desacreditar$19 i i$.

Teorema: Un punto está en la bisectriz perpendicular de un segmento de línea si y solo si es equidistante de cada uno de sus puntos finales. Nota: Una forma alternativa para este teorema, especialmente en libros más antiguos es, “El locus de todos los puntos equidistantes de dos puntos es la bisectriz perpendicular del segmento de línea que los une”.
Dados tres puntos en un círculo, construir el centro del círculo.

Nota 1: Este lenguaje significa más de lo que dice; significa explicar un procedimiento de construcción y demostrar que su trámite es válido.

Nota 2: No construya bisectores perpendiculares de los 3 acordes determinados. ¿Por qué no?

Parte de la Proposición 26 (tanto ASA como AAS) es mejor pensada como “Si SAS, entonces ASA”. Declarar su contrario y probarlo. [Sugerencia: Ver los comentarios sobre SSS al final de la Introducción.]
Un cuadrilátero con la propiedad de que sus cuatro ángulos hacen dos pares de ángulos congruentes sucesivos (comparten un lado) es un trapecio isósceles. Corolario: Los lados opuestos de un rectángulo son congruentes. [Sugerencia: Considere la bisectriz perpendicular de cualquiera de las bases e incluya diagonales para hacer triángulos congruentes.]