2.1: Geometría elemental neutra
- Page ID
- 118067
La mayoría de los siguientes resultados datan de la antigüedad pero, aunque sea así, usaremos consistentemente el lenguaje moderno y tú también deberías hacerlo. Además, trata de tener cuidado con el simbolismo. Es muy difícil para mí hacer eso en mi procesador de textos pero siempre agregar símbolos distintivos según corresponda - ¡Haz lo que digo, no como yo hago! Por ejemplo, el segmento de línea\(\overline{A B}\) debe escribirse con una barra sobre él, rayo\(\overline{A B}\) con una flecha, el mismo rayo podría indicarse escribiendo BA con la flecha invertida (que mi procesador de textos no puede hacer), y línea\(\overrightarrow{\mathrm{AB}}\) con una flecha de dos puntas. Tenga en cuenta que el segmento de línea\(\overline{\mathrm{AB}}\) es igual al segmento de línea\(\overline{\mathrm{BA}}\) como conjuntos. Es decir, son uno y el mismo conjunto pero rayos\(\overrightarrow{\mathrm{AB}}\) y no\(\overrightarrow{\mathrm{BA}}\) son el mismo conjunto. Formalmente:
segmento\(\overline{\mathrm{AB}}=\{\mathrm{X} \mid \mathrm{X} \in \overrightarrow{\mathrm{AB}}\) con\(\mathrm{X}=\mathrm{A}, \mathrm{X}=\mathrm{B}\), o\(\mathrm{X}\) entre\(\mathrm{A}\) y\(\mathrm{B}\}\), y rayo\(\mathrm{AB}=\{\mathrm{X} \mid \mathrm{X} \in \overrightarrow{\mathrm{AB}}\) con\(\mathrm{X}=\mathrm{A}, \mathrm{X}=\mathrm{B}, \mathrm{X}\) entre\(\mathrm{A}\) y\(\mathrm{B}\), o\(\mathrm{B}\) entre\(\mathrm{A}\) y\(\mathrm{X}\}\).
¿Tiene sentido “entre”? ¡Tenía mejor! Este es otro ejemplo más de nuestra semiformalidad.
El uso de estas convenciones consistentemente “libera” el uso de AB sin modificadores simbólicos para indicar la medida del segmento de línea\(\overline{\mathrm{AB}}\); es decir, la distancia de\(\mathrm{A}\) a\(\mathrm{B}, \mathrm{m}(\overline{\mathrm{AB}})\), se puede simplificar como\(\mathrm{AB}\).
Si bien la congruencia es un término indefinido en una geometría estrictamente formal, nuestros axiomas siempre tienen un concepto de longitud de un segmento lineal (el Postulado Gobernante) y medida de ángulo (el Postulado Transportador) y, con esos, la idea que queremos puede ser (¡y es!) definida como una correspondencia uno a uno que preserva la distancia entre dos puntos cualesquiera y la medida de dos ángulos correspondientes cualesquiera. [Nota: “Conservar distancia” hace que el “uno a uno” sea redundante.] Cualquier conjunto es congruente consigo mismo en abstracto pero decir\(\overline{\mathrm{AB}} \cong \overline{\mathrm{BA}}\) es afirmar más que su igualdad establecida; implica tal correspondencia conservadora de distancia pero en orden inverso. Es decir,\(A\) se “mapea hacia”\(B\), el punto\(1 / 3\) del camino desde\(A\)\(B\) hasta el punto\(1 / 3\) del camino desde\(B\) hasta A, etc.; es decir, todos los demás puntos igualmente. Es cierto aunque no nos preocuparemos por tales cosas a menos que nos regañen pero, por el bien de la integridad, es el reflejo del segmento en su bisectriz perpendicular. De igual manera,\(\angle \mathrm{ABC} \cong \angle \mathrm{CBA}\) es cierto pero no sólo porque son uno y el mismo conjunto; es decir, no por la “propiedad reflexiva de la congruencia” (¡aunque lo verás en muchos libros de geometría elemental!). Nuevamente hay una congruencia subyacente, es decir, la reflexión del ángulo en la línea que biseca el ángulo.
De hecho, es incluso más profundo que una distancia y un ángulo preservando la correspondencia entre los dos conjuntos. Para ser formal al respecto, una congruencia se define como una correspondencia uno a uno, preservando la distancia, preservando el ángulo desde todo el conjunto de puntos de la geometría sobre sí mismo. Es decir, la aseveración de que dos figuras son congruentes es una aseveración de que todo el conjunto de puntos se puede emparejar consigo mismo de una manera que conserve todas las distancias y ángulos ya que “lleva” una figura sobre la otra. En la geometría del plano euclidiano, una traslación (planeo o diapositiva, en algunos libros elementales), una rotación alrededor de un punto fijo y una reflexión a través de una línea fija son todas congruencias, así como composiciones de las mismas. ¿Hay otros? ¿Estas congruencias son también de la denominada geometría “neutra”? Las respuestas son no, sí, y sí pero no nos preocuparemos por ello hasta el Capítulo 5 aunque algunas presentaciones se construyen en torno a él. Todavía no hemos probado el último de los teoremas de congruencia:
Dos triángulos rectos con hipotenusas congruentes y un par de piernas congruentes son congruentes. Reexpresado específicamente:
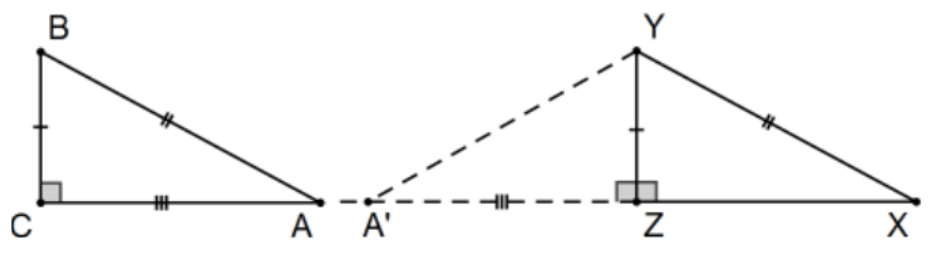
Dado:\(\triangle \mathrm{ABC}\) y\(\triangle \mathrm{XYZ}\) con\(\angle \mathrm{C}\) y ángulos\(\angle \mathrm{Z}\) rectos,\(\mathrm{AB} \cong \mathrm{XY}\), y\(\mathrm{BC} \cong \mathrm{YZ}\)
Demostrar:\(\triangle \mathrm{ABC} \cong \triangle \mathrm{XYZ}\)
Prueba: Llevar\(\mathrm{A}^{\prime}\) a lo largo de rayo\(\mathrm{XZ}\) con\(\mathrm{ZA}^{\prime} \cong \mathrm{CA}\). Entonces\(\triangle \mathrm{A}^{\prime} \mathrm{YZ} \cong \triangle \mathrm{ABC}\) por SAS así\(\mathrm{A}^{\prime} \mathrm{Y} \cong \mathrm{AB}\) y, por transitividad,\(\mathrm{A}^{\prime} \mathrm{Y} \cong \mathrm{XY}\) así\(\triangle \mathrm{A}^{\prime} \mathrm{YX}\) es isósceles. Entonces\(\angle \mathrm{A}^{\prime} \cong \angle \mathrm{X}\) pero\(\angle \mathrm{A}^{\prime} \cong \angle \mathrm{A}\) por cpctc así\(\triangle \mathrm{A}^{\prime} \mathrm{YZ} \cong \triangle \mathrm{XYZ}\) por\(\mathrm{AAS}\) (en un par de maneras diferentes). Finalmente,\(\triangle \mathrm{ABC} \cong \triangle \mathrm{XYZ}\) por transitividad. QED.
Seleccione tres puntos cualesquiera en el círculo dado y construya los bisectores perpendiculares de cualquiera de los tres acordes que determinan. Estos sí se cruzan y su punto de intersección es el centro del círculo.
Prueba: (PS 1, #21) Conócelo, su prueba, y muchas otras fáciles.
Nota 1: ¿Por qué no los tres pares? Pista: No está mal pero hace que la prueba sea mucho más difícil. ¿Por qué?
Nota 2: Esto no prueba que ningún triángulo tenga un circuncírculo porque no prueba que los bisectores perpendiculares de dos de sus lados se crucen. Si se cruzan, entonces los 3 vértices del triángulo son equidistantes de ese punto de intersección y el conjunto de todos los puntos equidistantes de ese punto es un círculo que contiene los 3 vértices, de ahí el circumcircle, y el punto de intersección es su centro, llamado circuncentro del triángulo. Obsérvese que este punto es equidistante de cada par de puntos en el círculo y por lo tanto en su bisectriz perpendicular por lo que todos esos bisectores perpendiculares son concurrentes. En nuestro caso, los tres puntos ya estaban en círculo por lo que, obviamente, su centro debe estar sobre cada uno de los dos bisectores perpendiculares. Por lo tanto, deben cruzarse para identificar el centro. QED.
Teorema: Tangente iff Perpendicular al Radio: Una línea que cruza un círculo en un punto es tangente al círculo en ese punto si es perpendicular al radio a ese punto de intersección.
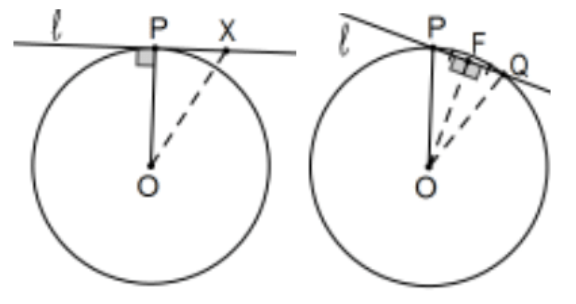
Prueba: Primero el “si”, supongamos que\(\mathrm{P}\) está en círculo\(\mathrm{O}\) y la línea dada\(\ell\) es perpendicular al radio OP. Dejar\(X\) ser cualquier punto en la línea que no sea\(\mathrm{P}\). Entonces\(\triangle \mathrm{OPX}\) es un triángulo rectángulo con hipotenusa\(\mathrm{OX}>\mathrm{OP}\) que obliga\(X\) a estar fuera del círculo por lo que solo un punto de intersección de línea\(\ell\) y círculo\(\mathrm{O}\). Por definición de tangente, la línea es tangente al círculo en ese punto. Por el contrario, supongamos que la línea\(\ell\) es tangente al círculo O y deja\(\mathrm{F}\) ser el pie de la perpendicular de\(\mathrm{O}\) a la línea. Si fuera cierto eso\(\mathrm{F} \neq \mathrm{P}\), que\(\mathrm{Q}\) sea el punto en el lado opuesto de\(F\) con el\(F Q \cong F P\). Entonces\(\triangle O F Q \cong \triangle O F P\), por\(S A S\), así\(O Q \cong O P\) y\(Q\) sería un segundo punto de línea\(\ell\) sobre círculo\(\mathrm{O}\) y la línea no es tangente desde entonces\(\mathrm{Q} \neq \mathrm{P}\). Esto prueba lo inverso (si no perpendicular, entonces no tangente), no lo contrario como se esperaba, sino que son lógicamente equivalentes. QED.
Teorema: Para Construir el Círculo de un Triángulo:
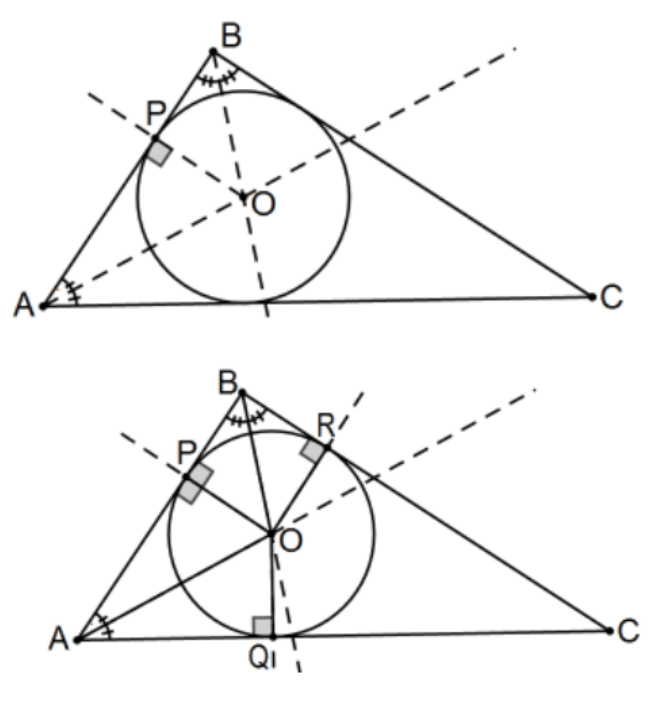
Construcción: Construir los bisectores de dos de los ángulos del triángulo. El no especificado (!) los axiomas sí garantizan que se crucen (ya que están dentro del triángulo cerrado y acotado). Ese punto es el incentro del triángulo. Para determinar el radio, construya la perpendicular a cualquiera de sus lados. Con el centro y el radio construidos, se construye el círculo.
Prueba: Dejar\(\mathrm{Q}\) y\(\mathrm{R}\) ser las perpendiculares a los otros dos lados donde\(\mathrm{O}\) se determinó por los bisectores de ángulos\(\mathrm{A}\) y\(\mathrm{B}\). \(\triangle \mathrm{AOP} \cong \triangle \mathrm{AOQ}\)y\(\triangle \mathrm{BOP} \cong \triangle \mathrm{BOR}\) por AAS para que\(\mathrm{OP} \cong \mathrm{OQ} \cong \mathrm{OR}\). Eso implica eso\(\mathrm{P}, \mathrm{Q}\), y\(\mathrm{R}\) se encuentran en el círculo con centro en\(\mathrm{O}\) y radio OP. La perpendicularidad de los radios con cada uno de los lados implica que este círculo es tangente a cada uno de los lados, el incircle.
Corolario: Los bisectores angulares de un triángulo son concurrentes.
Prueba: Simplemente demuestre que el rayo (ya determinado) desde el tercer vértice\(\mathrm{C}\) a través del incenter\(\mathrm{O}\) en la prueba del teorema anterior biseca ese tercer ángulo. [Pista: Usar Hipotenusa-Pierna.] QED.
Nota: Este enfoque para demostrar que las entidades que comparten alguna descripción común comparten alguna otra descripción común es importante: Dejar de “construir” tan pronto como se determine la entidad necesaria y pruebe todo lo demás al respecto. Si no, la prueba se hace mucho más difícil al tener que demostrar que aparentemente diferentes entidades son realmente una y la misma. Es decir, O se determinó biseccionando dos de los ángulos. Bisecar el tercer ángulo determinaría (ostensiblemente) dos puntos más que tendrían que mostrarse para ser el mismo punto. Evita el problema nunca “sobredeterminando” nada. Deja de decir “let x be” cuando\(x\) se determine y demuestre todo lo apropiado al respecto. Como otro ejemplo de la construcción, la segunda y tercera perpendiculares no formaban parte de la construcción real, sólo parte de la prueba de validez.
Teorema: Teorema de la suma de ángulos (forma de geometría neutra): La suma de los ángulos de un triángulo no es mayor que dos ángulos rectos. [Así que para un\(n\) -gon, no mayor que\(180(n-2)\).]
Prueba: Una buena prueba es una extensión de la prueba previa del Teorema del Ángulo Exterior pero primero consideramos algunas ideas preliminares.
[Nota: Ya no estamos en nuestro “mundo real” literal; es decir, la vida en una esfera. Aquí no hay líneas paralelas (dos líneas cualesquiera se cruzan en puntos antípodas; es decir, el punto medio del segmento euclidiano que determinan es el centro de la esfera). Considera un triángulo determinado por dos segmentos de línea longitudinal desde el Polo Norte hasta el Ecuador y el segmento del Ecuador que determinan. La suma del ángulo de dicho triángulo es\(90^{\circ}+\)\(90^{\circ}+x^{\circ}\) donde\(x^{\circ}\) está la medida del ángulo en el Polo Norte. ¿Qué hay de malo en la prueba; algo debe ser?! Pista: El tamaño importa en una esfera. ¿Qué es “demasiado grande”? Ver PS 2, #27.]
Definición: Dos polígonos son equivalentes si uno puede ser cortado en un número finito de polígonos y las piezas reordenadas para hacer el otro; es decir, para encajar perfectamente. [Una definición formal de esto es complicada, ¡así que no nos molestaremos!] Ejemplo: Recorta un\(2 \times 8\) rectángulo en el centro y reordena para obtener un\(4 \times 4\) cuadrado.
¿Pregunta? ¿Qué es un rectángulo? ¿Hay alguna? Respuesta: Sí (en geometría euclidiana) o No (hiperbólico).
Nota: El área no ha sido definida pero, sea lo que sea, ¡debería ser lo mismo para cifras equivalentes!
Teorema: Si dos triángulos son equivalentes, entonces tienen la misma suma de ángulos. De manera más general, si un triángulo es equivalente a un\(n\) -gon la diferencia de sus sumas de ángulo es\(180(n-3)\).
Prueba: Agitar a mano. No se supone que hagamos eso en matemáticas pero una prueba formal se pondría en el camino y no sería útil. La idea es que los vértices introducidos por el corte estarán en el interior donde se suman los ángulos constituyentes\(360^{\circ}\) o a lo largo de un borde al que se suman\(180^{\circ}\). Como estas piezas se reordenan, el ajuste perfecto requiere la misma situación. Una prueba formal sería por algún tipo de inducción matemática complicada. Afortunadamente, no necesitamos toda la potencia de este resultado para completar la prueba del Teorema de la Suma de Ángulo; podemos probar lo que necesitamos a medida que avanzamos:
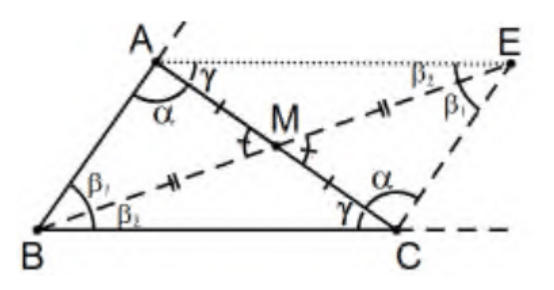
En la prueba del Teorema del Ángulo Exterior, Prop 16, es fácil ver que\(\triangle \mathrm{EBC}\) es equivalente al original\(\triangle \mathrm{ABC}\). En el proceso,\(\angle \mathrm{B}\) se dividió en dos ángulos y que cada subángulo está involucrado en este nuevo triángulo,\(\angle \mathrm{EBC}\) es uno de esos ángulos y\(\angle \mathrm{EBA} \cong \angle \mathrm{BEC}\) es el otro. Además,\(\angle \mathrm{A}\) es congruente a\(\angle \mathrm{ECM}\) eso es una parte componente de\(\angle B C E\) con el original\(\angle C\) siendo el resto de\(\angle B C E\). Por lo tanto, la suma angular de esta nueva\(\triangle E B C\) es la misma que la original\(\triangle \mathrm{ABC}\). Si, como es habitual, tomamos\(\mathrm{m}(\angle \mathrm{B})=\beta\) y tomamos las medidas de los dos ángulos subdivididos\(\beta=\beta_{1}+\beta_{2}\) como se indica, al menos uno de\(\beta_{1}\) o\(\beta_{2}\) debe ser menor o igual a\(\beta / 2\) porque, si ambos fueran mayores que \(\beta / 2\), su suma superaría\(\beta\), una imposibilidad. En nuestra figura, el más pequeño parece ser\(\beta_{2}\), en cuyo caso, procederíamos con\(\Delta\) EBC como se muestra en la foto pero iba a ser\(\beta_{1}\), usaríamos\(\triangle \mathrm{EBA}\), también en la foto y también equivalente a\(\Delta \mathrm{ABC}\) y donde todos se aplican las mismas observaciones.
Finalmente, estamos listos para comenzar una prueba indirecta; es decir, asumir que esta\(\triangle \mathrm{ABC}\) es una con suma de ángulo mayor que\(180^{\circ}\). Expresar este “exceso” por\(\varepsilon>0\). En otras palabras,\(\alpha+\beta+\gamma=180+\varepsilon\). El nuevo triángulo,\(\Delta \mathrm{EBC}\) tiene la misma suma angular pero con el nuevo ángulo a\(B\) de medida menor o igual a\(\beta / 2^{=} \beta / 2^{1}\).
Repitiendo la misma construcción (es decir, con la mediana de B hasta el punto medio del lado CE, obtenemos un triángulo con la misma suma de ángulos pero, esta vez, la medida del ángulo a\(B\) es menor o igual a\(\beta / 2^{2}\), y repitiendo\(n\) tiempos, \(\beta / 2^{n}\)donde, por suficientemente grande\(n, \beta / 2^{n}<\varepsilon\). Entonces, ¿qué? Por la Prop 17, los otros dos ángulos tienen una suma, digamos x, de menos que\(180^{\circ}\) así sumando en el ángulo en B, digamos y, tenemos un triángulo con suma de ángulo de\(180+\varepsilon=x+y\) con\(x<180\) y\(y<\varepsilon\). Obviamente, esto no puede ser así; no existe tal triángulo y la suma angular de cualquier triángulo no supera\(180^{\circ}\). QED.
Corolario: Si una línea cruza dos lados de un rectángulo la divide en dos polígonos sin “déficit”; es decir, sus sumas angulares menores no pueden ser de lo que “deberían ser”. Por ejemplo, si uno de los polígonos es un triángulo rectángulo, entonces los otros dos ángulos son complementarios o, si se trata de un cuadrilátero, los dos ángulos adyacentes que no se sabe que son ángulos rectos son complementarios. La idea es que si cualquiera\(n\) -gon resultante tiene suma de ángulo estrictamente menor que\(180^{\circ}(\mathrm{n}-2)\), entonces... [Pero, de nuevo, ¿hay rectángulos? Espere hasta el siguiente capítulo.]
Corolario: Los lados opuestos de un rectángulo son congruentes. [Nota: Esto fue un corolario de PS 1, #23.] Además, no es un teorema sobre los paralelogramos en general.]
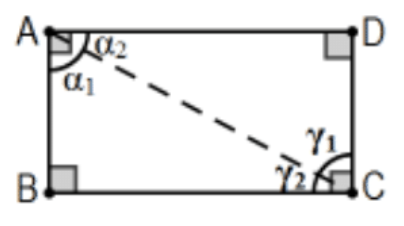
Prueba: Cualquiera de las diagonales de un rectángulo lo divide en dos triángulos rectos. No puede haber “déficit”, la suma angular de cada uno debe ser\(180^{\circ}\), ya que los dos ángulos agudos de cada uno componen un ángulo recto del rectángulo. Específicamente con referencia al rectángulo representado, cada ángulo de vértice es un ángulo recto de manera que\(\alpha_{1}+\alpha_{2}=\gamma_{1}+\gamma_{2}=90^{\circ}\) y, ya que cada triángulo tiene una suma de ángulo menor o igual\(180^{\circ}, \alpha_{1}+\gamma_{2} \leq 90^{\circ}\) y\(\alpha_{2}+\gamma_{1} \leq 90^{\circ}\). Si alguna de estas desigualdades fuera estricta (es decir\(\left.<\right)\),, tendríamos\(\left(\alpha_{1}+\gamma_{2}\right)+\left(\alpha_{2}+\gamma_{1}\right)<180^{\circ}\) y, reordenando los términos,\(180^{\circ}=\left(\alpha_{1}+\alpha_{2}\right)+\left(\gamma_{1}+\gamma_{2}\right)<180^{\circ}\). Esta contradicción obliga a ambos\(\alpha_{1}+\gamma_{2}=90^{\circ}\) y\(\alpha_{2}+\gamma_{1}=90^{\circ}\). Es decir,\(\alpha_{1}=90^{\circ}-\gamma_{2}=\gamma_{1}\) y\(\alpha_{2}=90^{\circ}-\gamma_{1}=\gamma_{2}\). Cualquiera de las ecuaciones solas, junto con los ángulos rectos en\(\mathrm{B}\)\(\mathrm{D}\) y y la diagonal común, implica eso\(\triangle \mathrm{ACD} \cong \triangle \mathrm{CAB}\) por AAS o, usándolos ambos, por ASA. En cualquier caso, por cpctc, los lados opuestos son congruentes.
Teorema: ASA para Triángulos Largos. En primer lugar, no existe tal cosa; es decir, un "triángulo largo" no es un triángulo en absoluto. Es un nombre conveniente para una figura que es la unión de dos rayos que, junto con el segmento de sus puntos iniciales, no se cruzan. [Nota: Este nombre no se usa universalmente en geometría.]
[Nota: Esta era una definición; ¡necesitas conocer definiciones aunque nunca se hayan escrito!] ¿El teorema? Efectivamente, si ABCD y EFGH son figuras geométricas tales que\(\angle B \cong \angle F, \angle C \cong \angle G\), y segmentos\(B C \cong F G\), entonces los rayos BA y CD se cruzan si los rayos FE y GH se cruzan. [Equivalentemente, un par no se cruza si el otro par no se cruza; es decir, uno es “largo” si el otro lo es.]
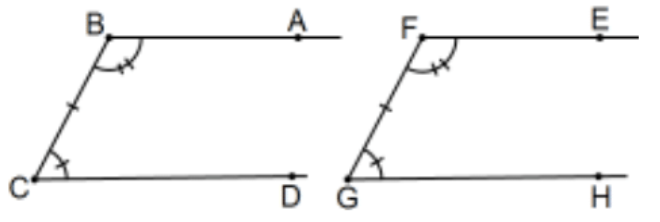
Prueba: Supongamos que los rayos BA y CD sí se cruzan, dicen en\(\mathrm{X}\), y toman\(\mathrm{Y}\) junto\(\mathrm{GH}\) con\(\mathrm{GY} \cong \mathrm{CX}\). Después\(\triangle \mathrm{BCX} \cong \triangle \mathrm{FGY}\) por SAS y\(\angle C B X \cong \angle G F Y\) por cpctc. Pero\(\angle C B X=\angle C B A=\angle B\) (es decir, uno y el mismo ángulo) así, por hipótesis y el Postulado Transtractor, también\(\mathrm{Y}\) está sobre el rayo FE, el punto de intersección con el rayo GH. QED.
Nota: Estos triángulos largos son “congruentes”; es decir, existe una correspondencia uno a uno tal que se conservan todas las distancias y ángulos) y esta prueba podría limpiarse para acomodarla. No lo vamos a necesitar.
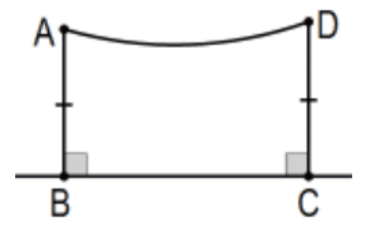
Definición: Un cuadrilátero Saccheri es un cuadrilátero con un par de lados opuestos, llamados patas, que son congruentes y perpendiculares a (en el mismo lado de) la línea de su base. Su cuarta cara se llama su cumbre. Por ejemplo, la Fig. ABCD es un cuadrilátero Saccheri ya que las líneas\(\mathrm{AB}\) y\(\mathrm{CD}\) son perpendiculares a línea\(\mathrm{BC}\) y segmentos\(\mathrm{AB} \cong \mathrm{DC}\). En este caso, estos segmentos son las patas, el segmento\(\mathrm{BC}\) es la base y el segmento AD es la cumbre. La línea AD es la línea cumbre.
Teorema: Los ángulos de cumbre de un cuadrilátero Saccheri son congruentes (y por lo tanto no obtusos).
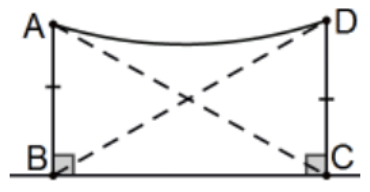
Prueba 1: Conocer varios y poder terminar correctamente cualquier aviso que pudiera dar. Probablemente la prueba más obvia utiliza las diagonales AC y\(\mathrm{BD}\) como se indica. Obviamente,\(\triangle \mathrm{ABC} \cong \triangle \mathrm{DCB}\) por SAS para que\(\mathrm{AC} \cong \mathrm{DB}\) y\(\triangle \mathrm{ABD} \cong \triangle \mathrm{DCA}\) por SSS para que el original\(\angle \mathrm{A} \cong \angle \mathrm{D}\) por cpctc. QED.
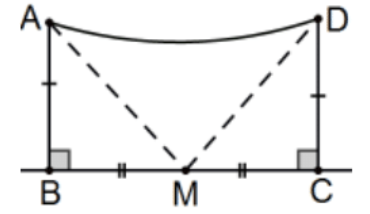
Prueba 2: Una prueba menos obvia pero aún fácil es usar exactamente un punto auxiliar, el punto medio\(\mathrm{M}\) de la base\(\mathrm{BC}\) como se muestra en la imagen. Obviamente,\(\triangle \mathrm{ABM} \cong \triangle \mathrm{DCM}\) por SAS de manera que\(\mathrm{AM} \cong \mathrm{DM}\) y\(\triangle \mathrm{AMD}\) es isósceles por lo que sus ángulos de base son congruentes por teorema anterior. Combinado con el otro par de ángulos congruentes en A y D (por cpctc), tenemos otra prueba de que los ángulos de cumbre son congruentes. \(\quad\)QED.
Nota 1: Como cuestión de buena forma en una situación como en esa segunda prueba, diga algo así como, “Let\(\mathrm{M}\) be the midpoint of line segment BC.” pero no digas nada sobre “dejar” o “construir” nada más. En ese punto, el segmento AM, rayo AM, y otros similares que puedan ser necesarios ya existen. Solo úsalos.
Nota 2: Un cuadrilátero Saccheri no necesita (al menos aún no probado) ser un rectángulo. En geometría euclidiana, resultan ser uno y lo mismo pero en geometría neutra, los ángulos de cumbre pueden ser o no ángulos rectos. ¿Qué es un rectángulo? [Pista: Aclara tu garganta mientras dices “correcto” como si fueras Olde Englisch.]
Teorema: En un cuadrilátero Saccheri, estas son la misma línea:
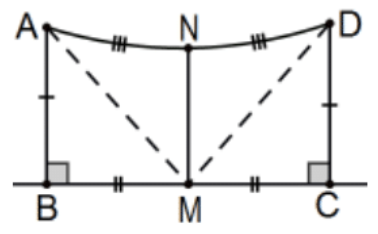
i. La línea de los puntos medios de la base y la cumbre.
ii. La bisectriz perpendicular de la base.
iii. La bisectriz perpendicular de la cumbre.
Prueba: Ver PS 2, #12 -16. Para i implica ii y iii:
Dejar\(M\) ser el punto medio de la base y\(N\) el punto medio de la cumbre del cuadrilátero Saccheri ABCD como se muestra en la foto. Entonces\(\triangle \mathrm{ABM} \cong \triangle \mathrm{DCM}\) por SAS así\(\mathrm{AM} \cong \mathrm{DM}\) por cpctc y\(\triangle \mathrm{AMN} \cong \triangle \mathrm{DMN}\) por SSS. Finalmente, los ángulos en\(\mathrm{N}\) son ambos congruentes (cpctc) y suplementarios por lo tanto la línea MN es perpendicular a la cumbre y, al sumar pares de ángulos congruentes, también es perpendicular a la base. Ya que se dio que biseccionó cada uno (es decir, “let”), la línea es la bisectriz perpendicular de cada uno. QED
Nota: Las (líneas de) la base y cumbre de un cuadrilátero saccheri comparten una perpendicular común. Por lo tanto, entre otras cosas, son paralelos por el EAT. Otro resultado de esta prueba es que aporta más pruebas del teorema anterior; los ángulos de cumbre de un cuadrilátero saccheri son congruentes.
Teorema: [Cuadrilátero Saccheri Asociado] En un triángulo, considere la línea determinada por los puntos medios de dos lados y las perpendiculares a esa línea desde los dos vértices del mismo lado de esa línea. Los segmentos determinados forman un cuadrilátero Saccheri que es equivalente al triángulo original con ángulos de cumbre tales que su suma es la suma de los ángulos interiores del triángulo.
[¿Cuáles son su base, patas y cumbre?]
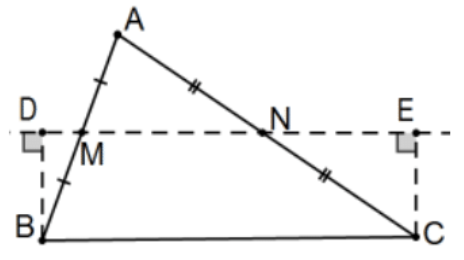
Construcción: Conócelo. En\(\triangle \mathrm{ABC}\), dejar\(\mathrm{M}\) y\(\mathrm{N}\) ser los puntos medios de dos de sus lados; en el caso representado, los segmentos AB y AC, respectivamente. Dejar\(\mathrm{D}\) y\(\mathrm{E}\) ser los pies de las líneas perpendiculares a la línea\(\mathrm{MN}\) desde los dos vértices de\(\triangle \mathrm{ABC}\) en un mismo lado de línea\(\mathrm{MN}\); en este caso, vértices\(B\) y C. Entonces BDEC es el deseado Saccheri cuadrilátero con cumbre BC.
Nota: Esta es la construcción de sólo uno de los tres cuadriláteros asociados de\(\triangle \mathrm{ABC}\); hay otro con cumbre\(\mathrm{AB}\) y un tercero con cumbre AC.
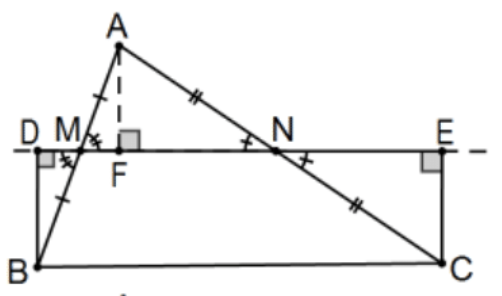
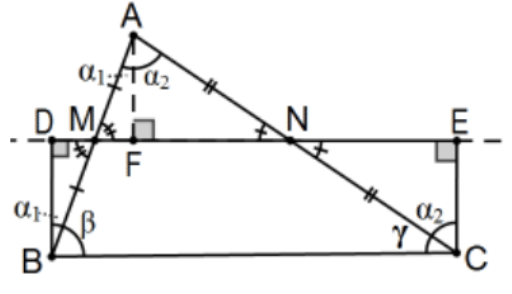
Prueba: La prueba más natural utiliza AAS al dejar caer la perpendicular de\(\mathrm{A}\)\(\mathrm{DE}\) a para determinar\(\mathrm{F}\) y concluir\(\mathrm{BD} \cong \mathrm{AF} \cong \mathrm{CE}\) que para que\(\mathrm{BD} \cong \mathrm{CE}\), el único detalle necesario para concluir\(\mathrm{BDEC}\) es Saccheri y la equivalencia de ese cuadrilátero con\(\triangle \mathrm{ABC}\) es obvia.
[Nota: Hay una prueba alternativa que usa SAS. Ver PS 2, #23.]
No obstante, la prueba no está completa porque no hemos discutido las sumas angulares. Además, incluso el resto de la prueba no está completa porque supone implícitamente que\(F\) cae entre\(M\) y\(N\) y que no tiene por qué ser así. Continuando con esa suposición, la conclusión de la suma de ángulos es fácil. Comenzando con los ángulos de cumbre, calculamos:
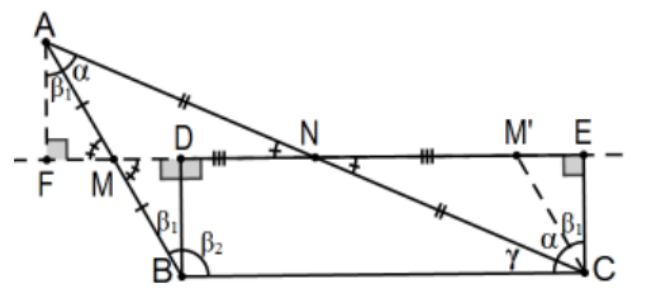
\(\left(\alpha_{1}+\beta\right)+\left(\gamma+\alpha_{2}\right)=\left(\alpha_{1}+\alpha_{2}\right)+\beta+\gamma=\alpha+\beta+\gamma\)según se requiera. Si bien la prueba anterior no es válida si\(\angle B\) es obtusa, el resultado sigue siendo cierto. En la figura indicada, deja\(\mathrm{M}^{\prime}\) ser el punto a lo largo del rayo\(\mathrm{NE}\) tal que se segmenta\(\mathrm{NM}^{\prime} \cong \mathrm{NM}\). Ahora\(\triangle \mathrm{ANM} \cong \triangle \mathrm{CNM}{ }^{\prime}\) por\(\mathrm{SAS}\) eso\(\mathrm{M}^{\prime} \mathrm{C} \cong \mathrm{MA}\) y, por suplementación,\(\angle \mathrm{CM}{ }^{\prime} \mathrm{E} \cong \angle \mathrm{AMF}\) para que\(\Delta \mathrm{CM}^{\prime} \mathrm{E} \cong \triangle \mathrm{AMF} \cong \triangle \mathrm{BMD}\) por\(\mathrm{AAS}\).
Esta vez\(\beta=\beta_{1}+\beta_{2}\) y, nuevamente comenzando por los ángulos de cumbre:
\(\beta_{2}+\left(\gamma+\alpha+\beta_{1}\right)=\alpha+\left(\beta_{1}+\beta_{2}\right)+\gamma=\alpha+\beta+\gamma\) QED.
Un cuadrilátero Lambert es un cuadrilátero con tres ángulos rectos. [En la Fig. \(\mathrm{ABCD}\), ángulos\(\mathrm{B}, \mathrm{C}\), y\(\mathrm{D}\) son ángulos rectos. ¿Cuál es el tamaño de\(\angle \mathrm{A}\)?]
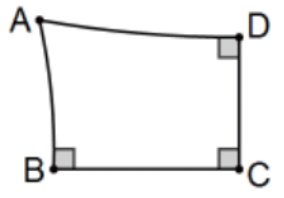
En un cuadrilátero Saccheri, la línea determinada por los puntos medios de la base y la cumbre determinan dos cuadriláteros Lambert congruentes.
Prueba: Ya está hecho a excepción del significado formal de polígonos congruentes. [Es decir, una distancia que preserva, el ángulo que preserva la transformación de todo el plano. La reflexión en esa línea de puntos medios proporciona la función de congruencia necesaria. QED.
Cada lado del cuarto ángulo de un cuadrilátero Lambert es mayor o igual a (es decir, no más corto que) el lado opuesto a él y su\(4^{\text {th }}\) ángulo no es obtuso.
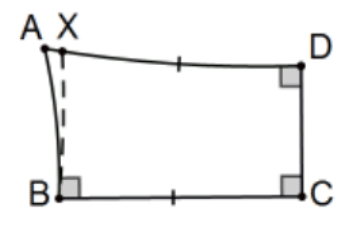
Prueba: Supongamos que ABCD es el cuadrilátero Lambert con ángulo desconocido A. Let\(X\) be along ray DA con segmento DX congruente al segmento\(C B\). Entonces la figura BCDX es un cuadrilátero Saccheri con cumbre\(\mathrm{BX}\). \(\angle \mathrm{XBC} \leq \angle \mathrm{ABC}\) así DX\(\leq\) DA (¿por qué?). QED.
La cumbre de un cuadrilátero saccheri es mayor o igual que su base y sus ángulos de cumbre no son obtusos.
Prueba: Estos son corolarios inmediatos a lo anterior (pero comienzan con un quad Saccheri, no un Lambert).
Estos cuadriláteros (ambos “casi” rectángulos) fueron estudiados extensamente por sus epónimos en un esfuerzo por probar el\(5^{\text {th }}\) Postulado de Euclides. Como se indica en este último teorema, cualquier cosa demostrable por un enfoque puede traducirse en una prueba del otro. El truco está en tener cuidado para comenzar por donde hay que empezar. Por ejemplo, en lo anterior, comience con un cuadrilátero general Saccheri; no empieces con un cuadrilátero Lambert. Otro ejemplo es que el cuarto ángulo de un cuadrilátero Lambert no es obtuso. Esta vez para demostrarlo, comenzar con un cuadrilátero general Lambert y construir un cuadrilátero saccheri útil.
Hay otros teoremas de geometría neutra que podrían probarse, especialmente aquellos que se pueden afirmar en esta forma “mayor que o igual a” pero que se expresarán sólo en su geometría hiperbólica forma “estricta” en el siguiente capítulo. Romperemos aquí y empezaremos a mirarlos desde esa perspectiva.