2.2: Conjunto de problemas 2

Última actualización
Guardar como PDF

Page ID: 118068

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Los exs 1-6 se refieren a las líneas ilustradas$\ell$ y$m$ que comparten una transversal que forma un par de ángulos interiores alternados congruentes,$\angle B A C \cong \angle A B D$. En cada caso, deje$\mathrm{M}$ ser el punto medio del segmento$\mathrm{AB}$ y deje$\mathrm{E}$ ser el pie de la perpendicular de$\mathrm{M}$ a$\ell$. Además, comience por hacer un boceto correspondiente toda la información dada de la manera estándar y, igualmente importante, nada más que la información dada. Luego demuestre que la línea resultante EF es una perpendicular común de las dos líneas libremente usando cualquiera de las declaraciones de congruencia estándar SAS, SSS, ASA, AAS o Hypotenuse-Leg según corresponda. [Supongamos que la línea AB no es perpendicular a la línea$\ell$ o ya hemos terminado!]

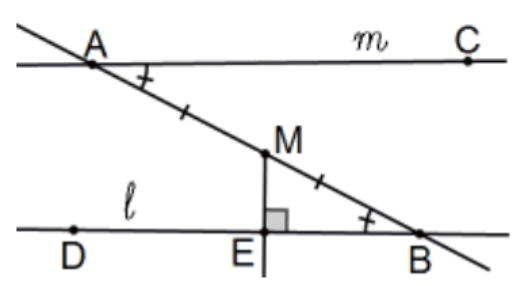
$Captura de pantalla 2022-06-23 en 1.19.17 PM.png$

Dejar$\mathbf{F}$ ser la intersección de la línea EM con$m$. [¡Suponiendo que sí se cruzan!]
Dejar$\mathrm{F}$ ser el pie de la perpendicular de$\mathrm{M}$ a$m$.

[Nota: No olvide mostrar que E, M y F son colineales.]

3. Dejar$\mathrm{F}$ ser el pie de la perpendicular de la A a la línea EM.

Deja$\mathrm{F}$ ser el punto junto$\mathrm{AC}$ con el rayo$\mathrm{AF} \cong \mathrm{BE}$.
Deja$\mathrm{F}$ ser el punto junto$\mathrm{EM}$ con el rayo$\mathrm{MF} \cong \mathrm{ME}$.
$\mathrm{F}$Sea la intersección (correcta) de los círculos (A; BE) y (M; ME); es decir, los círculos centrados en A de radio$\mathrm{BE}$ y en$\mathrm{M}$ de radio ME.

Nota: Es preferible usar menos símbolos pero palabras bien elegidas para declarar resultados matemáticos; se enfoca más en los conceptos en lugar de su presentación específica. Los Exs. 7-10 repiten cuatro de los Exs 1-6 exhibiendo esa filosofía.

7. Use SAS para probar que si una transversal a dos líneas forma un par de ángulos interiores alternados congruentes, entonces las líneas tienen una perpendicular común.

Usa ASA para demostrar que si una transversal a dos líneas forma un par de ángulos interiores alternados congruentes, entonces las líneas tienen una perpendicular común.
Use AAS para probar que si una transversal a dos líneas forma un par de ángulos interiores alternados congruentes, entonces las líneas tienen una perpendicular común.
Use SSS para probar que si una transversal a dos líneas forma un par de ángulos interiores alternados congruentes, entonces las líneas tienen una perpendicular común.
(En cierto sentido, lo contrario de cada una de estas 1-10) Demostrar que si una línea es una perpendicular común a otras dos líneas, cualquier transversal a las líneas que pasa por el punto medio del segmento determinado por la perpendicular común forma congruentes ángulos interiores alternos.

En Exs 12-16, asumen$\mathrm{ABCD}$ ser un cuadrilátero Saccheri con cumbre$\mathrm{AD}$ y demostrar que la línea MN es la bisectriz perpendicular tanto de la base como de la cumbre donde la nueva cifra está determinada por la información que se da en cada ejercicio. Incluya un boceto apropiado y competente para cada uno con toda la información dada indicada así como los puntos y segmentos auxiliares que utilice pero no indique ninguna información sobre ellos que deba probarse.

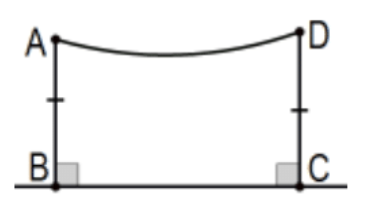
$Captura de pantalla 2022-06-23 en 1.23.31 PM.png$

12. $M$y$N$ son los puntos medios de la base y cumbre, respectivamente, de ABCD.

$M$es el punto medio de la base de$A B C D$ y$N$ está determinado por la perpendicular en$M .$ [Verbalmente, la bisectriz perpendicular de la base es también la bisectriz perpendicular de la cumbre.]
$\mathrm{N}$es el punto medio de la cumbre de$\mathrm{ABCD}$ y$\mathrm{M}$ está determinado por la perpendicular en$\mathrm{N}$. [Verbalmente, la bisectriz perpendicular de la cumbre es también la bisectriz perpendicular de la base.]
$\mathrm{N}$es el punto medio de la cumbre de$\mathrm{ABCD}$ y$\mathrm{M}$ es el pie de la perpendicular$\mathrm{N}$ a la base.
$M$es el punto medio de la base de$A B C D$ y$N$ es el pie de la perpendicular$M$ a la cumbre.

En los Exs 17-21, supongamos que ABCD es un cuadrilátero Lambert con cuarto ángulo a$A$ y demostrar que ABEF es un cuadrilátero Saccheri con línea de cumbre AD donde la nueva cifra está determinada por la información dada en cada ejercicio. Incluir un boceto apropiado y competente para cada uno con toda la información dada indicada y ninguna otra información señalada como dada.

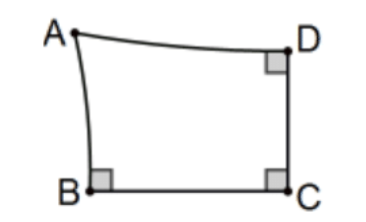
$Captura de pantalla 2022-06-23 en 1.25.26 PM.png$

17. $\mathrm{E}$es a lo largo de rayo$\mathrm{BC}$ con$\mathrm{CE} \cong \mathrm{BC}$ y$\mathrm{F}$ está junto$\mathrm{AD}$ con rayo con$\mathrm{DF} \cong \mathrm{AD}$. [Informalmente, doble cada uno de un par de lados opuestos.]

$\mathrm{E}$está a lo largo del rayo$\mathrm{BC}$ con$\mathrm{CE} \cong \mathrm{BC}$ y$\mathrm{F}$ está en el rayo perpendicular en$\mathrm{E}$ con$\mathrm{EF} \cong \mathrm{BA}$.
$\mathrm{F}$está a lo largo del rayo$\mathrm{AD}$ con$\mathrm{DF} \cong \mathrm{AD}$ y$\mathrm{E}$ es el pie de la perpendicular$\mathrm{F}$ a la línea$\mathrm{BC}$.
E está a lo largo del rayo$\mathrm{BC}$ con$\mathrm{CE} \cong \mathrm{BC}$ y$\mathrm{F}$ es la intersección de$(\mathrm{E} ; \mathrm{AB})$, el círculo centrado en$\mathrm{E}$ de radio$\mathrm{AB}$ y$(\mathrm{D} ; \mathrm{AD})$, el círculo centrado en$\mathrm{D}$ de radio AD. [Pista: Necesidad de mostrar DOS ángulos rectos.]
$\mathrm{F}$está a lo largo del rayo$\mathrm{AD}$ con$\mathrm{DF} \cong \mathrm{AD}$ y$\mathrm{E}$ es la intersección de$(\mathrm{F} ; \mathrm{AB})$, el círculo centrado en$\mathrm{F}$ de radio$A B$, y$(C ; B C)$, el círculo centrado en $C$de radio$B C$. [Pista: Necesidad de mostrar DOS ángulos rectos.]
$\mathrm{E}$está a lo largo del rayo$\mathrm{BC}$ con$\mathrm{CE} \cong \mathrm{BC}$ y$\mathrm{F}$ es la intersección de la perpendicular en$\mathrm{E}$ con la línea$A D$.
Dar una prueba alternativa del hecho de que el cuadrilátero de cualquier cuadrilátero Saccheri asociado de un triángulo es, de hecho, Saccheri de la siguiente manera. Comience como antes pero lleve$\mathrm{F}_{1}$ junto rayo$\mathrm{DM}$ con$\mathrm{MF}_{1} \cong \mathrm{MD}^{\mathrm{M}}$ y$\mathrm{F}_{2}$ junto rayo EN con$\mathrm{NF}_{2} \cong \mathrm{NE}$. Demostrar que$\mathrm{F}_{1}=\mathrm{F}_{2}=\mathrm{F}$, la perpendicular única de la línea A$\mathrm{MN}$ y concluir, como antes, que el cuadrilátero resultante BDEC es Saccheri con cumbre BC.
Demostrar que si los lados opuestos de un cuadrilátero son congruentes, la figura es un paralelogramo.
Demostrar que los lados opuestos de un cuadrilátero son congruentes si y sólo si sus diagonales se bisectan entre sí.
Demostrar que la bisectriz perpendicular de un lado del triángulo es perpendicular a la línea que une los puntos medios de los otros dos lados. [Pista: Piense en un cuadrilátero Saccheri asociado.]
Falta en la lista de teoremas de congruencia triangular SAS, SSS, ASA y AAS es ASS. Más allá de la falta de decoro, hay muy buena razón; la información es insuficiente para garantizar la congruencia a menos que se sepa que el ángulo es un ángulo recto en cuyo caso es cierto pero se llama “Hipotenusa-Pierna”. Mostrar con ejemplo explícito que existen dos triángulos no congruentes con las hipótesis de ASS satisfechas.
Claramente, el Teorema del Ángulo Exterior no se sostiene sobre una esfera (por ejemplo, dos líneas longitudinales a través del Polo Norte y el Ecuador). Explique dónde sale mal la prueba estándar del ángulo exterior (como debe). Incluye un buen boceto (es) para apoyar tu respuesta. Si puedes, caracterizar (es decir, encontrar condiciones necesarias y suficientes para) cuando sea válido. [Pista: Para fallar, el triángulo tiene que ser grande en algún sentido. ¿Cuál es ese sentido y qué tan grande es demasiado grande?]
Demostrar que la siguiente construcción para las tangentes a un círculo desde un punto fuera de un círculo al círculo es válida: Deje que el círculo se centre en$\mathrm{O}$ y deje$\mathrm{P}$ ser el punto fuera del círculo. Construya una tangente (si la hay) de P al círculo.

Construcción: Suponiendo que el centro O ha sido construido, deje que A sea la intersección del segmento OP con el círculo y construya la perpendicular a la línea OP en A. Construir círculo$(O ; O P)$, el círculo centrado en$O$ de radio OP y dejar$\mathrm{B}$ ser una intersección de esta línea y este círculo. Por último, deje$\mathrm{T}$ ser la intersección de$\mathrm{BO}$ con el círculo original. Reclamación: La línea PT es tangente al círculo original.

[Nota: Esta construcción es una construcción de geometría neutra pero en gran parte desconocida para los estudiantes de geometría estadounidenses en deferencia a una construcción estrictamente euclidiana (ver Chapt 4). Es un poco asombroso porque esta construcción viene antes en Euclides's Elements, ¡es más fácil, y su prueba es más fácil!]

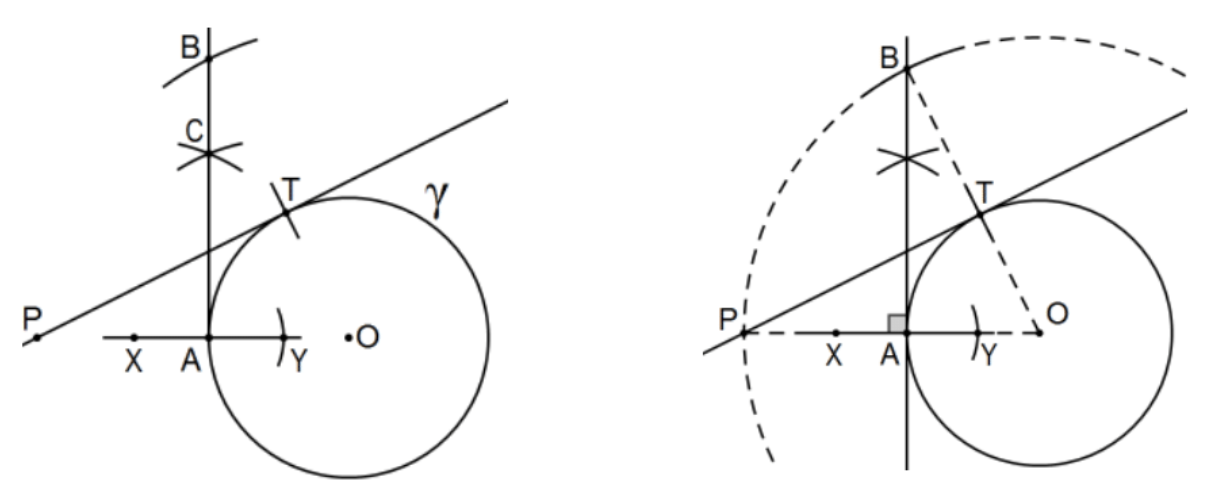
$Captura de pantalla 2022-06-23 en 1.28.56 PM.png$

30. Demostrar que la línea$\mathrm{PT}$ es la única tangente sobre$\mathrm{P}$ el círculo en el mismo lado de la línea del OP como punto B. [Pista: Dejar$S$ ser un punto en el círculo en el mismo lado de la línea$\mathrm{OP}$ como$\mathrm{T}$ tal esa línea $\mathrm{PS}$es tangente al círculo y probarlo$\mathrm{T}=\mathrm{S}$, de ahí exactamente una tangente a cada lado de la línea OP.]