3.1: Geometría Hiperbólica

Todo el resto de axiomas y definiciones (¡que siguen sin especificar!) de geometría neutra permanecen vigentes pero además añadimos:

Postulado Hiperbólico Paralelo (Forma Local)

Existe una línea y un punto no en esa línea tal que hay dos líneas en ese punto que son paralelas a la línea original.

Siempre es buena idea plantear la hipótesis lo menos posible pero este axioma a veces se afirma como:

Postulado Paralelo Hiperbólico (Forma Global)

Para cualquier línea y cualquier punto que no esté en esa línea, hay dos líneas en ese punto que son paralelas a la línea original.

Para mayor especificidad, dejar$\ell$ ser la línea y dejar$\mathrm{P}$ ser el punto no en la línea y dejar$m$ y$n$ ser dos líneas en P que son paralelas a$\ell$.

Teorema

Estos dos axiomas son equivalentes; es decir, uno es verdadero si y sólo si el otro es verdadero.

Prueba: Obviamente, el segundo implica el primero por lo que no hay nada que probar en esta dirección. Por el contrario, supongamos que la forma local es verdadera, digamos línea$\ell$ y punto$\mathrm{P}$ con$m$ y líneas$n$ distintas en P paralelas a$\ell$. Primero probamos un caso especial, múltiples paralelos en cualquier punto$P^{\prime}$ de la línea en$P$ perpendicular a$\ell$, digamos PF, donde$F$ está el pie de la perpendicular de P.

Caso 1: P'F > PF [Fácil.] Copia los ángulos en P determinados por$m$ y$n$ con la perpendicular at$\mathrm{P}^{\prime}$.

Caso 2: P'$\mathrm{F}<\mathrm{PF}$ [Mucho más difícil.] Dejar$m$ ser un paralelo a$\ell$ sobre P que no es perpendicular a PF. [No necesitaremos un segundo paralelo en P.] Centrándose en el lado agudo, dejar$\mathrm{M}$ ser el punto medio del segmento PF, y dejar que la línea$n$ sea la perpendicular a la línea PF en M. Primero construimos múltiples paralelos en$M$, no en$P^{\prime}$ y ya tenemos uno, a saber $n$. Surgen dos casos, o$m$ es paralelo$n$ o no lo es.

Caso 2a:$m \| n$.

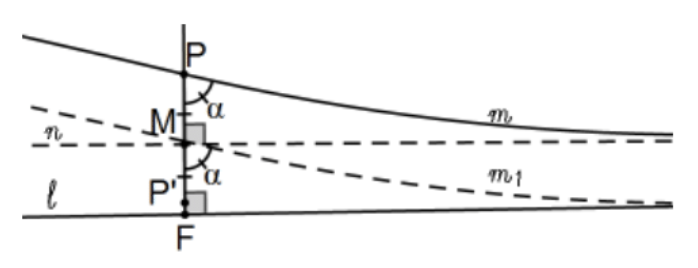
En este caso, copie el ángulo$\mathrm{P}$ con la perpendicular en$\mathrm{M}$ para obtener$m_{1}$ y usar ASA para Triángulos Largos. Entonces$m_{\uparrow}$ y$n_{n}$ son múltiples paralelos en$\mathrm{M}$.

Caso$2 \mathrm{~b}: m \cap n \neq \Phi$, digamos Q. Que R esté a lo largo del rayo PQ más allá de Q. Entonces la línea MR es otro paralelo a$\ell$ sobre M junto con$n$. ¿Por qué?

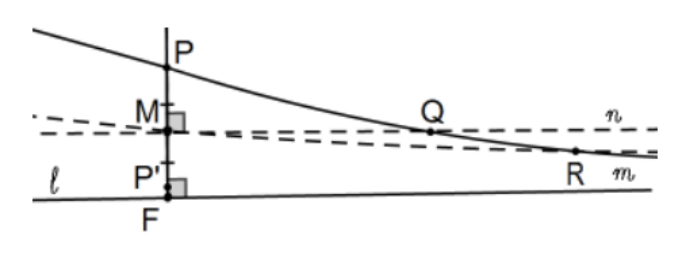
Entonces, cualquiera de los casos conduce a múltiples paralelos en$\mathrm{M}$ pero necesitamos múltiples paralelos en$\mathrm{P}^{\prime}$, no$\mathrm{M}=\mathrm{M}_{1}$. ¿Qué hacer? Repetir recursivamente hasta que el nuevo$M_{n}$ esté entre$F$ y$P^{\prime}$ (por la propiedad de Arquímedes de longitud) y use Caso$1 .$

Situación general para cualquier línea y punto no en ella? Usa ASA para Triángulos Largos de lo que ya se ha hecho. QED.

Teorema

No hay rectángulo (es decir, no cuadrilátero con cuatro ángulos rectos).

- [Nota: En nuestro “mundo real”, el mismo resultado es cierto. ¿No hay rectángulos? ¡¿Qué puede significar eso? Significa que no vivimos en un plano; vivimos en una esfera y no hay rectángulos en una esfera; de hecho, no hay paralelogramos o incluso trapecios. ¿Por qué no?]

Prueba: Supongamos por contradicción que ABCD es un rectángulo así que (por definición) cada uno de sus ángulos son ángulos rectos y (por teorema) ambos pares de lados opuestos son congruentes. Doblar la base y la cumbre; es decir, considerar$C_{1}$ de rayo$B C$ con$C_{1} \cong B C$ y$D_{1}$ de rayo$\mathrm{AD} \mathrm{DD}_{1} \cong \mathrm{AD}$. Renombrando$\mathrm{A}=\mathrm{A}_{0}, \mathrm{~B}=\mathrm{B}_{0}, \mathrm{C}=\mathrm{C}_{0}=\mathrm{B}_{1}$ y$\mathrm{D}=\mathrm{D}_{0}=\mathrm{A}_{1}$ (para establecer la inducción matemática natural que omitiremos), concluimos que$\mathrm{A}_{0} \mathrm{~B}_{0} \mathrm{C}_{0} \mathrm{D}_{0}$ y$\mathrm{A}_{1} \mathrm{~B}_{1} \mathrm{C}_{1} \mathrm{D}_{1}$ son cuadriláteros$\mathrm{congruent}$ Saccheri para que los ángulos en$C_{1}$ y $D_{1}$también son ángulos rectos y$A_{1} B_{1} C_{1} D_{1}$ es un rectángulo congruente con el rectángulo original$A B C D$. Múltiples paralelos en$A$ a línea$B C$ implica que hay un segundo paralelo a línea$B C$ en punto$A$ que forma un ángulo de medida$\alpha<90^{\circ}$ con la línea vertical$A B$ y dejar $\mathrm{E}=\mathrm{E}_{0}$ser la intersección de esa línea con$\mathrm{CD}$, el lado opuesto del rectángulo original. Que$\mathrm{E}_{1}$ se determine por esa línea con$\mathrm{C}_{1} \mathrm{D}_{1}$. Ahora vamos a$\mathrm{F}_{1}$ estar junto rayo$\mathrm{D}_{1} \mathrm{C}_{1}$ con$\mathrm{D}_{1} \mathrm{~F}_{1} \cong \mathrm{DE}($ segmentos de medida$\mathrm{x})$. Entonces$\mathrm{E}_{0} \mathrm{~A}_{1} \mathrm{D}_{1} \mathrm{~F}_{1}$ y$\mathrm{E}_{0} \mathrm{~B}_{1} \mathrm{C}_{1} \mathrm{~F}_{1}$ son cuadriláteros Saccheri con pares de ángulos de cumbre suplementarios en$\mathrm{E}_{0}$ y$\mathrm{F}_{1}$ que son congruentes por lo que son ángulos rectos por lo que estos cuadriláteros saccheri también son rectángulos. Por lo tanto,$\mathrm{E}_{0} \mathrm{~F}_{1} \cong \mathrm{A}_{1} \mathrm{D}_{1} \cong \mathrm{AD}$. Por el hecho de que$\mathrm{ABCD}$ es un rectángulo, el ángulo suma del cuadrilátero$\mathrm{ABCE}$ y$\triangle \mathrm{ADE}$ debe ser exactamente$360^{\circ}+180^{\circ}$ (los ángulos suplementarios en E) sin exceder ninguno de esos números. Esto implica$\angle \mathrm{BAE}$ y$\angle \mathrm{AEC}$ son complementarios y de ello se deduce$\angle \mathrm{DAE} \cong \angle \mathrm{F}_{1} \mathrm{E}_{0} \mathrm{E}_{1}$. Por ASA,$\triangle \mathrm{ADE} \cong \triangle \mathrm{E}_{0} \mathrm{~F}_{1} \mathrm{E}_{1}$ para$\mathrm{F}_{1} \mathrm{E}_{1} \cong \mathrm{DE}$ que$\mathrm{D}_{1} \mathrm{E}_{1}=\mathrm{x}+\mathrm{y}=2(\mathrm{DE})=2 \mathrm{x}$. Generalizando este proceso, tenemos$\mathrm{D}_{\mathrm{n}} \mathrm{E}_{\mathrm{n}}=(\mathrm{n}+1) \mathrm{x}=(\mathrm{n}+1) \mathrm{DE}$ para todos$\mathrm{n}$ y, para lo suficientemente grande$\mathrm{n}, \mathrm{nx}>\mathrm{AB}$ (por la propiedad arquímedea de longitud; es decir, suficientes copias de un segmento, no importa cuán corto sea, supera a otro, por mucho tiempo, una consecuencia del Gobernante Postulado.) Pero eso significa que$D_{n} E_{n}>D_{n} C_{n} \cong A B$ obligando$E_{n}$ a estar al otro lado de la línea$\mathrm{BC}$ y, por continuidad, líneas paralelas$\mathrm{AE}$ y se$\mathrm{BC}$ cruzan en algún lugar entre$\mathrm{A}$ y $\mathrm{E}_{\mathrm{n}}$, una contradicción obvia. El hipotético rectángulo original$\mathrm{ABCD}$ no existía. QED.

Corolario: Los ángulos de cumbre de un cuadrilátero saccheri son agudos.

Corolario: El 4º ángulo de un cuadrilátero de Lambert es agudo.

Corolario: La suma de los ángulos de un triángulo es menor que$180^{\circ}$ (un ángulo recto).

Prueba: Mira cualquiera de sus cuadriláteros Saccheri asociados. La suma de sus ángulos de cumbre... QED.

Nota

Estas consecuencias del HPP (y muchas otras) son en realidad equivalentes a ella.

Por ejemplo, supongamos en lugar del HPP, asumimos que hay un triángulo, digamos$\triangle \mathrm{ABC}$, con suma de ángulo$\alpha+\beta+\gamma<180^{\circ}$.

$A$En línea$A B$, y en el lado opuesto$\angle A B C$, copia$\angle B A D$, digamos$A C$, y$A$ en el lado opuesto, copia$\angle A C B$ para obtener$\angle C A E$. Mira las líneas$\mathrm{AD}, m$, y$\mathrm{AE}, n . \mathrm{So}$? QED.

Corolario: Cualquiera de los lados del$4^{\text {th }}$ ángulo de un cuadrilátero Lambert es mayor que el lado opuesto a él.

Prueba: A partir de geometría neutra, sabemos que es mayor o igual que el lado opuesto a ella. Si fueran "iguales” (congruentes), tendríamos un cuadrilátero Saccheri con 4 ángulos rectos. QED.

Corolario: La cumbre de un cuadrilátero saccheri es mayor que su base.

[Pista: Comenzando en la línea de puntos medios y “inclinando la cabeza$90^{\circ}$" de cualquier manera arroja un cuadrilátero Lambert con una cumbre del cuadrilátero Saccheri como$4^{\text {th }}$ ángulo.]

Corolario: El segmento lineal que une los puntos medios de la base y la cumbre de un cuadrilátero Saccheri es estrictamente más corto que cualquier otro segmento lineal desde su línea base hasta su línea de cumbre.

Corolario: Si dos líneas comparten una perpendicular común, ese segmento es más corto que cualquier otro segmento de línea de una a otra. [Es decir, no hay “vías del ferrocarril”.]

En geometría hiperbólica, las líneas paralelas no necesariamente tienen una perpendicular común. Si estuviéramos siendo formalmente axiomáticos, también tendríamos que estudiar los números reales desde esa perspectiva (incluso la teoría de conjuntos subyacente, ¡nunca terminaríamos!) pero uno de los axiomas definitorios que usaremos. Se le llama el “Axioma de Integridad de Número Real” y, en la forma que lo necesitamos, garantiza que cualquier subconjunto no vacío de los números reales que esté delimitado por debajo tenga un límite inferior mayor.

Límite (o Límite) Paralelo

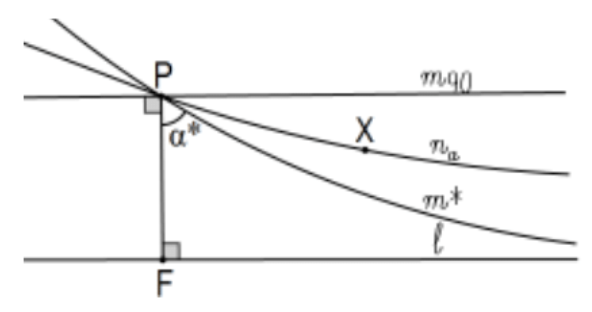
Para un punto P no en línea$l$, hay una línea paralela única$m^{*}$ (una en cada dirección) que minimiza el ángulo (en ese lado) hecho por líneas$P$ con la perpendicular que son paralelas a$l$. Este es el límite derecho (en la foto o la izquierda) o el límite paralelo.

[Nota 1: Algunos autores utilizan simplemente paralelo con el resto de ellos siendo llamados hiperparalelos.]

[Nota 2: Esto es un teorema así como una definición. Para ser matemáticamente “apropiada”, la existencia y singularidad de tal línea tendría que probarse primero y sólo entonces su definición tendría sentido. Procediendo hacia atrás...]

Prueba: Para cualquier línea$\mathrm{P}$ encendida, deje$\mathrm{F}$ ser el pie de la perpendicular$\mathrm{P}$ y considere el ángulo hecho en$\mathrm{P}$,$\angle \mathrm{FPX}$, donde$\mathrm{X} \neq \mathrm{P}$ está cualquier otro punto en la línea. Para$\alpha=\mathrm{m}(\angle \mathrm{FPX})$ (usando, grados, radianes, lo que sea), identificamos la línea como$m_{\alpha}$. Dependiendo del tamaño de$\alpha$, algunas líneas$m_{\alpha}$ son paralelas$l$ y otras no; es decir, algunas se cruzan$l$

Dejar que$\&=\left\{\alpha \mid m_{\alpha} \| \ell\right\} ;$ los ángulos determinados por los paralelos. $\&$no está vacío. ¿Por qué? & está “delimitado por debajo”. ¿Por qué? ¿Qué es un límite inferior mayor que$0^{\circ}$? ¿Por qué$\alpha=\mathrm{m}(\angle \mathrm{FPA})$ en esta cifra es un límite inferior para &? ¿Por qué hay un límite inferior mayor? Definimos el ángulo de paralelismo o ángulo límite o ángulo límite o ángulo crítico para ser el mayor límite inferior de$\&$. Es decir,$\alpha^{*}=g l b(\ell)$.

La prueba concluye confirmando que$m_{\alpha^{*}}$, la línea sobre la$\mathrm{P}$ que hace ángulo$\alpha^{*}$ con el rayo perpendicular$P F$, es paralela a$l$ lo que realmente$\alpha^{*}$ está adentro$\&$ y nosotros tener nuestro paralelo encendido$P$. Este hecho es inmediato a partir de la idea de la figura anterior; es decir, una línea en$P$ que se cruza$l$, la línea$P A$ determina un tamaño de ángulo ($\alpha)$en$P$ ese es un límite inferior para$S$ pero obviamente no es el mayor límite inferior. QED.

Teorema$\PageIndex{1}$

Las líneas que se cruzan divergen más rápido que proporcionalmente. Más específicamente, la distancia (BF en la figura) desde un punto en un lado de un ángulo al otro lado del ángulo (F) es más que duplicada (CF) si la distancia desde el vértice se duplicó. [Nota: Otra interpretación de esta afirmación sería duplicar segmentos en cada rayo y demostrar que el tercer lado del triángulo determinado está más que duplicado. Esto también es cierto aunque no lo necesitamos excepto en el contexto de desmentir el Teorema de Pitágoras (por si acaso$\angle A$ es un ángulo recto). [Ver PS 3, #18; la misma prueba funciona para cualquier$\angle A$.]

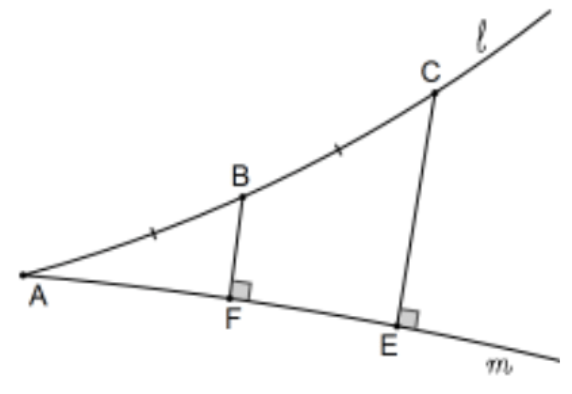
En primer lugar. ¿Qué se entiende por la distancia de un punto en una línea a otra línea? Como hemos visto antes, es la longitud del segmento perpendicular desde el punto hasta la línea. En la figura, las líneas$l$ y$A, B$ se$m$ cruzan en cualquier punto a lo largo de una de ellas,$C$ es tal que$B C \cong A B$ (segmento doble$A B$), y$F$ y$E$ son determinado por las perpendiculares a la otra línea de$B$ y$C$. En geometría euclidiana, AA Similaridad implicaría que$\mathrm{CE}=2(\mathrm{BF}) .$ En geometría hiperbólica, lo demostramos$\mathrm{CE}>2(\mathrm{BF})$.

Prueba: Copia$\angle A$ en$B$ para obtener$\angle C B D$ y dejar$G$ ser el pie de la perpendicular de$C$ a línea para$B D$ que$\triangle A B F \cong \triangle B C G$ por$\mathrm{AAS}$ y $\mathrm{CG} \cong \mathrm{BF}$por cpctc. Dejar$\mathrm{H}$ ser la intersección de$\mathrm{CE}$ con BD. Entonces$\mathrm{CH}$ está la hipotenusa del triángulo rectángulo$\triangle \mathrm{CHG}$. Para mayor claridad, deja$x=m(B F)$ y deja$y=m(C H)$. Ahora vamos a$\mathrm{J}$ estar a lo largo$\mathrm{EC}$ de rayo de longitud$\mathrm{x}$ para que$\mathrm{BFEJ}$ sea un cuadrilátero Saccheri. Dado que el original$\angle \mathrm{A}+\angle \mathrm{ABF}$ es menor que un ángulo recto,$\alpha+\beta<90^{\circ}$. Esto implica eso$\mathrm{E}, \mathrm{J}, \mathrm{H}$, y$\mathrm{C}$ están alineados correctamente en la imagen así$\mathrm{z}>0$ (¿por qué así?). Con eso,$x \leq y, 2 x<x+y+z$ así que eso$C E>2(B F)$.

Corolario: Si dos líneas comparten una perpendicular común, divergen en ambas direcciones.

Prueba: Supongamos que la línea AC es una perpendicular común a las líneas$\mathrm{AB}$$C D$ y y deja$C E$ ser otra paralela a la línea$A B$ que forma un ángulo agudo con la perpendicular AC. Por el teorema recién probado, las líneas CD y$C E$ divergen. Tanto más, CD y AB. Por simetría, lo mismo se aplica si el ángulo agudo está en el otro lado de AC. QED.

Nota

Esto dice más que eso las líneas se están separando más. Ese podría ser el caso de las líneas que se comportan asintóticamente. Esto dice que están arbitrariamente alejados; es decir, eventualmente superando cualquier distancia especificada.

Teorema de Congruencia AAA

Si dos triángulos...

Prueba: Copia una sobre la otra usando SAS Congruency y mira el cuadrilátero resultante. La suma de sus ángulos debe ser$360^{\circ}$ pero no existe tal. $\quad$QED.

Nota: La misma idea se sostiene sobre una esfera; es decir, en nuestro “mundo real”, dos triángulos con los tres ángulos congruentes por pares son triángulos congruentes. La prueba utiliza “superávit” para sustituir al “déficit” de$180^{\circ}$.

Hay otros teoremas que se pueden probar de la misma manera. Por ejemplo:

Teorema: Teorema de la cumbre: Si dos cuadriláteros saccheri tienen cumbres congruentes y ángulos de cumbre congruentes, entonces son congruentes.

Prueba: Copia una sobre la otra desde la cumbre hacia abajo. [PS 3, #19] QED.

Teorema: Si dos cuadriláteros Saccheri tienen bases congruentes y ángulos de cumbre congruentes, son congruentes.

Prueba: PS 3, #20. QED.

¿Y si algunas partes de un cuadrilátero Saccheri se cambian mientras que otras se mantienen fijas?

Teorema: Si se extienden las patas de un cuadrilátero Saccheri, entonces se aumenta la cumbre y se disminuyen los ángulos de cumbre. [Por implicación, la base no se modifica aquí.]

Prueba: Considera Saccheri Cuadrilátero ABCD con rayos BA y CD extendieron la misma distancia; es decir,$\mathrm{AA}^{\prime} \cong \mathrm{DD}^{\prime}$ por lo que$\mathrm{A}^{\prime} \mathrm{BCD}^{\prime}$ sigue siendo Saccheri.

Dejar$\alpha=\mathrm{m}(\angle \mathrm{A})$ y$\beta=\mathrm{m}\left(\angle \mathrm{A}^{\prime}\right)$. $2 \beta+2(180-\alpha)<360^{\circ}$Entonces para que$\beta<\alpha$ y los ángulos de cumbre se disminuyan estrictamente como afirma el teorema. ¿Por qué AD debe ser menor que$A^{\prime} D^{\prime}$? Porque alejándose simétricamente de la perpendicular de dos líneas que comparten una perpendicular común, ensancha la separación. Ya sabemos que divergen, pero esto dice que están divergiendo consistentemente al aumentar la distancia desde la perpendicular común. Que la línea MN sea la bisectrización perpendicular del segmento BC. Sabemos que esta línea biseca y es perpendicular a ambas cumbres de manera que, al dejar$\mathrm{X}$ estar a lo largo de rayo$\mathrm{N}^{\prime} \mathrm{A}^{\prime}$ con$\mathrm{N}^{\prime} \mathrm{X} \cong \mathrm{NA}, \mathrm{ANN}{ }^{\prime} \mathrm{X}$ es un cuadrilátero saccheri con$\angle \mathrm{NAX}$ agudo pero$\angle \mathrm{NAA}{ }^{\prime}$ obtuso. Por lo tanto, la imagen se dibuja correctamente; es decir,$\mathrm{X}$ está entre$\mathrm{N}^{\prime}$ y$\mathrm{A}^{\prime}$. QED.

El siguiente es un resultado similar al anterior pero con una prueba muy diferente:

Teorema: Si se extiende la base de un cuadrilátero Saccheri, entonces se aumenta la cumbre y se disminuyen los ángulos de cumbre. [Por implicación, la longitud de las piernas no cambia.]

Prueba: Primero tenga en cuenta que hay tres cuadriláteros saccheri involucrados, los dos que estamos comparando y la extensión misma. Esta prueba se basa en señalar que dos ángulos adyacentes (en la figura,$\angle \mathrm{ADC}$ y$\angle \mathrm{D}^{\prime} \mathrm{DC}$) son cada uno agudos, así que juntos menos de un ángulo recto de modo que$\triangle \mathrm{ADD}^{\prime}$ es un triángulo genuino que obliga a E a colocarse correctamente (no fuera de$D$ a lo largo de ray CD). Eso implica que cumbre$\angle B \mathrm{BD}^{\prime}$ es menor que la cumbre original$\angle \mathrm{BAD}$ verificando la segunda conclusión del teorema. El mayor ángulo de$\triangle \mathrm{ADD}^{\prime}$ es$\angle \mathrm{D}$ así que el lado más grande es$\mathrm{AD}^{\prime}$ y la cumbre del nuevo cuadrilátero es mayor que la antigua cumbre, AD. QED.

Nota: Recordemos que la cumbre de un cuadrilátero Saccheri es paralela a la base pero, al “estirar la base”, siempre hay otra línea paralela a la base que hace un ángulo menor con la pata del cuadrilátero Saccheri desde ese punto (es decir, simplemente estirar la base un poco más). Esto confirma que el ángulo formado por la cumbre de un cuadrilátero Saccheri nunca es el ángulo crítico con una pata como las perpendiculares a su base.

Teorema: Si dos triángulos tienen la misma suma angular, entonces son equivalentes. [Converse de...]

Prueba: En resumen, primero probamos el caso en el que los triángulos tienen un lado de longitud común y luego forzamos hábilmente ese caso usando el siguiente lema (geometría neutra).

Lema: Si una línea que biseca un lado de un triángulo es perpendicular a la bisectriz perpendicular de un segundo lado, entonces biseca el tercer lado.

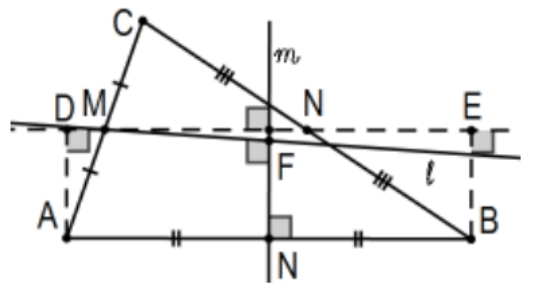
Prueba: En triángulo dado$\triangle \mathrm{ABC}$, dejar$\mathrm{M}$ ser el punto medio de$\mathrm{AC}$, dejar$m$ ser la bisectriz perpendicular de$\mathrm{AB}$, y dejar$\mathrm{F}$ ser el pie de la línea$\ell$ en $\mathrm{M}$perpendicular a$m$. Dejar$\mathrm{N}$ ser el punto medio del tercer lado BC y considerar el cuadrilátero Saccheri asociado ADEB. Su cumbre es$\mathrm{AB}$ y sabemos que la bisectriz perpendicular de la cumbre es perpendicular a su línea base MN. Así$l=$ MN. ¿Por qué? QED.

Caso 1: Los dos triángulos tienen un par de lados de la misma longitud.

Sin pérdida de generalidad, podemos suponer que un lado está superpuesto al otro como se muestra aquí (copia un triángulo sobre el otro si no está ya así posicionado).

Prueba: En la figura dada, asumir que$\triangle \mathrm{ABC}$ y$\triangle \mathrm{ABD}$ tener la misma suma angular y considerar sus cuadriláteros Saccheri asociados en el lado común AB. Por teorema anterior, sus ángulos de cumbre tienen la misma suma que los propios triángulos por lo que los dos cuadriláteros Saccheri tienen la misma cumbre AB y ángulos de cumbre congruentes así que, por el Teorema de la Cumbre, los son iguales para que$\triangle \mathrm{ABC} \sim \mathrm{AEFB} \sim \triangle \mathrm{ABD}$.

Nota: Incluso en este caso, producir la equivalencia concreta es más difícil de lo que parece. Recuerde que la equivalencia$\triangle \mathrm{ABC}$ de$\mathrm{AEFB}$ se muestra dejando caer la perpendicular de$\mathrm{C}$ a línea$\mathrm{MN}$ y de manera similar para$\triangle \mathrm{ABD}$ de$\mathrm{D}$ a línea$\mathrm{M}^{\prime} \mathrm{N}^{\prime}$, la misma línea $\ell$. La idea es hacer un seguimiento de ambos conjuntos de cortes ya que los triángulos se cortan dos veces, primero para reorganizar$\triangle \mathrm{ABC}$ para obtener$\mathrm{AEFB}$ y luego reorganizar de nuevo para obtener$\triangle \mathrm{ABD}$. Suena fácil pero...

Caso 2: El caso general. La idea es reducir el Caso 2 al Caso 1. Si los triángulos no son triángulos equiláteros congruentes, hay un lado de uno de ellos mayor que algún lado del otro o, por SSS, serían congruentes.

En$\triangle \mathrm{ABC}$ y$\triangle \mathrm{DEF}$, asumir sólo que tienen la misma suma de ángulo y$\mathrm{AC}<\mathrm{DF}$. (Ninguna correspondencia vértice por vértice es necesaria ni implícita). Consideremos el cuadrilátero Saccheri asociado para$\triangle \mathrm{ABC}$ con cumbre en cualquiera de los otros dos lados; elegimos$\mathrm{AB}$ así que$\mathrm{AGHB}$ es su cuadrilátero Saccheri asociado con base en línea MN, la línea de puntos medios. Dejar$P$ ser el punto medio del segmento$\mathrm{DF}$ y dejar$\mathrm{P}^{\prime}$ ser cualquiera intersección de círculo$(\mathrm{A} ; \mathrm{DP})$ (es decir, centro en$A$ y radio$\left.\mathrm{DP}\right)$, y línea$\mathrm{MN}$. [Obsérvese que$(1 / 2) \mathrm{AC}<(1 / 2) \mathrm{DF}$ así sí se cruzan]. Doble segmento$\mathrm{AP}^{\prime}$ a lo largo del rayo$\mathrm{AP}^{\prime}$ para determinar$\mathrm{F}^{\prime}$ así, por construcción,$A F^{\prime} \cong D F$. Dejar$Q$ ser la intersección de segmento$\mathrm{BF}^{\prime}$ y línea$M N$, y dejar$m$ ser la línea de puntos medios de la base y cumbre de Saccheri cuadrilátero AGHB; es decir, la perpendicular común. Considerando$\triangle \mathrm{ABF}^{\prime}$, señalar que$\mathrm{P}^{\prime}$ es el punto medio de lado$\mathrm{AF}^{\prime}$ y$m$ es la bisectriz perpendicular del lado AB así, ya que la línea MN es una perpendicular desde el punto medio de un lado de un triángulo a la bisectriz perpendicular de un segundo lado, su intersección con el tercer lado es el punto medio de ese lado por lo que$Q$ es el punto medio del tercer lado$\mathrm{BF}^{\prime}$ (por el Lema). Así línea no$\mathrm{MN}$ es solo una línea de puntos medios de$\triangle \mathrm{ABC}$, es una línea de puntos medios de así$\triangle \mathrm{ABF}^{\prime}$ así que también$\mathrm{AGHB}$ es su cuadrilátero Saccheri asociado con cumbre AB y la suma de los ángulos de cumbre es la suma de los ángulos de ambos$\triangle \mathrm{ABC}$ y$\triangle \mathrm{ABF}{ }^{\prime}$. Ahora$\triangle \mathrm{ABF}$ y$\triangle \mathrm{DEF}$ satisfacer las condiciones del Caso 1 porque$\triangle \mathrm{ABF}^{\prime}$ tiene la misma suma angular y comparte una longitud lateral con$\Delta \mathrm{DEF}$$\left(\mathrm{AF}^{\prime} \cong \mathrm{DF}\right) .$ Así$\triangle \mathrm{ABC} \sim \Delta \mathrm{ABF}^{\prime} \sim \Delta \mathrm{DEF}$ QED.

Nota

En este caso, producir la equivalencia concreta es mucho, mucho más difícil. ¿Por qué es eso? La nota posterior al Caso 1 describe cómo efectuar esto para$\triangle \mathrm{ABC} \sim \triangle \mathrm{ABF}^{\prime}$ y también para$\triangle \mathrm{ABF}^{\prime} \sim \triangle \mathrm{DEF}$ pero, por tedioso que sea, todavía parece ser engañosamente fácil. La dificultad es que el cuadrilátero saccheri para la primera equivalencia se basa en la cumbre común$\mathrm{AB}$ pero para el segundo es el cuadrilátero saccheri de$\triangle \mathrm{ABF}{ }^{\prime}$ con cumbre AF' tan diferente (pero, por supuesto, equivalente) cuadriláteros saccheri. Hacer un seguimiento de ambos conjuntos de cortes en el intermedio$\triangle \mathrm{ABF}^{\prime}$ y cómo se van a reorganizar para ir directamente de$\triangle \mathrm{ABC}$ a ¡$\triangle \mathrm{DEF}$está más cerca de un rompecabezas de 1,000 piezas que las matemáticas!

Si aún no lo hemos hecho para cuando lleguemos a este punto del curso, es momento de empezar a mirar un modelo de esta geometría para asegurarnos de que no estamos construyendo un bonito castillo en el cielo. Hay varios estándar pero el único con el que trabajaremos es el modelo de disco Poincaré para geometría hiperbólica:

$\mathcal{l}=(\rho, L, \varrho)$donde:

$\mathcal{P}$, el conjunto de puntos, es el conjunto de puntos interiores de un círculo euclidiano fijo$\gamma$ centrado en$\mathrm{O}$

$\mathcal{L}$, el conjunto de líneas, es el conjunto de diámetros (intervalo abierto) y arcos (abiertos) de círculos ortogonales; es decir, el arco interior de cualquier círculo euclidiano que se cruza de$\gamma$ manera que su tangente en el punto de intersección con el círculo sea perpendicular a la del círculo definitorio en punto, y

$\complement$, el conjunto de círculos, es el conjunto de círculos euclidianos que se encuentran completamente dentro del círculo definitorio$\gamma$.

Nota 1: Llamar a tal conjunto un círculo Poincaré es prematuro ya que “círculo” se define como el conjunto de todos los puntos a cierta distancia fija, llamada su radio, desde algún punto fijo, llamado su centro. Esto es prematuro ya que aún no hemos definido la distancia en esta geometría pero es muy útil para tratar de entender la geometría. El problema se resolverá en el Capítulo 5. No olvides que el centro de un círculo no es parte (un elemento) de un círculo, solo de su interior o que su centro Poincaré no necesita ser el mismo que su centro euclidiano.

$\underline{\text { Note 2: Lines determined by orthogonal circles always "curve away" from the center of the defining circle. }}$Esto es fácil de ver al notar que el triángulo formado por los dos centros circulares y cualquiera de los puntos de intersección es un triángulo rectángulo (por ortogonalidad) siendo el segmento de centros la hipotenusa tan más largo que el radio del círculo definitorio por lo que el segundo centro debe estar fuera de el círculo definitorio.

En esta figura, anotar los múltiples paralelos sobre$\mathrm{P}$ las líneas$\mathrm{AB}$ y$\mathrm{AO}$. Es decir, la línea PH es obviamente paralela a las líneas$\mathrm{AB}$ y$\mathrm{AO}$ pero también lo es PA ya que A, el punto de tangencia euclidiana, no es un punto en el plano Poincaré. PA es un límite paralelo a ellos. De manera similar, la línea PD es el otro límite paralelo en P a línea$A B$ y$P G$ es otro paralelo no límite en$\mathrm{P}$ la línea$\mathrm{AB}$. El pie de la perpendicular de$\mathrm{P}$ a línea$\mathrm{AB}$ es$\mathrm{F}$. Por razones aún no comprobadas,$\angle \mathrm{APF} \cong \angle \mathrm{BPF}$. Hay mucho que hacer para demostrar formalmente que esto realmente es un modelo para la geometría hiperbólica pero lo es. En esencia, este hecho es un teorema, que la geometría hiperbólica es “tan buena” como la geometría euclidiana. Es decir, si alguna vez surgiera una inconsistencia en la geometría hiperbólica, podría traducirse de nuevo en una inconsistencia en nuestra geometría euclidiana de confianza. Formalmente, la geometría hiperbólica es “relativamente consistente” con la geometría euclidiana; es decir, si los axiomas de la geometría euclidiana son consistentes, también lo son los de la geometría hiperbólica. Lo contrario también es cierto pero no vamos a estar mirando ese hecho.

Además, recordar y/o aprender la geometría euclidiana suficiente para comprender la esencia de esta prueba ocupará la mayor parte de la última parte del curso. Existe un enfoque sofisticado que clava el resultado casi como una ocurrencia posterior; el mapeo conformacional de transformaciones fraccionarias lineales en análisis complejos:

http://www.mathpages.com/home/kmath464/kmath464.htm

En general,$\mathrm{f}(\mathrm{z})=(\mathrm{az}+\mathrm{b}) /(\mathrm{cz}+\mathrm{d})$ pero, en nuestro caso, con$\mathrm{a}=\mathrm{d}=0, \mathrm{~b}=\mathrm{R}^{2}$, y$\mathrm{c}=1$ seguido de una reflexión en el eje real; es decir, conjugación. QED? No, ya que no se asumirá un análisis complejo. (¡¿No te alegro?!) Las ideas detrás de una prueba estrictamente geométrica requieren mucha geometría euclidiana, algunas de las cuales has visto pero gran parte de la cual no la has visto. Por ejemplo, las medidas de ángulos en este modelo son bastante obvias. Al igual que en el cálculo, son solo los ángulos entre sus tangentes en los puntos de intersección. La distancia es nueva.

La distancia Poincaré entre dos puntos (longitud de su segmento Poincaré) es el valor absoluto del logaritmo natural de la relación cruzada (euclidiana) de los dos puntos y los dos puntos que determina el círculo euclidiano de su línea. $$\mathrm{d}_{\mathrm{p}}(\mathrm{A}, \mathrm{B})=|\ln (\mathrm{A}, \mathrm{B} ; \mathrm{P}, \mathrm{Q})| \nonumber$$

El valor absoluto y los logaritmos naturales son familiares. Para cualquier punto$A, B, C$, y$D$, donde$A=B$ sea posible pero todos los demás son distintos), la relación cruzada de$A, B, C$, y D (en este orden) es:

$$(A, B ; C, D)=\frac{A C / C B}{A D / D B}=\frac{(A C)(D B)}{(A D)(C B)} \nonumber$$

Nota

En algunas aplicaciones, estas medidas de segmentos de línea euclidianos son medidas firmadas.

Pero ¿qué son$P$ y$Q$? Estos son fáciles asumiendo que cree que Axioma 1 es cierto en el modelo de disco de Poincaré para geometría hiperbólica; es decir, dos puntos determinan una línea. Suponiendo que como hecho (es decir, que dos puntos y la ortogonalidad con el círculo definitorio determinan un círculo o diámetro euclidiano único (ambos representados aquí), estos son los dos puntos de intersección de ese círculo o línea con el círculo definitorio. ¡Podrías objetar, aseverando que esos puntos no son interiores! Estarías en lo cierto ya que te estabas equivocando. Son perfectamente buenos puntos euclidianos y todo en la definición y en las pruebas están en geometría euclidiana; de hecho, esa es la idea. El modelo Poincaré para geometría hiperbólica está construido completamente dentro de la geometría euclidiana con líneas y círculos euclidianos y tenemos todo el plano euclidiano en el que trabajar. Si se están utilizando medidas firmadas, asigne una dirección positiva en cada línea y, para puntos$A$ y$B$ en una línea, si$A B$ (la medida del segmento de línea$\mathrm{AB}$) es positiva, entonces BA tiene el mismo valor absoluto pero es negativo.

Antes de estudiar más cuidadosamente el modelo de disco de Poincaré, desarrollaremos algunas ideas más únicas de la geometría hiperbólica. Eso no es del todo cierto. Los siguientes tres teoremas son ciertos en la geometría euclidiana; es solo que no son interesantes en ese caso ya que ese ángulo en cuestión siempre es solo un ángulo recto. Acostumbrarse a que no sea necesariamente un ángulo recto puede ser un desafío para algunos estudiantes.

Teorema

Los ángulos izquierdo y derecho de paralelismo (ángulo crítico) ángulo crítico en un punto definitorio P a una línea definitoria$l$ son los mismos por lo que, en adelante, "el ángulo de paralelismo”; es decir, no calificado en cuanto a izquierda o derecha.

Prueba: Deje que$n=$ PB sea el paralelo a la línea$\ell$ determinado por el ángulo crítico izquierdo de tamaño$\beta^{*}$ con la perpendicular en$\mathrm{P}, \mathrm{PF}$, y deje que el$m *=$ PA sea determinado por el ángulo crítico derecho de tamaño $\alpha^{*}$con el mismo PF perpendicular. Copia$\angle \mathrm{FPB}$$\mathrm{P}$ en el otro lado como se indica para establecer$\angle \mathrm{FPB}^{\prime}$ y alinear$n *^{\prime}$. Esa línea debe ser paralela por ASA para Triángulos Largos y por lo tanto$\alpha^{*} \leq \beta^{*}$ ya que es$\alpha^{*}$ un límite inferior para todos los paralelos a$\ell$ la derecha en$P$. No obstante, no había nada de especial en comenzar con la copia$\angle \mathrm{FPB}$. Copiar$\angle \mathrm{FPA}$ en el otro lado implica eso$\beta^{*} \leq \alpha^{*}$. Es decir, ambos$\alpha^{*} \leq \beta^{*}$ y$\beta^{*} \leq \alpha^{*}$ así tenemos igualdad. QED.

Más sorprendente, quizás, es que esta propiedad no depende del punto P. Eso puede resultar confuso sino que simplemente significa que el límite paralelo en otros puntos a lo largo de la misma línea es exactamente la misma línea:

Teorema$\PageIndex{1}$

Un límite (límite) paralelo$m *$ es un límite paralelo a la línea a$l$ en cada uno de sus puntos, no solo su punto definitorio P. [Nota: Esto implica que no debe llevar$\alpha^{*}$ como parte de su nombre.]

Prueba: Caso 1: Q$m *$ en el lado agudo de P. En este caso, deje caer la perpendicular a$l$$E$, digamos, y considere cualquier rayo desde$Q$ el interior del ángulo determinado con el límite paralelo, digamos $\varepsilon>0$. $A$Sea cualquier punto sobre este rayo y considere ray PA. Este rayo debe cruzarse$l$. ¿Por qué? Por lo tanto así debe ray QA. ¿Por qué? Este nuevo ángulo de paralelismo en$Q$ es estrictamente mayor que el de$P$. ¿Por qué? [PS 3, #13.]

Caso 2: Q sobre$m_{*} *=$ PA en el lado obtuso de P. Suelta la perpendicular para obtener$E$, y nuevamente considerar cualquier rayo desde$Q$ el interior de$\angle E Q P$, digamos rayo$\mathrm{QB}$, y el ángulo que determina con el límite paralelo, $\mathrm{m}(\angle \mathrm{PQB})=\varepsilon>0$. Copia ese ángulo como ángulo correspondiente$P$ formando un ángulo con rayo PF de tamaño$\alpha^{*}-\varepsilon<\alpha^{*}$, el ángulo de paralelismo, por lo que este rayo debe intersectar la línea original$l$ para que el rayo$Q B$ paralelo también la cruce. Dado que el rayo$Q B$ fue arbitrario, el ángulo con la perpendicular es el ángulo de paralelismo en$Q$. Consistente con el Caso 1, este nuevo ángulo de paralelismo$Q$ es menor que$\angle \mathrm{FPA}$. QED.

Teorema

Un límite (límite) paralelo está limitado por la distancia desde la distancia desde el punto definitorio hasta la línea definitoria.

Nota

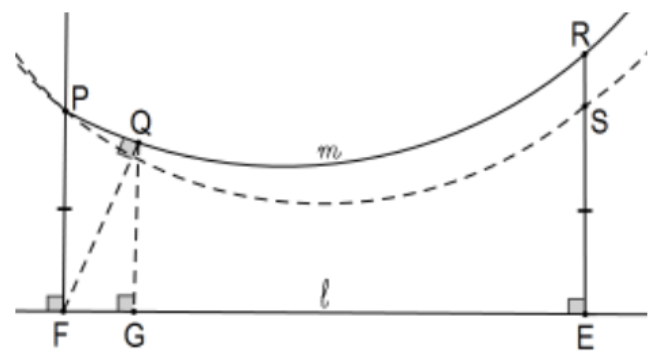
Obviamente, sólo estamos mirando al lado del ángulo agudo con la perpendicular. A lo largo, deja$\ell$ ser la línea, deja$\mathrm{P}$ ser el punto no encendido$\ell$, deja$\mathrm{F}$ ser el pie de la perpendicular de$P$ a$\ell$, y deja$m$ ser cualquier línea en $P$que forma un ángulo agudo con la perpendicular, paralela o no. Primero tenga en cuenta que (para cierta distancia) la distancia a$\ell$ desde un punto$m$ es estrictamente menor que la distancia de$\mathrm{P}$ a$\ell$. Para ver esto, deja$\mathrm{Q}$ ser el pie de la perpendicular de$\mathrm{F}$ atrás a la otra línea$m$ y luego dejar que$\mathrm{G}$ sea el pie de la perpendicular de nuevo a$l$. Considerando los triángulos rectos determinados y sus hipotenusas, claramente$\mathrm{QG}<\mathrm{QF}<\mathrm{PF}$. Podemos repetir esto ad infinitum pero eso no quiere decir que todos los segmentos sean siempre más cortos; por ejemplo, considere cualquier cuadrilátero Saccheri y la línea de puntos medios de su base y cumbre.

Prueba: Asumiendo solamente que tal$m$ en P no está acotada, mostramos que no$m$ es un límite paralelo a$\ell$; es decir, el contrapositivo. Suponiendo que esto no$m$ esté acotado equivale a asumir un punto sobre él, digamos R, tal que la distancia a$l$ sea mayor que la distancia a$P$. Es decir, si$E$ es el pie de la perpendicular, entonces$\mathrm{RE}>\mathrm{PF}$. Por el Postulado Gobernante, hay un punto$\mathrm{S}$ a lo largo del rayo ER tal que$\mathrm{ES} \cong \mathrm{FP}$. Pero entonces PFES es un cuadrilátero Saccheri con PS de cumbre; es decir, una línea paralela en P que hace un ángulo menor$\angle F P R$ que para que ese ángulo no fuera un límite inferior para todos los ángulos con la perpendicular en P que determinan líneas paralelas. Es decir, no$m$ es un límite paralelo a$\ell$. QED.

Teorema (Converse)

Si dos líneas paralelas están delimitadas (en una dirección), entonces son paralelos de límite entre sí.

Prueba: Si dos líneas se cruzan, sabemos que divergen en ambos sentidos. Supongamos$\ell$ y$m$ están delimitados en la dirección indicada en la figura,$\mathrm{P}$ es un punto sobre$m$, y$\mathrm{F}$ es el pie de la perpendicular de$\mathrm{P}$ a$l$. Por último, deja$n$ ser cualquier línea sobre la$\mathrm{P}$ que forme un ángulo con la perpendicular dentro del ángulo formado por$m$. Basta con mostrar que se$n$ cruza$l$. Desde$m$ y se$n$ cruzan en$\mathrm{P}$, divergen por lo que la amplitud de$m$ a$l$ obliga al resultado deseado. QED.

Teorema$\PageIndex{1}$

Suponiendo que un límite paralelo se define como un límite paralelo a sí mismo, el paralelismo límite es una relación de equivalencia (en la misma dirección de la delimitación, por supuesto).

Prueba:

Reflexivity: Verdadera por definición.

Simetría: Ya sabemos que un límite (límite) paralelo$m$ se limita a la línea definitoria$\ell$ independiente del punto que la determinó y que los paralelos que no están acotados (en la dirección aguda) comparten una perpendicular común por lo que divergen en ambas direcciones. Basta con saber que la línea definitoria$\ell$ está delimitada a ese límite (límite) paralelo$m$. Supongamos que no fuera así. Entonces quedaría sin límites en esa dirección y, como antes, determinaría un cuadrilátero saccheri con cumbre y base que divergiría en ambos sentidos; una contradicción.

Transitividad: Supongamos que$m$ es un límite paralelo a$\ell$ y$n$ es un límite paralelo a$\ell$. En caso$m$ o$n$ es entre$l$ y el otro, ese paralelo se “aprieta” entre dos que están acotados entre sí por lo que el único caso de interés es cuando$\ell$ está entre$m$ y $n$. En la figura, supongamos que ese es el caso con$P \in m$. Dejar$F$ ser el pie de la perpendicular a$l$ y dejar$Q$ ser la intersección de la línea PF con$n$. Que PF se cruza$n$ en absoluto no es tan obvio como podría buscar una muy buena razón; ¡no tiene por qué ser verdad! Eso es lo que$R G$ está haciendo el segmento de línea en la figura; parece irrelevante. Si el rayo$\mathrm{RG}$ no logra cruzarse$n$, elija cualquier punto$\mathrm{Q} \in n$,$\mathrm{F}$ repita, y elija entre$\mathrm{G}$ y$\mathrm{F}$ dependiendo de cuál esté más adelante en la dirección de la amplitud, como $F$está en la figura. Entonces el rayo QF debe cruzarse$m$, digamos$P$, debido a la delimitación a$l$. Dejando caer la perpendicular de$Q$ a$m$, tenemos un triángulo rectángulo$\triangle \mathrm{QEP}$ con$\mathrm{PQ}$ la hipotenusa así$\mathrm{QE}<\mathrm{PF}+\mathrm{FQ}$. Este argumento se puede aplicar a cualquier punto a la derecha de por$Q$ lo que$n$ está limitado hacia$m$ por segmento de línea$P Q$. De ahí que, por lo anterior, se limiten entre sí.

Teorema

Los paralelos fronterizos son asintóticos.

Prueba: Dejar$m_{u} *$ ser un límite (límite) paralelo a la línea$\ell$.

Demostramos que finalmente$m *$ está limitado (en la dirección del ángulo agudo) por cualquier distancia$\varepsilon>0$. Dejar$\varepsilon>0$ ser arbitrario y dejar$\mathrm{P}$ ser un punto de$m *$ y$\mathrm{F}$ es el pie de la perpendicular. Dejar$Q$ ser un punto junto$F P$ con rayo$m(F Q)=F Q=\varepsilon$. Por el resultado de la amplitud, no hay nada que probar si es$\varepsilon \geq \mathrm{FP}$ así asumir que$\varepsilon<F P$; es decir,$\mathrm{Q}$ está entre$\mathrm{F}$ y$\mathrm{P}$ como se muestra y dejar que$n *$ sea el límite paralelo a $l$$\mathrm{Q}$en sentido contrario. Es decir, si el ángulo agudo a$P$ es hacia la derecha, entonces el ángulo agudo a$Q$ es hacia la izquierda. Dado que$m *$ está delimitada hacia la línea$\ell$ y no$n *$ está delimitada en esa dirección, deben cruzarse; digamos en R. Luego duplicar el segmento a$Q R$ lo largo del rayo$P R$ para obtener$S$; i.e., $R S \cong R Q$. Reclamación:$m *$ está delimitada por$\varepsilon$ a la derecha de S. Para probar esto, deje$E$ ser el pie de la perpendicular sobre$\mathrm{S}$ y probar que de$\mathrm{ES} \cong \mathrm{FQ}$ manera que$m *$ quede acotada a la derecha de SE por $\varepsilon$. ¿El enfoque? $G$Dejen estar el pie de la perpendicular$R$ y probarlo$\triangle \mathrm{QFG} \cong \triangle \mathrm{SEG}$. [No es difícil pero es un poco complicado. Por qué es$\triangle \mathrm{QRG} \cong \triangle \mathrm{SRG} ?]$ QED.

En resumen, dos líneas son paralelismos límite si y sólo si no comparten una perpendicular común si y sólo si están delimitadas entre sí si y sólo si son asintóticas entre sí. Para ver estos teoremas en acción, mira hacia atrás a la figura asociada a la presentación del modelo de disco de Poincaré para geometría hiperbólica, a menudo simplemente el modelo de Poincaré aunque dio otro modelo para geometría hiperbólica. [Ese modelo usa un medio plano abierto en lugar de un disco para el conjunto de puntos. La mitad superior (abierta) del$x y$ plano es el conjunto de puntos, las líneas son rayos verticales (abiertos) y semicírculos (abiertos) ortogonales al eje X, y los círculos son círculos euclidianos que se encuentran completamente en el conjunto de puntos. Para su propia diversión, identifique paralelos que no sean paralelos de límites, paralelos de límites y ángulos de paralelismo izquierdo y derecho.]

Teorema

Existen triángulos que no se pueden circunscribir.

Prueba: Es decir, producir uno. Mostramos una manera de producir ejemplos:

Comenzando con cualquier línea$\ell$ y punto A no encendido$l$, deja$m *$ ser el límite paralelo en$A$ a$l$, dejar$M$ ser el pie de la perpendicular de$A$ a $l$, y dejar$B$ ser el punto a lo largo del rayo AM con$\mathrm{MB} \cong \mathrm{MA}$. Ahora copie el ángulo crítico en el$\mathrm{A}$ lado opuesto de$m^{*}$ y tome$C$ a lo largo del rayo determinado con$A C A B$. Entonces$\Delta \mathrm{ABC}$ es un triángulo que no se puede circunscribir. ¿Por qué? [Ver$\mathrm{PS} 3, \# 16 .]$

En lugar de probar resultados más profundos de la geometría hiperbólica, los dos últimos capítulos estudiarán la geometría obtenida asumiendo el postulado paralelo más familiar en lugar del hiperbólico. Es decir, estudiaremos la geometría euclidiana con el objetivo principal de delinear una prueba de que el modelo de disco de Poincaré es realmente un modelo de geometría hiperbólica construido completamente dentro de la geometría euclidiana. Por implicación, si la geometría hiperbólica tuviera alguna inconsistencia inherente, podrían ser transportadas para exhibir inconsistencias dentro de la geometría euclidiana. En la lengua vernácula, la geometría hiperbólica es relativamente consistente con la geometría euclidiana. Es decir, si tiramos la geometría hiperbólica, tendríamos que rechazar también la geometría euclidiana. La mayoría de nosotros no queremos hacer eso.