3.2: Conjunto de problemas 3

A menos que se indique lo contrario, asuma todos los axiomas de geometría neutra (aunque no declarada) y también la forma global del Postulado Paralelo Hiperbólico (HPP); es decir, asumir geometría hiperbólica.

1. Demostrar que la suma de los ángulos interiores de cualquier triángulo es menor que dos ángulos rectos\(\left(180^{\circ}\right)\).
2. No asuma el HPP pero sí asuma que hay un triángulo para el cual la suma de los ángulos interiores es menor que\(180^{\circ}\). Demostrar la forma local del HPP.
3. No asuma el HPP pero sí asuma que hay un par de líneas paralelas que comparten una transversal que forma un par de ángulos interiores alternos no congruentes. Demostrar la forma local del HPP.
4. Demostrar que la cumbre de un cuadrilátero saccheri nunca es un límite (límite) paralelo a su base.
5. Demostrar que un lado de un cuadrilátero Lambert nunca es un límite (límite) paralelo a su lado opuesto.
6. Demostrar que dos líneas no comparten más de una perpendicular común (es decir, no hay “ataduras de vías férreas”).

En Exs 7-10, considere el modelo Poincaré de geometría hiperbólica en geometría euclidiana determinado por el círculo de radio 2 centrado en el origen\(\mathrm{O}(0,0)\) del plano cartesiano,\(\gamma=\left\{(\mathrm{x}, \mathrm{y}) \mid \mathrm{x}^{2}+\mathrm{y}^{2}<2^{2}\right\}\)

7. Encuentre la ecuación para el círculo\(\delta\) que determina el límite correcto (límite) paralelo al\(\mathrm{x}\) eje -en el punto\(\mathrm{P}(1,1)\) y esboce con precisión la situación.

[Pista: El centro de este círculo debe estar en la línea\(x=2\). ¿Por qué? Recordemos la ecuación del círculo con centro\(\mathrm{C}(\mathrm{h}, \mathrm{k})\) y radio\(\mathrm{r}: \delta=\left\{(\mathrm{x}, \mathrm{y}) \mid(\mathrm{x}-\mathrm{h})^{2}+(\mathrm{y}-\mathrm{k})^{2}=\mathrm{r}^{2}\right.\).]

9. Rehacer Ex 7 para el límite izquierdo paralelo en el mismo punto\(P(1,1)\).
10. Hacer un boceto preciso de la situación en los Exs 7 y 8 y “bosquejar” en la línea de Poincaré\(P(1,1)\) que es perpendicular al\(\mathrm{x}\) eje.
11. Encuentra la ecuación para el círculo euclidiano\(\delta\) de la línea Poincaré en el Ex 9. [Pista: Para la ortogonalidad con el\(\mathrm{x}\) eje -eje, su centro\(\mathrm{C}\) tendrá que estar en el\(\mathrm{x}\) -eje, digamos\((c, 0)\), así\((\mathrm{x}-\mathrm{c})^{2}+\mathrm{y}^{2}=\mathrm{r}^{2}\) es la ecuación y pasa a través de él\(\mathrm{P}(1,1)\). La condición adicional necesaria es la ortogonalidad con el círculo definitorio. Esto se puede hacer fácilmente usando el Teorema de Pitágoras con los radios y la distancia entre los centros,\(|c|\)
12. Considere el modelo Poincaré de geometría hiperbólica en geometría euclidiana determinado por el círculo de radio 4 centrado en el origen\(\mathrm{O}(0,0)\) del plano cartesiano,\(\gamma=\left\{(\mathrm{x}, \mathrm{y}) \mid \mathrm{x}^{2}+\mathrm{y}^{2}<4^{2}\right\}\). Encuentra la ecuación para el círculo euclidiano\(\delta\) de la línea Poincaré determinada por los puntos\(\mathrm{A}(1,2)\) y\(\mathrm{B}(3,0)\).

[Pista: Para su ecuación,\(\delta=\left\{(\mathrm{x}, \mathrm{y}) \mid(\mathrm{x}-\mathrm{h})^{2}+(\mathrm{y}-\mathrm{k})^{2}=\mathrm{r}^{2}\right.\), la ortogonalidad con el círculo definitorio puede estar involucrada usando el teorema de Pitágoras:\(4^{2}+r^{2}=h^{2}+k^{2}\) así que\(r^{2}=h^{2}+k^{2}-4^{2}\). La bisectriz perpendicular del segmento euclidiano AB tiene pendiente 1, pasa por el punto medio\(\mathrm{M}(2,1)\), y (h, k).] 12. La idea del Ex 11 puede generalizarse para proporcionar una prueba analítica (Ver Chapt. 4) del Axioma 1 como teorema de geometría euclidiana como un paso en la prueba de que el modelo de Poincaré es realmente un modelo para geometría hiperbólica completamente dentro de la geometría euclidiana (estableciendo “consistencia relativa” de la geometría hiperbólica axiomas (ver Capítulo 5 para una prueba sintética trivial!). Consideremos el modelo Poincaré determinado por el círculo de radio\(\mathrm{R}\) centrado en el origen\(\mathrm{O}(0,0)\) del plano cartesiano,\(\gamma=\left\{(\mathrm{x}, \mathrm{y}) \mid \mathrm{x}^{2}+\mathrm{y}^{2}<\mathrm{R}^{2}\right\}\).

Encuentra la ecuación para el círculo euclidiano\(\delta\) de la línea Poincaré determinada por dos puntos generales de Poincaré\(\mathrm{A}\left(\mathrm{a}_{\mathrm{x}}, \mathrm{a}_{\mathrm{y}}\right)\) y\(\mathrm{B}\left(\mathrm{b}_{\mathrm{x}}, \mathrm{b}_{\mathrm{y}}\right)\) dónde\(\mathrm{A}, \mathrm{B}\), y no\(\mathrm{O}\) son colineales.

Es decir, si\((\mathrm{x}-\mathrm{h})^{2}+(\mathrm{y}-\mathrm{k})^{2}=\mathrm{r}^{2}\) es su ecuación, express\(\mathrm{h}, \mathrm{k}\), y r únicamente en términos de\(\mathrm{R}\) y las coordenadas de\(A\) y B. La ortogonalidad con el círculo definitorio puede estar involucrada usando el teorema de Pitágoras:

\(\mathrm{R}^{2}+\mathrm{r}^{2}=\mathrm{h}^{2}+\mathrm{k}^{2}\)para que\(\mathrm{r}^{2}=\mathrm{h}^{2}+\mathrm{k}^{2}-\mathrm{R}^{2}\). La bisectriz perpendicular del segmento euclidiano AB tiene que pasar por su punto medio\(\mathrm{M}\) y el centro del círculo\(\mathrm{C}(\mathrm{h}, \mathrm{k})\). Se presentan tres casos siendo el más general que la línea euclidiana no\(A B\) es ni vertical ni horizontal. En ese caso, calcular la ecuación de la bisectriz perpendicular,\(\mathrm{y}=\mathrm{mx}+\mathrm{b}\)\(\mathrm{m}\) siendo el recíproco negativo de la pendiente de la línea AB y utilizando\(M\) para calcular b. ya que\(C\) está en esa línea, tenemos\(k=m h+b\) y, sustituyendo en las coordenadas de cualquiera de A o\(\mathrm{B}\) que deben estar en el círculo, tendremos\((\mathrm{x}-\mathrm{h})^{2}+(\mathrm{y}-\mathrm{k})^{2}=\mathrm{r}^{2}=\mathrm{h}^{2}+\mathrm{k}^{2}-\mathrm{R}^{2}\) enteramente en términos de\(\mathrm{h}(\) y los coeficientes dados). Por suerte, los términos que implican\(h^{2}\) cancelan y podemos resolver de manera única para h, entonces\(\mathrm{k}=\mathrm{mh}+\mathrm{b}\), y finalmente\(\mathrm{r}^{2}=\mathrm{h}^{2}+\mathrm{k}^{2}-\mathrm{R}^{2}\). Es decir, hay uno y sólo uno de esos círculos. Los otros dos casos usan la misma idea pero son más fáciles.

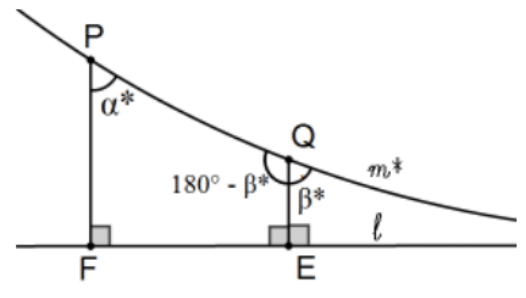
13. Demostrar que los ángulos de paralelismo aumentan estrictamente a lo largo de los paralelos fronterizos en la dirección de la amplitud.

[Pista: La cifra dada lo dice todo:\(\alpha^{*}+\left(180-\beta^{*}\right)<180^{\circ}\) porque PQEF es un cuadrilátero.]

Un polígono puede ser circunscrito si hay un círculo, llamado circuncírculo, que contiene cada vértice del polígono. Debe ser obvio que un polígono puede ser circunscrito si hay un punto equidistante de cada uno de sus vértices.

14. Demostrar que un cuadrilátero Lambert nunca puede ser circunscrito. [Pista: Supongamos que hay un círculo circunscrito y derivar una contradicción; es decir, usar prueba por contradicción. Nota: No asuma que la intersección de las diagonales es el centro del supuesto circumcircle pero puede usar el hecho de que tendría que tener un centro.]

15. Construir el circuncírculo de un cuadrilátero Saccheri. [Pista: Construye los bisectores perpendiculares de una pata y la base y prueba que la intersección es equidistante de cada uno de los vértices, de ahí el centro del circuncírculo.]
16. Completar la prueba de que los triángulos del último teorema del capítulo son triángulos genuinos y que no pueden ser circunscritos. [¿Por qué falla la presentación en geometría euclidiana?]
17. Demostrar por un cuidadoso boceto en el plano Poincaré que no todos los triángulos pueden ser circunscritos y argumentar por qué no se puede circunscribir. ¿Un argumento Poincaré? ¿Un argumento euclidiano?

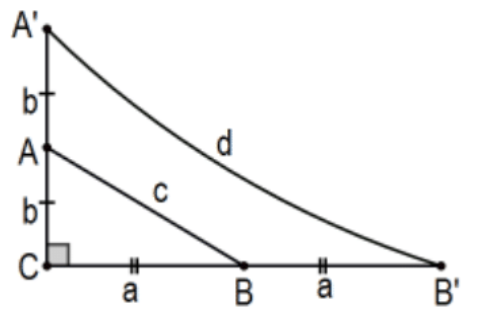
18. Demostrar que el Teorema de Pitágoras falla mostrando que si\(\triangle \mathrm{ABC}\) es un triángulo rectángulo con\(\mathrm{a}^{2}+\mathrm{b}^{2}=\mathrm{c}^{2}\), entonces un triángulo rectángulo con patas de 2a y\(2 \mathrm{~b}\) no satisface la ecuación pitagórica.

[Pista: Considere el cuadrilátero Saccheri asociado con la cumbre A\({ }^{\prime} \mathrm{B}^{\prime}\).]

19. Demostrar el Teorema de Cumbre.

20. Teorema: Si dos cuadriláteros saccheri tienen bases congruentes y cumbres congruentes, entonces son congruentes. [Es decir, demuéstralo.]

En Ex 21-24, supongamos que A y B son puntos dentro del círculo euclidiano fijo\(\gamma\) que define el modelo de disco de Poincaré para geometría hiperbólica,\(\delta\) es el círculo ortogonal determinado por A y\(\mathrm{B}\), y\(\mathrm{P}\) y\(\mathrm{Q}\) son los puntos de intersección de los círculos\(\gamma\) y\(\delta\). Recordemos que la distancia de Poincaré entre los puntos A y B (la medida del segmento de línea de Poincaré AB) es:

\[m_{p}(A B)=d_{p}(A, B)=|\ln (A, B ; P, Q)|=\left |\ln \left(\frac{A P / P B}{A Q / Q B} \right) \right|= \left| \ln \left(\frac{(A P)(Q B)}{(A Q)(P B)}\right) \right|. \nonumber\]

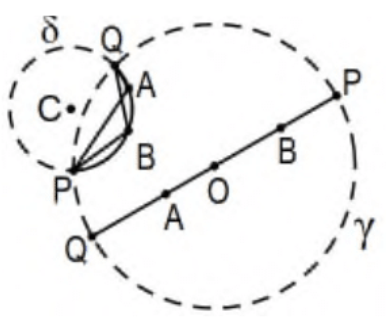
donde\(P\) y\(Q\) están determinados por la línea Poincaré determinada por\(A\) y\(B\).

21. Demostrar que la distancia Poincaré es independiente de qué punto está etiquetado como P y cuál es Q.

22. \(d_{p}(A, B)=d_{p}(B, A)\)Demuéstralo.
23. Demostrar que\(d_{p}(A, B)=0\) iff\(A=B\).
24. Demostrar que si\(A, B\), y\(C\) son puntos colineales en el modelo Poincaré,\(d_{p}(A, B)+d_{p}(B, C)=d_{p}(A, C)\) iff\(\mathrm{B}\) está entre A y C; es decir, entre ellos en la porción Poincaré del (mismo) círculo euclidiano determinado por dos cualesquiera de los puntos.

[Nota 1: No pasar por alto el detalle más importante, el hecho de que no necesariamente\(|\mathrm{x}|+|\mathrm{y}|\) es igual a\(|\mathrm{x}+\mathrm{y}|\) sólo "\(\geq\). Primero debes confirmar que, en cualquier situación que la uses, la igualdad se mantiene.]

[Nota 2: La noción completa de “entremedias” requiere que, para que B esté entre A y C, esta ecuación se mantenga sin la suposición de que los puntos sean colineales. Esto es cierto para las medidas Poincaré de segmentos de línea pero la prueba es mucho más difícil. Véase Capítulo 5, concluyendo con PS 5, #8.]

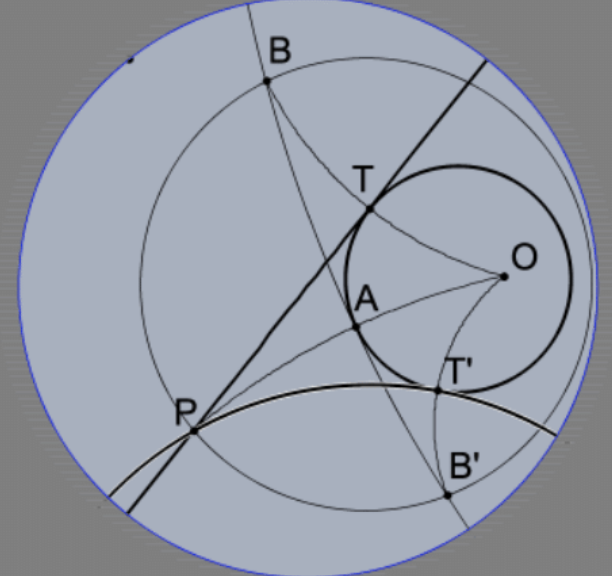
25. Suponiendo que el modelo de disco de Poincaré realmente es un modelo para geometría hiperbólica, recordar la construcción para las tangentes desde un punto P fuera del círculo O dado en PS 2, #28, y explicar la construcción indicada de líneas tangentes\(\mathrm{PT}\) y\(\mathrm{PT}^{\prime}\) al círculo de Poincaré (O; OA ) (es decir, centro\(\mathrm{O}\) de radio OA) en el modelo de disco Poincaré representado (suponiendo una “brújula Poincaré” y “recta Poincaré”) y demostrar que la construcción es válida. [Nota1: Eventualmente, incluiremos una construcción de las tangentes Poincaré usando las “herramientas euclidianas” (¡mucho más fáciles de conseguir!) pero eso es mucho más difícil. Nota 2: Los pasos de la construcción más conocida de estas tangentes en geometría euclidiana se pueden llevar a cabo con una brújula Poincaré y una recta en el modelo de disco Poincaré pero el resultado no es correcto. En otras palabras, ¡las pruebas importan!]

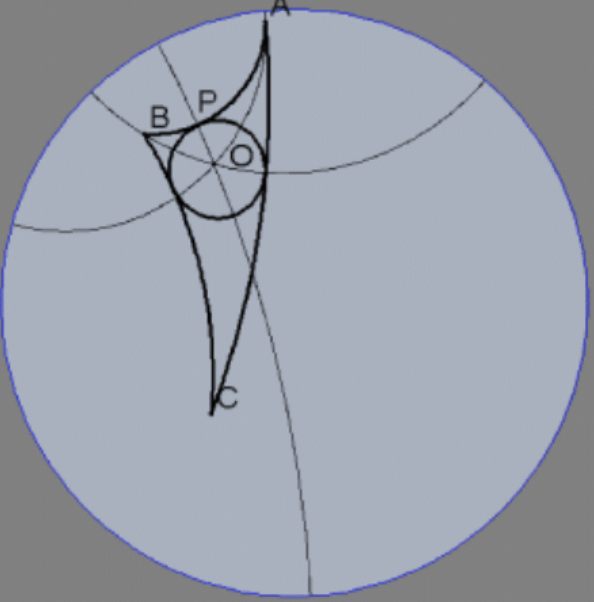
26. Suponiendo que el modelo de disco de Poincaré realmente es un modelo para geometría hiperbólica, recuerde la construcción para el círculo de un triángulo del Capítulo 2 (geometría neutra). Explique la construcción indicada del incircle del triángulo dado en el modelo de disco Poincaré ilustrado y demuestre que es válido.

[Nota: Al igual que con el Ej. 25, la construcción de la foto utiliza una brújula Poincaré y una recta pero es posible construir el círculo de un triángulo Poincaré con brújula euclidiana y una recta pero es sumamente tedioso.]

27a. El segmento\(\mathrm{A}_{1} \mathrm{~B}_{1}=[0,1]=\{\mathrm{x} \in \mathbf{R} \mid 0 \leq \mathrm{x} \leq 1\}\) tiene medida euclidiana 1 (sorpresa, sorpresa). Confirmar que su medida Poincaré está\(\ln (3)\) en el modelo Poincaré determinado\(\gamma=(\mathrm{O} ; 2)\) al explicar este cómputo:

\(\mathrm{m}_{f}([0,1])=\left|\ln \left(\frac{\mathrm{AP} / \mathrm{PB}}{\mathrm{AQ} / \mathrm{QB}}\right)\right|=\left|\ln \left(\frac{2 / 1}{2 / 3}\right)\right|=\left|\ln \left(\frac{3}{1}\right)\right|=|\ln (3)|=\ln (3)\)

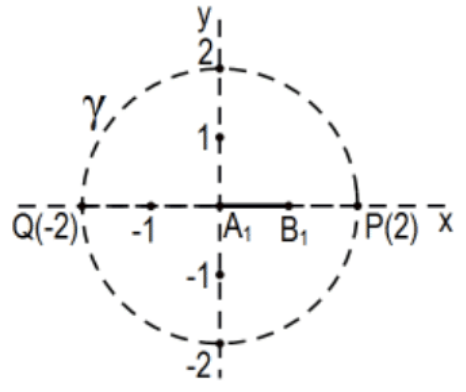
27b. Haga lo mismo para el segmento\(\mathrm{A}_{2} \mathrm{~B}_{2}=[1,3 / 2]\); es decir, calcule tanto sus medidas euclideanas como de Poincaré.

27c. Haz lo mismo para el segmento\(\mathrm{A}_{3} \mathrm{~B}_{3}=[3 / 2,7 / 4]\).

27d. Haz lo mismo para el segmento\(A_{n} B_{n}=\left[\left(2^{n-1}-1\right) / 2^{n-2},\left(2^{n}-1\right) / 2^{n-1}\right]\).

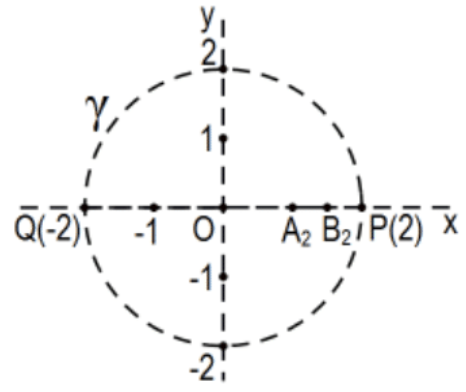
¿Cuál es el límite como\(n \rightarrow \infty\)?

Nota: Los segmentos del tipo\([0,1]\) en #27a anterior son especialmente fáciles de calcular:

Dejar\([0, x]\) ser el segmento euclidiano a lo largo del\(x\) -eje que es también un segmento en el modelo Poincaré definido por círculo\(\gamma=(\mathrm{O} ; \mathrm{R})\), segmento AB en la figura,\(0<\mathrm{x}<\mathrm{R}\). Claramente, su medida euclidiana es justa\(\mathrm{x}\). Por su medida Poincaré: [Aquí tomamos en cuenta la dirección así como la longitud euclidiana positiva.]

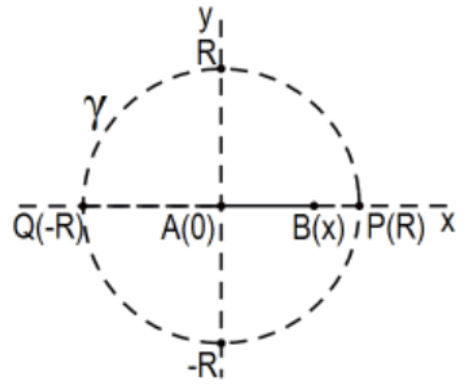
\[\mathrm{m}_{f}([0, \mathrm{x}])=\left|\ln \left(\frac{\mathrm{AP} / \mathrm{PB}}{\mathrm{AQ} / \mathrm{QB}}\right)\right|=\left|\ln \left(\frac{\mathrm{R} /(\mathrm{x}-\mathrm{R})}{-\mathrm{R} /(\mathrm{R}+\mathrm{x})}\right)\right|=\left|\ln \left(\frac{\mathrm{R}+\mathrm{x}}{\mathrm{R}-\mathrm{x}}\right)\right|=\ln \left(\frac{\mathrm{R}+\mathrm{x}}{\mathrm{R}-\mathrm{x}}\right) \nonumber\]

Note: The last expression makes it clear that, as \(\mathrm{x}\) approaches \(\mathrm{R}\), the length of segment [A(0), \(\mathrm{B}(\mathrm{x})]\) becomes infinite (as it must). In Chapter 5 (PS 5, #5), we will see that by an easy isometric (congruence) transformation, the Poincaré measure of any Poincaré segment in a Poincaré model in the \(\mathrm{x}\),y-coordinate (Cartesian) plane can be computed in this convenient manner, no simultaneous solution of two quadratic equations in two variables (to find the coordinates of the defining points \(P\) and \(Q\), and no Euclidean distance formula computations required.