5.1: Geometría euclidiana avanzada

Definición: Inversión de un Punto

La inversión de un punto$P \neq O$ en un círculo$\gamma$ con centro$\mathrm{O}$ y radio$\mathrm{R}$ es el punto$\mathrm{P}^{\prime}$ sobre rayo$\mathrm{OP}$ tal que$(\mathrm{OP})\left(\mathrm{OP}^{\prime}\right)=\mathrm{R}^{2}$.

Nota: A veces sólo estamos pensando en la inversión del punto P particular y en otras ocasiones estaremos pensando en la inversión de todo el “plano perforado”. ¿Por qué pinchado?

Ejemplo$\PageIndex{1}$

Construir la inversión de un punto dado$P \neq O$ en un círculo dado$\gamma$.

• Caso 1: P dentro del círculo.
• Caso 2: P en el círculo.
• Caso 3: P fuera del círculo.

Solución

Para el Caso 1, deje$\mathrm{T}$ ser (cualquiera de los dos puntos) determinado por la perpendicular al rayo$\mathrm{OP}$ en$\mathrm{P}$. Entonces$\mathrm{P}^{\prime}$ es la intersección del rayo$\mathrm{OP}$ con la tangente en$\mathrm{T}$, la perpendicular al radio a$\mathrm{T}$.

Dado que la línea$\mathrm{TP}$ es la altitud desde el ángulo recto del triángulo recto$\Delta \mathrm{OP}^{\prime} \mathrm{T}, \Delta \mathrm{TOP} \sim \Delta \mathrm{OP}^{\prime} \mathrm{T}$ así$\mathrm{OP} / \mathrm{OT}=\mathrm{OT} / \mathrm{OP}^{\prime}$ o$\mathrm{OP} / \mathrm{R}=\mathrm{R} / \mathrm{OP}^{\prime}$ y$(\mathrm{OP})\left(\mathrm{OP}^{\prime}\right)=\mathrm{R}^{2}$ como se desee.

Para el Caso 2,$\mathrm{P}=\mathrm{P}^{\prime}$ por lo que las instrucciones de construcción son “no hacer nada”!

Para el Caso 3, dejar$T_{1}$ y$T_{2}$ ser los puntos que determinan las líneas tangentes a partir de$P$. Entonces$P^{\prime}$ es la intersección del rayo$O P$ con la línea$T_{1} T_{2}$. (¿Por qué esta línea es perpendicular a la línea$\mathrm{OP}^{\prime}$?) La prueba es exactamente la del Caso 1 fue th con los roles de$\mathrm{P}$ e$\mathrm{P}^{\prime}$ intercambiado. QED.

Teorema fundamental de los círculos ortogonales

Si dos círculos$\gamma$ y se$\delta$ cruzan en puntos$\mathrm{A}$ y$\mathrm{B}$ con uno de los círculos centrados en$\mathrm{O}$$\mathrm{P}$ y y$\mathrm{Q}$ son puntos del otro círculo determinados por un rayo que se origina en$O$, entonces los círculos son ortogonales si$P$ y solo si y$Q$ son inversiones entre sí en el círculo$\gamma$ centrado en$O$.

Prueba: Considera Ray OA. Si los círculos son ortogonales, entonces el caso tangente del teorema secante establece la conclusión; es decir,$\mathrm{OP}(\mathrm{OQ})=(\mathrm{OA})^{2}=\mathrm{R}^{2}$.

Por el contrario, asumir$P$ y$Q$ son inversiones en círculo$\gamma$; es decir,$\mathrm{OP}(\mathrm{OQ})=(\mathrm{OA})^{2}=\mathrm{R}^{2}$. Si los círculos no fueran ortogonales, el rayo$\mathrm{OA}$ cruza el círculo en un segundo punto, digamos D, y habría un pedacito de$\mathrm{AD}=\mathrm{x}$ acorde,$\mathrm{OA}=\mathrm{R}$ siendo o bien el segmento interno de la secante de longitud$R+x$ (como se muestra en la imagen primero) o toda la secante con el segmento externo de longitud$R-x$ (segunda imagen). De cualquier manera, la hipótesis obliga$x$ a ser 0 y$\mathrm{OA}$ es una tangente de$\mathrm{O}$. De manera más explícita, tenemos$R(R \pm x)=R^{2}$. Es decir,$R \pm x=R$ para eso$x=0$ y tenemos ortogonalidad.

Corolario: Si un punto en un círculo (pensar P on$\delta$) está en el interior de otro círculo (pensar$\gamma$), los círculos son ortogonales si y solo si el centro del primer círculo se encuentra en la bisectriz perpendicular del segmento que une el punto con su inversión en el segundo círculo.

Teorema: Axioma 1 para el modelo Poincaré.

Prueba: Dejar$\gamma$ ser el círculo definitorio y dejar que A y B sean puntos distintos del plano no colineales con$O$. Entonces$\mathrm{A}^{\prime}$ y también$\mathrm{B}^{\prime}$ están en el círculo euclidiano deseado. Eso hace cuatro puntos no colineales, A, B, A', y$\mathrm{B}^{\prime}$, cualquiera de los cuales tres determinan completamente el círculo euclidiano único que determina el arco abierto que es la línea única de Poincaré deseada. Además, la construcción estándar para ese círculo es una construcción euclidiana de la línea Poincaré. Es decir, lo siguiente es una trivialidad:

Corolario: Construir la línea Poincaré determinada por dos puntos.

Más allá de eso, estos dos puntos euclidianos adicionales son muy útiles en el “globo ocular” esbozando la línea Poincaré determinada por los dos puntos, la línea en un punto perpendicular a una línea, el límite es paralelo a una línea en un punto, etc. No construya formalmente estos puntos (aunque algunos de estos ahora son fáciles construcciones euclidianas formales también; ver Juego de problemas 5) pero, si es necesario, usa una recta (borde de un libro, pedazo de papel doble, o algo así) y su conocimiento de círculos ortogonales para bosquejar la línea o líneas de Poincaré requeridas para el problema en consideración.

[Nota: Este es el Paso 1 de una prueba muy complicada, que todos los axiomas de geometría hiperbólica (señalados aquí o no) pueden probarse como teoremas de la geometría euclidiana sobre el modelo Poincaré a partir del cual podemos concluir que la geometría de Poincaré es relativamente consistente con Euclidiana geometría.]

Teorema: En la inversión de todo el plano perforado en un círculo fijo, los círculos y las líneas se mapean a líneas y círculos. Más explícitamente dejar$\gamma$ ser el círculo fijo con centro en$\mathrm{O}$ y radio de longitud$\mathrm{R}$. Entonces para cualquier figura euclidiana$\varphi$ que no contenga$\mathrm{O}$, vamos a$\varphi^{\prime}$ indicar la inversión de todos sus puntos en$\gamma$ y, si$\varphi$ contiene$\mathrm{O}$, deja$\varphi^{*}$ ser la misma figura euclidiana pero excluyendo$\mathrm{O}$, y dejar$\delta$ ser cualquier círculo y$\ell$ ser cualquier línea en el plano euclidiano. Entonces:

i. Si$O \in \delta$, entonces la inversión de$\delta^{*}$ es$\ell$, la línea perpendicular al rayo$O C$ en$\mathrm{D}^{\prime}$ donde$C$ está el centro de$\delta$ y$\mathrm{D}$ está determinada por el diámetro de$\delta$ determinado por el rayo OC.

ii. Si$\mathrm{O} \notin \ell$, entonces la inversión de$\ell$ es el círculo “perforado”$\delta^{*}$ donde$\mathrm{F}$ está el pie de la /perpendicular de$\mathrm{O}$ a$\ell$ y$\mathrm{OF}^{\prime}$ es el diámetro de $\delta$(es decir, la inversión de la inversión en i).

iii. Si$\mathrm{O} \in \ell$, entonces la inversión de$\ell^{*}$ es$\ell^{*}$ (la línea perforada giró de adentro hacia afuera).

iv. Si$\mathrm{O} \oplus \delta$, deje$\mathrm{C}$ ser su centro y segmento$\mathrm{AB}$ sea su diámetro determinado por la línea OC. Entonces la inversión de$\delta$ es el círculo$\delta^{\prime}$ con diámetro colineal$\mathrm{A}^{\prime} \mathrm{B}^{\prime}$ con dos casos a considerar:

a. Si$\mathrm{O} \oplus \mathrm{AB}$, entonces$\mathrm{A}^{\prime} \mathrm{B}^{\prime}$ es un subconjunto de rayo$\mathrm{AB}$ (el caso en la foto), o

b. Si$O \in A B$, entonces$O \in A^{\prime} B^{\prime}$ (porque$A$ y$A^{\prime}$ están en un lado de$O$ y$B$ y$B^{\prime}$ están en el otro).

Nos interesan especialmente las reflexiones del plano Poincaré en una línea Poincaré pero el teorema habla del plano euclidiano completo. Las reflexiones en una línea y las rotaciones alrededor de cualquier punto son demostrables como congruencias en geometría neutra, de ahí en geometría hiperbólica. El problema es que aún no sabemos que el modelo de disco de Poincaré incluso es un modelo para geometría hiperbólica; ¡asumir que tal sería asumir lo que estamos tratando de probar! (Los casos especiales de una reflexión a través de un diámetro y una rotación alrededor del centro son obvios pero no los otros).

Estas pruebas son fáciles pero requieren un poco de conocimiento,

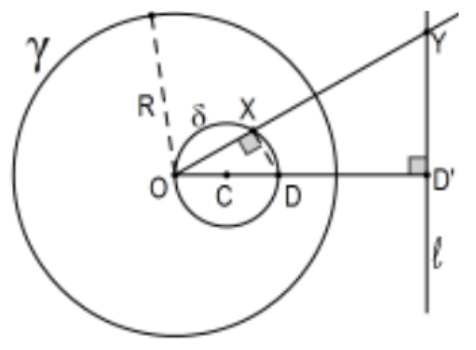
Caso$\mathrm{i}$: Dejar$\mathrm{X} \in \delta^{*}$ y dejar$\mathrm{Y}=\mathrm{f}(\mathrm{X})$ ser la intersección del rayo$\mathrm{OX}$ con$\ell$, la línea perpendicular al rayo$\mathrm{OC}^{\prime}$ en$\mathrm{D}^{\prime}$. Por AA Similaridad,$\triangle \mathrm{OD}^{\prime} \mathrm{Y}$ es similar a$\triangle \mathrm{OXD}$ pero así es$\Delta \mathrm{OD}^{\prime} \mathrm{X}^{\prime}$ así que$\mathrm{Y}=\mathrm{X}^{\prime}$ y tenemos$\ell=\delta^{* \prime}$ como reclamamos.

Caso ii: Esta es exactamente la misma idea solo que esta vez empezamos con F, el pie de la perpendicular de$\mathrm{O}$ a$l$ y dejó$\mathrm{F}^{\prime}$ ser su inversión en$\gamma$. Dejar$M$ ser el punto medio del segmento$\mathrm{OF}^{\prime}$. Dejar círculo$\delta^{*}=(\mathrm{M} ; \mathrm{MO})$; es decir, el círculo con centro en$\mathrm{M}$ de radio$\mathrm{MO}=\mathrm{MF}^{\prime}$. $\mathrm{X} \in \ell$Dejar$\mathrm{Y}=\mathrm{f}(\mathrm{X})$ ser el punto de intersección del rayo$\mathrm{OX}$ con$\delta *$. Ya que$\mathrm{OF}^{\prime}$ es un diámetro,$\triangle \mathrm{OYF}$ es un triángulo rectángulo así, por similitud AA,$\triangle \mathrm{OYF}{ }^{\prime} \sim \triangle \mathrm{OFX}$. Como antes,$\mathrm{Y}$ es la inversión de X; es decir,$\mathrm{Y}=\mathrm{X}^{\prime}$ y tenemos$l^{\prime}=\delta *$ como reclamamos.

Caso iii: Si lo piensas, es obvio.

$\underline{\text { Case iv a: }}$La construcción es fácil; la figura casi lo dice todo. Para círculo$\delta$, dejar$\mathrm{A}$ y$\mathrm{B}$ ser determinado por línea$\mathrm{OC}$, la línea de centros de los dos círculos$\mathrm{A}^{\prime}$ y y$\mathrm{B}^{\prime}$ ser sus inversiones con$M$ el punto medio de segmento $B^{\prime} A^{\prime}$. Después$\delta^{\prime}=\theta$, el círculo$\left(\mathrm{M} ; \mathrm{MA}{ }^{\prime}\right)$, con centro en$M$ y radio$\mathrm{MA}^{\prime}$. La parte complicada de la prueba es que la idea es que la inversión de$\delta$ es una dilatación (contracción) de sí misma desde O pero sólo como un conjunto, no “punto sabio”. Es decir, existe alguna constante$k$ tal que cada punto de$\delta^{\prime}$ está determinado por un punto de$\delta$ sobre el rayo desde el que determina$\mathrm{O}$ y$\mathrm{k}$ multiplican su distancia$\mathrm{O}$ (dilatación para$\mathrm{k}>1$, contracción para$0<\mathrm{k}<1$). Las dilataciones preservan los círculos porque conservan las formas; la proporción de cualquier par de distancias es la misma porque todos los factores de$k$ cancelación. La parte complicada es que la imagen es “girada de adentro hacia afuera” en contraposición a una dilatación “puntual” del plano euclidiano donde cada punto X del plano sería mapeado al punto a$\mathrm{O}$ lo largo$\mathrm{k}(\mathrm{OX})$ del mismo rayo. Eso no es cierto bajo inversión sino que, como conjunto de puntos, cualquier círculo es llevado a otro círculo, una dilatación de sí mismo. Para cualquiera$\mathrm{X} \in \delta$, deja$\mathrm{Y}$ ser el otro punto determinado por el rayo$\mathrm{OX}$ (si es tangente,$\mathrm{Y}=\mathrm{X}$). Ahora: $$O^{\prime}=\frac{R^{2}}{O Y}=\left(\frac{O X}{O X}\right) \frac{R^{2}}{O Y}=\frac{R^{2}}{(O X)(O Y)}(O X)=\frac{R^{2}}{(O A)(O B)}(O X) \nonumber$$ Donde la primera igualdad es la definición de inversión y la última es el uso del Teorema Secante. Es decir, la constante que necesitábamos es$\mathrm{k}=\mathrm{R}^{2} /(\mathrm{OA})(\mathrm{OB})$. El punto es que esta es una constante; es decir, solo depende del tamaño del círculo y su distancia desde$\mathrm{O}$, no de la elección del punto en el círculo.

[Nota: Muchos libros toman la constante para estar$k=R^{2} /(O T)^{2}=(R / O T)^{2}$ donde$T$ está una de las tangentes al círculo$\delta$ desde el punto$\mathrm{O}$, el mismo número del caso tangente del teorema secante. El problema es que hace que el Caso iv b sea más un caso especial de lo que necesita ser.]

$\underline{\text { Case iv b: }}$Esto es lo mismo excepto que la igualdad final se sostiene por el Teorema del Acorde en lugar de por el Teorema de la Secante. Esto verifica el resultado (pero con un giro; ver PS 5, #10).

Lema: Para dos puntos A y B no ambos colineales con el centro$\mathrm{O}$ del círculo$\boldsymbol{\gamma}$, y$\mathrm{A}^{\prime}$ y$\mathrm{B}^{\prime}$ las inversiones de$\mathrm{A}$ y$\mathrm{B}$ en el círculo,$\Delta \mathrm{OA}^{\prime} \mathrm{B}^{\prime} \sim \triangle \mathrm{OBA}$; i.e. , los triángulos son similares pero la correspondencia (por lo que los otros dos ángulos correspondientes) se intercambia.

Prueba: Como$\angle O$ es en común, por SAS Similitud, solo necesitamos verificar la relación de sus dos lados. Dejando$R$ ser el radio del círculo: $$\frac{O^{\prime}}{\mathrm{OB}}=\frac{\mathrm{R}^{2} / \mathrm{OA}}{\mathrm{OB}}=\frac{\mathrm{R}^{2}}{(\mathrm{OA})(\mathrm{OB})}=\frac{\mathrm{OB}^{\prime}}{\mathrm{OA}} \quad \text { so } \quad \mathrm{A}^{\prime} \mathrm{B}^{\prime}=\frac{\mathrm{R}^{2}}{(\mathrm{OA})(\mathrm{OB})} \nonumber$$

Teorema: La inversión en círculo preserva la relación cruzada. Es decir, si$A, B, C$, y$D$ son cuatro puntos invertidos en un círculo, entonces$(\mathrm{A}, \mathrm{B} ; \mathrm{C}, \mathrm{D})=\left(\mathrm{A}^{\prime}, \mathrm{B}^{\prime} ; \mathrm{C}^{\prime}, \mathrm{D}^{\prime}\right)$

Prueba: Este hecho importante es simplemente una aplicación del lema aplicado a la relación definitoria de relación cruzada. Más explícitamente, suponiendo que el círculo esté centrado en$\mathrm{O}$, use el lema en cada fracción definitoria y simplifique. La fracción del numerador: $$A^{\prime} C^{\prime}=\left(\frac{R^{2}}{(O A)(O C)}\right) A C \text { and } C^{\prime} B^{\prime}=\left(\frac{R^{2}}{(O C)(O B)}\right) C B \text { so that } \frac{A^{\prime} C^{\prime}}{C^{\prime} B^{\prime}}=\left(\frac{O B}{O A}\right)\left(\frac{A C}{C B}\right) \nonumber$$ La fracción denominador $$\mathrm{A}^{\prime} \mathrm{D}^{\prime}=\left(\frac{\mathrm{R}^{2}}{(\mathrm{OA})(\mathrm{OD})}\right) \mathrm{AD} \text { and } \mathrm{D}^{\prime} \mathrm{B}^{\prime}=\left(\frac{\mathrm{R}^{2}}{(\mathrm{OD})(\mathrm{OB})}\right) \mathrm{DB} \text { so that } \frac{\mathrm{A}^{\prime} \mathrm{D}^{\prime}}{\mathrm{D}^{\prime} \mathrm{B}^{\prime}}=\left(\frac{\mathrm{OB}}{\mathrm{OA}}\right)\left(\frac{\mathrm{AD}}{\mathrm{DB}}\right) \nonumber$$ Estas tienen el mismo multiplicador (OB/OA) por lo que cancelan y se conserva la relación cruzada. QED.

Teorema: La inversión en círculo conserva los ángulos formados por intersecciones de círculos y líneas.

[Nota: Este “círculos y líneas” es en el sentido de las propias figuras - la inversión de un círculo puede ser una línea o viceversa.]

Prueba: Esta es una consecuencia trivial del análisis complejo elemental, una función analítica (por lo que cualquier transformación fraccionaria lineal) es conforme (por lo que conserva el ángulo) en cualquier punto donde tenga una derivada distinta de cero. Esto no es del todo inversión en un círculo pero, con la elección adecuada de los coeficientes y seguida de una reflexión en el$x$ eje -( conjugación), lo es. Este poder, por supuesto, no está disponible para nosotros en un entorno de geometría estrictamente euclidiana, así que aquí hay una prueba de geometría sintética.

Se deben considerar varios casos, un ángulo convencional: la unión de dos rayos (con un punto inicial común), el arco de un círculo y un rayo, y la unión de arcos de dos círculos. Además, la situación es diferente dependiendo de si el círculo de un rayo o la línea de un rayo de un ángulo contiene el centro del círculo de inversión; esta última situación es lo suficientemente conveniente como para obligarlo a simplificar las otras situaciones. Por ejemplo, consideremos un ángulo determinado por dos círculos que no contienen el centro del círculo de inversión; necesitamos demostrar que el ángulo entre sus círculos de inversión no cambia; es decir, el ángulo formado por sus tangentes en el punto de intersección es el mismo después de la inversión. Tenga en cuenta que estas son NUEVAS líneas tangentes, no inversiones entre sí -la inversión de una línea que no contiene el centro del círculo de inversión, ni siquiera es una línea- es un círculo que sí contiene el centro. $\angle A=\angle B A C$Para arcos$\mathrm{AB}$ y$\mathrm{AC}$. Tenemos que demostrar que los ángulos entre las tangentes a los círculos en$\mathrm{A}$ y$\mathrm{A}^{\prime}$ son congruentes; es decir, tenemos que probar que los ángulos convencionales$\angle \mathrm{SAV} \cong \angle \mathrm{UA}^{\prime} \mathrm{W}$ donde$\mathrm{S}, \mathrm{U}, \mathrm{V}$, y$\mathrm{W}$ son cualquier punto a lo largo de los rayos determinado por los rayos tangentes a los círculos en$\mathrm{A}$ y$\mathrm{A}^{\prime}$ como se indica.

Basta con “dividir el ángulo”$\angle \mathrm{A}=\angle \mathrm{BAC}$ por la línea$\mathrm{OA}=\mathrm{OA}$ '(que contiene ambos vértices de ángulo) de la siguiente manera: Dejando que D sea la otra intersección del rayo OA con el círculo de arco AB, podemos considerar el ángulo original como dos ángulos de la misma suma de medida$\alpha=\alpha_{1}+\alpha_{2}$ donde estas son las medidas de$\angle$ BA y$\angle \mathrm{DAC}$, respectivamente. El otro caso especial, pero manejado de manera similar, es para$\alpha=\alpha_{1}-\alpha_{2}$.

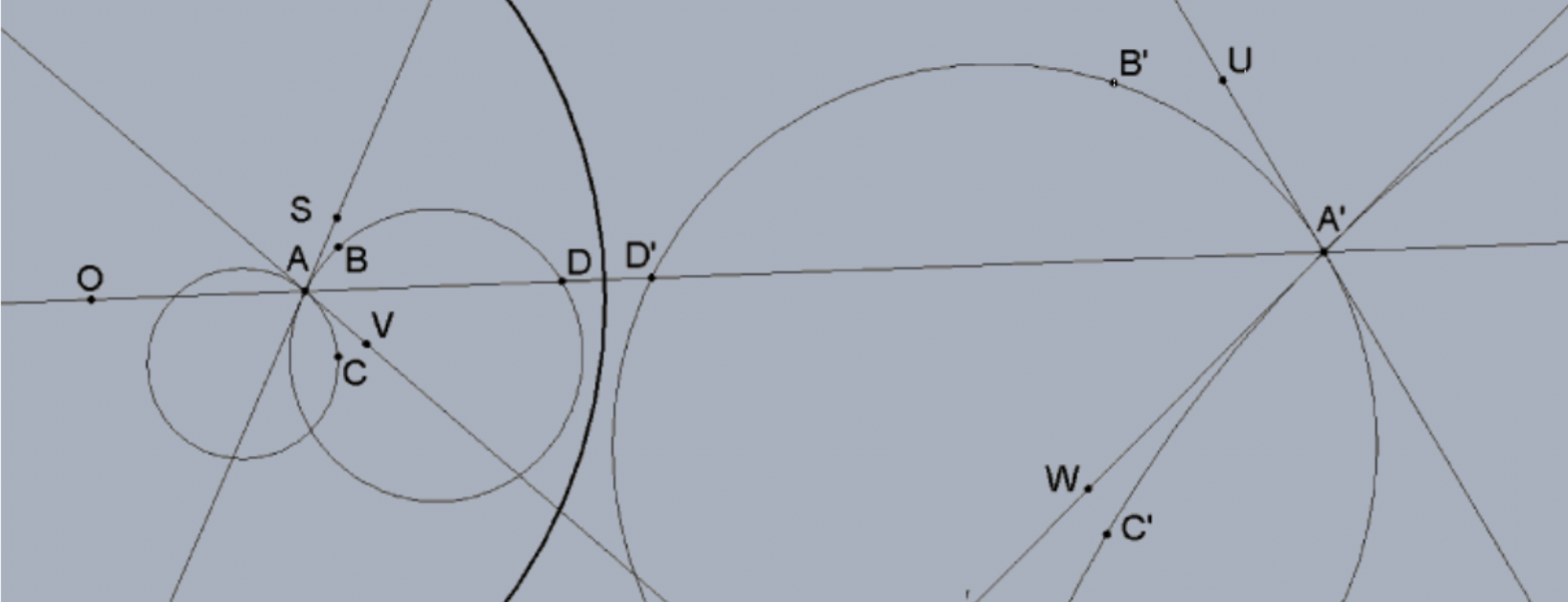
Es decir, y sin pérdida de generalidad, podemos suponer que uno de los rayos del ángulo en A está en la línea OA (así podemos ignorar la porción del ángulo debajo de la línea OA). Obsérvese que en este caso restringido, la inversión del rayo angular$\mathrm{AD}$ es el otro rayo angular$\mathrm{A}^{\prime} \mathrm{D}^{\prime}$ ya que la inversión de una línea (perforada) que contiene el centro del círculo de inversión es la misma línea “girada del revés”. Esta idea de suponer que un lado del ángulo está en la línea determinada por el centro de inversión y el vértice del ángulo$(\mathrm{O}$ y A, respectivamente) reduce en gran medida el número de casos necesarios para probar el teorema debido a que cada parte del ángulo dividido se puede considerar por separado y nosotros no tiene que preocuparse por ángulos con un lado contenido en una línea a través del centro de inversión (¡todos estos son de ese tipo!) :

Caso 1: Un arco de un círculo a un arco de un círculo (como se muestra a continuación).

Caso 2: Un arco de círculo que contiene el centro de inversión a un rayo.

Caso 3: Un rayo dentro de una línea que no contiene el centro de inversión a un arco de un círculo que sí.

Para ello, dejar$X$ y$Y$ ser las intersecciones diametrales del círculo de arco$A B$ determinadas por el centro de inversión$\mathrm{O}$ y el centro del círculo de arco$\mathrm{AB}$ con inversiones como se indica $\mathrm{X}^{\prime}$y$\mathrm{Y}^{\prime}$. Identificaremos estos círculos por estos diámetros$(X Y)$ y$\left(X^{\prime} Y^{\prime}\right)$. Por teorema anterior,$\Delta O D X \approx \Delta O X^{\prime} D^{\prime}$ así que$\angle \mathrm{ODX} \cong \angle \mathrm{OX}^{\prime} \mathrm{D}^{\prime}$. Por el teorema del ángulo inscrito (y el hecho$\angle \mathrm{ODX}=\angle \mathrm{ADX}$) de que$\mathrm{m}(\angle \mathrm{ADX})=(1 / 2)(\mathrm{AX})$ dónde$\mathrm{AX}$ está el arco subtendido de círculo$(\mathrm{XY})$ y$\mathrm{m}\left(\angle \mathrm{Y}^{\prime} \mathrm{X}^{\prime} \mathrm{D}^{\prime}\right)=(1 / 2)\left(\mathrm{Y}^{\prime} \mathrm{D}^{\prime}\right)$. $\angle \mathrm{OXD} \cong \angle \mathrm{OD}^{\prime} \mathrm{X}^{\prime}$Así mismo, por suplementación,$\angle \mathrm{DXY} \cong \angle \mathrm{X}^{\prime} \mathrm{D}^{\prime} \mathrm{A}^{\prime}$ y arco$\mathrm{DY}$ de círculo (XY) tiene la misma medida que arco$\mathrm{A}^{\prime} \mathrm{X}^{\prime}$ de círculo$\left(\mathrm{X}^{\prime} \mathrm{Y}^{\prime}\right)$. En cada círculo, los tres arcos forman un semcírculo:$\mathrm{XA}+\mathrm{AD}+\mathrm{DY}$ de círculo (XY) y$\mathrm{X}^{\prime} \mathrm{A}^{\prime}+\mathrm{A}^{\prime} \mathrm{D}^{\prime}+\mathrm{D}^{\prime} \mathrm{Y}^{\prime}$ de círculo$\left(\mathrm{X}^{\prime} \mathrm{Y}^{\prime}\right)$ con dos de los tres arcos siendo iguales en medida. Ya que juntos hacen semicírculos (180 si se usa medida de grado), concluimos que el arco AD de círculo (XY) tiene la misma medida que el arco$\mathrm{A}^{\prime} \mathrm{D}^{\prime}$ de círculo$\left(\mathrm{X}^{\prime} \mathrm{Y}^{\prime}\right)$. Por el caso tangente del teorema del ángulo inscrito,$\alpha_{1}=m(\angle S A D)=(1 / 2)(A D)=(1 / 2)\left(A^{\prime} D^{\prime}\right)=m\left(\angle U^{\prime} D^{\prime}\right)$.

Caso 2: Un arco de círculo que contiene el centro de inversión a un rayo.

En este caso, la inversión de$\angle B A D$ donde$A B$ es un arco de círculo que contiene$O$ es el ángulo genuino$\angle \mathrm{B}^{\prime} \mathrm{A}^{\prime} \mathrm{D}^{\prime}$. Por teorema anterior,$\triangle \mathrm{OBA} \approx \triangle \mathrm{OA}^{\prime} \mathrm{B}^{\prime}$ así que$\angle \mathrm{OAB} \cong \angle \mathrm{OB}^{\prime} \mathrm{A}^{\prime}$. Por el teorema del ángulo inscrito,$\mathrm{m}(\angle \mathrm{OAB})=(1 / 2)(\mathrm{OB})$ donde$\mathrm{OB}$ está el arco subtendido del círculo original. Además, el resto del arco$\mathrm{OA}$$\mathrm{BA}$, es subtendido por$\angle \mathrm{O}$ y todo el arco da la medida del ángulo tangente$\mathrm{m}(\angle \mathrm{SAD})=(1 / 2)(\mathrm{OA})$. Ahora considere triángulo$\Delta \mathrm{OA}^{\prime} \mathrm{B}^{\prime}$ y su ángulo externo en$\mathrm{A}^{\prime}$. Por la forma euclidiana del Teorema del Ángulo Exterior,$\angle \mathrm{B}^{\prime} \mathrm{A}^{\prime} \mathrm{D}^{\prime}$ es la suma de los dos ángulos interiores no adyacentes, el ángulo en$\mathrm{O}$ y$\angle \mathrm{OB}^{\prime} \mathrm{A}^{\prime} \cong \angle \mathrm{A}$. Es decir, el ángulo de inversión en$\mathrm{A}^{\prime}$ concuerda con el ángulo tangente$A$ según sea necesario.

$\underline{\text { Case 3: A ray within a line that does not contain the center of inversion to an arc of a circle that does. (This }$es el reverso del Caso 2 con pruebas muy similares.)

En este caso, la inversión del ángulo real$\angle B A D$ es$\angle B^{\prime} A^{\prime} D^{\prime}$ donde se encuentra$A^{\prime} B^{\prime}$ un arco de círculo, la inversión de línea$\mathrm{AB}$. Por teorema anterior, de$\triangle \mathrm{OBA} \approx \triangle \mathrm{OA}^{\prime} \mathrm{B}^{\prime}$ manera que$\angle \mathrm{OBA} \cong \angle \mathrm{OA}^{\prime} \mathrm{B}^{\prime}$, por el teorema del ángulo inscrito,$\mathrm{m}\left(\angle \mathrm{OA}^{\prime} \mathrm{B}^{\prime}\right)=(1 / 2)\left(\mathrm{OB}^{\prime}\right)$ donde$\mathrm{OB}^{\prime}$ está el arco subtendido del círculo de inversión. Además, el resto del arco$\mathrm{OA}^{\prime}$ es arco$\mathrm{B}^{\prime} \mathrm{A}^{\prime}$ que está subtendido$\angle \mathrm{O}$ y todo el arco da la medida del ángulo tangente$\mathrm{m}\left(\angle \mathrm{UA}^{\prime} \mathrm{D}^{\prime}\right)=(1 / 2)\left(\mathrm{OA}^{\prime}\right)$. Ahora considere el triángulo$\Delta \mathrm{OAB}$ y su ángulo externo en A. Por la forma euclidiana del Teorema del Ángulo Exterior, nuestro original$\angle \mathrm{BAD}$ es la suma de los dos ángulos interiores no adyacentes, exactamente el ángulo en$\mathrm{O}$ y$\angle \mathrm{OA}^{\prime} \mathrm{B}^{\prime} \cong \angle \mathrm{B}$. Es decir, el ángulo original en$\mathrm{A}$ concuerda con el ángulo tangente at$\mathrm{A}^{\prime}$.

¿La situación cambia si el rayo AD se invierte? Ligeramente, y digno de comentario, pero no mucho. El mismo argumento junto con la suplementación confirma el mismo resultado. QED.

Teorema: La reflexión en una línea Poincaré (es decir, inversión en su círculo euclidiano) es una congruencia del plano Poincaré.

Prueba: Hemos hecho algunas ondas a mano pero las piezas están todas en su lugar. Es decir, se conservan los ángulos y se conserva la distancia de Poincaré entre dos puntos (es decir, longitudes de segmentos de línea de Poincaré) (a nivel de relación cruzada). Todo lo que queda es ver por qué tal inversión lleva el disco definitorio de nuevo sobre sí mismo. Es obvio cuando se piensa en ello. De manera explícita, cada punto del “interior” del círculo definitorio se invierte a su punto correspondiente en el “exterior” y viceversa incluyendo los puntos límite del círculo definitorio a los puntos límite correspondientes y todos los puntos entre ellos se invierten de manera similar. QED.

Teorema: Dado cualquier punto del disco de Poincaré, existe una única línea euclidiana constructible de Poincaré (es decir, círculo euclidiano) tal que la reflexión en esa línea lleva el punto al centro del disco.

[Nota: Este es un caso especialmente fácil de construir la línea única de Poincaré de tal manera que la reflexión (Poincaré) en esa línea lleve cualquier punto dado a cualquier otro punto dado. General: PS 5, #16.]

Construcción: Si esto va a ser un modelo para geometría hiperbólica, que debe haber tal línea es consecuencia de la geometría neutra (aunque no la probamos) ya que la reflexión en la bisectriz perpendicular del segmento de línea que une dos puntos cualesquiera en geometría neutra es la línea única con esa propiedad. No obstante, aún no sabemos que se trata de un modelo por lo que ese hecho no está disponible para nosotros. Ese hecho sí, sin embargo, nos ayuda a saber cómo proceder. Sorprendentemente, si$A$ es el punto y$\mathrm{O}$ es el centro de$\gamma$, el círculo definitorio, la construcción estándar de su inversión en el círculo, ¡nos da todo! Esta vez, sin embargo, identificaremos la inversión de$A$ en este círculo por$A *$ con el fin de reservar$A^{\prime}$ para la inversión de$A$ en el nuevo círculo aún por ubicar.

Dejando$P$ ser la intersección de la perpendicular al rayo$\mathrm{A}$ en$A$ con$\gamma$, recordar que$A *$ está determinada por la perpendicular en$P$ al radio OP. Entonces el círculo$(A * ; A * P)=\delta$ determina la línea de Poincaré deseada, l. Haciendo hincapié en esta conclusión, el círculo necesario se centra en la inversión de A en el círculo definitorio con radio ya determinado en su construcción!

Prueba: Tenemos que probarlo$(A * A)(A * O)=(A * P)^{2}$ y que este círculo euclidiano determina una línea Poincaré. La ortogonalidad es una trivialidad (¡por construcción!) y, ya que$P A$ es la altitud desde el ángulo recto de$\Delta \mathrm{OA} * \mathrm{P}, \Delta \mathrm{OA} * \mathrm{P} \sim \Delta \mathrm{PA} * \mathrm{~A}$ desde el cual$(\mathrm{A} * \mathrm{O}) /(\mathrm{A} * \mathrm{P})=(\mathrm{A} * \mathrm{P}) /(\mathrm{A} * \mathrm{~A})$ o$(\mathrm{A} * \mathrm{~A})(\mathrm{A} * \mathrm{O})=(\mathrm{A} * \mathrm{P})^{2}$ así$\mathrm{O}$ es la inversión de$A$ en este círculo ortogonal centrada en$A^{*}$; es decir, es el reflejo de$A$ en esa línea Poincaré. ¿Por qué no hay otro círculo así? La inversión en círculo (reflexión en una línea Poincaré) preserva la relación cruzada de manera que el punto de intersección,$M$ en la figura, debe ser el punto medio Poincaré del segmento AO. Dado que el centro de cualquier círculo ortogonal que llevaría A a$\mathrm{O}$ debe estar sobre el rayo$\mathrm{OA}$ y la reflexión tendría que preservar M (es decir, no moverlo), este círculo tendría que ser perpendicular a la línea OA así como ortogonal al círculo definitorio obligándolo a ser la misma línea; es decir, singularidad. Tenga en cuenta que esto$l$ determina el punto medio$\mathrm{M}$ del segmento AO y es perpendicular a su línea por lo que es la bisectriz perpendicular del segmento AO.QED.

Lema: Un punto del modelo de disco de Poincaré está más cerca del centro del círculo definitorio que otro punto usando la medida euclidiana si y solo si está más cerca usando la medida de Poincaré.

Prueba: Dejar$\mathrm{X}$ y$\mathrm{Y}$ ser los puntos con$\mathrm{X}$ más cerca$\mathrm{O}$ que$\mathrm{Y}$ usando la medida euclidiana como se indica. Gire cada segmento y su diámetro para que los segmentos estén en la misma dirección a lo largo del mismo diámetro. Las longitudes de los segmentos, ya sean euclidianos o Poincaré, permanecen sin cambios pero ahora determinan las mismas intersecciones con el círculo definitorio y las medidas euclidianas de los segmentos$\mathrm{OX}$ y$\mathrm{OY}$ pueden verse como números reales en la línea numérica euclidiana: con $-\mathrm{R}<0<\mathrm{x}<\mathrm{y}<\mathrm{R}$.

Comparando sus relaciones cruzadas:

$(\mathrm{O}, \mathrm{X} ; \mathrm{R},-\mathrm{R})=(\mathrm{R} /(\mathrm{R}-\mathrm{x})) /(\mathrm{R} /(\mathrm{R}+\mathrm{x}))=(\mathrm{R}+\mathrm{x}) /(\mathrm{R}-\mathrm{x})$y de igual manera$(\mathrm{O}, \mathrm{Y} ; \mathrm{R},-\mathrm{R})=(\mathrm{R} /(\mathrm{R}-\mathrm{y})) /(\mathrm{R} /(\mathrm{R}+\mathrm{y}))=(\mathrm{R}+\mathrm{y}) /(\mathrm{R}-\mathrm{y})$

Aunque los numeradores y denominadores son todos positivos, la comparación de fracciones puede ser complicada:$\mathrm{R}+\mathrm{x}$ es mayor que$\mathrm{R}+\mathrm{y}$ pero también$\mathrm{R}-\mathrm{x}$ es mayor que R-y y un número mayor dividido por un número mayor puede ser menor.

Trabajando a la inversa de lo que buscamos:$(\mathrm{R}+\mathrm{x}) /(\mathrm{R}-\mathrm{x})<(\mathrm{R}+\mathrm{y}) /(\mathrm{R}-\mathrm{y})$ iff$(\mathrm{R}+\mathrm{x}) /(\mathrm{R}-\mathrm{y})<(\mathrm{R}+\mathrm{y}) /(\mathrm{R}-\mathrm{x})$ iff$R x-R y<R y-R x$ iff$2 R x<2 R y$ iff$x<y$. Ya que$x<y$, estas relaciones cruzadas satisfacen la misma desigualdad que las distancias de los puntos girados. Sin embargo, la relación cruzada no fue el punto, solo su longitud de Poincaré; es decir,$|\ln (\mathrm{O}, \mathrm{X} ; \mathrm{R},-\mathrm{R})|$ y$|\ln (\mathrm{O}, \mathrm{Y} ; \mathrm{R},-\mathrm{R})|$. Esto se desprende del hecho de que, por la alineación de los puntos, conocemos los valores:$\mathrm{R}-\mathrm{x}<\mathrm{R}+\mathrm{x}$ por lo que su cociente es mayor que 1 logaritmo tan positivo y de manera similar para$Y$. Dado que la función de logaritmo natural está aumentando estrictamente:

$|\ln (\mathrm{O}, \mathrm{X} ; \mathrm{R},-\mathrm{R})|=\ln (\mathrm{O}, \mathrm{X} ; \mathrm{R},-\mathrm{R})<\ln (\mathrm{O}, \mathrm{Y} ; \mathrm{R},-\mathrm{R})=|\ln (\mathrm{O}, \mathrm{Y} ; \mathrm{R},-\mathrm{R})|$. Es decir,$\mathrm{d}_{\mathrm{p}}(\mathrm{O}, \mathrm{X})<\mathrm{d}_{\mathrm{p}}(\mathrm{O}, \mathrm{Y})$. En lugar de lo contrario, es más fácil usar este resultado para probar lo inverso; en esencia, qué pasa si$x=y$ o si$x>y$. En caso$x=y$ de que el cálculo directo (trivial) lo confirme$d_{p}(O, X)=d_{p}(O, Y)$ y en el caso$x>y$, concluimos$d_{p}(O, X)>d_{p}(O, Y)$ intercambiando los roles de$x$ y$y$ en el anterior. QED.

Teorema: Los segmentos de línea de Poincaré son congruentes si y sólo si la reflexión de un punto final de cada uno de ellos hacia el centro del círculo definitorio (inversión en círculos ortogonales) son segmentos euclidianos congruentes.

Prueba: Esta es una consecuencia inmediata del Lema precedente y del hecho de que la inversión en un círculo ortogonal preserva la relación cruzada para que la reflexión en una línea de Poincaré conserve la medida Poincaré. Es decir, dos segmentos de Poincaré son congruentes si y sólo si sus imágenes reflejadas son segmentos de Poincaré congruentes y, dado que un punto final de cada segmento reflejado es el centro definitorio, también son segmentos euclidianos que son segmentos euclidianos congruentes si y solo si son segmentos congruentes de Poincaré. QED.

Teorema: Un círculo de Poincaré es (como conjunto) un círculo euclidiano que permanece completamente dentro del disco de Poincaré y su centro Poincaré es colineal con el centro del círculo definitorio y su centro euclidiano.

Pregunta: ¿No era esta la definición del círculo de Poincaré en el Capítulo 3? Sí, pero nosotros “engañamos”. En geometría neutra (en la que se subsume la geometría hiperbólica), el concepto “círculo” ya tiene una definición estándar por lo que este solo puede ser un modelo para geometría hiperbólica si la “definición” original es consistente con la definición real. Podemos probar ese hecho ahora que se ha desarrollado más sofisticación.

Prueba: Supongamos$C \in P$ y$r>0$. Por la definición (real) de círculo, el círculo Poincaré con centro$C$ y radio$r$ es$(C ; r)_{\mathrm{P}}=\left\{X \in P \mid d_{P}(C, X)=r\right\}$. Para probar que este conjunto es un círculo euclidiano, considera dos casos:

i.$C=O$, el centro del círculo definitorio, o

ii. $\mathrm{C} \neq \mathrm{O}$.

En el primer caso, los segmentos de Poincaré$\mathrm{OX}$ para todos también$\mathrm{X} \in \mathcal{P}$ son segmentos euclidianos y los segmentos de línea de$\mathrm{O}$ son congruentes como segmentos de Poincaré si y solo si son congruentes como segmentos euclidianos por el Lema precedente. Esto implica ese conjunto$(O ; r)_{P}=\left\{X \in P \mid d_{P}(O, X)=r\right\}=\left\{X \in P \mid d(O, X)=r_{E}\right\}$, la medida euclidiana del segmento para algún número real fijo$\mathrm{r}_{\mathrm{E}}$. Esta es exactamente la definición del círculo euclidiano$\left(\mathrm{O} ; \mathrm{r}_{\mathrm{E}}\right)$ para que el conjunto original de puntos,$(\mathrm{O} ; \mathrm{r})_{\mathrm{P}}$, sea un círculo euclidiano.

En el segundo caso, reflexionar$O$ en la línea única de Poincaré$\ell$ (inversión en el círculo ortogonal apropiado) que lleva de C a O. Desde la reflexión en$\ell$ conserva la distancia,$\left((C ; r)_{p}\right)^{\prime}=\left\{X^{\prime} \in P \mid d_{p}\left(C^{\prime}=O, X^{\prime}\right)=r\right\}$.

Dado que el$X^{\prime}$ de este conjunto contiene todos los elementos de$P$, este conjunto es exactamente$\left\{X \in P \mid d_{p}(O, X)=r\right\}$ y este conjunto es exactamente la definición del círculo Poincaré$(\mathrm{O} ; \mathrm{r})_{\mathrm{P}}$ que es, por caso$\mathrm{i}$, un círculo euclidiano. Reflejando$\ell$ una vez más, el conjunto invertido se invierte de nuevo sobre el conjunto original y, dado que la inversión de un círculo en un círculo es un círculo o una línea siendo imposible aquí una línea (el conjunto está contenido dentro del círculo definitorio por lo que no puede contener el centro de la ortogonal círculo de inversión) el conjunto original es un círculo euclidiano.

Por el contrario, supongamos que$\delta$ es un círculo euclidiano que está contenido en el interior de$($ que no está centrado en$O$, el centro del círculo definitorio. Construir su centro euclidiano$\mathrm{C}_{\mathrm{E}}$ por la construcción estándar y dejar$A$ y$\mathrm{B}$ ser los puntos de intersección del rayo$\mathrm{OC}_{\mathrm{E}}$ con$\delta$ para que el segmento$\mathrm{AB}$ sea un diámetro del círculo y también un segmento Poincaré ya que es colineal con$\mathrm{O}$. Elija un$3^{\text {rd }}$ punto$C \in \delta$ y construya la bisectriz perpendicular del segmento Poincaré$\mathrm{AC}$ (o$\mathrm{B}$ y$\mathrm{C}$) (consulte$\mathrm{PS} 5, \# 17$), identifique la intersección con AB como $\mathrm{C}_{\mathrm{P}}$que es Poincaré equidistante de$A$ y$C$ (o$B$ y y$C)$, y let$r=d_{p}\left(C_{p}, C\right)$. El reflejo euclidiano del plano en la línea será$\mathrm{OC}_{\mathrm{E}}=\mathrm{OC}_{\mathrm{P}}$ también un reflejo Poincaré en la misma línea (diámetro abierto euclidiano) identifica otro punto$\mathrm{D} \in \delta$ para el que también$\mathrm{C}_{\mathrm{P}}$ es Poincaré equidistante de A (por simetría de la situación con respecto a la línea de diámetro$\mathrm{OC}_{\mathrm{E}}$, ver$\mathrm{X}$ y$\mathrm{Y}$ en la prueba de #16). Ahora reflexiona$\rho$ en la línea única de Poincaré$l$ (inversión en el círculo ortogonal apropiado) que lleva$C_{p}$ a O. Ya que la reflexión en$l$ conserva distancia,$\mathrm{O}$ es la misma distancia Poincaré $r$de$\mathrm{A}^{\prime}, \mathrm{C}^{\prime}$, y$\mathrm{D}^{\prime}$ en$\delta^{\prime}$ adelante, la inversión de$\delta$, que debe ser un círculo euclidiano ya que es la inversión de un círculo euclidiano. Dado que$\mathrm{OA}^{\prime}, \mathrm{OC}^{\prime}$, y$\mathrm{OD}^{\prime}$ son segmentos$\mathrm{Poincaré}^{\prime}$ congruentes, también son segmentos congruentes euclidianos así$\mathrm{A}^{\prime}, \mathrm{C}^{\prime}$, y$\mathrm{D}^{\prime}$ son 3 puntos distintos en este círculo euclidiano que son equidistantes de$\mathrm{O}=\left(\mathrm{C}_{\mathrm{P}}\right)^{\prime}$ por lo que es el centro del círculo$\delta^{\prime}$. Reflexionando en$\ell$ una vez más, tenemos que no sólo$\delta=\delta^{\prime \prime}$ es un círculo euclidiano, es el círculo Poincaré$\left(C_{p} ; r\right)_{\mathrm{P}}$. QED.

Teorema: Las líneas de Poincaré son rectas.

Prueba: Esta afirmación irónica es un teorema importante y pretende señalar la naturaleza nebulosa de la “rectitud”. Nuestra experiencia es tan fuerte que pensamos que sabemos hasta que se nos pide describir lo que significa ser “heterosexual” en lenguaje matemáticamente defendible. En términos formales, no lo intentamos. En cambio, los subconjuntos que llamamos líneas tienen ciertas propiedades definitivas que nunca se discuten en cursos introductorios (¡a veces nunca!) e imponer un axioma (Axioma 1) que dos puntos determinan exactamente uno de esos conjuntos. La definición real de es cualquier subconjunto del conjunto de puntos (el plano) que separa el conjunto en tres subconjuntos convexos mutuamente disjuntos, el conjunto mismo y dos subconjuntos (ajustar análogamente para “planitud” de un plano en el espacio). Esto, por supuesto, presupone una noción de “convexo” que a su vez depende de la noción de entretiempo. Un conjunto es convexo si, para dos puntos cualesquiera del conjunto, el conjunto de todos los puntos entre ellos también está en el conjunto. En el lenguaje de la geometría, si hay dos puntos cualesquiera en el conjunto, también lo es el segmento de línea que determinan. Que una línea Poincaré, digamos$l$, sea convexa en sí misma es consecuencia de un resultado anterior,$\mathrm{PS} 3, \# 24$. La idea es que el concepto de distancia en geometría neutra debe satisfacer la forma estricta de la desigualdad triangular; es decir, para tres puntos distintos$A, B$, y$C$, punto$B$ está entre$A$ y$C$ iff $d_{p}(A, B)+d_{p}(B, C)=d_{p}(A, C)$. Ese ejercicio sólo verificó que la condición se cumple para tres puntos colineales en un modelo de disco de Poincaré. Cualquier 3 puntos (distintos) se hace a continuación.

Para t e otros dos conjuntos determinados por una línea Poincaré, demostramos el contrapositivo. Es decir, si el segmento de línea Poincaré se$A B$ cruza con una línea dada$l$ donde ni$A$ ni$B$ está adentro$l$ (como se muestra arriba), entonces los puntos están en lados opuestos de$l$. Para ello, en el siguiente modelo de disco de Poincaré, supongamos que$\mathrm{X}$ es la intersección de segmento$A B$ y línea$l$. La cifra parece implicar el resultado deseado pero que

hecho es consecuencia de la prueba; no es un hecho. $m$Sea la línea Poincaré en la que$\mathrm{X}$ se refleja sobre$\mathrm{O} ;$ i.e.,$\mathrm{O}=\mathrm{X}^{\prime}$ donde esta reflexión significa la inversión en el círculo de la cual$m$ es un arco que es ortogonal al círculo definitorio. Las líneas reflejadas$l^{\prime}$ y$\mathrm{A}^{\prime} \mathrm{B}^{\prime}$ son líneas euclidianas y el plano Poincaré se divide en subconjuntos de los dos medios planos del plano euclidiano determinados por la línea euclidiana de segmento$l^{\prime}$. Dado que también$A^{\prime} B^{\prime}$ es un segmento euclidiano con punto$O=X^{\prime}$ en el interior del segmento, la “rectitud” de las líneas euclidianas (es decir, convexidad de ambos medios planos) implica que$A$ 'y B' se encuentran en lados opuestos de la línea euclidiana $\ell^{\prime}$. Por propiedades de inversión en un círculo,$A$ y B debe estar en lados opuestos de$l$.

Hay otro tecnicismo que no debemos pasar por alto (¡junto con muchos otros que lo haremos!) : Necesitamos una función de distancia valorada real no negativa$\mathrm{d}$ en un conjunto$\mathrm{S}$ para satisfacer la propiedad de desigualdad triangular; para tres elementos cualesquiera$A, B$$C$, y, debe ser cierto que$d_{p}(A, B)+d_{p}(B, C) \geq d_{p}(A, C)$. Tenemos que verificar esta condición para conocer la distancia de Poincaré. Ya tenemos este resultado para puntos colineales pero necesitamos que sea cierto en general. Es tentador afirmar que, para los puntos no colineales, se trata de una consecuencia inmediata de la Proposición 20 de geometría neutra pero que es un razonamiento circular bastante complicado. Lo cierto es que al asumir geometría formal basada en medidas (es decir, aceptar Postulados de Regla y Transportador), esa proposición solo se probó aquí por razones históricas. El caso es que la desigualdad generalizada tenía que ser cierta axiomáticamente así que para ser un modelo válido se tiene que demostrar para el plano Poincaré (o cualquier otro modelo de un sistema axiomático de geometría neutra, hiperbólico o no).

Teorema: Para tres puntos no colineales$A, B$, y$C$ en un plano de disco de Poincaré,$\mathrm{d}_{\mathrm{p}}(\mathrm{A}, \mathrm{B})+\mathrm{d}_{\mathrm{p}}(\mathrm{B}, \mathrm{C})>\mathrm{d}_{\mathrm{p}}(\mathrm{A}, \mathrm{C})$

Prueba: Considera Poincaré$\triangle \mathrm{ABC}$. Por la siguiente razón, basta con probar únicamente el caso especial, que la hipotenusa de un triángulo rectángulo es mayor que cualquiera de sus patas. Por la construcción del Ex 10, podemos construir la perpendicular de B a línea$A C$, digamos$F$ para el pie de la perpendicular. Suponiendo que se ha probado el caso del triángulo rectángulo (la segunda figura),$d_{p}(A, B)>d_{p}(A, F)$ y de$d_{p}(B, C)>d_{p}(F, C)$ manera que$d_{p}(A, B)+d_{p}(B, C)>d_{p}(A, F)+d_{p}(F, C)=d_{p}(A, C)$ en el caso que$F$ cae entre$A$ y$C$ y$d_{p}(A, F)+d_{p}(F, C)>d_{p}(A, C)$ si $F$cae fuera del segmento Poincaré$\mathrm{AC}$

Para probar$\mathrm{d}_{\mathrm{p}}(\mathrm{A}, \mathrm{B})>\mathrm{d}_{\mathrm{p}}(\mathrm{A}, \mathrm{F})$ (y, por simetría$\left.\mathrm{d}_{\mathrm{p}}(\mathrm{B}, \mathrm{C})>\mathrm{d}_{\mathrm{p}}(\mathrm{F}, \mathrm{C})\right)$, (Poincaré) reflejar$A$$\mathrm{O}$ en$m$ (la tercera figura) la bisectriz perpendicular del segmento lineal de Poincaré$A O$ (es decir, inversión en el Circulo euclidiano). Esto determina Poincaré$\triangle \mathrm{OB}^{\prime} \mathrm{F}^{\prime} \cong \triangle \mathrm{ABF}$ así$\mathrm{AB} \cong \mathrm{OB}, \mathrm{AF} \cong \mathrm{OF}^{\prime}$, y$\angle \mathrm{OF}^{\prime} \mathrm{B}^{\prime} \cong \angle \mathrm{AFB}$ así que eso$\angle \mathrm{OF}^{\prime} \mathrm{B}^{\prime}$ es un ángulo recto. El resultado deseado se desprende de$\mathrm{PS} 5$, #8.

Teorema: SAS sostiene para el modelo Poincaré.

Prueba: Supongamos$\triangle \mathrm{ABC}$ y$\triangle \mathrm{XYZ}$ son triángulos Poincaré que satisfacen a SAS como triángulos Poincaré. Específicamente, supongamos que, con respecto a la medida de Poincaré$\mathrm{AB} \cong \mathrm{XY}, \mathrm{AC} \cong \mathrm{XZ}$,, y que sus ángulos incluidos sean congruentes,$\angle \mathrm{A} \cong \angle \mathrm{X}$. Reflejando$\mathrm{A}$$\mathrm{X}$ hacia$\mathrm{O}\left(\mathrm{A}^{\prime}\right)$ y hacia$\mathrm{O}\left(\mathrm{X}^{*}\right)$, las reflexiones en los bisectores perpendiculares (Poincaré) de segmentos$\mathrm{AO}$ y XO respectivamente; es decir, las líneas indicadas a través de sus puntos medios (Poincaré), $M$y$N$. Los reflejos de los triángulos conservan sus longitudes de Poincaré y medidas de ángulo para que$\triangle \mathrm{ABC} \cong \triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{C}^{\prime}$ y$\triangle \mathrm{XYZ} \cong \triangle \mathrm{X}^{*} \mathrm{Y}^{*} \mathrm{Z}^{*}\left(\right.$ con$\mathrm{O}=\mathrm{A}^{\prime}=\mathrm{X}^{*}$) así estos nuevos triángulos satisfagan las mismas condiciones de Poincaré que los originales; es decir,$\mathrm{OB}^{\prime} \cong \mathrm{OY}^{*}$ y $\mathrm{OC}^{\prime} \cong \mathrm{OZ}^{*}$(como segmentos de Poincaré) y sus ángulos incluidos también$\mathrm{O}$ son congruentes.

Por el teorema anterior, sin embargo, estos segmentos transformados (ya que son radios del círculo definitorio) también son congruentes como segmentos euclidianos por lo que los triángulos euclidianos que determinan son congruentes,$\triangle \mathrm{OB}^{\prime} \mathrm{C}^{\prime} \cong \triangle \mathrm{OY} * \mathrm{Z}^{*}$, por el$\mathrm{SAS}$ Axioma. Ahora bien un volteo (inversión) en un diámetro (como se muestra en la imagen) o una rotación alrededor$\mathrm{O}$ lleva un triángulo euclidiano$\Delta \mathrm{OB}^{\prime} \mathrm{C}^{\prime}$ sobre el otro,$\Delta \mathrm{OX}^{*} \mathrm{Y}^{*}$. Esta última inversión es una congruencia Poincaré así como euclidiana ya que las longitudes y ángulos Poincaré se conservan para los dos lados desde$\mathrm{O}$ y su ángulo incluido dejando solo su tercer lado (Poincaré) y otros dos ángulos. Estos deben coincidir también porque (por el Axioma 1) estos otros dos puntos determinan una línea única de Poincaré que determina el lado Poincaré en cuestión. Observaciones similares se aplican a los ángulos que estos arcos determinan con los dos lados radiales. Por simetría y transitividad (i.e., composición), los originales$\triangle \mathrm{ABC}$ y$\triangle \mathrm{XYZ}$ son congruentes como triángulos de Poincaré. QED.

Teorema: El modelo de Poincaré es un modelo para geometría hiperbólica.

Prueba: Primero tendríamos que precisar todo el resto de esos axiomas no especificados y luego probarlos. No, gracias.

M. C. Escher fue un artista que expresó su intriga con perspectivas inusuales que ofrecen una visión de las inversiones en círculos y el modelo de disco de Poincaré para geometría hiperbólica. Uno de sus más famosos es este Autorretrato en un Espejo Esférico. Se trata de un análogo tridimensional de la situación bidimensional que venimos estudiando, inversión del plano euclidiano en círculo. Como siempre ocurre con un espejo, la reflexión en un espejo no es del todo el equivalente matemático porque sólo es una ilusión. Un espejo perfecto en realidad refleja cada punto en 3 espacios al punto del lado opuesto de tal manera que el espejo es el plano que es la bisectriz perpendicular del segmento determinado por el punto y su imagen; simplemente se ve de esa manera. Obviamente, los puntos en el reverso del espejo no forman parte de la escena en absoluto. En el caso esférico de esta obra, los puntos fuera de la esfera parecen estar dentro (aunque obviamente no lo son) y los puntos en el interior no forman parte de la escena en absoluto por lo que la situación no es una transformación, todo el espacio euclidiano tridimensional está “perforado” sino que sigue siendo altamente sugerente del mismo. La situación del plano que hemos estado estudiando sería la de cada plano a través del centro de la esfera y la inversión de la región fuera del círculo de intersección en ese círculo. [www.freakingnews.com/ Escher-Hand-with-Reflecting-Sphere-in-Color-Pics-50737.asp - Usado sin permiso.]

“Límite de círculo IV” de M.C. Escher.

Todas las obras de M.C. Escher

Cordon Art - Baarn - Holanda

plus.maths.org/content/os/issue18/xfile/index Todos los derechos reservados.

Teselado de H.S.M. Coxeter del

Plano Poincaré con triángulos 30-45-90 congruentes

(o$60-45-45$ triángulos isósceles)

mathaware.org/mam/03/ensayo1.html

Todos los derechos reservados.

Por último, ¿por qué la Geometría “Hiperbólica” y cuál es su conexión con el modelo Poincaré? De esta portada de un maravilloso libro sobre la historia de la Geometría Hiperbólica, identificar los puntos correspondientes de un hiperboloide elíptico utilizando como guía el modelo Poincaré: Fuentes de Geometría Hiperbólica, John Stillwell. Una copublicación de la AMS y la London Mathematical Society, History of Math, Vol: 10, Imagen de$1996 .$ portada reproducida con permiso del Dr. Konrad Polthier.