5.2: Conjunto de problemas 5

A menos que se indique lo contrario, asuma todos los axiomas de geometría neutra (aunque no declarada) y también la forma global del Postulado Paralelo Euclideano.

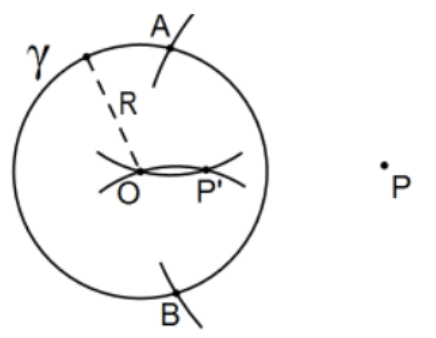
1. Demostrar que es válida la siguiente construcción alternativa de la inversión de un punto dado fuera de un círculo dado en el círculo. No olvides confirmar que$\mathrm{P}^{\prime}$ está en ray OP.

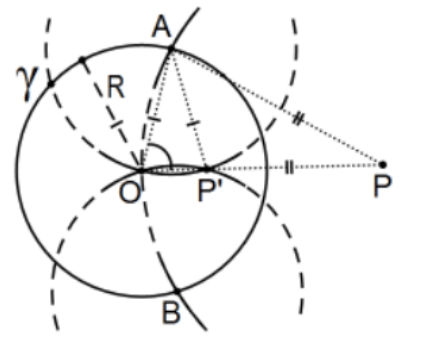
Construcción: Dado el círculo$\gamma=(\mathrm{O}$; R) (es decir, centrado en$\mathrm{O}$ el radio R) y$\mathrm{P}$ fuera del círculo, dejar$\mathrm{A}$ y$\mathrm{B}$ ser determinado por círculo (P; OP) y dejar$\mathrm{P}^{\prime}$ ser determinada por la otra intersección de círculos (A; AO) y (B; BO). Entonces$\mathrm{P}^{\prime}$ está la inversión deseada de$\mathrm{P}$ en el círculo dado$\gamma$.

[Pista: Primero muestra eso$\mathrm{O}, \mathrm{P}$, y$\mathrm{P}^{\prime}$ son colineales (pensar en segmento$\mathrm{AB}$).]

¿Por qué no es esto un teorema en geometría neutra? Es decir, todos los pasos de esta construcción se pueden hacer en geometría neutra entonces ¿por qué restringirse a Euclides?

Nota: Los segmentos de línea punteada en la construcción del segundo boceto no formaban parte de la construcción; solo están ahí para enfatizar su existencia parte de la prueba. El significado de esto es que esta construcción se realizó utilizando únicamente brújula. Un teorema asombroso de la geometría euclidiana (Mohr-Mascheroni) es que todas las construcciones posibles de rectas y brújula se pueden hacer sin la recta! Es decir, aunque dos puntos determinan una línea, la línea en sí no necesita ser parte de la siguiente etapa de la construcción utilizando algún procedimiento alternativo. Para hacerse una idea de lo que esto significa (y lo complicadas que son las cosas), considere intentar construir la intersección de dos líneas, cada una dada por solo dos puntos por cada línea sin dibujar realmente las líneas. La solución implica el hecho de que la inversión de las líneas que se cruzan en un círculo apropiado son círculos que se cruzan con una intersección en el centro del círculo de inversión y siendo la otra la inversión de la intersección de las líneas originales que se pueden construir porque todas estas pueden hacerse con solo una brújula. Finalmente, la inversión de ese punto de intersección de los círculos es la intersección deseada.

El proceso que se acaba de describir requiere la capacidad de hacer inversiones de todos los puntos, no sólo de los que están fuera del círculo como con el Ex 1. Así es como se puede hacer eso: Exactamente la misma prueba funciona si$P$ está dentro del círculo pero más de la mitad “fuera”; es decir,$\mathrm{OP}>\mathrm{R} / 2$. Con una ligera modificación, esto funciona para cualquier$\mathrm{P} \neq \mathrm{O}$. La idea se basa en el hecho de que existe una construcción trivial de círculos solo para duplicar un segmento de línea y, por extensión, cualquier número de veces el segmento a lo largo de la misma línea; es decir, colineal con los 2 puntos originales. La idea es usar la brújula en uno de los puntos, construir el círculo con ese segmento como su radio, y luego “caminar a la mitad del círculo con el mismo radio” que con la construcción trivial de un hexágono regular. Ese punto, digamos$\mathrm{P}_{2}$, es diametralmente opuesto a$\mathrm{O}$ través$\mathrm{P}$ y por lo tanto colineal con ellos duplicando la longitud del segmento OP. Repitiendo el proceso, da cualquier número$n$ de puntos colineales igualmente espaciados. El uso de la técnica de inversión descansa en demostrar que si$P_{n}$ es el punto tal que$\mathrm{OP}_{n}=n(O P)$, luego invertir$P_{n}$ para obtener$P_{n}{ }^{\prime}$$n\left(O O P_{n}{ }^{\prime}\right)=P^{\prime}$, entonces, la inversión del original$P$. En el álgebra, la prueba descansa en el hecho de que si$0<x<R$, entonces$0<(R-x)^{2}$.

2. Casi por definición, si dos círculos son ortogonales, el centro de cualquiera es exterior al otro (ver Nota 2 inmediatamente después de la descripción de las líneas de Poincaré en el Capítulo 3). Por el Teorema Fundamental de los Círculos Ortogonales, podemos decir mucho más. Demostrar que dos círculos que se cruzan son ortogonales si y solo si un punto$\mathrm{P}$ en uno de ellos que está en el interior del otro tiene su centro en la bisectriz perpendicular del segmento de línea$\mathrm{PP}^{\prime}$ donde$\mathrm{P}^{\prime}$ está la inversión de$\mathrm{P}$ en el círculo que contiene$\mathrm{P}$ en su interior.

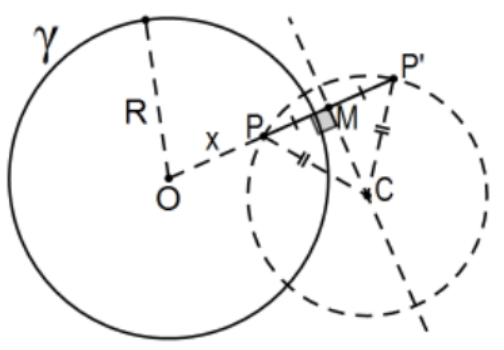
Nota: La prueba de #2 es muy fácil pero es interesante calcular exactamente dónde está esa bisectriz perpendicular en relación con la posición de$\mathrm{P}$ y el radio del círculo. Es decir, calcular la posición del punto medio del segmento de línea en función de$x=m(O P)$ y$R$ en esta figura, el centro del círculo (ortogonal) con diámetro$\mathrm{PP}^{\prime}$.

3. Dejar$A$ y$B$ ser dos puntos en el interior del círculo$\gamma$ centrados en$O$ que no son colineales con$O$ en el modelo Poincaré determinado por el círculo euclidiano$\gamma$. Construir el segmento de línea Poincaré AB.

4. Comenzando con el resultado de #3, construir la inversión isométrica (es decir, congruencia) del modelo Poincaré sobre sí mismo que lleva$A$ a$\mathrm{O}$; es decir,$\mathrm{A}^{\prime}=\mathrm{O}$ y el segmento de línea de Poincaré$\mathrm{A}^{\prime} \mathrm{B}^{\prime}=\mathrm{OB}^{\prime}$, la$(\mathrm{Poincaré}$ congruente) imagen del segmento$A B$ así determinado.
5. Comenzando con el resultado de #4, demostrar que la longitud Poincaré del segmento$A B$ es simplemente$\ln \left(\frac{R+X}{R-X}\right)$ donde$x$ está la longitud euclidiana del segmento$\mathrm{OB}^{\prime}$.

Nota: Las medidas aproximadas se pueden determinar por medición directa (y este cálculo final) pero en geometría teórica, la medición directa “no cuenta”. Todas las “medidas” de ángulo, segmento de línea, área y volumen no son realmente medidas en absoluto; son valores numéricos infinitamente precisos, una imposibilidad con la medición directa. El uso de esto en el$\mathrm{x}, \mathrm{y}$ plano -plano (dado el radio$\mathrm{R}$ y dadas las coordenadas de los puntos interiores$A$ y B) puede producir el valor teóricamente preciso de$x$ como una función de las coordenadas de$A$ y $B$por lo que el valor teóricamente preciso de la longitud de Poincaré del segmento determinado AB. Esto se desarrolla en el Manual de Soluciones junto con un ejemplo numérico.

6. Continuando con #4, deja$\mathrm{C} \neq \mathrm{O}$ ser un tercer punto en el interior de$\gamma$ que no es colineal (en el sentido Poincaré) con A y B. Bosquejo en (o construya cuidadosamente) los segmentos de Poincaré AC y BC para obtener el triángulo de Poincaré$\triangle \mathrm{ABC}$ y completar la congruencia ( preservación isométrica de$=$ distancia y preservación del ángulo) transformación del modelo Poincaré sobre sí mismo que lleva$\mathrm{A}$ a$\mathrm{O}$; es decir,$\mathrm{A}^{\prime}=\mathrm{O}$ y esbozar cuidadosamente$\triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{C}^{\prime}$ la imagen del triángulo $\triangle \mathrm{ABC}$así determinado. [Nota: Esta es la construcción básica en la prueba de SAS para el modelo de disco Poincaré.]

7. Demostrar que, en el plano cartesiano, el círculo de radio 2 centrado en el origen y el círculo de radio$3 / 2$ centrado en$(5 / 2,0)$ son ortogonales. Conoce al menos tres soluciones distintas pero la más fácil es esa$(1)(4)=2^{2}$. ¿Por qué es suficiente ese hecho?
8. Completar la prueba de la desigualdad triangular de la medida de Poincaré en el caso no colineal (desigualdad estricta) completando la prueba indicada en esta figura de que la hipotenusa de un triángulo rectángulo de Poincaré con un vértice de ángulo agudo en el centro del círculo definitorio es mayor que la pierna con uno punto final en el centro. [Pista: Considere el lema de que, para dos segmentos de Poincaré cada uno con un punto final en el centro del círculo definitorio, la longitud Poincaré de uno es mayor que el otro si y solo si la misma desigualdad es cierta para sus longitudes euclidianas (medidas).

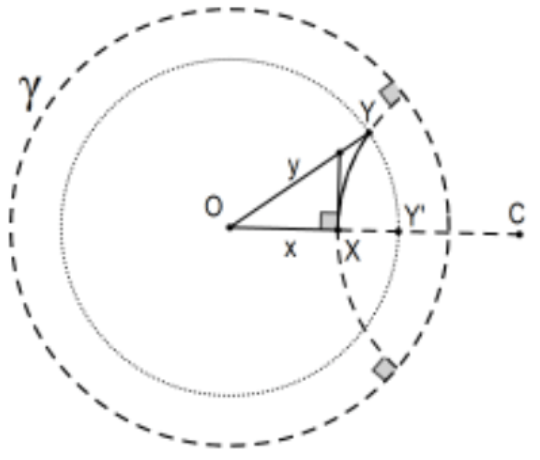
Nota: Para lectores que conocen un poco de topología, la combinación de los casos colineales y no colineales completa la verificación de la desigualdad general del triángulo necesaria para completar la verificación de que la distancia del modelo de Poincaré lo convierte en un espacio métrico. Más allá de eso, la distancia desde$\mathrm{O}$ lo común a lo largo de los radios (use coordenadas polares con el mismo ángulo para el plano x, y con círculo definitorio centrado en el origen) es un homomorfismo del disco de Poincaré al plano x, y. Más explícitamente:

$\sigma$Sea el modelo de disco de Poincaré centrado en$\mathrm{O}$ donde el modelo de los euclides$\varepsilon$ es el$\mathrm{r}, \theta$ plano:$f: \otimes \rightarrow \varepsilon$ vía$f(\mathrm{r}, \theta)=\left(\mathrm{d}_{f}(\mathrm{O},(\mathrm{r}, \theta)), \theta\right)$ es un homomorfismo; es decir, topológicamente, exactamente lo mismo.

9. Dar una prueba analítica de que la inversión de un círculo que no contiene el centro del círculo de inversión es un círculo. [Nota: Nunca lo he hecho sin un análisis complejo pero creo que debe funcionar!]

10. Prueba Caso iv b del “Teorema de Líneas y Círculos”.

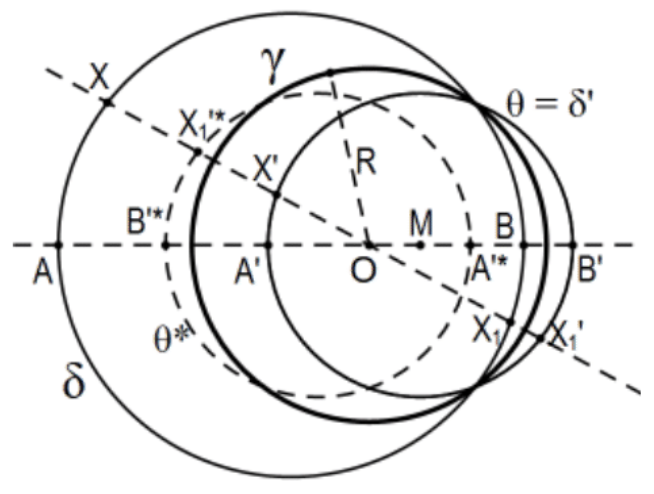
La idea es que la ecuación de la Parte a siga siendo válida pero la inversión resultante no es una dilatación en el sentido habitual sino que está cerca. Si se extiende la dilatación para incluir multiplicadores negativos; es decir, vectores opuestos, la prueba es exactamente la misma. Para la idea habitual de dilatación, tomar lo contrario de cada uno,$X^{\prime *}$, el círculo discontinuo en lugar de la inversión misma. De hecho, el uso de “longitud negativa” cuando se invierte la dirección de un segmento a lo largo de una línea, el hecho de que$\mathrm{O}$ está entre$\mathrm{A}$ e$\mathrm{B}$ implica el cambio de signo por lo que la negatividad del multiplicador$\mathrm{R}^{2} /(\mathrm{OA})(\mathrm{OB})$.

11. Análogamente a las teselaciones del disco Poincaré con infinitamente muchos triángulos congruentes, una esfera (nuestro mundo real) puede ser fácilmente teselada con finitamente muchos. Al igual que con la geometría hiperbólica, existe un teorema de congruencia AAA en la geometría esférica (si los triángulos no son demasiado grandes). Probablemente lo más fácil es considerar el hemisferio norte (ecuador al polo norte) y, en el polo norte, considerar 4 líneas longitudinales a$90^{\circ}$ intervalos$-0^{\circ}, 90^{\circ}, 180^{\circ}$, y$270^{\circ}$. El resultado son ocho triángulos$90^{\circ}-90^{\circ}-90^{\circ}$ congruentes que cubren toda la esfera. Aquí hay algunos otros. Encuentra el tamaño de los ángulos de vértice de cada triángulo de un solo color. [Pista: Mira todos los vértices que se unen para hacer$360^{\circ}$.]

Geometrías, A.B. Sossinsky, AMS Student Mathematical Library No. 64,$2012 .$ De la portada y utilizada sin permiso.

Construcciones euclidianas de puntos y líneas de Poincaré Disk

No debería sorprender que cualquier figura geométrica construible en geometría neutra (es decir, con abstracciones de una recta y brújula) pueda construirse en el modelo de disco de Poincaré para geometría hiperbólica utilizando construcciones estrictamente euclidianas. Algunos de estos ya los hemos hecho y algunos se dan aquí completos con pruebas para ayudar a tener la “sensación” de cómo funciona esto. Por último, hay algunos con a lo sumo pistas sobre cómo comenzar. A continuación, supongamos que el plano Poincaré está$\theta$ determinado por un círculo$\gamma$ centrado en O. Requisito previo Se asumen construcciones euclidianas por lo que se omitirán los detalles a menos que parezcan particularmente útiles o necesarios:

El círculo determinado por tres puntos no colineales.

La tangente a un círculo en un punto sobre él.

Las tangentes a un círculo desde un punto fuera de él.

La inversión en un círculo de un punto dentro o fuera del círculo.

12. La línea Poincaré perpendicular a una línea de Poincaré$\ell$ en un punto$P$ (sea o no$P \in \ell$).

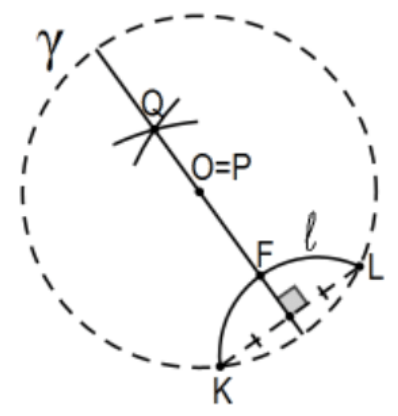
Se presentan dos casos:

Dejar$\mathrm{K}$ y$\mathrm{L}$ ser las intersecciones del círculo euclidiano de la línea Poincaré$\ell$ con el círculo definitorio$\gamma$ con centro en$\mathrm{O}$.

Caso 1:$\mathrm{P}$ es equidistante de$\mathrm{K}$ y$\mathrm{L}$, o

Caso 2: P no es equidistante de$\mathrm{K}$ y$\mathrm{L}$.

Caso 1:$P$ es equidistante de$\mathrm{K}$ y$\mathrm{L}$ y así es$\mathrm{O}$ (radios del círculo definitorio) así que la línea$\mathrm{OP}$ es la bisectriz perpendicular del segmento KL a menos que$\mathrm{P}=\mathrm{O}$ (figura) en cuyo caso construya Q, otro punto equidistante de$K$ y$L$. Entonces la línea$P Q=O Q$ es la bisectriz perpendicular del segmento KL. La línea$P Q=O Q$ es el Poincaré deseado perpendicular a la línea$\ell$.

Prueba: Deja$\mathrm{F}$ ser la intersección de esta línea con$\ell$. Necesitamos saber que la línea PQ es la Poincaré perpendicular a la línea Poincaré$\ell$ pero (por la definición de medida del ángulo de Poincaré) es decir si y sólo si es perpendicular a la tangente euclidiana en el punto F. Sin embargo, obtenemos esto “gratis” porque segmento KL también es un acorde de la Círculo euclidiano que determina la línea Poincaré$\ell$ para que su centro, digamos C, sea equidistante$\mathrm{K}$ y$\mathrm{L}$ así$\mathrm{C}$ también se encuentre en la línea OP. Por lo tanto, la perpendicular euclidiana a$\mathrm{F}$ es perpendicular al radio FC y, por el teorema estándar, esta línea perpendicular es la tangente euclidiana a ese círculo.

Caso 2: Dejar$\mathrm{P}^{\prime}$ ser la inversión de$\mathrm{P}$ in$\gamma$ y dejar que$C$ se determine como la intersección de la bisectriz perpendicular de segmento$\mathrm{PP}^{\prime}$ con la línea KL ya que deben cruzarse. Entonces la línea Poincaré deseada es el arco abierto del círculo indicado$\delta=(C ; C P)$. Por si acaso$P \in l$, la situación es exactamente la misma y lo concluiríamos$\mathrm{F}=\mathrm{P}$.

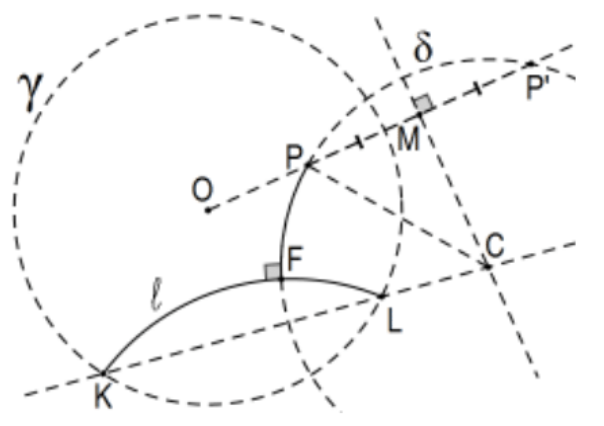
Prueba: La ortogonalidad de$\delta$ con$\gamma$ es inmediata del Teorema Fundamental de los Círculos Ortogonales ya que el rayo OP también contiene$\mathrm{P}^{\prime}$, la inversión de$P$ in$\gamma$. Por definición de la línea Poincaré, el círculo definitorio de la línea Poincaré también$\ell$ es ortogonal a$\gamma$ y el rayo CL también contiene$K$. Nuevamente por el Teorema Fundamental de los Círculos Ortogonales, el círculo de la línea Poincaré también$\ell$ es ortogonal a$\delta$. Es decir, la línea Poincaré en$P$ determinada por el círculo ortogonal (con$\gamma$)$\delta$ es el Poincaré deseado perpendicular a$\ell$ y el punto indicado$F$ es el pie F de la perpendicular Poincaré. Sorprendentemente, ¡tenemos todo lo que necesitamos casi gratis!

13. La perpendicular común a dos líneas paralelas no límite:

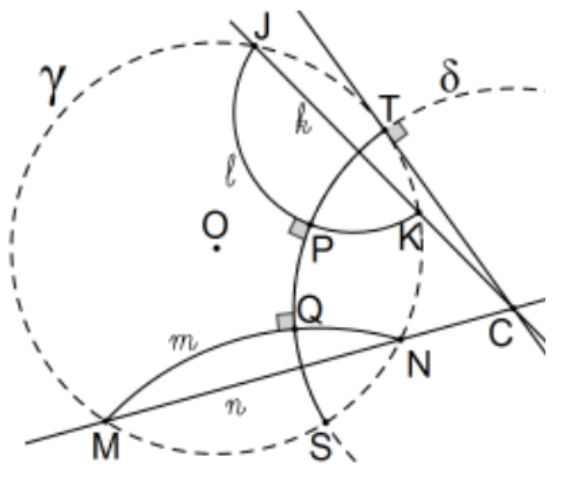
Dejar$l$ y$m$ ser líneas Poincaré y$k$ y$n$ ser las líneas euclidianas de los acordes de los círculos euclidianos (o línea) determinados por$l$ y$m$, respectivamente, con$\gamma$. Si$k$ y$n$ no se cruzan, es decir, son paralelos euclidianos, la línea es el diámetro de los bisectores perpendiculares comunes de los acordes. Si$k$ y se$n$ cruzan, digamos$\mathrm{C}$, este es el centro del círculo deseado y el punto de tangencia de éste a cualquiera de los arcos del círculo euclidiano$\gamma, l$, o$m$, por ejemplo$\mathrm{T}$, determina el radio así$\delta=(\mathrm{C} ; \mathrm{CT})$ determina la línea Poincaré deseada$\mathrm{PQ}$.

Prueba: Dado que la línea euclidiana CT es tangente a$\gamma$, el nuevo círculo es ortogonal para que se determine una línea Poincaré. Ortogonalidad con$l$ y$m$ es inmediata como en el Ej. $12 .$

14. El límite es paralelo a línea$l$ en punto,$\mathbf{p}$ no en$\ell$:

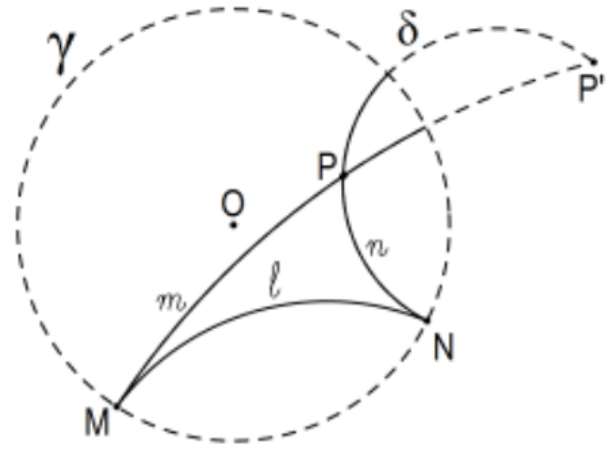
Caso 1: Si$\mathrm{P}=\mathrm{O}$, las líneas deseadas son los diámetros obvios.

Caso 2:$P \neq O$, deje$\mathrm{P}^{\prime}$ ser la inversión$\mathrm{P}$ en$\gamma$ obtener$\mathrm{P}^{\prime}$.

Dejar$M$, y$N$ ser los puntos determinados por la extensión (círculo o línea euclidiana) de$\ell$ con$\gamma$. Los círculos euclidianos (es decir, las líneas de Poincaré) son los determinados por$\mathrm{P}, \mathrm{P}^{\prime}$, y$\mathrm{M}$ o$\mathrm{N}$.

Nota: Esta es la misma construcción que la de la línea Poincaré determinada por dos puntos Poincaré excepto que uno de ellos es ahora un punto límite en lugar de uno de los puntos interiores.

15. La bisectriz perpendicular de un segmento de línea Poincaré:

Dejar$A$ y$B$ ser los puntos finales del segmento dado de Poincaré:

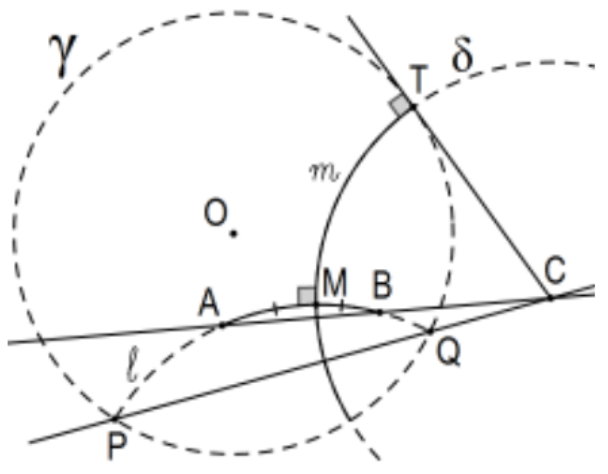
Caso 1:$\mathrm{OA} \cong \mathrm{OB}$. Trivial; es la bisectriz perpendicular de la cuerda euclidiana AB. (No hay punto$C$ en la figura.)

Caso 2:$\mathrm{A}, \mathrm{B}$, y$\mathrm{O}$ colineal. En este caso, el segmento de Poincaré$\mathrm{AB}$ es el mismo conjunto que el segmento euclidiano$A B$ y el círculo de Poincaré con diámetro$\mathrm{AB}$ es el mismo conjunto que el círculo euclidiano con el mismo diámetro por lo que primero construye el círculo euclidiano con ese diámetro (punto medio y ...) y finalmente su centro Poincaré (Ex 17).

Caso 3: A, B y$\mathrm{O}$ no colineales. Las líneas euclidianas$\mathrm{AB}$ y no$\mathrm{PQ}$ son paralelas (eso fue Caso 1) así que dejó$C$ ser su intersección. Proceder como se indica.

16. La línea de reflexión Poincaré (es decir, círculo euclidiano de inversión) que lleva un punto dado a otro punto dado: Esto generaliza el importante caso especial de reflejar un punto al centro del círculo definitorio. [Pista: Exactamente Ex. 15, A a B o equivalentemente, B a A.]

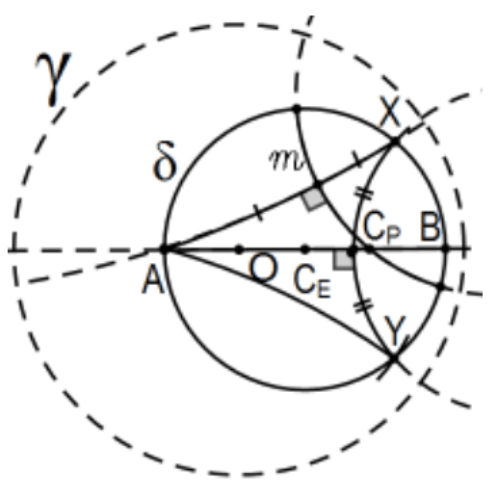
17. El centro Poincaré de un círculo Poincaré:

Una solución natural pero tediosa es usar el Ej. 14 y seguir la construcción estándar (geometría neutra). Es decir, elegir cuatro puntos cualesquiera (o tres es más común) para determinar dos acordes de Poincaré siendo el centro la intersección de los círculos de Poincaré. Una solución mucho más fácil es “engañar” construyendo primero su centro euclidiano y, al usar la línea de centros para ser uno de los bisectores perpendiculares, podemos salir adelante con una sola cuerda.

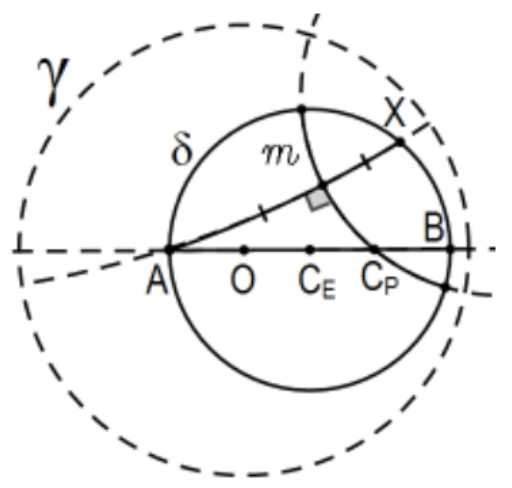
Construcción:$\mathrm{O}$ Sea el centro del círculo definitorio$\gamma$ y deje$C_{E}$ ser el centro euclidiano del círculo Poincaré. Si$O=C_{E}$, estamos hechos así suponemos que determinan una línea y dejan$\mathrm{A}$ y$\mathrm{B}$ sean sus intersecciones con el círculo en cuestión. $\mathrm{X}$Sea cualquier otro punto de círculo. Construir la línea Poincaré determinada por A y X y la bisectriz perpendicular$m$ del segmento de Poincaré$\mathrm{AX}$ (Ej. 15). La intersección de$m$ y diámetro$\mathrm{AB}, \mathrm{C}_{\mathrm{P}}$, es el centro Poincaré del círculo. La segunda construcción es la misma pero usando BX en lugar de AX. Como se describe en la prueba a continuación, existe una ventaja práctica cuando los puntos A y B están así posicionados.

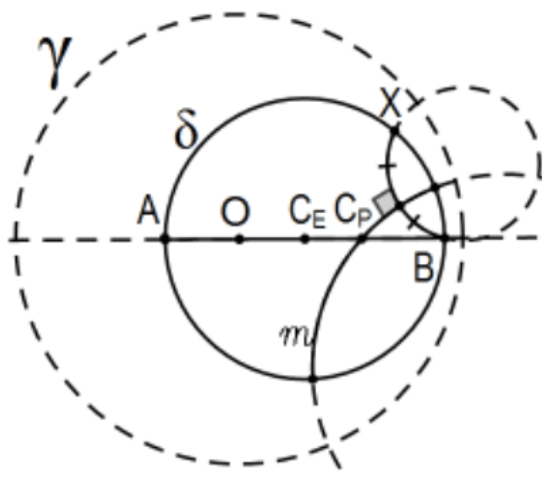
Prueba: El hecho de que el centro Poincaré esté en el diámetro de los centros euclidianos será consecuencia de la prueba y se basa en elegir cuidadosamente los 3 puntos para 2 acordes Poincaré de los cuales los bisectores perpendiculares de Poincaré deben cruzarse para determinar el centro por geometría neutra consideraciones. La idea es utilizar$X$ y$A$ (o B) para determinar uno de los acordes y segmento euclidiano$\mathrm{OX}$ (o$\mathrm{AX}$ o$B X$) para balancear un arco para establecer$Y$ como la reflexión euclidiana de $X$en la línea de centros. Completamente por simetría, la bisectriz perpendicular Poincaré de Poincaré acorde AY (o BY) debe cruzarse en el mismo punto,$C_{p}$.

$\underline{\text { Note 1: }}$La construcción de la línea Poincaré AX es particularmente desordenada porque está tan cerca de$\mathrm{O}$ que el centro del círculo euclidiano de la línea Poincaré está lejos de la página tan difícil de construir físicamente con herramientas euclidianas o incluso de ver realmente (en una práctica sentido, no teórico) la ubicación de su centro. Elegir BX en su lugar lo hace mucho más claro.

$\underline{\text { Note 2: This construction can be used to construct the Poincaré midpoint of a line segment AB when A and }$$\mathrm{B}$son colineales con$\mathrm{O}$. La idea es construir su punto medio euclidiano y el círculo euclidiano con diámetro AB. Por último, elija cualquier$X$ otro punto del círculo, y siga la misma construcción. Entonces$C_{p}$ es el punto medio Poincaré de AB.

18. El Círculo dado su Centro y Radio Poincaré:

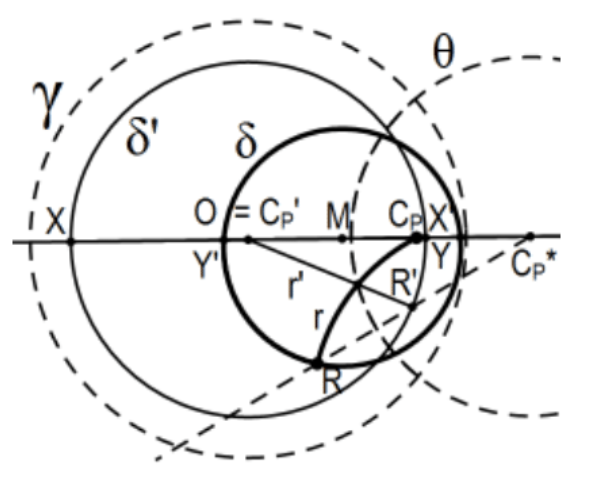
Construcción: Dejar$\mathrm{O}$ ser el centro del círculo definitorio$\boldsymbol{\gamma}$ y dejar que$C_{\mathrm{p}}$ sea el centro de Poincaré y el segmento de Poincaré$C_{\mathrm{p}} \mathrm{R}=\mathrm{r}$ sea el radio del círculo de Poincaré determinado$\delta=\left(C_{\mathrm{p}} ; \mathrm{C}_{\mathrm{p}} \mathrm{R}\right)$ para ser construido utilizando Herramientas euclidianas, todas indicadas en negrita. Primero, construir$\theta$, inversión en la que lleva$C_{p}$ a$O, O=C_{p}{ }^{\prime}$. También lleva$\mathrm{R}$ a$\mathrm{R}^{\prime}$ eso debe mentir$\delta^{\prime}$, la inversión de$\delta$ in$\theta$. construcción de$\delta^{\prime}=\left(\mathrm{O} ; \mathrm{OR}^{\prime}\right)=\left(\mathrm{O} ; \mathrm{r}^{\prime}\right)$ es una trivialidad y, dejar$\mathrm{X}$ y$\mathrm{Y}$ ser las intersecciones de$\delta^{\prime}$, tenemos un diámetro, cuya inversión en$\theta, X^{\prime}$ y$Y^{\prime}$, debe ser un diámetro del círculo deseado$\delta$. Ahora tenemos dos formas de terminar la construcción, ya sea usar los 3 puntos de$\delta$ saber que es un círculo euclidiano$X^{\prime}$,$Y^{\prime}$, y$R$, o construir el punto medio euclidiano$M$ del segmento $X^{\prime} Y^{\prime}$y tenemos$\delta=(M$,$\left.M^{\prime}\right)=\left(M, M^{\prime}\right)$

19. Teorema: Un conjunto de puntos Poincaré es un círculo Poincaré si y solo si se trata de un círculo euclidiano que se encuentra completamente dentro del círculo definitorio.

20. El Bisectriz Poincaré de un Ángulo Poincaré:

Aquí hay dos soluciones. Refleja el vértice hacia el centro y sigue un punto en cada rayo... O construya las tangentes euclidianas a cada línea de Poincaré en el vértice y biseccione el ángulo euclidiano resultante. Finalmente, construya el círculo ortogonal a través de ese punto y tangente al ángulo bisectriz.

Nota: Una vez que tienes una idea de cómo va esto, los más complicados no son tan difíciles pero incluso copiar un segmento de línea o un ángulo es más complicado de lo que piensas pero son absolutamente críticos para la prueba de que el Disco Poincaré es un modelo para geometría hiperbólica. Aquí hay un ejemplo:

21. Las tangentes a un Círculo Poincaré P fuera del Círculo:

La solución más obvia es seguir la construcción de geometría neutra (PS 2, #25 como se muestra en PS 3, #25) ya que ahora se ha presentado cada una de las construcciones euclidianas necesarias. Otro enfoque es la idea de invertir un punto crítico para$\mathrm{O}$, hacer el trabajo, y luego invertir de nuevo, una técnica común que se ha utilizado antes (e.g., SAS).

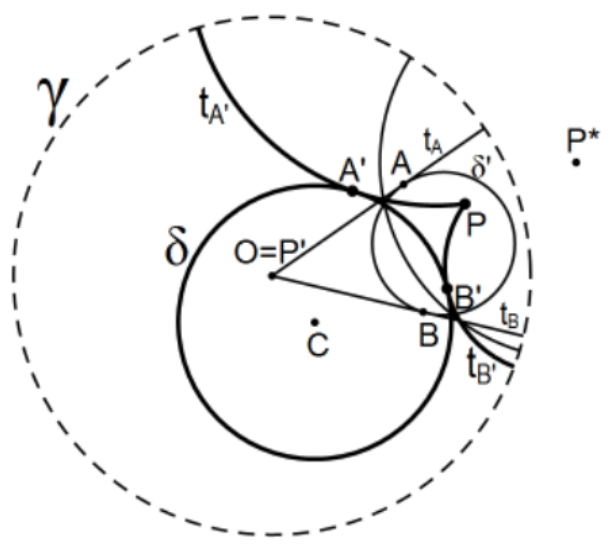
La idea es elegir el punto crítico para mapear al centro del círculo definitorio por inversión en una línea apropiada de Poincaré. Que el círculo sea el que tenga el centro Poincaré C (C no se usa en la construcción euclidiana - ver detalles abajo) y P sea el punto a partir del cual se van a construir las tangentes y la línea apropiada de Poincaré es la centrada en la inversión de$P$ en el círculo definitorio, digamos $\mathrm{P}^{*}$(no representado aquí) para no confundirlo con inversiones en este nuevo círculo) con el radio determinado por la Euclidiana *perpendicular$\mathrm{P}$ al rayo$\mathrm{OP}$ donde$\mathrm{O}$ está el centro del círculo definitorio. Este círculo determina, el arco pasante$\mathrm{M}$, la bisectriz perpendicular de Poincaré del segmento lineal OP, la línea que refleja$P$ a O. Reflejando el círculo en esta línea (es decir, inversión en este círculo euclidiano), su reflejo será otro círculo pero, esta vez, el punto en cuestión es el centro del círculo definitorio de manera que sus tangentes euclidianas son también sus tangentes Poincaré, puntos$A$ y en$B$. la figura. Invertiendo$A$ y$B$ en la misma línea obtenemos los puntos de tangencia,$\mathrm{A}^{\prime}$ y$\mathrm{B}^{\prime}$. Usando$\mathrm{P}^{*}$, tenemos tres puntos para construir cada uno de los círculos euclídeos ortogonales necesarios; es decir, cada uno de los círculos determinados por$\mathrm{P}^{\prime} \mathrm{A}^{\prime}$, y$\mathrm{P}^{*}$ y$\mathrm{P}, \mathrm{B}^{\prime}$, y$\mathrm{P}^{*}$. Estos arcos son las tangentes deseadas ya que conservan la ortogonalidad con los radios de Poincaré en$A$ y B.

En realidad hacer esto sin la ayuda de Cenicienta, incluso con la ayuda del Bloc de bocetos de Geometer, se vuelve un poco desordenado: Como último ejercicio en el Capítulo 4, comenzamos con$\alpha$, un círculo que contiene$O$, el centro del círculo definitorio solo para mostrar cómo el centro se invierte afuera como$P$ se invierte a$O$. ¿Cómo hacer eso? Que C sea su centro euclidiano (en lugar de su centro Poincaré en la imagen de arriba) y considere los puntos X y$\mathrm{Y}$ (no representados) determinados por el rayo$\mathrm{P} * \mathrm{C}$, un diámetro euclidiano del círculo. Invertir$\mathrm{X}$ y$\mathrm{Y}$ en el círculo inversor para obtener$\mathrm{X}^{\prime}$ y$\mathrm{Y}^{\prime}$ que debe ser un diámetro del círculo invertido. Ahora el punto medio euclidiano$M$ del segmento$\mathrm{X}^{\prime} \mathrm{Y}^{\prime}$ con cualquiera de los dos puntos para el radio determina el círculo invertido completo$\alpha^{\prime}$. Las tangentes Poincaré desde$\mathrm{O}=\mathrm{P}^{\prime}$ este nuevo círculo son exactamente las mismas que las euclidianas así que determinan los puntos tangentes euclidianos$A$ y$B$ del círculo invertido. Estos son también los puntos tangentes Poincaré así que invertirlos de nuevo al círculo original$A^{\prime}$ y$B^{\prime}$. Los círculos euclidianos determinados por$P, A^{\prime}$, y$P^{*}$ y$P$$\mathrm{B}^{\prime}$, y$\mathrm{P}^{*}$ determinan las líneas tangentes de Poincaré deseadas.

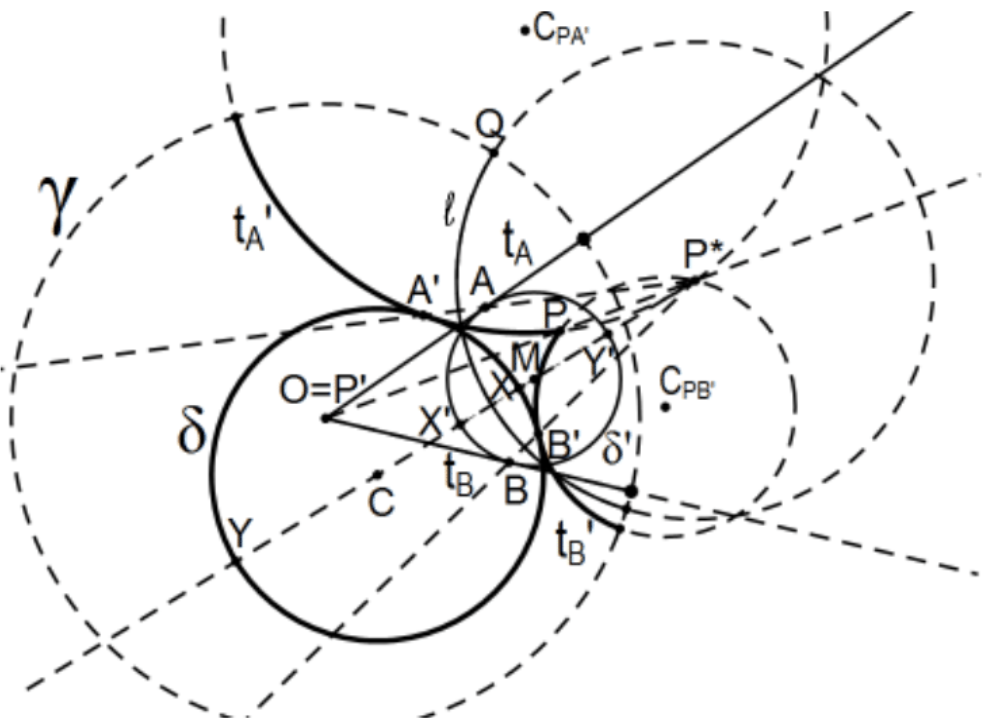
Confundir, ¿no? En lo anterior, el círculo definitorio es$\gamma$ el círculo grande de la izquierda con centro$\mathrm{O}$ y el círculo dado es el círculo más grande$\alpha$ que contiene en$\mathrm{O}$ su interior con centro euclidiano$\mathrm{C}$, y el punto $\mathrm{P}$fuera de ese círculo, a partir del cual se van a construir las tangentes Poincaré, está en el lío en el medio. La perpendicular al rayo$\mathrm{OP}$ en$\mathrm{P}$ establece$\mathrm{Q}$ y la intersección de la tangente en$\mathrm{Q}$ con el rayo$\mathrm{OP}$ establece$\mathrm{P}^{*}$, la inversión de$P$ en $\gamma$. El círculo centrado en$P^{*}$ de radio$P * Q$ establece la línea de Poincaré$\ell$, la reflexión en la que$\mathrm{P}$ se lleva a$\mathrm{O}=\mathrm{P}^{\prime}$. El reflejo del plano Poincaré en esta línea lleva el círculo en cuestión a otro círculo dentro del círculo definitorio. Una forma de establecer ese círculo reflejado es reflejar los puntos$\mathrm{X}$ diametrales y$\mathrm{Y}$ establecidos por el rayo$\mathrm{P}{ }^{*} \mathrm{C}$ para establecer puntos diametrales del círculo invertido$X^{\prime}$ y$Y^{\prime}$. El centro euclidiano de este círculo (también Poincaré)$M$ es solo el punto medio euclidiano del segmento$X^{\prime} Y^{\prime}$ necesario para construir$\alpha^{\prime}$, el reflejo del círculo$\alpha$ en línea$\ell$ y para construir puntos $A$y$B$, los puntos euclidianos de tangencia desde$\mathrm{O}$ hasta$\alpha^{\prime}$, de ahí las tangentes euclidianas a$\alpha^{\prime}$ sí mismas (incluidas aquí pero realmente no utilizadas en la construcción). Reflejando$A$ y$B$ en la línea inversadora$l$ para establecer$\mathrm{A}^{\prime}$ y$\mathrm{B}^{\prime}$ sobre el círculo original$\alpha$, hemos determinado los puntos de tangencia (ya que la inversión en un círculo conserva ángulos incluyendo ortogonalidad que establecerán tangencia Poincaré). Dado que A', P, P* deben estar en el círculo euclidiano, podemos construir el círculo construyéndolo en el centro$\mathrm{C}_{\mathrm{PA}^{\prime}}$ (fuera de la parte superior de la figura) y el arco del círculo es el rayo tangente de Poincaré$\mathrm{PA}^{\prime}$ y de manera similar$\mathrm{C}_{\mathrm{PB}^{\prime}}$ (se muestra) y las tangentes de Poincaré se construyen.