APÉNDICE - Prueba del Teorema Z

Última actualización
Guardar como PDF

Page ID: 114709

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En la sección 1.4 afirmamos pero no probamos el siguiente teorema:

Teorema$\PageIndex{1}$ (The "Z" Theorem)

Si dos líneas son paralelas entonces sus ángulos interiores alternos son iguales. Si los ángulos interiores alternos de dos líneas son iguales entonces las líneas deben ser paralelas.

Teorema$\PageIndex{1}$ consta de dos declaraciones, cada una la conversa de la otra, Vamos a probar la segunda declaración primero:

Teorema$\PageIndex{1}$ (second part).

Si los ángulos interiores alternos de dos líneas son iguales entonces las líneas deben ser paralelas. En la Figura$\PageIndex{1}$, if $\angle x = \angle x'$ then $\overleftrightarrow{AB}$ must be parallel to $\overleftrightarrow{CD}$.

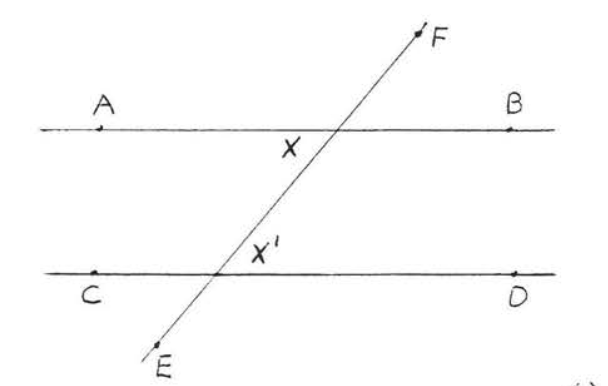
$Screen Shot 2021-01-19 a las 8.50.29 PM.png$

Figura$\PageIndex{1}$. We will prove that if $\angle x = \angle x'$ then $\overleftrightarrow{AB}$ is parallel to $\overleftrightarrow{CD}$.

Proof

Suppose $\angle x = \angle x'$ and $\overleftrightarrow{AB}$ is not parallel to $\overleftrightarrow{CD}$. This means that $\overleftrightarrow{AB}$ and $\overleftrightarrow{CD}$ meet at some point $G$, as in Figure $\PageIndex{2}$, forming a triangle, $\triangle KLG$.

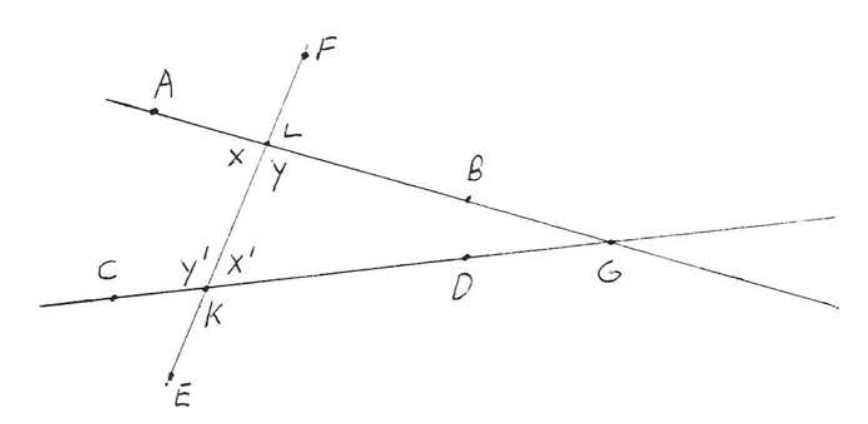
$Screen Shot 2021-01-19 at 8.57.36 PM.png$

Figure $\PageIndex{2}$. If $\overleftrightarrow{AB}$ is not parallel to $\overleftrightarrow{CD}$ then they must meet at some point $G$.

We know from the discussion preceding the ASA Theorem (THEOREM 2.3.1, section 2.3) that $\triangle KLG$ can be constructed from the two angles $\angle x'$ and $\angle y$ and the included side $KL$. Now $\angle x = \angle x'$ (by assumption) and $\angle y' = \angle y$ ($\angle y' = 180^{\circ} - \angle x' = 180^{\circ} - \angle x = \angle y$). Therefore by the same construction $\angle x$ and $\angle y'$ when extended should yield a triangle congruent to $\triangle KLG$. Call this new triangle $\triangle LKH$ (see Figure $\PageIndex{3}$). We now have that $\overleftrightarrow{AB}$ and $\overleftrightarrow{CD}$ are both straight lines through $G$ and $H$. This is impossible since one and only one distinct straight line can be drawn through two points. Therefore our assumption that $\overleftrightarrow{AB}$ is not parallel to $\overleftrightarrow{CD}$ is incorrect, that is, $\overleftrightarrow{AB}$ must be parallel to $\overleftrightarrow{CD}$. This completes the proof.

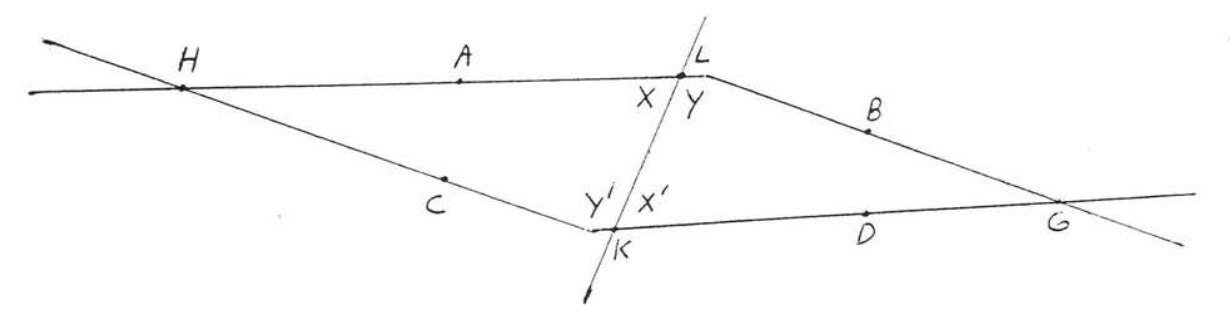
$Screen Shot 2021-01-19 at 9.04.21 PM.png$

Figura$\PageIndex{3}$. Desde$\angle x = \angle x'$ y$\angle y' = \angle y$,$\angle x$ y$\angle y'$ cuando se extiende también debe formar un triángulo,$\triangle LXH$.

Teorema$\PageIndex{1}$ (first part)

Si dos líneas son paralelas entonces sus ángulos interiores alternos son iguales. En la Figura$\PageIndex{4}$, if $\overleftrightarrow{AB}$ is parallel to $\overleftrightarrow{CD}$ then $\angle x = \angle x'$.

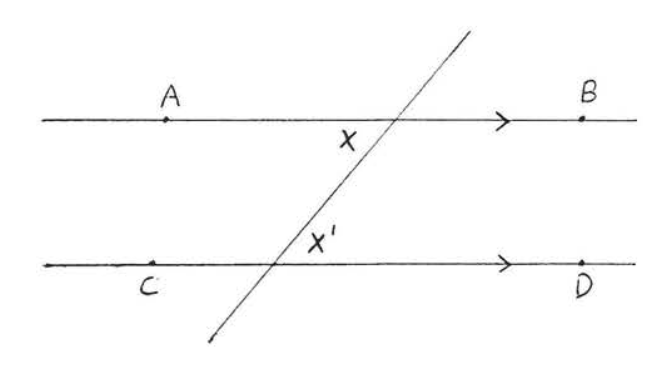
$Screen Shot 2021-01-19 a las 9.10.19 PM.png$

Figura$\PageIndex{4}$. We will prove that if $\overleftrightarrow{AB}$ is parallel to $\overleftrightarrow{CD}$ then $\angle x = \angle x'$.

Proof

Suppose $\overleftrightarrow{AB}$ is parallel to $\overleftrightarrow{CD}$ and $\angle x \ne \angle x'$. One of the angles is larger; suppose it is $\angle x$ that is larger. Draw $\overleftrightarrow{EF}$ through $P$ so that $\angle w = \angle w'$ as in Figure $\PageIndex{5}$. $\overleftrightarrow{EF}$ is parallel to $\overleftrightarrow{CD}$ because we have just prove (THEOREM $\PageIndex{1}$, second part) that two lines are parallel if their alternate interior angles are equal. This contradicts the parallel postulate (section 1.4) which states that through a point not on a given line (here point $P$ and line $\overleftrightarrow{CD}$) one and only one line can be drawn parallel to the given line. Therefore $\angle x$ must be equal to $\angle x'$. This completes the proof of THEOREM $\PageIndex{1}$.

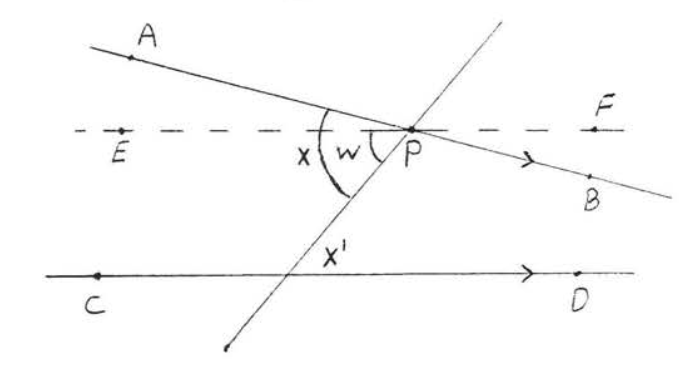
$Screen Shot 2021-01-19 at 9.15.34 PM.png$

Figura$\PageIndex{5}$. Draw $\overleftrightarrow{EF}$ so that $\angle w = \angle w'$.

Teorema\(\PageIndex{1}\) (The "Z" Theorem)

Teorema\(\PageIndex{1}\) (second part).

Teorema\(\PageIndex{1}\) (first part)