Respuestas a problemas de números impares

Última actualización
Guardar como PDF

Page ID: 114720

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Sección 1.1

1. 6

3. $x = 9$,$AC = 24$.

5. 15

7. 3

Sección 1.2

1. $\angle CBD$o$\angle DBC$

3. $\angle AED$o$\angle DEA$

5. $\angle ABC$o$\angle CBA$

7. $70^{\circ}$

9. $x = 130^{\circ}$,$y = 50^{\circ}$

11. $x = 30^{\circ}$,$y = 60^{\circ}$

13. $\angle A = 60^{\circ}$,$\angle B = 50^{\circ}$,$\angle C = 70^{\circ}$

15. $\angle A = 110^{\circ}$,$\angle B = 80^{\circ}$,$\angle C = 70^{\circ}$,$\angle D = 100^{\circ}$

17.

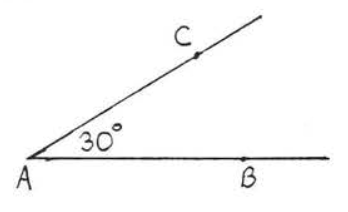
$Screen Shot 2021-01-21 a las 10.57.58 AM.png$

19.

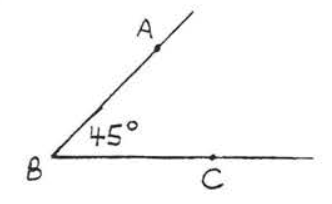
$Screen Shot 2021-01-21 a las 10.58.22 AM.png$

21.

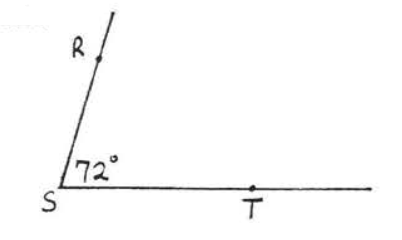
$Screen Shot 2021-01-21 a las 10.58.55 AM.png$

23.

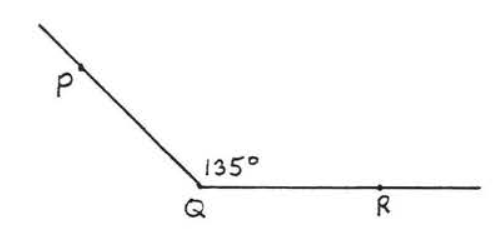
$Screen Shot 2021-01-21 a las 10.59.03 AM.png$

25. $35^{\circ}$

27. $30^{\circ}$

Sección 1.3

1. a)$53^{\circ}$ b)$45^{\circ}$ c)$37^{\circ}$ d)$30^{\circ}$

3. $15^{\circ}$

5. $30^{\circ}$

7. a)$150^{\circ}$ b)$143^{\circ}$ c)$90^{\circ}$ d)$60^{\circ}$

9. $30^{\circ}$

11. $x = 3, -3$

13. 10

15. $x = 70, y = 110, z = 70$

17. $x = 30, y = 45, z = 105$

19. $x = y = z = 90$

21. $x = 40, y = 80, z =100$

23. 8, -8

25. 4, -5

27. $45^{\circ}$

Sección 1.4

1. $x = 50, y = z= 130$

3. $u = x = z = 120, t = v = w = y = 60$

5. 55

7. 50

9. 50

11. 55

13. 60

15. 37

17. 11

19. interior alternativo:$\angle ABD$ &$\angle CDB - AB||CD$;$\angle ADB$ &$\angle CBD - AD||BC$

21. correspondiente:$\angle BAC$ &$\angle EDC - AB||DE$;$\angle ABC$ &$\angle DEC - AB||DE$

23. interior en el mismo lado de transversal:$\angle BAD$ &$\angle CDA - AB||CD$;$\angle ABC$ &$\angle DCB - AB||CD$

25. interior alternativo:$\angle BAC$ &$\angle DCA - AB|| DE$;$\angle ABC$ &$\angle ECB - AB||DE$

27. $65^{\circ}$

Sección 1.5

1. $85^{\circ}$

3. $37^{\circ}$

5. $60^{\circ}$

7. 30

9. 6

11. 120

13. $x = 50, y = 40, z = 50$

15. $65^{\circ}$

17. 8

19. 24

21. $720^{\circ}$

23. $60^{\circ}$

25. $108^{\circ}$

Sección 1.6

1. 2/3

3. 6

5. $x = 1, AB = 2$

7. $x = 9, \angle ACB = 90^{\circ}$

9. $\dfrac{25x + 11}{6}, \dfrac{37}{2}$

11. 5

Sección 2.1

1. $AB = DE, BC = EF, AC = DF, \angle A = \angle D$,$\angle B = \angle E, \angle C = \angle F, x = 5, y = 6$

3. $AB = CD, BC = DA, AC = CA, \angle BAC = \angle DCA, \angle B = \angle D, \angle BCA = \angle DAC, x = 55, y = 35$

5. $\triangle PQR \cong \triangle STU$

7. $\triangle ABC \cong \triangle ABD$

9. $\triangle ABD \cong \triangle CDB$

Sección 2.2

1. $BC = 1.7$,$\angle = 30^{\circ}$,$\angle C = 90^{\circ}$

3. $BC = 1.95, \angle B = 99^{\circ}, \angle C = 41^{\circ}$

5. $\angle B$

7. $\angle D$

9. (1)$AC, \angle A, AB$$\triangle ABC = DF, \angle D, DE$ de$\triangle DEF$

(2)$\triangle ABC \cong \triangle DEF$

(3)$x = 65, y = 45$

11. (1)$AB, \angle B, BC$$\triangle ABC = EF, \angle F, FD$ de$\triangle EFD$

(2)$\triangle ABC \cong \triangle EFD$

(3)$x = 40, y = 50$

13. (1)$AB, \angle B, BC$$\triangle ABC = ED, \angle D, DF$ de$\triangle EDF$

(2)$\triangle ABC \cong \triangle EDF$

(3)$x = 8$

15. (1)$AB, \angle B, BC$$\triangle ABC = ED, \angle D, DF$ de$\triangle EDF$

(2)$\triangle ABC \cong \triangle EDF$

(3)$x = 20, y = 30$

17. (1)$BA, \angle A, AC$$\triangle ABC = DC, \angle C, CA$ de$\triangle CDA$

(2)$\triangle ABC \cong \triangle CDA$

(3)$x = 22$

19. (1)$AC, \angle ACD, CD$$\triangle ACD = BC, \angle BCD, CD$ de$\triangle BCD$

(2)$\triangle ACD \cong \triangle BCD$

(3)$x = 50$

21. (1)$AD, \angle ADC, DC$$\triangle ACD = BD, \angle BDC, DC$ de$\triangle BCD$

(2)$\triangle ACD \cong \triangle BCD$

(3)$x = 2$

23. (1)$BC, \angle BCA, CA$$\triangle ABC = DC, \angle DCE, CE$ de$\triangle EDC$

(2)$\triangle ABC \cong \triangle EDC$

(3)$x = 20, y = 10$

25. (1)$AC, \angle ACB, CB$$\triangle ABC = EC, \angle ECD, CD$ de$\triangle EDC$

(2)$\triangle ABC \cong \triangle EDC$

(3)$x = 70$

Sección 2.3

1. $BC = 1.9, AC = 2.3, \angle C = 90^{\circ}$

3. $BC = 2.3, AC = 1.9, \angle C = 90^{\circ}$

5. $AB$

7. $DF$

9. (1)$\triangle ABC \cong \triangle DEF$

(2)$ASA = ASA$:$\angle A, AB, \angle B$$\triangle ABC = \angle D, DE, \angle E$ de$\triangle DEF$

(3)$x = 5, y = 6$

11. (1)$\triangle RST \cong \triangle UWV$

(2)$AAS = AAS: \angle T, \angle R, RS$$\triangle RST = \angle V, \angle U, UW$ de$\triangle UWV$

(3)$x = 7, y = 6$

13. (1)$\triangle ABD \cong \triangle CDB$

(2)$ASA = ASA: \angle B, BD, \angle D$$\triangle ABD = \angle D, DB, \angle B$ de$\triangle CDB$

(3)$x = 30, y = 25$

15. (1)$\triangle ABC \cong \triangle EDC$

(2)$ASA = ASA: \angle A, AC, \angle ACB$$\triangle ABC = \angle E, EC, \angle ECD$ de$\triangle EDC$

(3)$x = 11, y = 9$

17. (1)$\triangle ACD \cong \triangle BCD$

(2)$AAS = AAS: \angle A, \angle ACD, CD$$\triangle ACD = \angle B, \angle BCD, CD$ de$\triangle BCD$

(3)$x = 5, y = 5$

19. (1)$\triangle ABC \cong \triangle EDC$

(2)$ASA = ASA: \angle B, BC, \angle BCA$$\triangle ABC = \angle D, DC, \angle DCE$ de$\triangle EDC$

(3)$x = 2, y = 3$

21. (1)$\triangle ABC \cong \triangle EDF$

(2)$ASA = ASA: \angle B, BC, \angle C$$\triangle ABC = \angle D, DF, \angle F$ de$\triangle EDF$

(3)$x = 2, y = 3$

23. $\triangle PTB \cong \triangle STB$,$ASA = ASA: \angle PTB, TB, \angle TBP$$\triangle PTB = \angle STB, TB, \angle TBS$ de$\triangle STB$. $SB = PB = 5, SP = SB + BP = 5 + 5 = 10$.

25. $\triangle DEC \cong \triangle BAC$,$ASA = ASA: \angle E, EC, \angle ECD$$\triangle DEC = \angle A, AC, \angle ACB$ de$\triangle BAC. AB = ED = 7$.

Sección 2.4

1. $\angle A = \angle D$dado,$AB = DE$ dado,$\angle B = \angle E$ dado,$\triangle ABC \cong \triangle EDF$. (ASA = ASA, AC = DF\) los lados correspondientes de$\cong \triangle$'s son =.

3. $AC = EC$dado,$\angle ACB = \angle ECD$ verticales$\angle$,$BC = DC$ dado,$\triangle ABC \cong \triangle EDC$. $SAS = SAS, AB = ED$lados correspondientes de$\cong \triangle$'s son =.

5. $\triangle ABD = \angle CDB$dado,$BD = DB$ identidad,$\angle ADB = CBD$ dado,$\triangle ABD \cong \triangle CDB$. $ASA = ASA, AB = CD$lados correspondientes de$\cong \triangle$'s son =.

7. $AC = BC$dado,$\angle ACD = \angle BCD$ dado,$CD = CD$ identidad,$\triangle ACD \cong \triangle BCD$. $SAS = SAS, \angle A = \angle B$correspondientes de$\angle$$\cong \triangle$'s son =.

9. $\angle BAE = \angle DCE$los interiores alternos$\angle$ de$||$ las líneas son =,$AB = CD$ dado, los interiores$\angle ABE = \angle CDE$ alternos$\angle$ de$||$ las líneas son =,$\triangle ABE \cong \triangle CDE$. $ASA = ASA$, los lados$AE = CE$ correspondientes de$\cong \triangle$'s son =.

11. $\angle ABC = \angle DCE$correspondientes$\angle$ de$||$ líneas son =,$\angle A = \angle D$ dar,$AC = DE$ dado,$\triangle ABC \cong \triangle DCE$. $AAS = AAS$, los lados$BC = CE$ correspondientes de$\cong \triangle$'s son =.

13. $AD = BC$dado,$\angle BAD = \angle ABC$ dado,$AB = BA$ identidad,$\triangle ABD \cong \triangle BAC$. $SAS = SAS$, los lados$AC = BD$ correspondientes de$\cong \triangle$'s son =.

Sección 2.5

1. 35

3. 7

5. 45

7. $x = 18, \angle A = \angle B = 52^{\circ}, \angle C = 76^{\circ}$

9. $x = 4, AB = 24, AC = BC = 21$

11. $x = 1, y = 4, AC = 10$

13. 125

Sección 2.6

1. $\triangle ABC \cong \triangle FDE$,$SSS = SSS: AB, BC, AC$$\triangle ABC = FD, DE, FE$ de$\triangle FDE, x = 30, y = 70, z = 80$

3. $\triangle ABD \cong \triangle CDB$,$SSS = SSS: AB, BD, AD$$\triangle ABD = CD, DB, CB$ de$\triangle CBD, x = 70, y = 50, z = 60$

5. $\triangle ABC \cong \triangle EDC$,$SAS = SAS: AC, \angle ACB, CB$$\triangle ABC = EC, \angle ECD, CD$ de$\triangle EDC, x = 8, y = 60, z = 56$

7. $\triangle ABC \cong \triangle ADC, ASA = ASA: \angle BAC, AC, \angle ACB$$\triangle ABC = \angle DAC, AC, \angle ACD$de$\triangle ADC, x = 3, y = 4$

9. $AB = DE, BC = EF, AC = DF$dado,$\triangle ABC \cong \triangle DEF$. $SSS = SSS, \angle A = \angle D$correspondientes de$\angle$$\cong \triangle$'s son =.

11. $AB = AD, BC = DC$dado,$AC = AC$ identidad,$\triangle ABC \cong \triangle ADC$. $SSS = SSS$,$\angle BAC = \angle CAD$ los correspondientes de$\angle$$\cong \triangle$'s son =.

13. $AE = CE$dado, los$\angle AEB = \angle CED$ verticales$\angle$ son =,$EB = ED$ dado,$\triangle AEB \cong \triangle CED$$SAS = SAS$, los lados$AB = CD$ correspondientes$\cong \triangle$ de los son =.

Sección 2.7

1. (1)$\triangle ABC \cong \triangle DEF$

(2) Hyp-Leg = Hyp-Leg:$AB, BC$$\triangle ABC = DE, EF$ de$\triangle DEF$

(3)$x = 42, y = 48$

3. Los triángulos no pueden demostrarse congruentes.

5. Los triángulos no pueden demostrarse congruentes.

7. (1)$\triangle ABC \cong \triangle CDA$

(2)$AAS = AAS: \angle B, \angle BCA, CA$$\triangle ABC = \angle D, \angle DAC, AC$ de$\triangle CDA$

(3)$x = 25, y = 20$

9. (1)$\triangle ACD \cong \triangle BCD$

(2)$SAS = SAS: AD, \angle ADC, DC$$\triangle ACD = BD, \angle BDC, DC$ de$\triangle BCD$

(3)$x = 4$

11. Los triángulos no pueden demostrarse congruentes.

13. Los triángulos no pueden demostrarse congruentes.

15. Los triángulos no pueden demostrarse congruentes.

17. $OP = OP$identidad,$OA = OB$ dada,$\triangle OAP \cong \triangle OBP$ Hyp-Leg = Hyp-Leg, los lados$AP = BP$ correspondientes de$\cong \triangle$'s son =.

19. $AB = CD, AD = CB$dado,$BD = DB$ identidad,$\triangle ABD \cong \triangle CDB$$SSS = SSS, \angle A = \angle C$ correspondientes$\angle$'s de$\cong \triangle$'s son =.

21. $AD = BD$dado,$\angle ADC = \angle BDC = 90^{\circ}$ dado$AB \perp CD$,$CD = CD$ identidad,$\triangle ACD \cong \triangle BCD$. $SAS = SAS, \angle A = \angle B$correspondientes de$\angle$$\cong \triangle$'s son =.

Sección 3.1

1. $w = 40, y = 140, r = 4, s = 8$

3. $w = 35, x = 25, y = 120, z = 35$

5. $x = 130, y = 50, z = 130$

7. $x = 70, \angle A = 70^{\circ}, \angle B = 110^{\circ}, \angle C = 70^{\circ}, \angle D = 110^{\circ}$

9. $x = 25, y = 20, AC = 40, BD = 50$

11. $x = 2, AB = CD = 4$o$x = 3, AB = CD = 9$

13. $x = 4, y = 1, AB = CD = 7, AD = BC = 3$

15. $x = 4, y = 2, AC = 16, BD = 12$

17. $x = 20, y = 10, \angle A = 40^{\circ}, \angle B = 140^{\circ}, \angle C = 40^{\circ}, \angle D = 140^{\circ}$

Sección 3.2

1. $w = 50, x = 40, y = 50, z = 50$

3. $x = 30, y = 60$

5. $x = 4, y = 4, z = 4, AC = 8, BD = 8$

7. $x = 40, y = 40, z = 100$

9. 1

11. $x = y = z = 45$

13. $x = 60, y = z = 120$

15. $x = 135, y = 100$

17. $w = x = 50, y = 130, z = 50$

19. 5

Sección 4.1

1. 1

3. 12

5. 21

7. 20

9. 6

11. 1 ó 6

Sección 4.2

1. $\triangle ABC \sim \triangle FED$

3. $\triangle ABC \sim \triangle DFE$

5. $\triangle ABC \sim \triangle DBE$

7. 6

9. 7

11. 1

13. 5

15. 6

17. $x = 6, y = 1.5$

19. 15

21. $x = 4.5, y = 1.5, z = 15$

23. 100 pies

Sección 4.3

1. 5

3. 1.5

5. 4

Sección 4.4

1. 10

3. 8

5. $\sqrt{2}$

7. $\sqrt{3}$

9. $3\sqrt{2}$

11. $x = 6, BC = 6, AC = 8, AB = 10$

13. $x = 17, PR = 8, QR = 15, PQ = 17$

15. $2\sqrt{2}$

17. $x = 3, AB = 16$

19. $x = 7, AC = 30, BD = 16$

21. $x = 8, y = 6$

23. $x = 5, AB = 12, BD = 13$

25. si

27. no

29. no

31. 24 pies

33. no

Sección 4.5

1. $x = 3\sqrt{3}, y = 6$

3. $x = 5, y = 5\sqrt{3}$

5. $x = \sqrt{3}, y = 2\sqrt{3}$

7. $x = 3, y = 3\sqrt{2}$

9. $x = y = 5\sqrt{2}$

11. $10\sqrt{2}$

13. $3\sqrt{2}$

15. $x = 8, y = 4\sqrt{3}$

17. $x = y = (5\sqrt{2})/2$

19. $x = 3, y = 3\sqrt{3}$

21. $x = 5\sqrt{3}, AB = 20$

23. $x = 3, y = 6$

25. $AC = 8, BD = 8\sqrt{3}$

Sección 4.6

1. 4

3. $\sqrt{3}$

5. $2\sqrt{2}$

Sección 5.1

1. $\dfrac{12}{13}$,$\dfrac{5}{13}$,$\dfrac{12}{5}$,$\dfrac{5}{13}$,$\dfrac{12}{13}$,$\dfrac{5}{12}$

3. $\dfrac{8}{17}$,$\dfrac{15}{17}$,$\dfrac{8}{15}$,$\dfrac{15}{17}$,$\dfrac{8}{17}$,$\dfrac{15}{8}$

5. $\dfrac{1}{2}$,$\dfrac{\sqrt{3}}{2}$,$\dfrac{\sqrt{3}}{3}$,$\dfrac{\sqrt{3}}{2}$,$\dfrac{1}{2}$,$\sqrt{3}$

7. $\dfrac{\sqrt{2}}{2}$,$\dfrac{\sqrt{2}}{2}$, 1,$\dfrac{\sqrt{2}}{2}$,$\dfrac{\sqrt{2}}{2}$, 1

9. $\dfrac{\sqrt{3}}{2}$,$\dfrac{1}{2}$,$\sqrt{3}$,$\dfrac{1}{2}$,$\dfrac{\sqrt{3}}{2}$,$\dfrac{\sqrt{3}}{3}$

11. $\dfrac{2}{3}$,$\dfrac{\sqrt{5}}{3}$,$\dfrac{2\sqrt{5}}{5}$,$\dfrac{\sqrt{5}}{3}$,$\dfrac{2}{3}$,$\dfrac{\sqrt{5}}{2}$.

13. $\dfrac{1}{2}$,$\dfrac{\sqrt{3}}{2}$$\dfrac{\sqrt{3}}{3}$,$\dfrac{\sqrt{3}}{2}$,$\dfrac{1}{2}$,$\sqrt{3}$

15. $\dfrac{3}{5}$,$\dfrac{4}{3}$

17. $\dfrac{1}{2}$,$\dfrac{\sqrt{3}}{3}$

19. $\dfrac{3\sqrt{10}}{10}$,$\dfrac{\sqrt{10}}{10}$

Sección 5.2

1. .1736

3. .1736

5. 1.0000

7. .3090

9. 1.1918

11. 6.4

13. 7.7

15. 11.9

17. 8.4

19. 44.8

21. 7.8

23. 20.5

25. 14.5

27. 7.3

29. 4.8

31. $42^{\circ}$

33. $37^{\circ}$

35. $56^{\circ}$

37. $48^{\circ}$

39. 4.6

41. $x = 4.6, y = 7.7$

43. 7.8

45. $x = 8.2, y = 26.5$

Sección 5.3

1. 50.3 pies

3. 5759 pies

5. $1^{\circ}$

7. 18.8 pies

Sección 6.1

1. $A = 12, P = 16$

3. $A = 49, P = 28$

5. $A = 3, P = 4\sqrt{5}$

7. $A = 120, P = 46$

9. $A = 48, P = 28$

11. $A = 25\sqrt{3}, P = 10 + 10\sqrt{3}$

13. $A = 50, P = 20\sqrt{2}$

15. 4

17. 4

19. 48000 pies cuadrados

21. 296

23. 450

25. 1800 libras

Sección 6.2

1. $A = 240, P = 66$

3. $A = 36, P = 28$

5. $A = 96.4, P = 50$

7. $A = 10, P = 10 + 4\sqrt{2}$

9. 7

11. 4

13. $x = 8, y = 5$

Sección 6.3

1. 60

3. 10

5. 11.5

7. $A = 6, P = 12$

9. $A = 108, P = 54$

11. $A = 44, P = 28 + 4\sqrt{5}$

13. $A = 60, P = 40$

15. $A = 2, P = 4 + 2\sqrt{2}$

17. $A = 16\sqrt{3}, P = 24$

19. $A = 42.0, P = 31.4$

21. 5

23. 4

Sección 6.4

1. 42

3. $A = 96, P = 40$

5. $A = 24, P = 20$

7. $A = 32\sqrt{3}, P = 32$

9. 167.8

Sección 6.5

1. 40

3. $A = 36, P = 28$

5. $A = 32, P = 21 + \sqrt{17}$

7. $A = 44, P = 32$

9. $A = 50 + 25\sqrt{3}, P = 40 + 10\sqrt{3}$

11. $A = 375\sqrt{3}, P = 95 + 5\sqrt{21}$

13. $A = 269.2, P = 84.9$

15. 7

Sección 7.1

1. $x = y = z = 60, r = 3$

3. $x = 72, y = z = 54, r = 7$

5. $x = 90, y = z = 45, r = 5$

7. $a = 27.5, P = 200, A = 2752.8$

9. $a = 17.3, P = 120, A = 1039.2$

11. $a = 30.8, P = 200, A = 3077.7$

13. $a = 16.2, P = 117.6, A = 951.1$

15. $a = 8.7, P = 60, A = 259.8$

17. $a = 9.5, P = 61.8, A = 293.9$

Sección 7.2

1. $r = 20, d = 40$

3. 30

5. 6

7. $r = 15, d = 30$

9. $r = 10, d = 20$

11. $AB = 12, CD = 16$

Sección 7.3

1. 15

3. 80

5. $x = 40, \angle O = 125^{\circ}, \angle P = 55^{\circ}$

7. $x = 25, y = 24$

9. 10

11. 7

13. 36

15. 40

Sección 7.4

1. $\widehat{AB} \stackrel{\circ}{=} 60^{\circ}, \widehat{ACB} \stackrel{\circ}{=} 300^{\circ}$

3. $\widehat{AB} \stackrel{\circ}{=} 80^{\circ}, \widehat{ACB} \stackrel{\circ}{=} 280^{\circ}$

5. $x = 80, y = 70, z = 90$

7. $x = 60, y = 60, z = 60$

9. $x = 35, y = 70, z = 70$

11. 130

13. 50

15. 60

17. 70

19. 50

21. 90

23. 12

25. 40

27. $x = 50, y = z = 25$

29. 70

31. $x = 45, y = 45, z = 90$

33. 35

35. $x =. 70, y = 40, z = 30$

37. 80

39. $x = 45, y = 15, z = 60$

41. $x = 30, y = 50, z = 80$

43. 30

45. 70

Sección 7.5

1. 31.4

3. 62.8

5. 12.56, 25.12

7. 40.82

9. 8.37

11. 52.3

13. 6.28

15. $\widehat{AB} = 3.925, \widehat{CD} = 7.85$

17. 39.1

19. 94.2

21. 62.8

23. $r = 50, d = 100$

25. 43.96 pulgadas

27. 7907.6 millas

Sección 7.6

1. 3.14

3. 12.56

5. 78.5

7. 1256

9. 113.04

11. 157

13. 62.8

15. $(200\pi/3) - 100\sqrt{3}$

17. $25\pi - 50$

19. $100\pi - 200$

21. $100 - 25\pi$

23. $200 + 25\pi$

25. $21 \pi$

27. $50\pi$

29. $100 - 25\pi$