3.1E: Ejercicios para la Sección 3.1

Para los ejercicios 1 - 10, usa la ecuación\( m_{\text{sec}}=\dfrac{f(x)−f(a)}{x−a} \) para encontrar la pendiente de la línea secante entre los valores\(x_1\) y\(x_2\) para cada función\(y=f(x)\).

1)\(f(x)=4x+7; \quad x_1=2, \quad x_2=5\)

Contestar

\(m_{\text{sec}}=4\)

2)\(f(x)=8x−3;\quad x_1=−1,\quad x_2=3\)

3)\(f(x)=x^2+2x+1;\quad x_1=3,\quad x_2=3.5\)

Contestar

\(m_{\text{sec}}=8.5\)

4)\(f(x)=−x^2+x+2;\quad x_1=0.5,\quad x_2=1.5\)

5)\(f(x)=\dfrac{4}{3x−1};\quad x_1=1,\quad x_2=3\)

Contestar

\(m_{\text{sec}}=−\frac{3}{4}\)

6)\(f(x)=\dfrac{x−7}{2x+1};\quad x_1=−2,\quad x_2=0\)

7)\(f(x)=\sqrt{x};\quad x_1=1,\quad x_2=16\)

Contestar

\(m_{\text{sec}}=0.2\)

8)\(f(x)=\sqrt{x−9};\quad x_1=10,\quad x_2=13\)

9)\(f(x)=x^{1/3}+1;\quad x_1=0,\quad x_2=8\)

Contestar

\(m_{\text{sec}}=0.25\)

10)\(f(x)=6x^{2/3}+2x^{1/3};\quad x_1=1,\quad x_2=27\)

Para las funciones en los ejercicios 11 a 20,

a. utilice la ecuación\( \displaystyle m_{\text{tan}}=\lim_{h→0}\frac{f(a+h)−f(a)}{h} \) para encontrar la pendiente de la línea tangente\(m_{\text{tan}}=f′(a)\), y

b. encontrar la ecuación de la línea tangente a\(f\) at\(x=a\).

11)\(f(x)=3−4x, \quad a=2\)

Contestar

a.\(m_{\text{tan}}=−4\)
b.\(y=−4x+3\)

12)\(f(x)=\dfrac{x}{5}+6, \quad a=−1\)

13)\(f(x)=x^2+x, \quad a=1\)

Contestar

a.\(m_{\text{tan}}=3\)
b.\(y=3x−1\)

14)\(f(x)=1−x−x^2, \quad a=0\)

15)\(f(x)=\dfrac{7}{x}, \quad a=3\)

Contestar

a.\(m_{\text{tan}}=\frac{−7}{9}\)
b.\(y=\frac{−7}{9}x+\frac{14}{3}\)

16)\(f(x)=\sqrt{x+8}, \quad a=1\)

17)\(f(x)=2−3x^2, \quad a=−2\)

Contestar

a.\(m_{\text{tan}}=12\)
b.\(y=12x+14\)

18)\(f(x)=\dfrac{−3}{x−1}, \quad a=4\)

19)\(f(x)=\dfrac{2}{x+3}, \quad a=−4\)

Contestar

a.\(m_{\text{tan}}=−2\)
b.\(y=−2x−10\)

20)\(f(x)=\dfrac{3}{x^2}, \quad a=3\)

Para las funciones\(y=f(x)\) en los ejercicios 21 - 30, encuentra\(f′(a)\) usando la ecuación\( \displaystyle f′(a)=\lim_{x→a}\frac{f(x)−f(a)}{x−a} \).

21)\(f(x)=5x+4, \quad a=−1\)

Contestar

\(f'(-1) = 5\)

22)\(f(x)=−7x+1, \quad a=3\)

23)\(f(x)=x^2+9x, \quad a=2\)

Contestar

\(f'(2) = 13\)

24)\(f(x)=3x^2−x+2, \quad a=1\)

25)\(f(x)=\sqrt{x}, \quad a=4\)

Contestar

\(f'(4) = \frac{1}{4}\)

26)\(f(x)=\sqrt{x−2}, \quad a=6\)

27)\(f(x)=\dfrac{1}{x}, \quad a=2\)

Contestar

\(f'(2) = −\frac{1}{4}\)

28)\(f(x)=\dfrac{1}{x−3}, \quad a=−1\)

29)\(f(x)=\dfrac{1}{x^3}, \quad a=1\)

Contestar

\(f'(1) = -3\)

30)\(f(x)=\dfrac{1}{\sqrt{x}}, \quad a=4\)

Para los siguientes ejercicios, dada la función\(y=f(x)\),

a. encontrar la pendiente de la línea secante\(PQ\) para cada punto\(Q(x,f(x))\) con el\(x\) valor dado en la tabla.

b. Utilice las respuestas de a. para estimar el valor de la pendiente de la línea tangente en\(P\).

c. Usa la respuesta de b. para encontrar la ecuación de la línea tangente\(f\) a punto\(P\).

31) [T]\(f(x)=x^2+3x+4, \quad P(1,8)\) (Redondear a\(6\) decimales.)

\(x\)	\(Slope m_{PQ}\)	\(x\)	\(Slope m_{PQ}\)
1.1	(i)	0.9	vii)
1.01	ii)	0.99	viii)
1.001	iii)	0.999	ix)
1.0001	iv)	0.9999	(x)
1.00001	(v)	0.99999	(xi)
1.000001	vi)	0.999999	(xii)

Contestar

\(a. (i)5.100000, (ii)5.010000, (iii)5.001000, (iv)5.000100, (v)5.000010, (vi)5.000001, (vii)4.900000, (viii)4.990000, (ix)4.999000, (x)4.999900, (xi)4.999990, (x)4.999999\)
b.\(m_{\text{tan}}=5\)
c.\(y=5x+3\)

32) [T]\(f(x)=\dfrac{x+1}{x^2−1}, \quad P(0,−1)\)

\(x\)	\(Slope m_{PQ}\)	\(x\)	\(Slope m_{PQ}\)
0.1	(i)	−0.1	vii)
0.01	ii)	−0.01	viii)
0.001	iii)	−0.001	ix)
0.0001	iv)	−0.0001	(x)
0.00001	(v)	−0.00001	(xi)
0.000001	vi)	−0.000001	(xii)

33) [T]\(f(x)=10e^{0.5x}, \quad P(0,10)\) (Redondear a\(4\) decimales.)

\(x\)	\(Slope m_{PQ}\)
−0.1	(i)
−0.01	ii)
−0.001	iii)
−0.0001	iv)
−0.00001	(v)
−0.000001	vi)

Contestar

a.\((i)4.8771, \;(ii)4.9875, \;(iii)4.9988, \;(iv)4.9999, \;(v)4.9999, \;(vi)4.9999 \)
b.\(m_{\text{tan}}=5\)
c.\(y=5x+10\)

34) [T]\(f(x)=\tan(x), \quad P(π,0)\)

\(x\)	\(Slope m_{PQ}\)
3.1	(i)
3.14	ii)
3.141	iii)
3.1415	iv)
3.14159	(v)
3.141592	vi)

[T] Para las siguientes funciones de posición\(y=s(t)\), un objeto se mueve a lo largo de una línea recta, donde\(t\) está en segundos y\(s\) está en metros. Encuentra

a. la expresión simplificada para la velocidad promedio de\(t=2\) a\(t=2+h\);

b. la velocidad promedio entre\(t=2\) y\(t=2+h\), donde\((i)\;h=0.1, \;(ii)\;h=0.01, \;(iii)\;h=0.001\), y\((iv)\;h=0.0001\); y

c. utilizar la respuesta de a. para estimar la velocidad instantánea en\(t=2\) segundo lugar.

35)\(s(t)=\frac{1}{3}t+5\)

Contestar

a.\(\frac{1}{3}\);
b.\((i)\;\frac{1}{3}\) m/s,\((ii)\;\frac{1}{3}\) m/s,\((iii)\;\frac{1}{3}\) m/s,\((iv)\;\frac{1}{3}\) m/s;
c.\(\frac{1}{3}\) m/s

36)\(s(t)=t^2−2t\)

37)\(s(t)=2t^3+3\)

Contestar

a.\(2(h^2+6h+12)\);
b.\((i)\;25.22\) m/s,\((ii)\; 24.12\) m/s,\((iii)\; 24.01\) m/s,\((iv)\; 24\) m/s;
c.\(24\) m/s

38)\(s(t)=\dfrac{16}{t^2}−\dfrac{4}{t}\)

39) Utilice la siguiente gráfica para evaluar a.\(f′(1)\) y b.\(f′(6).\)

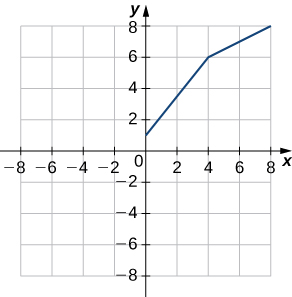
Contestar

a.\(1.25\); b.\(0.5\)

40) Utilice la siguiente gráfica para evaluar a.\(f′(−3)\) y b\(f′(1.5)\).

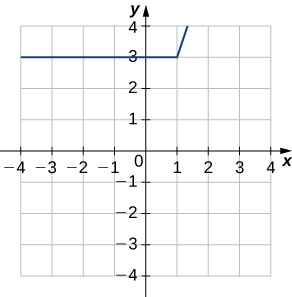
Para los siguientes ejercicios, utilice la definición límite de derivada para demostrar que la derivada no existe en\(x=a\) para cada una de las funciones dadas.

41)\(f(x)=x^{1/3}, \quad x=0\)

Contestar

\(\displaystyle \lim_{x→0^−}\frac{x^{1/3}−0}{x−0}=\lim_{x→0^−}\frac{1}{x^{2/3}}=∞\)

42)\(f(x)=x^{2/3}, \quad x=0\)

43)\(f(x)=\begin{cases}1, & \text{if } x<1\\x, & \text{if } x≥1\end{cases}, \quad x=1\)

Contestar

\(\displaystyle \lim_{x→1^−}\frac{1−1}{x−1}=0≠1=\lim_{x→1^+}\frac{x−1}{x−1}\)

44)\(f(x)=\dfrac{|x|}{x}, \quad x=0\)

45) [T] La posición en pies de un auto de carreras a lo largo de una pista recta después de\(t\) segundos es modelada por la función\(s(t)=8t^2−\frac{1}{16}t^3.\)

a. Encuentre la velocidad promedio del vehículo en los siguientes intervalos de tiempo a cuatro decimales:

i. [\(4, 4.1\)]

ii. [\(4, 4.01\)]

iii. [\(4, 4.001\)]

iv. [\(4, 4.0001\)]

b. Utilice a. para sacar una conclusión sobre la velocidad instantánea del vehículo a los\(t=4\) segundos.

Contestar

a.\((i)61.7244 ft/s, \;(ii)61.0725 ft/s, \;(iii)61.0072 ft/s, \;(iv)61.0007 ft/s\)
b. A los\(4\) segundos el auto de carreras viaja a una velocidad/velocidad de\(61\) pies/s.

46) [T] La distancia en pies que una bola rueda por una pendiente es modelada por la función\(s(t)=14t^2\),

donde t es segundos después de que la pelota comience a rodar.

a. Encuentra la velocidad promedio de la pelota en los siguientes intervalos de tiempo:

i. [5, 5.1]

ii. [5, 5.01]

iii. [5, 5.001]

iv. [5, 5.0001]

b. Usa las respuestas de a. para sacar una conclusión sobre la velocidad instantánea de la pelota a los\(t=5\) segundos.

47) Dos vehículos empiezan viajando uno al lado del otro por una carretera recta. Sus funciones de posición, mostradas en la siguiente gráfica, están dadas por\(s=f(t)\) y\(s=g(t)\), donde s se mide en pies y t se mide en segundos.

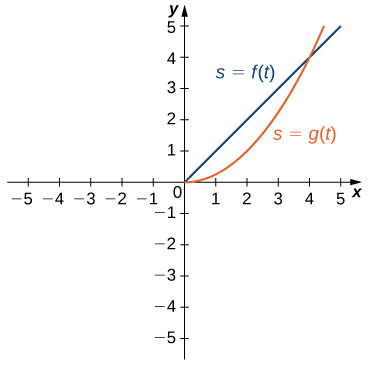
a. ¿Qué vehículo ha viajado más lejos en\(t=2\) segundos?

b. ¿Cuál es la velocidad aproximada de cada vehículo en\(t=3\) segundos?

c. ¿Qué vehículo viaja más rápido en\(t=4\) segundos?

d. ¿Qué es cierto acerca de las posiciones de los vehículos a los\(t=4\) segundos?

Contestar

a.- El vehículo representado por\(f(t)\), porque ha recorrido\(2\) pies, mientras que\(g(t)\) ha recorrido\(1\) pie.
b. La velocidad de\(f(t)\) es constante a\(1\) pies/s, mientras que la velocidad de\(g(t)\) es aproximadamente\(2\) ft/s.
c. El vehículo representado por\(g(t)\), con una velocidad de aproximadamente\(4\) pies/s.
d. Ambos han viajado \(4\)pies en\(4\) segundos.

48) [T] El costo total\(C(x)\), en cientos de dólares, para producir\(x\) tarros de mayonesa viene dado por\(C(x)=0.000003x^3+4x+300\).

a. Calcule el costo promedio por frasco en los siguientes intervalos:

i. [100, 100.1]

ii. [100, 100.01]

iii. [100, 100.001]

iv. [100, 100.0001]

b. utilizar las respuestas de a. para estimar el costo promedio para producir\(100\) tarros de mayonesa.

49) [T] Para la función\(f(x)=x^3−2x^2−11x+12\), haga lo siguiente.

a. Utilice una calculadora gráfica para graficar\(f\) en una ventana de visualización apropiada.

b. Utilice la función ZOOM en la calculadora para aproximar los dos valores\(x=a\) para los cuales\(m_{tan}=f′(a)=0\).

Contestar

a.

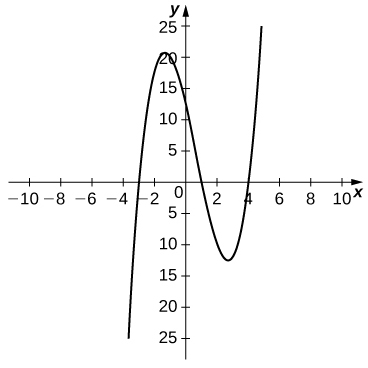
b.\(a≈−1.361,\;2.694\)

50) [T] Para la función\(f(x)=\dfrac{x}{1+x^2}\), haga lo siguiente.

a. Utilice una calculadora gráfica para graficar\(f\) en una ventana de visualización apropiada.

b. Utilice la función ZOOM en la calculadora para aproximar los valores de\(x=a\) los cuales\(m_{\text{tan}}=f′(a)=0\).

51) Supongamos que\(N(x)\) calcula el número de galones de gas utilizados por un vehículo que recorre\(x\) millas. Supongamos que el vehículo recibe\(30\) mpg.

a. Encontrar una expresión matemática para\(N(x)\).

b. ¿Qué es\(N(100)\)? Explicar el significado físico.

c. ¿Qué es\(N′(100)\)? Explicar el significado físico.

Contestar

a.\(N(x)=\dfrac{x}{30}\)
b. ∼\(3.3\) galones. Cuando el vehículo recorre\(100\) millas, ha utilizado\(3.3\) galones de gas.
\(\frac{1}{30}\)c. La tasa de consumo de gas en galones por milla que el vehículo está logrando después de haber recorrido\(100\) millas.

52) [T] Para la función\(f(x)=x^4−5x^2+4\), haga lo siguiente.

a. Utilice una calculadora gráfica para graficar\(f\) en una ventana de visualización apropiada.

b. utilizar la\(nDeriv\) función, que encuentra numéricamente la derivada, en una calculadora gráfica para estimar\(f′(−2),\;f′(−0.5),\;f′(1.7)\), y\(f′(2.718)\).

53) [T] Para la función\(f(x)=\dfrac{x^2}{x^2+1}\), haga lo siguiente.

a. Utilice una calculadora gráfica para graficar\(f\) en una ventana de visualización apropiada.

b. Utilice la\(nDeriv\) función en una calculadora gráfica para encontrar\(f′(−4),\;f′(−2),\;f′(2)\), y\(f′(4)\).

Contestar

a.

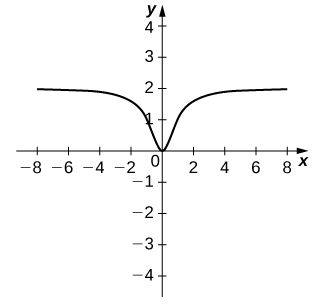
b.\(−0.028,−0.16,0.16,0.028\)