9.4: Pruebas de comparación

Objetivos de aprendizaje

• Utilice la prueba de comparación para probar una serie para la convergencia.
• Utilice la prueba de comparación de límites para determinar la convergencia de una serie.

Hemos visto que la prueba integral nos permite determinar la convergencia o divergencia de una serie comparándola con una integral impropia relacionada. En esta sección, se muestra cómo utilizar pruebas de comparación para determinar la convergencia o divergencia de una serie comparándola con una serie cuya convergencia o divergencia es conocida. Normalmente estas pruebas se utilizan para determinar la convergencia de series que son similares a series geométricas o\(p\) series.

Prueba de comparación

En las dos secciones anteriores, se discutieron dos grandes clases de series: series geométricas y\(p\) -series. Sabemos exactamente cuándo convergen estas series y cuándo divergen. Aquí mostramos cómo usar la convergencia o divergencia de estas series para probar convergencia o divergencia para otras series, utilizando un método llamado prueba de comparación.

Por ejemplo, considere la serie

\[\sum_{n=1}^∞\dfrac{1}{n^2+1}. \nonumber \]

Esta serie se parece a la serie convergente

\[\sum_{n=1}^∞\dfrac{1}{n^2} \nonumber \]

Dado que los términos en cada una de las series son positivos, la secuencia de sumas parciales para cada serie es monótona creciente. Además, desde

\[0<\dfrac{1}{n^2+1}<\dfrac{1}{n^2} \nonumber \]

para todos los enteros positivos\(n\), la suma\(k^{\text{th}}\) parcial\(S_k\) de\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^2+1}\) satisface

\[S_k=\sum_{n=1}^k\dfrac{1}{n^2+1}<\sum_{n=1}^k\dfrac{1}{n^2}<\sum_{n=1}^∞\dfrac{1}{n^2}. \nonumber \]

(Ver Figura\(\PageIndex{1a}\) y Tabla\(\PageIndex{1}\).) Dado que la serie de la derecha converge, la secuencia\({S_k}\) está delimitada arriba. Concluimos que\({S_k}\) es una secuencia monótona creciente que está delimitada arriba. Por tanto, por el Teorema de Convergencia Monótona,\({S_k}\) converge, y así

\[\sum_{n=1}^∞\dfrac{1}{n^2+1} \nonumber \]

converge.

Del mismo modo, considere la serie

\[\sum_{n=1}^∞\dfrac{1}{n−1/2}. \nonumber \]

Esta serie se parece a la serie divergente

\[\sum_{n=1}^∞\dfrac{1}{n}. \nonumber \]

La secuencia de sumas parciales para cada serie es monótona creciente y

\[\dfrac{1}{n−1/2}>\dfrac{1}{n}>0 \nonumber \]

por cada entero positivo\(n\). Por lo tanto, la suma\(k^{\text{th}}\) parcial\(S_k\) de

\[ \sum^∞_{n=1}\dfrac{1}{n−1/2} \nonumber \]

satisface

\[S_k=\sum_{n=1}^k\dfrac{1}{n−1/2}>\sum_{n=1}^k\dfrac{1}{n}. \nonumber \]

(Ver Figura\(\PageIndex{1n}\) y Tabla\(\PageIndex{1}\)). Dado que la serie\(\displaystyle \sum^∞_{n=1}\frac{1}{n}\) diverge hasta el infinito, la secuencia de sumas parciales no\(\displaystyle \sum^k_{n=1}\frac{1}{n}\) tiene límites. En consecuencia,\({S_k}\) es una secuencia no acotada, y por lo tanto diverge. Concluimos que

\[\sum_{n=1}^∞\dfrac{1}{n−1/2} \nonumber \]

diverge.

Figura\(\PageIndex{1}\): (a) Cada una de las sumas parciales para la serie dada es menor que la suma parcial correspondiente para la convergente\(p−series\). (b) Cada una de las sumas parciales para la serie dada es mayor que la suma parcial correspondiente para la serie armónica divergente.

Tabla\(\PageIndex{1}\): Comparando una serie con a\(p\) -series (\(p = 2\))

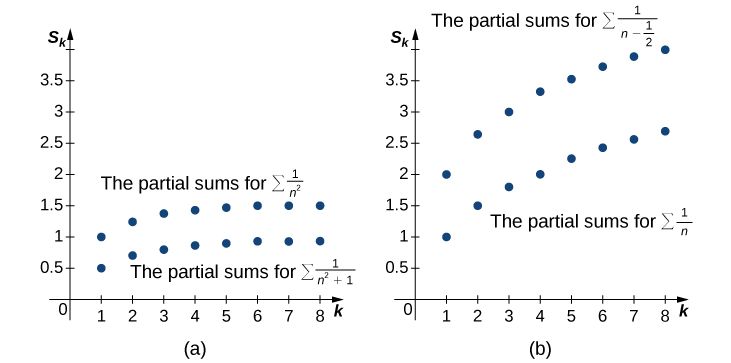
\(k\)	1	2	3	4	5	6	7	8
\(\displaystyle \sum_{n=1}^k\dfrac{1}{n^2+1}\)	0.5	0.7	0.8	0.8588	0.8973	0.9243	0.9443	0.9597
\(\displaystyle \sum_{n=1}^k\dfrac{1}{n^2}\)	1	1.25	1.3611	1.4236	1.4636	1.4914	1.5118	1.5274

Tabla\(\PageIndex{2}\): Comparando una serie con la serie armónica

\(k\)	1	2	3	4	5	6	7	8
\(\displaystyle \sum_{n=1}^k\dfrac{1}{n−1/2}\)	2	2.6667	3.0667	3.3524	3.5746	3.7564	3.9103	4.0436
\(\displaystyle \sum_{n=1}^k\dfrac{1}{n}\)	1	1.5	1.8333	2.0933	2.2833	2.45	2.5929	2.7179

Prueba de comparación

1. Supongamos que existe un entero\(N\) such that \(0≤a_n≤b_n\) for all \(n≥N\). If \(\displaystyle \sum^∞_{n=1}b_n\) converges, then \(\displaystyle \sum^∞_{n=1}a_n\) converges.
2. Supongamos que existe un entero\(N\) such that \(a_n≥b_n≥0\) for all \(n≥N.\) If \(\displaystyle \sum^∞_{n=1}b_n\) diverges, then \(\displaystyle \sum^∞_{n=1}a_n\) diverges.

Prueba

Demostramos la parte i. La prueba de la parte ii. es la contrapositiva de la parte i.\({S_k}\) be the sequence of partial sums associated with \(\displaystyle \sum^∞_{n=1}a_n\), and let \(\displaystyle L=\sum^∞_{n=1}b_n\). Since the terms \(a_n≥0,\)

\[S_k=a_1+a_2+⋯+a_k≤a_1+a_2+⋯+a_k+a_{k+1}=S_{k+1}. \nonumber \]

Por lo tanto, la secuencia de sumas parciales va en aumento. Además, desde\(a_n≤b_n\) for all \(n≥N\), then

\[\sum_{n=N}^ka_n≤\sum_{n=N}^kb_n≤\sum_{n=1}^∞b_n=L. \nonumber \]

Por lo tanto, para todos\(k≥1\),

\[S_k=(a_1+a_2+⋯+a_{N−1})+\sum_{n=N}^ka_n≤(a_1+a_2+⋯+a_{N−1})+L. \nonumber \]

Desde\(a_1+a_2+⋯+a_{N−1}\) is a finite number, we conclude that the sequence \({S_k}\) is bounded above. Therefore, \({S_k}\) is an increasing sequence that is bounded above. By the Monotone Convergence Theorem, we conclude that \({S_k}\) converges, and therefore the series \(\displaystyle \sum_{n=1}^∞a_n\) converges.

□

Utilizar la prueba de comparación para determinar la convergencia o divergencia de una serie\(\displaystyle \sum_{n=1}^∞a_n\), it is necessary to find a suitable series with which to compare it. Since we know the convergence properties of geometric series and \(p\)-series, these series are often used. If there exists an integer \(N\) such that for all \(n≥N\), each term an is less than each corresponding term of a known convergent series, then \(\displaystyle \sum_{n=1}^∞a_n\) converges. Similarly, if there exists an integer \(N\) such that for all \(n≥N\), each term an is greater than each corresponding term of a known divergent series, then \(\displaystyle \sum_{n=1}^∞a_n\) diverges.

Ejemplo\(\PageIndex{1}\): Using the Comparison Test

Para cada una de las siguientes series, utilice la prueba de comparación para determinar si la serie converge o diverge.

1. \(\displaystyle \sum_{n=1}^∞=\dfrac{1}{n^3+3n+1}\)
2. \(\displaystyle \sum_{n=1}^∞=\dfrac{1}{2^n+1}\)
3. \(\displaystyle \sum_{n=2}^∞=\dfrac{1}{\ln \,n }\)

Solución

a. Comparar con\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3}\). Ya que\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3}\) es una\(p\) -serie con\(p=3\), converge. Además,

\[\dfrac{1}{n^3+3n+1}<\dfrac{1}{n^3} \nonumber \]

por cada entero positivo\(n\). Por lo tanto, podemos concluir que\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^3+3n+1}\) converge.

b. comparar con\(\displaystyle \sum^∞_{n=1}\left(\dfrac{1}{2}\right)^n\). Ya que\(\displaystyle \sum_{n=1}^∞\left(\dfrac{1}{2}\right)^n\) es una serie geométrica con\(r=\dfrac{1}{2}\) y\(\left|\dfrac{1}{2}\right|<1\), converge. Además,

\[\dfrac{1}{2^n+1}<\dfrac{1}{2^n} \nonumber \]

por cada entero positivo\(n\). Por lo tanto, vemos que\(\displaystyle \sum^∞_{n=1}\dfrac{1}{2^n+1}\) converge.

c. Comparar con\(\displaystyle \sum^∞_{n=2}\dfrac{1}{n}\). Desde

\[\dfrac{1}{\ln n }>\dfrac{1}{n} \nonumber \]

por cada entero\(n≥2\) y\(\displaystyle \sum^∞_{n=2}\dfrac{1}{n}\) diverge, tenemos que\(\displaystyle \sum^∞_{n=2}\dfrac{1}{\ln n}\) diverge.

Ejercicio\(\PageIndex{1}\)

Utilice la prueba de comparación para determinar si la serie\(\displaystyle \sum^∞_{n=1}\dfrac{n}{n^3+n+1}\) converge o diverge.

Pista

Encuentra un valor\(p\) tal que\(\dfrac{n}{n^3+n+1}≤\dfrac{1}{n^p}\).

Responder

La serie converge.

Prueba de comparación de límites

La prueba de comparación funciona bien si podemos encontrar una serie comparable que satisfaga la hipótesis de la prueba. Sin embargo, a veces encontrar una serie apropiada puede ser difícil. Considera la serie

\[\sum_{n=2}^∞\dfrac{1}{n^2−1}. \nonumber \]

Es natural comparar esta serie con la serie convergente

\[\sum_{n=2}^∞\dfrac{1}{n^2}. \nonumber \]

Sin embargo, esta serie no satisface la hipótesis necesaria para utilizar la prueba de comparación porque

\[\dfrac{1}{n^2−1}>\dfrac{1}{n^2} \nonumber \]

para todos los enteros\(n≥2\). Aunque podríamos buscar una serie diferente con la que comparar\(\displaystyle \sum^∞_{n=2}\frac{1}{n^2−1},\) en su lugar mostramos cómo podemos usar la prueba de comparación de límites para comparar

\[\sum_{n=2}^∞\frac{1}{n^2−1} \nonumber \]

y

\[\sum_{n=2}^∞\frac{1}{n^2}. \nonumber \]

Examinemos la idea detrás de la prueba de comparación de límites. Considerar dos series\(\displaystyle \sum^∞_{n=1}a_n\) y\(\displaystyle \sum^∞_{n=1}b_n\). con términos positivos\(a_n\) y\(b_n\) y evaluar

\[\lim_{n→∞}\frac{a_n}{b_n}. \nonumber \]

Si

\[\lim_{n→∞}\frac{a_n}{b_n}=L≠0, \nonumber \]

entonces, para\(n\) suficientemente grande,\(a_n≈Lb_n\). Por lo tanto, ambas series convergen o ambas series divergen. Para la serie\(\displaystyle \sum^∞_{n=2}\frac{1}{n^2−1}\) y\(\displaystyle \sum^∞_{n=2}\dfrac{1}{n^2}\), vemos que

\[\lim_{n→∞}\dfrac{1/(n^2−1)}{1/n^2}=\lim_{n→∞}\dfrac{n^2}{n^2−1}=1. \nonumber \]

Dado que\(\displaystyle \sum^∞_{n=2}\frac{1}{n^2}\) converge, concluimos que

\[\sum_{n=2}^∞\dfrac{1}{n^2−1} \nonumber \]

converge.

La prueba de comparación de límites se puede utilizar en otros dos casos. Supongamos

\[\lim_{n→∞}\dfrac{a_n}{b_n}=0. \nonumber \]

En este caso,\({a_n/b_n}\) es una secuencia acotada. En consecuencia, existe una constante\(M\) tal que\(a_n≤Mb_n\). Por lo tanto, si\(\displaystyle \sum^∞_{n=1}b_n\) converge, entonces\(\displaystyle \sum^∞_{n=1}a_n\) converge. Por otro lado, supongamos

\[\lim_{n→∞}\dfrac{a_n}{b_n}=∞. \nonumber \]

En este caso,\({a_n/b_n}\) es una secuencia sin límites. Por lo tanto, por cada constante\(M\) existe un entero\(N\) tal que\(a_n≥Mb_n\) para todos\(n≥N.\) Por lo tanto, si\(\displaystyle \sum^∞_{n=1}b_n\) diverge, entonces\(\displaystyle \sum^∞_{n=1}a_n\) diverge también.

Prueba de comparación de límites

Dejar\(a_n,b_n≥0\) para todos\(n≥1.\)

1. Si\(\displaystyle \lim_{n→∞}\frac{a_n}{b_n}=L≠0,\) entonces\(\displaystyle \sum^∞_{n=1}a_n\) y\(\displaystyle \sum^∞_{n=1}b_n\) ambos convergen o ambos divergen.
2. Si\(\displaystyle \lim_{n→∞}\frac{a_n}{b_n}=0\) y\(\displaystyle \sum^∞_{n=1}b_n\) converge, entonces\(\displaystyle \sum^∞_{n=1}a_n\) converge.
3. Si\(\displaystyle \lim_{n→∞}\frac{a_n}{b_n}=∞\) y\(\displaystyle \sum^∞_{n=1}b_n\) diverge, entonces\(\displaystyle \sum^∞_{n=1}a_n\) diverge.

Tenga en cuenta que si\(\dfrac{a_n}{b_n}→0\) y\(\displaystyle \sum^∞_{n=1}b_n\) diverge, la prueba de comparación de límites no da información. De igual manera, si\(\dfrac{a_n}{b_n}→∞\) y\(\displaystyle \sum^∞_{n=1}b_n\) converge, la prueba tampoco proporciona información. Por ejemplo, considere las dos series\(\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt{n}}\) y\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\). Estas series son ambas\(p\) -series con\(p=\frac{1}{2}\) y\(p=2\), respectivamente. Dado que\(p=\frac{1}{2}<1,\) la serie\(\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt{n}}\) diverge. Por otro lado, ya que\(p=2>1\), la serie\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\) converge. Sin embargo, supongamos que intentamos aplicar la prueba de comparación límite, usando la \(p\)serie −convergente\(\displaystyle \sum_{n=1}^∞\frac{1}{n^3}\) como nuestra serie de comparación. Primero, vemos que

\[\dfrac{1/\sqrt{n}}{1/n^3}=\dfrac{n^3}{\sqrt{n}}=n^{5/2}→∞\; \text{ as } \;n→∞. \nonumber \]

Del mismo modo, vemos que

\[\dfrac{1/n^2}{1/n^3}=n→∞\; \text{ as } \;n→∞. \nonumber \]

Por lo tanto, si\(\dfrac{a_n}{b_n}→∞\) cuando\(\displaystyle \sum_{n=1}^∞b_n\) converge, no obtenemos ninguna información sobre la convergencia o divergencia de\(\displaystyle \sum_{n=1}^∞a_n\).

Ejemplo\(\PageIndex{2}\): Using the Limit Comparison Test

Para cada una de las siguientes series, utilice la prueba de comparación de límites para determinar si la serie converge o diverge. Si la prueba no aplica, díganlo.

1. \(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}+1}\)
2. \(\displaystyle \sum^∞_{n=1}\dfrac{2^n+1}{3^n}\)
3. \(\displaystyle \sum^∞_{n=1}\dfrac{\ln(n)}{n^2}\)

Solución

a. comparar esta serie con\(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}}\). Calcular

\(\displaystyle \lim_{n→∞}\dfrac{1/(\sqrt{n}+1)}{1/\sqrt{n}}=\lim_{n→∞}\dfrac{\sqrt{n}}{\sqrt{n}+1}=\lim_{n→∞}\dfrac{1/\sqrt{n}}{1+1/\sqrt{n}}=1.\)

Por la prueba de comparación límite, ya que\(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}}\) diverge, luego\(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}+1}\) diverge.

b. comparar esta serie con\(\displaystyle \sum^∞_{n=1}\left(\dfrac{2}{3}\right)^n\). Vemos que

\(\displaystyle \lim_{n→∞}\dfrac{(2^n+1)/3^n}{2^n/3^n}=\lim_{n→∞}\dfrac{2^n+1}{3^n}⋅\dfrac{3^n}{2^n}=\lim_{n→∞}\dfrac{2^n+1}{2^n}=\lim_{n→∞}\left[1+\left(\tfrac{1}{2}\right)^n\right]=1.\)

Por lo tanto,

\(\displaystyle \lim_{n→∞}\dfrac{(2^n+1)/3^n}{2^n/3^n}=1.\)

Ya que\(\displaystyle \sum^∞_{n=1}\left(\dfrac{2}{3}\right)^n\) converge, concluimos que\(\displaystyle \sum^∞_{n=1}\dfrac{2^n+1}{3^n}\) converge.

c. Desde\(\ln n<n,\) comparar con\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n}\). Vemos que

\(\displaystyle \lim_{n→∞}\dfrac{\ln n/n^2}{1/n}=\lim_{n→∞}\dfrac{\ln n}{n^2}⋅\dfrac{n}{1}=\lim_{n→∞}\dfrac{\ln n}{n}.\)

Para evaluar\(\displaystyle \lim_{n→∞}\ln n/n\), evaluar el límite a partir\(x→∞\) de la función de valor real\(\ln(x)/x\). Estos dos límites son iguales, y hacer este cambio nos permite usar la regla de L'Hôpital. Obtenemos

\(\displaystyle \lim_{x→∞}\dfrac{lnx}{x}=\lim_{x→∞}\dfrac{1}{x}=0.\)

Por lo tanto\(\displaystyle \lim_{n→∞}\frac{\ln n}{n}=0\), y, en consecuencia,

\(\displaystyle \lim_{n→∞}\dfrac{(\ln n)/n^2}{1/n}=0.\)

Dado que el límite es\(0\) pero\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n}\) diverge, la prueba de comparación de límites no proporciona ninguna información.

Comparar con\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^2}\) en su lugar. En este caso,

\(\displaystyle \lim_{n→∞}\dfrac{(\ln n)/n^2}{1/n^2}=\lim_{n→∞}\dfrac{\ln n}{n^2}⋅\dfrac{n^2}{1}=\lim_{n→∞}\ln n=∞.\)

Dado que el límite es\(∞\) pero\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^2}\) converge, la prueba aún no proporciona ninguna información.

Entonces ahora probamos una serie entre los dos que ya probamos. Al elegir la serie\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^{3/2}}\), vemos que

\(\displaystyle \lim_{n→∞}\dfrac{(\ln n)/n^2}{1/n^{3/2}}=\lim_{n→∞}\dfrac{\ln n}{n^2}⋅\dfrac{n^{3/2}}{1}=\lim_{n→∞}\dfrac{\ln n}{\sqrt{n}}\).

Como anteriormente, para evaluar\(\displaystyle \lim_{n→∞}\frac{\ln n}{\sqrt{n}}\), evaluar el límite a partir\(x→∞\) de la función de valor real\(\frac{\ln n}{\sqrt{n}}\). Usando la regla de L'Hôpital,

\(\displaystyle \lim_{x→∞}\dfrac{\ln x}{\sqrt{x}}=\lim_{x→∞}\dfrac{2\sqrt{x}}{x}=\lim_{x→∞}\dfrac{2}{\sqrt{x}}=0\).

Dado que el límite es\(0\) y\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^{3/2}}\) converge, podemos concluir que\(\displaystyle \sum^∞_{n=1}\dfrac{\ln n}{n^2}\) converge.

Ejercicio\(\PageIndex{2}\)

Utilice la prueba de comparación de límites para determinar si la serie\(\displaystyle \sum^∞_{n=1}\dfrac{5^n}{3^n+2}\) converge o diverge.

Pista

Comparar con una serie geométrica.

Responder

La serie diverge.

Conceptos clave

• Las pruebas de comparación se utilizan para determinar la convergencia o divergencia de series con términos positivos.
• Cuando se utilizan las pruebas de comparación, a menudo\(\displaystyle \sum^∞_{n=1}a_n\) se compara una serie con una serie geométrica o\(p\) -serie.

Glosario

prueba de comparación

Si\(0≤a_n≤b_n\) para todos\(n≥N\) y\(\displaystyle \sum^∞_{n=1}b_n\) converge, entonces\(\displaystyle \sum^∞_{n=1}a_n\) converge; si\(a_n≥b_n≥0\) para todos\(n≥N\) y\(\displaystyle \sum^∞_{n=1}b_n\) diverge, entonces\(\displaystyle \sum^∞_{n=1}a_n\) diverge.

prueba de comparación de límites

Supongamos\(a_n,b_n≥0\) para todos\(n≥1\). Si\(\displaystyle \lim_{n→∞}a_n/b_n→L≠0\), entonces\(\displaystyle \sum^∞_{n=1}a_n\) y\(\displaystyle \sum^∞_{n=1}b_n\) ambos convergen o ambos divergen; si\(\displaystyle \lim_{n→∞}a_n/b_n→0\) y\(\displaystyle \sum^∞_{n=1}b_n\) converge, entonces\(\displaystyle \sum^∞_{n=1}a_n\) converge. Si\(\displaystyle \lim_{n→∞}a_n/b_n→∞\), y\(\displaystyle \sum^∞_{n=1}b_n\) diverge, entonces\(\displaystyle \sum^∞_{n=1}a_n\) diverge.