8.8: Serie Taylor

En la Sección 8.6, mostramos cómo ciertas funciones pueden ser representadas por una función de serie de potencia. En 8.7, mostramos cómo podemos aproximar funciones con polinomios, dado que se dispone de suficiente información derivada. En esta sección combinamos estos conceptos: si una función\(f(x)\) es infinitamente diferenciable, mostramos cómo representarla con una función de series de potencia.

Definición 39 series taylor y maclaurin

Dejar\(f(x)\) tener derivados de todos los pedidos en\(x=c\).

1. La serie Taylor de\(f(x)\), centrado en\(c\) es\[\sum_{n=0}^\infty \frac{f\,^{(n)}(c)}{n!}(x-c)^n.\]
2. El ajuste\(c=0\) le da a la Serie Maclaurin de\(f(x)\):\[\sum_{n=0}^\infty \frac{f\,^{(n)}(0)}{n!}x^n.\]

La diferencia entre un polinomio de Taylor y una serie de Taylor es que la primera es un polinomio, que contiene sólo un número finito de términos, mientras que el segundo es una serie, una suma de un conjunto infinito de términos. Al crear el polinomio Taylor de grado\(n\) para una función\(f(x)\) en\(x=c\), necesitábamos evaluar\(f\), y las primeras\(n\) derivadas de\(f\), at\(x=c\) .Al crear la serie Taylor de\(f\), ayuda a encontrar un patrón que describa el\(n^\text{th}\) derivado de\(f\) at\(x=c\) .Demostramos esto en los siguientes dos ejemplos.

Ejemplo\(\PageIndex{1}\): The Maclaurin series of \(f(x) = \cos x\)

Encuentra la serie Maclaurin de\(f(x)=\cos x\).

Solución
En el Ejemplo 8.7.4 encontramos el\(8^\text{th}\) grado Maclaurin polinomio de.Al hacerlo, creamos la tabla que se muestra en la Figura 8.29.\(\cos x\)

Figura 8.29: Una tabla de los derivados de\(f(x)= \cos x\) evaluados at\(x=0\).

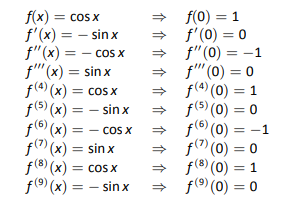
Observe cómo\(f\,^{(n)}(0)=0\) cuándo\(n\) es impar,\(f\,^{(n)}(0)=1\) cuándo\(n\) es divisible por\(4\), y\(f\,^{(n)}(0)=-1\) cuándo\(n\) es par pero no divisible por 4. Así, la serie Maclaurin de\(\cos x\) es

\[1-\frac{x^2}2+\frac{x^4}{4!}-\frac{x^6}{6!}+\frac{x^8}{8!} - \cdots\]

Podemos ir más allá y escribir esto como una suma. Como solo necesitamos los términos donde el poder de\(x\) es par, escribimos la serie power en términos de\(x^{2n}\):

\[\sum_{n=0}^\infty (-1)^{n}\frac{x^{2n}}{(2n)!}.\]

Ejemplo\(\PageIndex{2}\): The Taylor series of \(f(x)=\ln x\) at \(x=1\)

Encuentra la serie Taylor de\(f(x) = \ln x\) centrado en\(x=1\).

Solución
La Figura 8.30 muestra la\(n^\text{th}\) derivada de\(\ln x\) evaluada a\(x=1\) for\(n=0,\ldots,5\), junto con una expresión para el\(n^\text{th}\) término:\[f\,^{(n)}(1) = (-1)^{n+1}(n-1)!\quad \text{for \(n\geq 1\).}\] Recuerde que esto es lo que distingue a las series Taylor de los polinomios Taylor; estamos muy interesados en encontrar un patrón para el\(n^\text{th}\) término, no solo encontrar un conjunto finito de coeficientes para un polinomio.

Figura 8.30: Derivados de\(\ln x\) evaluados en\(x=1\).

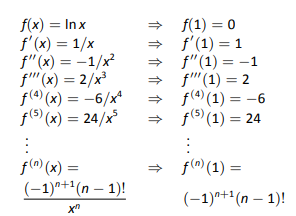
Ya que\(f(1) = \ln 1 = 0\), nos saltamos el primer trimestre y comenzamos la suma con\(n=1\), dando la serie Taylor para\(\ln x\), centrado en\(x=1\), como

\[\sum_{n=1}^\infty (-1)^{n+1}(n-1)!\frac{1}{n!}(x-1)^n = \sum_{n=1}^\infty (-1)^{n+1}\frac{(x-1)^n}{n}. \]

Es importante señalar que la Definición 39 define una serie de Taylor dada una función\(f(x)\); sin embargo, aún no podemos afirmar que\(f(x)\) sea igual a su serie Taylor. Encontraremos que “la mayoría de las veces” son iguales, pero hay que considerar las condiciones que nos permitan concluir esto.

El teorema 76 afirma que el error entre una función\(f(x)\) y\(n^\text{th}\) su polinomio de Taylor de grado\(p_n(x)\) es\(R_n(x)\), donde

\[ \big|R_n(x)\big| \leq \frac{\max\left|\,f\,^{(n+1)}(z)\right|}{(n+1)!}\big|(x-c)^{(n+1)}\big|.\]

Si\(R_n(x)\) va a 0 para cada uno\(x\) en un intervalo a\(I\) medida que\(n\) se acerca al infinito, concluimos que la función es igual a su expansión de la serie Taylor.

teorema 77 función y taylor series igualdad

Dejar\(f(x)\) tener derivados de todos los órdenes en\(x=c\), dejar\(R_n(x)\) ser como se afirma en el Teorema 76, y dejar que\(I\) sea un intervalo en el que\(f(x)\) converja la serie Taylor de.

Si\(\lim\limits_{n\to\infty} R_n(x) = 0\) para todos\(x\) en\(I\), entonces\[f(x) = \sum_{n=0}^\infty \frac{f\,^{(n)}(c)}{n!}(x-c)^n\ \text{ on \(I\).}\]

Demostramos el uso de este teorema en un ejemplo.

Ejemplo\(\PageIndex{3}\): Establishing equality of a function and its Taylor series

Mostrar que\(f(x) = \cos x\) es igual a su serie Maclaurin, como se encuentra en el Ejemplo 8.8.1, para todos\(x\).

Solución

Dado un valor\(x\), la magnitud del término de error\(R_n(x)\) está limitada por

\[ \big|R_n(x)\big| \leq \frac{\max\left|\,f\,^{(n+1)}(z)\right|}{(n+1)!}\big|x^{n+1}\big|.\]

Ya que todas las derivadas de\(\cos x\) son\(\pm \sin x\) o\(\pm\cos x\), cuyas magnitudes están delimitadas por\(1\), podemos afirmar

\[ \big|R_n(x)\big| \leq \frac{1}{(n+1)!}\big|x^{n+1}\big|\]

lo que implica

\[ -\frac{|x^{n+1}|}{(n+1)!} \leq R_n(x) \leq\frac{|x^{n+1}|}{(n+1)!}.\label{eq:coseqtaylor}\]

Para cualquier\(x\),\(\lim\limits_{n\to\infty} \frac{x^{n+1}}{(n+1)!} = 0\). Aplicando el Teorema de Squeeze a la Ecuación\ ref {eq:coseqtaylor}, concluimos que\( \lim\limits_{n\to\infty} R_n(x) = 0\) para todos\(x\), y por lo tanto

\[\cos x = \sum_{n=0}^\infty (-1)^{n}\frac{x^{2n}}{(2n)!}\quad \text{for all \(x\)}.\]

Es natural suponer que una función es igual a su serie Taylor en el intervalo de convergencia de la serie, pero este no es el caso. Para establecer adecuadamente la igualdad, se debe utilizar el Teorema 77. Esto es un poco decepcionante, ya que desarrollamos bellas técnicas para determinar el intervalo de convergencia de una serie de potencias, y demostrar que\(R_n(x)\to 0\) puede ser engorroso ya que trata de derivadas de alto orden de la función.

Hay buenas noticias. Una función\(f(x)\) que es igual a su serie Taylor, centrada en cualquier punto del dominio de\(f(x)\), se dice que es una función analítica, y la mayoría, si no todas, las funciones que encontramos dentro de este curso son funciones analíticas. En términos generales, cualquier función que se cree con funciones elementales (polinomios, exponenciales, funciones trigonométricas, etc.) que no esté definida por partes es probablemente analítica. Para la mayoría de las funciones, asumimos que la función es igual a su serie Taylor en el intervalo de convergencia de la serie y solo usamos el Teorema 77 cuando sospechamos que algo puede no funcionar como se esperaba.

Desarrollamos la serie Taylor para una función más importante, luego damos una tabla de la serie Taylor para una serie de funciones comunes.

Ejemplo\(\PageIndex{4}\): The Binomial Series

Encuentra la serie Maclaurin de\(f(x) = (1+x)^k\),\(k\neq 0\).

Solución

Cuando\(k\) es un entero positivo, la serie Maclaurin es finita. Por ejemplo, cuando\(k=4\), tenemos

\[f(x) = (1+x)^4 = 1+4x+6x^2+4x^3+x^4.\]

Los coeficientes de\(x\) cuando\(k\) es un entero positivo se conocen como los coeficientes binomiales, dando su nombre a la serie que estamos desarrollando.

Cuando\(k=1/2\), tenemos\(f(x) = \sqrt{1+x}\) .Conocer una representación en serie de esta función daría una manera útil de aproximarse\(\sqrt{1.3}\), por ejemplo.

Para desarrollar la serie Maclaurin\(f(x) = (1+x)^k\) para cualquier valor de\(k\neq0\), consideramos los derivados de\(f\) evaluados en\(x=0\):

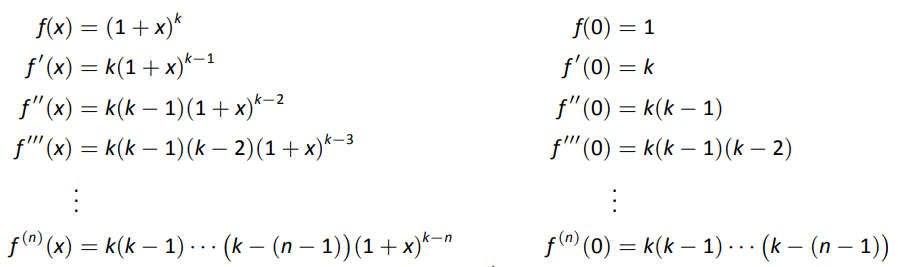
Así la serie Maclaurin para\(f(x) = (1+x)^k\) es

\[1+ k + \frac{k(k-1)}{2!} + \frac{k(k-1)(k-2)}{3!} + \ldots + \frac{k(k-1)\cdots\big(k-(n-1)\big)}{n!}+\ldots\]

Es importante determinar el intervalo de convergencia de esta serie. Con

\[a_n = \frac{k(k-1)\cdots\big(k-(n-1)\big)}{n!}x^n,\]

aplicamos la Prueba de Ratio:

\ [\ begin {alinear*}
\ lim\ límites_ {n\ a\ infty}\ frac {|a_ {n+1} |} {|a_n|} &=\ lim\ limits_ {n\ a\ infty}\ izquierda|\ frac {k (k-1)\ cdots (k-n)} {(n+1)!} x^ {n+1}\ derecha|\ Big/\ izquierda|\ frac {k (k-1)\ cdots\ grande (k- (n-1)\ grande)} {n!} x^n\ derecha|\\
&=\ lim\ límites_ {n\ a\ infty}\ izquierda|\ frac {k-n} {n} x\ derecha|\\
&= |x|.
\ end {alinear*}\]

La serie converge absolutamente cuando el límite de la Prueba de Relación es menor a 1; por lo tanto, tenemos convergencia absoluta cuando\(|x|<1\).

Mientras que fuera del alcance de este texto, el intervalo de convergencia depende del valor de\(k\) .Cuando\(k>0\), el intervalo de convergencia es\([-1,1]\) .Cuando\(-1<k<0\), el intervalo de convergencia es\([-1,1)\) .Si\(k\leq -1\), el intervalo de convergencia es\((-1,1)\).

Aprendimos que los polinomios de Taylor ofrecen una manera de aproximar una función “difícil de calcular” con un polinomio. Las series Taylor ofrecen una manera de representar exactamente una función con una serie. Probablemente se pueda ver el uso de una buena aproximación; ¿hay algún uso de representar una función exactamente como una serie?

Si bien no debemos pasar por alto la belleza matemática de la serie Taylor (que es razón suficiente para estudiarlas), también hay usos prácticos. Proporcionan una valiosa herramienta para resolver una variedad de problemas, incluyendo problemas relacionados con la integración y ecuaciones diferenciales.

En Key Idea 32 (en la siguiente página) damos una tabla de la serie Taylor de una serie de funciones comunes. Luego damos un teorema sobre el “álgebra de series de poder”, es decir, cómo podemos combinar series de potencia para crear series de poder de nuevas funciones. Esto nos permite encontrar la serie Taylor de funciones como\(f(x) = e^x\cos x\) conociendo la serie Taylor de\(e^x\) y\(\cos x\).

Antes de investigar la combinación de funciones, considere la serie Taylor para la función arcangente (ver Idea clave 32). Sabiendo eso\(\tan^{-1}(1) = \pi/4\), podemos utilizar esta serie para aproximar el valor de\(\pi\):

\ [\ begin {align}
\ frac {\ pi} 4 &=\ tan^ {-1} (1) = 1-\ frac13+\ frac15-\ frac17+\ frac19-\ cdots\\
\ pi &= 4\ izquierda (1-\ frac13+\ frac15-\ frac17+\ frac19-\ cdots\ derecha)
\ end align {}\]

Desafortunadamente, esta expansión particular de\(\pi\) converge muy lentamente. Los primeros 100 términos\(\pi\) se aproximan como\(3.13159\), lo cual no es particularmente bueno.

CLAVE IDEA 32 IMPORTANTES EXPASIONES SERIE

TEORAMA 78 ALGEBRA DE PODER SERIE

Dejar\( f(x) = \sum_{n=0}^\infty a_nx^n\) y\( g(x) = \sum_{n=0}^\infty b_nx^n\) converger absolutamente para\(|x|<R\), y dejar que\(h(x)\) sea continuo.

1. \( f(x)\pm g(x) = \sum_{n=0}^\infty (a_n\pm b_n)x^n\)\ quad para\(|x|<R\).
2. \( f(x)g(x) = \left(\sum_{n=0}^\infty a_nx^n\right)\left(\sum_{n=0}^\infty b_nx^n\right) = \sum_{n=0}^\infty\big(a_0b_n+a_1b_{n-1}+\ldots a_nb_0\big)x^n \text{ for }|x|<R\).
3. \( f\big(h(x)\big) = \sum_{n=0}^\infty a_n\big(h(x)\big)^n \quad \text{ for }|h(x)|<R\).

Ejemplo\(\PageIndex{5}\): Combining Taylor series

Escribe los primeros 3 términos de la Serie Taylor para\(f(x) = e^x\cos x\) usar Key Idea 32 y Teorema 78.

Solución

Key Idea 32 nos informa que

\[e^x = 1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots\quad \text{and}\quad \cos x = 1-\frac{x^2}{2!}+\frac{x^4}{4!}+\cdots.\]

Aplicando el Teorema 78, encontramos que

\ (\ begin {align}
e^x\ cos x &=\ left (1+x+\ frac {x^2} {2!} +\ frac {x^3} {3!} +\ cdots\ derecha)\ izquierda (1-\ frac {x^2} {2!} +\ frac {x^4} {4!} +\ cdots\ derecha). \\
\ text {Distribuir} &\ text {la expresión de la mano derecha a través de la izquierda:}\\
&= 1\ left (1-\ frac {x^2} {2!} +\ frac {x^4} {4!} +\ cdots\ derecha) +x\ izquierda (1-\ frac {x^2} {2!} +\ frac {x^4} {4!} +\ cdots\ derecha) +\ frac {x^2} {2!} \ left (1-\ frac {x^2} {2!} +\ frac {x^4} {4!} +\ cdots\ derecha)\\
&+\ frac {x^3} {3!} \ left (1-\ frac {x^2} {2!} +\ frac {x^4} {4!} +\ cdots\ derecha) +\ frac {x^4} {4!} \ left (1-\ frac {x^2} {2!} +\ frac {x^4} {4!} +\ cdots\ right) +\ cdots\\
&\ text {Distribuir de nuevo y recopilar términos similares.} \\
&= 1 + x -\ frac {x^3} {3} -\ frac {x^4} {6} -\ frac {x^5} {30} +\ frac {x^7} {630} +\ cdots
\ end {align}\)

Si bien este proceso es un poco tedioso, es mucho más rápido que evaluar todas las derivadas necesarias\(e^x\cos x\) y calcular directamente la serie Taylor.

Debido a que la serie para\(e^x\) y\(\cos x\) ambas convergen\((-\infty,\infty)\), también lo hace la expansión de la serie para\(e^x\cos x\).

Ejemplo\(\PageIndex{6}\): Creating new Taylor series

Utilice el Teorema 78 para crear series para\(y=\sin(x^2)\) y\(y=\ln (\sqrt{x})\).

Solución
Dado que

\[\sin x = \sum_{n=0}^\infty (-1)^n\frac{x^{2n+1}}{(2n+1)!} = x-\frac{x^3}{3!}+\frac{x^5}{5!} -\frac{x^7}{7!}+\cdots,\]

simplemente\(x^2\) sustituimos\(x\) en la serie, dando

\[\sin (x^2) = \sum_{n=0}^\infty (-1)^n\frac{(x^2)^{2n+1}}{(2n+1)!} = x^2-\frac{x^6}{3!}+\frac{x^{10}}{5!} -\frac{x^{14}}{7!}\cdots.\]

Dado que la serie Taylor para\(\sin x\) tiene un radio infinito de convergencia, también lo hace la serie Taylor para\(\sin(x^2)\).

La expansión de Taylor para\(\ln x\) dado en Key Idea 32 se centra en\(x=1\), así que centraremos la serie para\(\ln (\sqrt{x})\) at\(x=1\) también.
Con

\[\ln x = \sum_{n=1}^\infty(-1)^{n+1}\frac{(x-1)^n}{n} = (x-1)- \frac{(x-1)^2}{2} +\frac{(x-1)^3}{3}-\cdots,\]

sustituimos\(\sqrt{x}\)\(x\) para obtener

\[\ln (\sqrt{x}) = \sum_{n=1}^\infty(-1)^{n+1}\frac{(\sqrt{x}-1)^n}{n} = (\sqrt{x}-1)- \frac{(\sqrt{x}-1)^2}{2} +\frac{(\sqrt{x}-1)^3}{3}-\cdots.\]

Si bien esto no es estrictamente una serie de potencias, es una serie que nos permite estudiar la\(\ln(\sqrt{x})\) función.Dado que el intervalo de convergencia de\(\ln x\) es\((0,2]\), y el rango de\(\sqrt{x}\) on\((0,4]\) es\((0,2]\), el intervalo de convergencia de esta serie de expansión de\(\ln(\sqrt{x})\) es\((0,4]\).

Nota: En el Ejemplo 8.8.6, se podría crear una serie para simplemente reconociéndolo\(\ln(\sqrt{x}) = \ln (x^{1/2}) = 1/2\ln x\), y\(\ln(\sqrt{x})\) por lo tanto multiplicando la serie Taylor\(\ln x\) por por\(1/2\) .Este ejemplo se eligió para demostrar otros aspectos de las series, como el hecho de que el intervalo de convergencia cambia.

Ejemplo\(\PageIndex{7}\): Using Taylor series to evaluate definite integrals

Utilice la serie Taylor de\(e^{-x^2}\) para evaluar\( \int_0^1e^{-x^2}\ dx\).

Solución

Aprendimos, al estudiar Integración Numérica, que\(e^{-x^2}\) no tiene un antiderivado expresable en términos de funciones elementales. Esto significa que cualquier integral definida de esta función debe tener su valor aproximado, y no computado exactamente.

Podemos escribir rápidamente la serie Taylor por\(e^{-x^2}\) usar la serie Taylor de\(e^x\):

\ [\ begin {alinear*}
e^x &=\ suma_ {n=0} ^\ infty\ frac {x^n} {n!} = 1+x+\ frac {x^2} {2!} +\ frac {x^3} {3!} +\ cdots\\
\ texto {y así} &\\
e^ {-x^2} &=\ sum_ {n=0} ^\ infty\ frac {(-x^2) ^n} {n!} \\
&=\ suma_ {n=0} ^\ infty (-1) ^n\ frac {x^ {2n}} {n!} \\
&= 1-x^2+\ frac {x^4} {2!} -\ frac {x^6} {3!} +\ cdots.
\ end {alinear*}\]

Utilizamos el Teorema 75 para integrar:

\[\int e^{-x^2}\ dx = C + x - \frac{x^3}{3}+\frac{x^5}{5\cdot2!}-\frac{x^7}{7\cdot3!}+\cdots +(-1)^n\frac{x^{2n+1}}{(2n+1)n!}+\cdots\]

Esta es la antiderivada de\(e^{-x^2}\); si bien podemos escribirla como una serie, no podemos escribirla en términos de funciones elementales. Podemos evaluar la integral definida\( \int_0^1e^{-x^2}\ dx\) usando este antiderivado; sustituyendo 1 y 0 por\(x\) y restando da

\[\int_0^1e^{-x^2}\ dx = 1-\frac{1}{3}+\frac{1}{5\cdot 2!}-\frac{1}{7\cdot3!} + \frac{1}{9\cdot4!}\cdots.\]

Sumando los 5 términos mostrados anteriormente dan la aproximación de\(0.74749.\) Dado que se trata de una serie alterna, podemos utilizar el Teorema de Aproximación de Serie Alternante, (Teorema 71), para determinar qué tan precisa es esta aproximación. El siguiente término de la serie es\( 1/(11\cdot5!) \approx 0.00075758\) .Así sabemos que nuestra aproximación está dentro\(0.00075758\) del valor real de la integral. Esto es posiblemente mucho menos trabajo que usar la Regla de Simpson para aproximar el valor de la integral.

Ejemplo\(\PageIndex{8}\): Using Taylor series to solve differential equations

Resolver la ecuación diferencial\(y^{\prime}=2y\) en términos de una serie de potencias, y utilizar la teoría de la serie Taylor para reconocer la solución en términos de una función elemental.

Solución

Encontramos los primeros 5 términos de la solución de series de potencia a esta ecuación diferencial en el Ejemplo 8.6.5 en la Sección 8.6. Estos son:

\[a_0=1,\quad a_1 = 2,\quad a_2 = \frac42=2,\quad a_3=\frac{8}{2\cdot3}=\frac43,\quad a_4=\frac{16}{2\cdot3\cdot4} = \frac23.\]

Incluimos las expresiones “no simplificadas” para los coeficientes que se encuentran en el Ejemplo 8.6.5 ya que estamos buscando un patrón. Se puede demostrar que\(a_n = 2^n/n!\) .Así, la solución, escrita como una serie de potencia, es

\[y = \sum_{n=0}^\infty \frac{2^n}{n!}x^n = \sum_{n=0}^\infty \frac{(2x)^n}{n!}.\]

Usando la Idea Clave 32 y el Teorema 78, reconocemos\(f(x) = e^{2x}\):

\[e^x = \sum_{n=0}^\infty \frac{x^n}{n!} \qquad \Rightarrow \qquad e^{2x} = \sum_{n=0}^\infty \frac{(2x)^n}{n!}.\]

Encontrar un patrón en los coeficientes que coincidan con la expansión en serie de una función conocida, como los mostrados en la Idea Clave 32, puede ser difícil. ¿Y si los coeficientes del ejemplo anterior se dieran en su forma reducida? ¿Cómo podríamos recuperar aún la función\(y=e^{2x}\)?

Supongamos que todo lo que sabemos es que

\[a_0=1,\quad a_1=2,\quad a_2=2,\quad a_3=\frac43,\quad a_4=\frac23.\]

La definición 39 establece que cada término de la expansión Taylor de una función incluye una.\(n!\) Esto nos permite decir que

\[a_2=2=\frac{b_2}{2!},\quad a_3 = \frac43=\frac{b_3}{3!},\quad \text{and}\quad a_4 = \frac23=\frac{b_4}{4!}\]

para algunos valores\(b_2\),\(b_3\) y\(b_4\).

Resolviendo por estos valores, vemos eso\(b_2=4\),\(b_3 = 8\) y\(b_4=16\) .Es decir, estamos recuperando el patrón que habíamos visto anteriormente, permitiéndonos escribir

\ [\ comenzar {alinear*}
f (x) =\ suma_ {n=0} ^\ infty a_nx^n &=\ suma_ {n=0} ^\ infty\ frac {b_n} {n!} x^n\\
&= 1+2x+\ frac {4} {2!} x^2 +\ frac {8} {3!} x^3+\ frac {16} {4!} x^4 +\ cdots
\ final {alinear*}\]

A partir de aquí es más fácil reconocer que la serie está describiendo una función exponencial.

Hay formas más simples y directas de resolver la ecuación diferencial.\(y^{\prime} = 2y\) Aplicamos técnicas de series de potencia a esta ecuación para demostrar su utilidad, y pasamos a mostrar cómo a veces somos capaces de recuperar la solución en términos de funciones elementales usando la teoría de Taylor serie. La mayoría de las ecuaciones diferenciales que se enfrentan en situaciones científicas y de ingeniería reales son mucho más complicadas que esta, pero las series de potencia pueden ofrecer una valiosa herramienta para encontrar, o al menos aproximar, la solución.

Este capítulo introdujo secuencias, que son listas ordenadas de números, seguidas de series, en las que sumamos los términos de una secuencia. Rápidamente vimos que tales sumas no siempre suman “infinito”, sino que convergen. Estudiamos pruebas de convergencia, luego terminamos el capítulo con una forma formal de definir funciones a partir de series. Estas “funciones definidas en serie” son una herramienta valiosa para resolver una serie de problemas diferentes a lo largo de la ciencia y la ingeniería.

En los próximos capítulos hay nuevas formas de definir curvas en el plano además de usar funciones de la forma\(y=f(x)\). Las curvas creadas por estos nuevos métodos pueden ser hermosas, útiles e importantes.

Colaboradores y Atribuciones

• Template:ContribApexCalc