7.1: Relaciones Binarias

Recordemos que, por definición, cualquier función\(f : A \rightarrow B\) es un conjunto de pares ordenados. Más precisamente, cada elemento de\(f\) es un par ordenado\((a, b)\), tal que\(a \in A\) y\(b \in B\). Por lo tanto, cada elemento de\(f\) es un elemento de\(A \times B\), así\(f\) es un subconjunto de\(A \times B\). \[\text { Every function from } A \text { to } B \text { is a subset of } A \times B \text {. }\]

Ejemplo\(7.1.1\).

La función\(\text {mother: PEOPLE } \rightarrow \text { PEOPLE }\) está representada por el conjunto\[\{(p, m) \in \text { PEOPLE } \times \text { PEOPLE } \mid m \text { is the mother of } p\} .\]

Muchas otras relaciones también pueden ser representadas por subconjuntos de\(\text {PEOPLE } \times \text { PEOPLE}\), aunque no sean funciones. Por ejemplo, el hijo no es una función, porque algunas personas tienen más de un hijo (o porque algunas personas no tienen hijos en absoluto). Sin embargo, podemos representar esta relación por el conjunto\[\{(p, s) \in \text { PEOPLE } \times \text { PEOPLE } \mid s \text { is a son of } p\} .\]

De hecho, cualquier relación que puedas definir entre dos personas (o, por decirlo así en el lenguaje oficial de la lógica, cualquier predicado binario en el conjunto\(\text {PEOPLE}\)) puede ser representada por un subconjunto de\(\text {PEOPLE } \times \text { PEOPLE}\). Algunos ejemplos de posibles relaciones son:

• \(x\)es hermana de\(y\)
• \(x\)sabía\(y\) en la secundaria
• \(x\)es más alto que\(y\)
• \(x\)y\(y\) están en la misma clase de matemáticas
• etc.

En reconocimiento de esto, los matemáticos simplemente definen una relación como un conjunto de pares ordenados; es decir, una relación es cualquier subconjunto de\(A \times B\). A diferencia del caso de las funciones, no hay restricciones — cada subconjunto es una relación.

Definición\(7.1.2\).

Supongamos\(A\) y\(B\) son conjuntos.

1. Cualquier subconjunto de\(A \times B\) se llama relación de\(A\) a\(B\).
2. Para el caso especial donde\(A = B\), cualquier subconjunto de\(A \times A\) se llama una relación binaria on\(A\).

Nos preocuparemos principalmente por las relaciones binarias, no las relaciones de un conjunto\(A\) a otro conjunto\(B\).

Ejemplo\(7.1.3\).

Algunos ejemplos de relaciones binarias\(\text {PEOPLE}\) son:\(\text {brother, sister, aunt, uncle, mother, father, grandfather, cousin, etc.}\)

Definición\(7.1.4\).

Podemos dibujar una imagen para representar cualquier relación binaria dada en cualquier conjunto dado\(A\):

• Dibuja un punto para cada elemento de\(A\).
• Para\(a, b \in A\), dibuja una flecha de\(a\) a\(b\) si y solo si\((a, b)\) es un elemento de la relación.

La imagen resultante se llama dígrafo. (La palabra se pronuncia “Die-graff” — es la abreviatura de “grafo dirigido”.)

Ejemplo\(7.1.5\).

Vamos\(A = \{1, 2, 3, 4, 5\}\). Podemos definir una relación binaria\(R\) en\(A\) dejando\[R=\left\{(x, y) \mid x^{2}+y<10\right\} .\]

Esta relación binaria está representada por el siguiente dígrafo:

Por ejemplo, tenga en cuenta que\((x, 4) \in R \text { iff } x \in\{1,2\}\), y el dígrafo tiene flechas del 1 al 4 y del 2 al 4.

Ejercicio\(7.1.6\).

Deja\(B\) ser el conjunto compuesto por ti, tus hermanos, tus padres y tus abuelos. Dibuja un dígrafo que represente cada una de las siguientes relaciones binarias en\(B\).

1. La relación “alguna vez ha tenido el mismo apellido que”.
2. La relación “es hijo de”.
3. La relación “se ha casado alguna vez”.

Ejemplo\(7.1.7\).

Este libro (como otros libros de texto de matemáticas) trata principalmente de las relaciones sobre conjuntos de objetos matemáticos. Aquí hay algunos ejemplos bien conocidos:

1. La relación menor que “\(<\)” es una relación binaria sobre\(\mathbb{R}\).
   Es decir, para cualquier número real\(x\) y\(y\), la aseveración\(x < y\) es verdadera o falsa.
2. La relación de igualdad “\(=\)” es una relación binaria sobre todo el universo del discurso\(\mathcal{U}\).
3. La relación de subconjunto “\(\subset\)” es una relación binaria en la colección de todos los conjuntos en\(\mathcal{U}\).
4. La relación “\(x\)es disjunta de\(y\)” es también una relación binaria sobre la colección de todos los conjuntos en\(\mathcal{U}\).

Notación\(7.1.8\).

Supongamos que\(R\) es una relación binaria en un conjunto\(A\). Para\(a_{1}, a_{2} \in A\):

1. Para significar eso\((a_{1}, a_{2}) \in R\), podemos escribir\(a_{1} R a_{2}\).
2. Para significar eso\(\left(a_{1}, a_{2}\right) \notin R\), podemos escribir\(a_{1} \not R a_{2}\).

Hay tres propiedades básicas que cualquier relación binaria dada puede tener o no:

Definición\(7.1.9\).

Supongamos que\(R\) es una relación binaria en un conjunto\(A\).

1. Decimos que\(R\) es reflexivo iff\(\forall a \in A,(a R a)\).
2. Decimos que\(R\) es simétrico iff\(\forall a, b \in A,((a R b) \Rightarrow(b R a))\).
3. Decimos que\(R\) es transitivo iff\(\forall a, b, c \in A,(((a R b) \&(b R c)) \Rightarrow(a R c))\).

Ejemplo\(7.1.10\).

1. “\(=\)” es reflexivo, simétrico y transitivo. ”
2. “\(<\)” es transitivo, pero ni reflexivo ni simétrico.
3. “\(\subset\)” es transitivo y reflexivo, pero no simétrico.

Ejemplo\(7.1.12\).

Considere la siguiente relación binaria\(R\) en\(\{1, 2, 3\}\):\[R=\{(1,1),(2,2),(3,3),(1,2),(2,1),(2,3),(3,2)\}\]

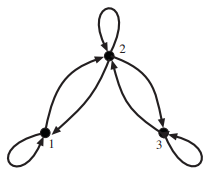
1. \(R\)es reflexivo, porque\(1 R 1,2 R 2,\), y\(3 R 3\).
2. \(R\)es simétrico, porque, para cada uno\((a, b) \in R\), la inversión también\((b, a)\) está en\(R\).
3. \(R\)no es transitivo, porque\(1 R 2\) y\(2 R 3\), pero\(1 \not R 3\).

Ejercicio\(7.1.12\).

Encuentra relaciones binarias sobre\(\{1, 2, 3\}\) eso son:

1. simétricas, pero ni reflexivas ni transitivas.
2. reflexivo, pero ni simétrico ni transitivo.
3. transitivo y simétrico, pero no reflexivo.
4. ni reflexivo, ni simétrico, ni transitivo.

(Exprese cada relación como un conjunto de pares ordenados, dibuje el dígrafo correspondiente y justifique brevemente sus respuestas. )