6.1: Cardinalidad

En este capítulo utilizamos funciones para explorar la idea del tamaño de un conjunto. Los resultados que obtenemos son profundos y muy interesantes, especialmente cuando consideramos la simplicidad de las herramientas que estamos utilizando. Por supuesto, tendremos que usar estas herramientas de alguna manera astutamente.

La teoría de conjuntos viene en diferentes sabores. El más difícil es la teoría de conjuntos axiomática. Muchos resultados interesantes se han derivado en la teoría de conjuntos axiomática formal, pero el tema es avanzado y no es adecuado para una introducción a las matemáticas superiores. En cambio, estudiaremos lo que se llama teoría de conjuntos ingenua. El uso de la palabra “ingenuo” no es peyorativo, sino que pretende diferenciar este enfoque de la teoría de conjuntos axiomática. La mayoría de los matemáticos han estudiado la teoría de conjuntos ingenua, pero relativamente pocos han trabajado extensamente con axiomas de conjuntos.

Cardinalidad

Deseamos comparar el tamaño de los conjuntos. La herramienta fundamental para nuestra investigación es la biyección. En el caso de los conjuntos finitos, que se pueden enumerar exhaustivamente, esto es fácil. Dados dos conjuntos finitos cualesquiera,\(X\) y\(Y\), podríamos enumerar los elementos y contarlos. Siempre que nuestras listas no tengan redundancias, el conjunto más grande es el que tiene el conteo más alto. El acto de enumerar los elementos en un conjunto, donde esto es posible, también es definir una biyección desde un número natural (interpretado como un conjunto) hasta el conjunto que se está contando. La idea de usar funciones para comparar el tamaño de los conjuntos puede generalizarse a conjuntos arbitrarios.

A la hora de comparar el tamaño de los sets infinitos hay intuiciones en competencia. Por un lado tenemos la intuición de que si un conjunto es un subconjunto propio de otro conjunto, debería ser más pequeño. Por otro lado si dos conjuntos son infinitos, ¿cómo puede uno ser más grande que el otro? El uso de biyecciones, inyecciones y suryecciones para definir el tamaño relativo de los conjuntos nos permite ver nuestro camino a través de esta paradoja.

Definición. Equinumero, cardinalidad Dejar\(X\) y\(Y\) ser conjuntos. Eso decimos\(X\) y\(Y\) tenemos la misma cardinalidad si hay una biyección\(f: X \mapsto Y\). Podemos expresar que dos conjuntos tienen la misma cardinalidad por\[|X|=|Y| .\] Si\(|X|=|Y|\), entonces decimos eso\(X\) y\(Y\) son equinumeros.

RECLAMACIÓN. La equinumerosidad es una relación de equivalencia.

(Demostrar esto: Ejercicio 6.2).

Si bien antes de ahora usamos las ideas finitas e infinitas, las definiremos en términos de bijecciones.

DEFINICIÓN. Finito, infinito Let\(X\) be a set. \(X\)es finito si existe alguna\(n \in \mathbb{N}\) y una biyección\(f:\ulcorner n\urcorner \mapsto X\). En el caso de que\(X=\emptyset\), decimos que\(X\) es biyectiva con\(\ulcorner 0\urcorner\) vía la función vacía. Si no\(X\) es finito, decimos que\(X\) es infinito.

Entonces un conjunto es finito si es biyective con un conjunto\(\ulcorner n\urcorner\) para algunos\(n \in \mathbb{N}\). Probablemente no sea de sorprender que un conjunto no pueda ser biyective con diferentes números naturales.

PROPOSICIÓN 6.1. Vamos\(m, n \in \mathbb{N}\). Después\[(|\ulcorner m\urcorner|=|\ulcorner n\urcorner|) \Longleftrightarrow(m=n) .\] Discusión. Demostramos la dirección no trivial de este bicondicional por inducción en uno de los enteros en el enunciado.

PRUEBA. \(\Leftarrow\)

Vamos\(m=n\). Entonces es obvio que\[|\ulcorner m\urcorner|=|\ulcorner n\urcorner| .\]\(\Rightarrow\)

Argumentamos por inducción sobre\(m\).

Caso base:

Si\(m=0\) y\(\left|\left\ulcorner^{n}\right\urcorner\right|=\mid\left\ulcorner_{m}||\right.\) entonces claramente\(n=0\).

Paso de inducción:

Dejemos\(m \in \mathbb{N}\) y supongamos que\[(\forall n \in \mathbb{N})\left[\left|\left\ulcorner^{\prime}\right\urcorner\right|=|\ulcorner\urcorner|\right] \Rightarrow[m=n]\] Demostramos que\[(\forall n \in \mathbb{N})[|\ulcorner m+1\urcorner|=|\ulcorner n\urcorner|] \Rightarrow[m+1=n]\] Supongamos que\[\left|\left\ulcorner^{m}+1\right\urcorner\right|=\left|\left\ulcorner^{\urcorner} n\right\rangle\right|\] Dejemos\[f:\ulcorner m+1\urcorner \longmapsto\ulcorner n\urcorner\] Discusión Una forma natural de proceder con este argumento es restringir el dominio de\(f\) a\(\ulcorner m\urcorner\) y usar la hipótesis de inducción. Desafortunadamente si\(f(m) \neq n-1\) entonces no\(\left.\left.f\right|_{\ulcorner m}\right\urcorner\) es una bijección de\(\ulcorner m\urcorner\) a\(\ulcorner n-1\urcorner\), y la hipótesis de inducción no se aplicará directamente. Para abordar este tema, definiremos una permutación\(g:\ulcorner m+1\urcorner \rightarrow\ulcorner m+1\urcorner\) que reordene los elementos de\(\ulcorner m+1\urcorner\) tal manera que\(f \circ g\) será una biyección satisfactoria\[(f \circ g)(m)=n-1\] Definimos de la\(g:\ulcorner m+1\urcorner \rightarrow\ulcorner m+1\urcorner\) siguiente manera:\[g(x)=\left\{\begin{array}{clc} f^{-1}(n-1) & \text { if } & x=m \\ m & \text { if } \quad x=f^{-1}(n-1) \\ x & & \text { otherwise. } \end{array}\right.\] Vamos \(h=f \circ g\). Entonces\(h\) es una bijección y\[h(m)=(f \circ g)(m)=n-1\]

FIGURA 6.2. Imagen de la permutación\(g\)

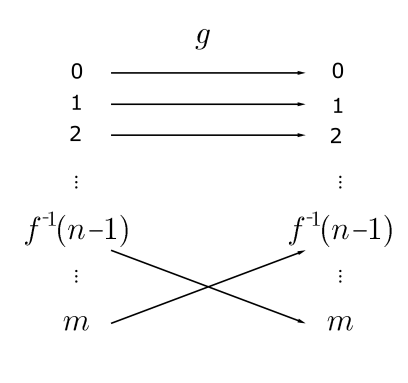
Por lo tanto\[\left.h\right|_{\left\ulcorner_{m}\right\urcorner}:\ulcorner m\urcorner \mapsto\ulcorner n-1\urcorner .\] Por la hipótesis de inducción\[m=n-1 .\]\[m+1=n .\] Por lo tanto Por el principio de inducción,\[(\forall m \in \mathbb{N})(\forall n \in \mathbb{N})(|\ulcorner m\urcorner|=|\ulcorner n\urcorner|) \Rightarrow(m=n) .\] COROLARIO 6.3. Si\(X\) es un conjunto finito, hay exactamente uno\(n \in \mathbb{N}\) tal que\(\ulcorner n\urcorner\) es biyective con\(X\).

Discusión. Este es un argumento de singularidad estándar. Suponemos que un conjunto es biyectiva con números naturales\(\ulcorner n\urcorner\) y\(\ulcorner m\urcorner\), y usamos que la composición de las biyecciones es una biyección para demostrarlo\(m=n\). Esto no es una prueba por contradicción. Más bien estamos demostrando que dos nombres cualesquiera para los números naturales que son biyectivos con\(X\) deben nombrar al mismo número natural. Comprobante. \(X\)es finito, entonces hay\(n \in \mathbb{N}\) tal que\[|X|=|\ulcorner n\urcorner| .\] Let\(m \in \mathbb{N}\) y\[|X|=|\ulcorner m\urcorner| .\] Let\(f: X \mapsto\ulcorner n\urcorner\) y\(g: X \mapsto\ulcorner m\urcorner\). Entonces\(g^{-1}:\ulcorner m\urcorner \mapsto X\). La composición de las biyecciones es una bijección,\[f \circ g^{-1}:\ulcorner m\urcorner \mapsto\ulcorner n\urcorner .\] por lo que Por la Proposición 6.1,\[m=n .\] DEFINICIÓN. Cardinalidad finita Si\(X\) es un conjunto finito, decimos que tiene cardinalidad finita. Dejar\(n \in \mathbb{N}\) ser el número natural único tal que\(\ulcorner n\urcorner\) sea biyective con\(X\). Entonces decimos que\(X\) tiene cardinalidad\(n\), o\[|X|=n \text {. }\] Corolario\(6.3\) garantiza que la cardinalidad de un conjunto finito está bien definida.