6.4: Conjuntos Contables

Los incontables conjuntos que hemos identificado hasta ahora tienen una cierta característica estructural en común. Hemos demostrado que el conjunto de todas las funciones desde un dominio infinito fijo hasta un codominio fijo de al menos dos elementos es incontable. El teorema de Cantor de que el conjunto de poder de un conjunto contable infinito es incontable también se puede interpretar de esta manera. Si\(X\) es un conjunto, entonces se\(P(X)\) puede entender como\(\ulcorner 2\urcorner X\), el conjunto de todas las funciones de\(X\) a\(\ulcorner 2\urcorner\). En el caso de conjuntos finitos,\(X\) y\(Y\), el conjunto de todas las funciones desde\(X\) hasta\(Y, Y^{X}\), tiene cardinalidad\(|Y|^{|X|}\). Es decir, la cardinalidad de\[\{f \subseteq X \times Y \mid f \text { is a function }\}\] es una función exponencial de\(|X|\). Por supuesto, las funciones exponenciales crecen relativamente rápido. Para los conjuntos finitos, la cardinalidad de la unión de conjuntos disjuntos es la suma de las cardinalidades de los conjuntos. La cardinalidad del producto directo de dos conjuntos finitos es producto de las cardinalidades. ¿Qué pasa con la unión o el producto directo de conjuntos infinitos contables? ¿Pueden las operaciones de conjunto de unión y producto directo generar conjuntos incontables a partir de conjuntos contables? Respondemos primero a las preguntas para los sindicatos (adición).

La siguiente proposición simplificará algunos de los detalles técnicos en los argumentos que siguen.

PROPOSICIÓN 6.15. Dejar\(X\) y\(Y\) ser conjuntos. Luego hay una sobrejección\(f: X \rightarrow Y\) iff\(|Y| \leq|X| .\)

Discusión. Utilizaremos los conjuntos de niveles de la sobreyección\(f\) para definir la inyección de\(Y\) a\(X\). Esto utiliza la maquinaria de relaciones de equivalencia desarrollada en el Capítulo 2 con el Axioma de Elección.

Comprobante. \((\Rightarrow)\)

Dejar\(X, Y\) y\(f\) ser como en el enunciado de la proposición. \[\widehat{f}: X / f \rightarrow Y\]Sea la biyección canónica asociada a la\(f\) que se definió en la Sección 2.3. Nos preguntamos si hay una inyección\(g: X / f \rightarrow X\) donde\(g([x]) \in[x]\). Recordemos que\(X / f\) es la colección de subconjuntos de niveles de\(X\), con respecto a\(f\), y es una partición de\(X\). ¿Por qué no simplemente elegir un elemento de cada clase de equivalencia y\(g\) definir como la función de\(X / f\) a\(X\) definida por estas elecciones?

DISCUSIÓN. El Axioma de Elección es la afirmación de que existen tales funciones de “elección”.

La función\(g\) es claramente una inyección, también lo\[g \circ \widehat{f}^{-1}: Y \rightarrow X\] es una inyección. Por lo tanto si hay una sobrejección\(f: X \rightarrow Y\), entonces\(|Y| \leq|X|\).

\((\Leftarrow)\)

La prueba de esta implicación se deja como ejercicio.

TEOREMA 6.16. Teorema de Cantor\(\left\{X_{n} \mid n \in \mathbb{N}\right\}\) Sea una familia de conjuntos tal que\(X_{n}\) sea contable para todos\(n \in \mathbb{N}\), y\(X=\bigcup_{n \in \mathbb{N}} X_{n}\). Después\[|X| \leq \aleph_{0}\] Discusión. Este Teorema, también debido a G. Cantor, es el resultado clave para demostrar que los conjuntos son contables. Se prueba mediante una técnica también llamada argumento diagonal (a veces llamado el primer argumento diagonal). Usamos el conjunto de índices\(\mathbb{N}\) para construir una matriz infinita, y usamos esa matriz para ilustrar una enumeración de la unión. Esta enumeración es una subyección de\(\mathbb{N}\) a\(X\).

PRUEBA. Porque\(n \in \mathbb{N}, X_{n}\) es contable y por Proposición\(6.15\) hay una sobrejección\[f_{n}: \mathbb{N} \rightarrow X_{n}\] Usa las funciones\(f_{n}\) para construir una matriz infinita. La\(0^{\text {th }}\) columna contendrá todos los elementos de\(X_{0}\), en el orden\(f_{0}(0), f_{0}(1), f_{0}(2), \ldots\) (No importa si el mismo elemento se enumera varias veces). La siguiente columna tiene los elementos de\(X_{1}\) en el orden\(f_{1}(0), f_{1}(1), f_{1}(2)\), etc. definimos una función\(g: \mathbb{N} \rightarrow X\) atravesando esta matriz a lo largo de las diagonales noreste a suroeste, a saber\(g(0)=f_{0}(0), g(1)=f_{1}(0), g(2)=\)\(f_{0}(1), g(3)=f_{2}(0), g(4)=f_{1}(1), g(5)=f_{0}(2), g(6)=f_{3}(0)\), y así sucesivamente.

FIGURA 6.17. El primer argumento diagonal

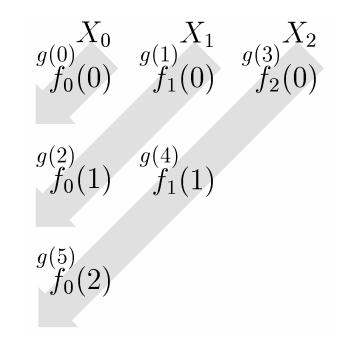
Entonces\(g\) es una sobreyección, porque cada elemento de\(\bigcup X_{n}\) ocurre en la matriz, y por lo tanto está en el rango de\(g\). Por Proposición 6.15,\[|X| \leq \aleph_{0} .\] COROLARIO 6.18. Dejar\(A\) ser un conjunto contable y\(\left\{X_{\alpha} \mid \alpha \in A\right\}\) ser una familia de conjuntos contables indexados por A. Entonces\[\left|\bigcup_{\alpha \in A} X_{\alpha}\right| \leq \aleph_{0} \text {. }\] Prueba. Ya que\(A\) es contable, hay una sobrejección\[f: \mathbb{N} \rightarrow A .\] Por lo tanto\[\bigcup_{\alpha \in A} X_{\alpha}=\bigcup_{n \in \mathbb{N}} X_{f(n)}\] Por el Teorema de Cantor 6.16,\[\left|\bigcup_{\alpha \in A} X_{\alpha}\right| \leq \aleph_{0} .\] COROLARIO 6.19. \(\mathbb{Z}\)es contable.

Discusión. Sin demasiado esfuerzo, podríamos definir una bijección de\(\mathbb{N}\) a\(\mathbb{Z}\). En cambio probaremos la existencia de la biyección sin definir explícitamente una biyección.

Comprobante. \(f: \mathbb{N} \rightarrow \mathbb{Z}\)Sea tal que\[f(n)=-n .\] Entonces\(f[\mathbb{N}]\) sea contable. Por el teorema de Cantor\[\mathbb{Z}=\mathbb{N} \cup f[\mathbb{N}]\] es contable.

Volvemos nuestra atención a los productos directos.

TEOREMA 6.20. Si\(n \in \mathbb{N}\), y\(X_{1}, X_{2}, \ldots, X_{n}\) son conjuntos contables, entonces\[X_{1} \times X_{2} \times \cdots X_{n}\] es contable.

Comprobante. Suponemos que todos los factores, no\(X_{1}, \ldots, X_{n}\) están vacíos. Argumentamos por inducción sobre el número de factores.

Caso base:\(n=2\). \[X_{1} \times X_{2}=\bigcup_{x \in X_{2}} X_{1} \times\{x\}\]Para cada uno\(x \in X_{2}\),\[\left|X_{1}\right|=\left|X_{1} \times\{x\}\right| .\] Por Corolario 6.18,\(X_{1} \times X_{2}\) es contable.

Paso de inducción: Supongamos que para cualquier colección de conjuntos\(n\) contables\(X_{1}, \ldots X_{n}\), el producto\(X_{1} \times \cdots \times X_{n}\) es contable. Let\(X_{1}, \ldots, X_{n+1}\) Ser conjuntos no vacíos contables. Entonces\[X_{1} \times \cdots \times X_{n+1}=\left(X_{1} \times \cdots \times X_{n}\right) \times X_{n+1}\] Por la hipótesis de inducción,\(X_{1} \times \cdots \times X_{n}\) es contable, y por el caso base el producto directo de dos conjuntos contables es contable. Por lo tanto,\(X_{1} \times \cdots \times X_{n+1}\) es contable.

COROLARIO 6.21. \(\mathbb{Q}\)es contable.

Comprobante. Dejar\(f: \mathbb{Z} \times \mathbb{Z} \rightarrow \mathbb{Q}\) ser definido por\[f(a, b)=\left\{\begin{array}{ccc} a / b & \text { if } & b \neq 0 \\ 0 & \text { otherwise. } \end{array}\right.\] Entonces\(f\) es una sobrejección, y por Proposición\(6.15, \mathbb{Q}\) es contable.

Hemos evaluado la secuencia anidada de conjuntos,\[\mathbb{N} \subsetneq \mathbb{Z} \subsetneq \mathbb{Q} \subsetneq \mathbb{R} \text {. }\] Estos son conjuntos matemáticos importantes y, con la excepción de\(\mathbb{R}\), son contables. Investigamos la cardinalidad de un conjunto más entre\(\mathbb{Q}\) y\(\mathbb{R}\).

DEFINICIÓN. Número real algebraico,\(\mathbb{K}\) Un número real\(\alpha\) es algebraico si hay un polinomio\(p\) (no idénticamente 0) con coeficientes enteros tales que\(p(\alpha)=0\). Vamos a denotar el conjunto de todos los números algebraicos por\(\mathbb{K}\).

Cualquier número racional\(a / b \in \mathbb{Q}\) es algebraico, ya que\(a / b\) es una raíz del polinomio\[p(x)=b x-a .\] Además, en el Ejemplo 3.23, demostramos que\(\sqrt{2}\) es irracional, y es claramente algebraico, ya que es una raíz de\(x^{2}-2\). Por lo tanto tenemos\[\mathbb{N} \subsetneq \mathbb{Z} \subsetneq \mathbb{Q} \subsetneq \mathbb{K} \subseteq \mathbb{R} .\] Finalmente lo demostramos\(\mathbb{K} \neq \mathbb{R}\) demostrando que\(\mathbb{K}\) es contable. TEOREMA 6.22. \(\mathbb{K}\)es contable.

Discusión. Este resultado se demuestra mostrando que los números reales algebraicos pueden ser construidos por un procedimiento contable. Es decir,\(\mathbb{K}\) puede construirse agregando a\(\mathbb{Q}\) contablemente muchos elementos a la vez contabilizadamente muchas veces. El Teorema de Cantor implica que cualquier conjunto así construido será contable.

PRUEBA. Dejar\(n \in \mathbb{N}\) y definir\(f: \prod_{i=0}^{n} \mathbb{Z} \rightarrow \mathbb{Z}[x]\)\[f\left(a_{0}, \ldots, a_{n}\right)=\sum_{i=0}^{n} a_{i} x^{i} .\] por Por Corolario 6.19,\(\mathbb{Z}\) es contable. Por Teorema 6.20,\(\prod_{i=0}^{n} \mathbb{Z}\) es contable. El rango de\(f\) es el conjunto de polinomios con coeficientes enteros con grado\(\leq n\) (o el polinomio idénticamente igual a 0). Por Proposición\(6.15\), el rango de una función con un dominio contable también es contable. Por lo tanto, el conjunto de polinomios de grado\(\leq n\) es contable.

Dejar\(P_{n}\) ser el conjunto de polinomios con coeficientes enteros de grado\(\leq n\). Entonces\[\mathbb{Z}[x]=\bigcup_{i=0}^{\infty} P_{n} .\] Por Teorema 6.16,\(\mathbb{Z}[x]\) es contable. Por Teorema 4.10, si\(p(x)\) es un polinomio con coeficientes reales de grado\(n\), tiene a lo sumo raíces\(n\) reales. Let\[Z_{p}=\{\alpha \mid p(\alpha)=0\} .\] So\(Z_{p}\) es finito para cada polinomio\(p\). Aplicar nuevamente el Teorema de Cantor (Teorema 6.16),\[\mathbb{K}=\bigcup_{p \in \mathbb{Z}[x]} Z_{p}\] es contable.

COROLARIO 6.23. \(\mathbb{K} \neq \mathbb{R}\)

Dado que\(\mathbb{K}\) es contable y\(\mathbb{R}\) es incontable,\(\mathbb{K}\) es un subconjunto propio de\(\mathbb{R}\). DEFINICIÓN. Número trascendental Un número real que no es algebraico se llama número trascendental.

Corolario\(6.23\) afirma que hay números trascendentales. Se trata de una pretensión de existencia en la que no se presenta ningún testigo de la demanda. Más bien es un ejemplo de argumento de conteo (sobre conjuntos infinitos). Hay demasiados números reales para que todos sean algebraicos. A finales del siglo XIX se demostró que\(\pi\) y\(e\) son trascendentales, pero estas pruebas son mucho más complicadas que la prueba de existencia de Cantor anterior, que es, en esencia, una aplicación muy inteligente del principio del casillero.

COROLARIO 6.24. Hay incontables muchos números trascendentales.

PRUEBA. \(T\)Sea el conjunto de números trascendentales. Como\[|\mathbb{R}|=|T \cup \mathbb{K}|>\aleph_{0},\] y\(\mathbb{K}\) es contable,\(T\) debe ser incontable.

Por lo que hemos demostrado que\[\mathbb{N} \subsetneq \mathbb{Z} \subsetneq \mathbb{Q} \subsetneq \mathbb{K} \subsetneq \mathbb{R} .\] Sin embargo,\[|\mathbb{N}|=|\mathbb{Z}|=|\mathbb{Q}|=|\mathbb{K}|<|\mathbb{R}|\]