4.1: Introducción a la Inducción

En este capítulo, se introduce la inducción matemática, que es una técnica de prueba que es útil para probar declaraciones de la forma (∀n ∈\(\mathbb{N}\)) P (n), o más generalmente (∀n ∈\(\mathbb{Z}\)) (n ≥ a =⇒ P (n)), donde P (n) es algún predicado y a ∈\(\mathbb{Z}\).

Considerar las reclamaciones:

1. Para todos\(n\in\mathbb{N}\),\(\displaystyle 1+2+3+\cdots +n=\frac{n(n+1)}{2}\).
2. Para todos\(n\in\mathbb{N}\),\(n^{2}+n+41\) es prime.

Echemos un vistazo a las pruebas potenciales.

“Prueba” de (a). Si\(n=1\), entonces\(1=\frac{1(1+1)}{2}\). Si\(n=2\), entonces\(1+2=3=\frac{2(2+1)}{2}\). Si\(n=3\), entonces\(1+2+3=6=\frac{3(3+1)}{2}\), y así sucesivamente.

“Prueba” de (b). Si\(n=1\), entonces\(n^{2}+n+41=43\), cuál es primo. Si\(n=2\), entonces\(n^{2}+n+41=47\), cuál es primo. Si\(n=3\), entonces\(n^{2}+n+41=53\), cuál es primo, y así sucesivamente.

¿Son estas pruebas reales? ¡No! De hecho, la segunda afirmación ni siquiera es cierta. Si\(n=41\), entonces\(n^{2}+n+41=41^{2}+41+41=41(41+1+1)\), que no es primo ya que tiene 41 como factor. Resulta que la primera afirmación es cierta, pero lo que escribimos no puede ser una prueba ya que el mismo tipo de razonamiento cuando se aplica al segundo reclamo parece probar algo que en realidad no es cierto. Necesitamos una forma rigurosa de capturar “y así sucesivamente” y una forma de verificar si realmente es “y así sucesivamente”.

Recordemos que un axioma es una suposición matemática básica. El siguiente axioma es uno de los Axiomas de Peano, que es una colección de axiomas para los números naturales introducidos en el siglo XIX por el matemático italiano Giuseppe Peano (1858—1932).

Axioma 4.1. Que\(S\subseteq \mathbb{N}\) tal que tanto

1. \(1\in S\), y
2. si\(k\in S\), entonces\(k+1\in S\).

Entonces\(S=\mathbb{N}\).

Podemos pensar en el conjunto\(S\) como una escalera, donde la primera hipótesis es decir que tenemos un primer peldaño de una escalera. La segunda hipótesis dice que si estamos en algún peldaño arbitrario de la escalera, entonces siempre podemos llegar al siguiente peldaño. Tomados en conjunto, esto dice que podemos pasar del primer peldaño al segundo, del segundo al tercero, y en general, de cualquier\(k\) th peldaño al\((k+1)\) st peldaño, para que nuestra escalera sea en realidad\(\mathbb{N}\). ¿Estás de acuerdo en que el Axioma de la Inducción es una suposición bastante razonable?

Al final de la Sección 3.2, discutimos brevemente ZFC, que es la elección estándar para la teoría de conjuntos axiomática. Resulta que se puede probar el Axioma de Inducción como teorema en ZFC. No obstante, ese no será el enfoque que adoptemos. En cambio, estamos asumiendo que el Axioma de la Inducción es cierto. Utilizando este axioma, podemos probar el siguiente teorema, conocido como el Principio de Inducción Matemática. Un enfoque para probar este teorema es dejar\(S=\{k\in \mathbb{N}\mid P(k) \text{ is true}\}\) y usar el Axioma de Inducción. El conjunto a veces\(S\) se llama el conjunto de la verdad. Tu trabajo es demostrar que el conjunto de la verdad es todo\(\mathbb{N}\).

Teorema 4.2. Dejar\(P(1), P(2), P(3), \ldots\) ser una secuencia de declaraciones, una por cada número natural. Asumir

1. \(P(1)\)es verdad, y
2. si\(P(k)\) es verdad, entonces\(P(k+1)\) es verdad.

Entonces\(P(n)\) es cierto para todos\(n\in\mathbb{N}\).

El Principio de Inducción Matemática nos proporciona un proceso para probar declaraciones de la forma: “Para todos”\(n\in\mathbb{N}\)\(P(n)\), donde\(P(n)\) hay algún predicado que involucra\(n\). La hipótesis (i) anterior se denomina paso base (o caso base) mientras que (ii) se denomina paso inductivo.

No se debe confundir la inducción matemática con el razonamiento inductivo asociado a las ciencias naturales. El razonamiento inductivo es un método científico mediante el cual se inducen principios generales a partir de observaciones. Por otro lado, la inducción matemática es una forma deductiva de razonamiento utilizada para establecer la validez de una proposición.

Prueba de Esqueleto 4.3. Aquí está la estructura general para una prueba por inducción.

Se procede por inducción.

1. Paso base: [Verifica que\(P(1)\) sea cierto. Esto a menudo, pero no siempre, equivale a\(n=1\) enchufarse en dos lados de alguna ecuación reclamada y que ambos lados son realmente iguales.]
2. Paso inductivo: [Tu objetivo es demostrar “Para todos\(k\in\mathbb{N}\), si\(P(k)\) es verdad, entonces \(P(k+1)\)es verdad”.] Dejemos\(k\in\mathbb{N}\) y supongamos que eso\(P(k)\) es cierto. [Hacer algo para derivar que \(P(k+1)\)sea cierto.] Por lo tanto,\(P(k+1)\) es cierto.

Así, por inducción,\(P(n)\) es cierto para todos\(n\in\mathbb{N}\).

Demostrar los siguientes teoremas usando inducción. El primer resultado puede parecer familiar a partir del cálculo. Recordemos eso\(\displaystyle \sum_{i=1}^{n}i=1+2+3+\cdots +n\), por definición.

Teorema 4.4. Para todos\(n\in\mathbb{N}\),\(\displaystyle \sum_{i=1}^{n}i=\frac{n(n+1)}{2}\).

Teorema 4.5. Para todos\(n\in\mathbb{N}\), 3 divide\(4^{n}-1\).

Teorema 4.6. Para todos\(n\in\mathbb{N}\), 6 divide\(n^{3}-n\).

Teorema 4.7. Let\(p_{1}, p_{2}, \ldots, p_{n}\) Ser\(n\) distintos puntos dispuestos en un círculo. Entonces el número de segmentos de línea que unen todos los pares de puntos es\(\frac{n^{2}-n}{2}\).

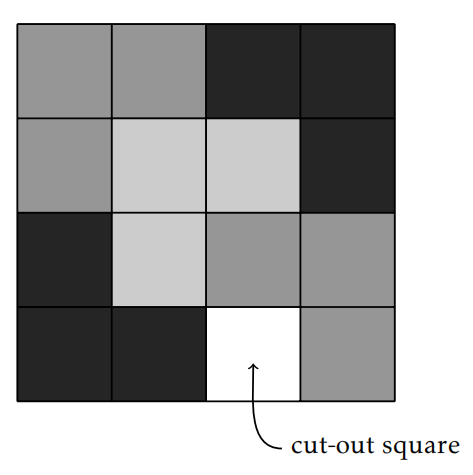
Problema 4.8. Considera una cuadrícula de cuadrados que es\(2^n\) cuadrados de ancho por\(2^n\) cuadrados de largo, donde\(n\in\mathbb{N}\). Una de las plazas ha sido recortada, ¡pero no sabes cuál! Tienes un montón de formas en L compuestas por\(3\) cuadrados. Demuestra que puedes cubrir perfectamente este tablero de ajedrez con las formas en L (sin superposición) para cualquier\(n\in\mathbb{N}\). La Figura 4.1 representa una posible cobertura para el caso que involucra\(n=2\).

Figura 4.1: Una posible cobertura para el caso que involucra n = 2 para el Problema 4.8.