7.1: Relaciones

Si bien no existe una definición universal de matemáticas acordada, se podría argumentar que las matemáticas se centran en el estudio de patrones y relaciones. Ciertos tipos de relaciones ocurren una y otra vez en las matemáticas. Una forma de formalizar la naturaleza abstracta y la estructura de estas relaciones es con la noción de relaciones. En el Capítulo 8, veremos que una función es un tipo especial de relación.

Recordemos de la Sección 3.5 que el producto cartesiano de dos juegos\(A\) y\(B\), escrito\(A\times B\), es el conjunto de todos los pares ordenados\((a,b)\), donde\(a\in A\) y\(b\in B\). Es decir,\(A\times B=\{(a,b)\mid a\in A, b\in B\}\).

Definición 7.1. Dejar\(A\) y\(B\) ser conjuntos. Una relación\(R\) de\(A\) a \(B\)es un subconjunto de\(A \times B\). Si\(R\) es una relación de\(A\) a\(B\) y\((a,b)\in {R}\), entonces decimos que\(a\) está relacionado con \(b\)y podemos escribir\(aR\) \(b\) en lugar de\((a,b)\in{R}\). Si\(R\) es una relación de\(A\) al mismo conjunto\(A\), entonces decimos que\(R\) es una relación sobre \(A\).

Ejemplo 7.2. El conjunto\(\mathbb{N}\times \mathbb{R}\) de Problema 3.55 es un ejemplo de una relación sobre\(\mathbb{R}\) ya que\(\mathbb{N}\times \mathbb{R}\) es un subconjunto de\(\mathbb{R}\times \mathbb{R}\).

Es importante notar que el orden en que escribimos las cosas para las relaciones importa. En particular, si\(R\) es una relación de\(A\) a\(B\) y\(a R b\), entonces puede o no ser así\(bR a\).

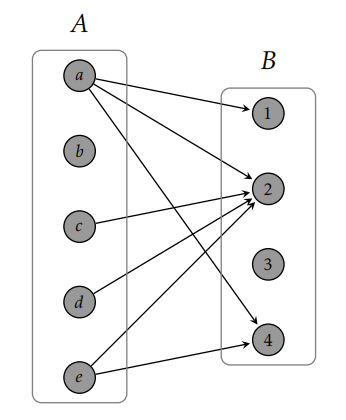
Ejemplo 7.3. Si\(A=\{a,b,c,d,e\}\) y\(B=\{1,2,3,4\}\), entonces el conjunto de pares ordenados\[R=\{(a,1),(a,2),(a,4),(c,2),(d,2),(e,2),(e,4)\}\] es un ejemplo de una relación de\(A\) a\(B\). En este caso, podríamos escribir\((c,2)\in{R}\) o\(cR 2\). También podríamos decir que\(a\) está relacionado con 1, 2 y 4.

Ejemplo 7.4. Al igual que en el ejemplo anterior, vamos\(A=\{a,b,c,d,e\}\). Una posible relación\(A\) está dada por\[R=\{(a,a),(a,b),(a,c),(b,b),(b,a),(b,c),(c,d),(c,e),(d,d),(d,a),(d,c),(e,a)\}.\]

Ejemplo 7.5. Considera el conjunto de cuentas\(A\) en la plataforma de redes sociales Twitter. En Twitter, cada cuenta tiene un conjunto de cuentas que siguen. Podemos modelar esta situación matemáticamente usando una relación sobre\(A\). Definir\(T\) en\(A\) vía\(xTy\) si\(x\) sigue\(y\) en Twitter. Como un conjunto\[T=\{(x,y)\in A\times A\mid x\text{ follows }y\text{ on Twitter}\}.\]

Ejemplo 7.6. Ya estás familiarizado con muchas relaciones. Por ejemplo,\(=\),\(\leq\), y\(<\) son cada uno ejemplos de relaciones sobre los números reales. Podríamos decir que\((3,\pi)\) está en la relación\(\leq\) y la relación\(<\) desde\(3\leq \pi\) y\(3<\pi\). Sin embargo, no\((3,\pi)\) está en la relación\(=\) desde entonces\(3\neq \pi\). También, observe que el orden importa para las relaciones\(\leq\) y\(<\) sin embargo no para\(=\). Por ejemplo,\((-\sqrt{2}, 4)\) está en la relación\(\leq\) mientras no\((4,-\sqrt{2})\) lo está.

Ejemplo 7.7. Definir la relación\(S\) de\(\{-1,1\}\) a\(\mathbb{Z}\) vía\(1Sx\) si\(x\) es par y\(-1Sx\) si\(x\) es impar. Es decir,\(1\) está relacionado con todos los enteros pares y\(-1\) está relacionado con todos los enteros impares.

Ejemplo 7.8. Dejar\(A\) ser cualquier conjunto. Ya que\(\emptyset \subseteq A\times A\), el conjunto vacío forma una relación sobre\(A\). A esta relación se le llama la relación vacía sobre\(A\).

Las relaciones se pueden representar mediante dígrafos. Un dígrafo (abreviatura de gráfico dirigido) es un gráfico discreto que consiste en un conjunto de vértices conectados por aristas, donde los bordes tienen una dirección asociada a ellos. Si\(R\) es una relación de\(A\) a\(B\), entonces los elementos de\(A\) y\(B\) son los vértices del dígrafo y hay un borde dirigido de\(a\in A\) a\(b\in B\) si \((a,b)\)está en la relación\(R\) (i.e.,\(aR b\)). Podemos representar visualmente dígrafos usando puntos para representar los vértices y flechas para representar los bordes dirigidos. No vamos a hacer una distinción entre un dígrafo y su representación visual. Utilizar un dígrafo para representar una relación puede ser poco práctico si hay un gran número de vértices o aristas dirigidas.

Ejemplo 7.9. Consideremos la relación dada en el Ejemplo 7.3. El dígrafo correspondiente se representa en la Figura 7.1. Observe que hemos colocado los vértices correspondientes a elementos de a\(A\) la izquierda y los elementos de a\(B\) la derecha. Esta es una práctica estándar, pero lo que realmente importa son las conexiones de borde no cómo se colocan los vértices en la página.

= [circle, draw, fill=gris, sep=0pt interior=0pt, tamaño mínimo=5mm] = [dibujar, -stealth]

Problema 7.10. Dejar\(A=\{1,2,3,4,5,6\}\)\(B=\{1,2,3,4\}\) y definir\(D\) de\(A\) a\(B\) vía\((a,b)\in D\) si\(a-b\) es divisible por 2. Enumere los pares ordenados\(D\) y dibuje el dígrafo correspondiente.

Si\(R\) es una relación on\(A\) (es decir, una relación de\(A\) a\(A\)), entonces podemos simplificar la estructura del dígrafo utilizando solo una copia de\(A\) para los vértices. En este caso, es posible que hayamos dirigido bordes que apunten desde un vértice a sí mismo. Al dibujar dígrafos para una relación en un conjunto, se utilizará por defecto este dígrafo simplificado (como el representado en la Figura 7.2 (b)).

Ejemplo 7.11. La Figura 7.2 (a) representa la relación del Ejemplo 7.4 como un dígrafo de\(A\) a\(A\) mientras que el dígrafo de la Figura 7.2 (b) proporciona una representación aerodinámica de la misma relación que utiliza los elementos en una\(A\) sola vez en lugar de dos veces.

Problema 7.12. Dejar\(A=\{1,2,3,4,5,6\}\) y definir\(|\) en\(A\) vía\(x|y\) si\(x\) divide\(y\). Enumere los pares ordenados\(|\) y dibuje el dígrafo correspondiente.

Figura 7.1: Dígrafo para una relación de A = {a, b, c, d, e} a B = {1,2,3,4}.

Figura 7.2: Dos variaciones de dígrafos para una relación en A = {a, b, c, d, e}.

Problema 7.13. Dejar\(A=\{a,b,c,d\}\) y definir\(R\) en\(A\) via\[{R}=\{(a,a),(a,b),(a,c),(b,b),(b,a),(b,c),(c,c),(c,a),(c,b),(d,d)\}.\]

1. Dibuja el dígrafo para\(R\).
2. Dibuja el dígrafo para la relación vacía en\(A\).

También podemos representar visualmente una relación trazando los puntos en la relación. En particular, si\(R\) es una relación de\(A\) a\(B\) y\(aR b\), podemos trazar todos los puntos\((a,b)\) que satisfagan\(aR b\) en dos dimensiones, donde interpretamos el conjunto\(A\) como el eje horizontal y\(B\) para ser el eje vertical. Nos referiremos a esta representación visual de una relación como la gráfica de la relación.

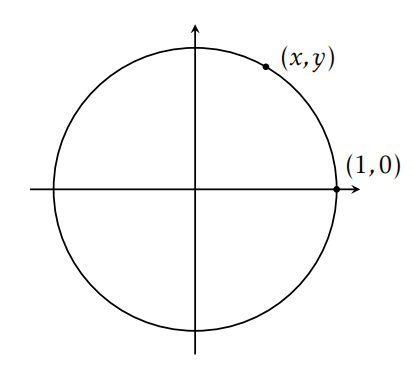
Ejemplo 7.14. Cuando escribimos\(x^2+y^2=1\), estamos definiendo implícitamente una relación. En particular, la relación es el conjunto de pares ordenados\((x,y)\) satisfactorios\(x^2+y^2=1\), a saber\(\{(x,y)\in \mathbb{R}^2 \mid x^2+y^2=1\}\). La gráfica de esta relación en\(\mathbb{R}^2\) es el círculo unitario centrado en el origen en el plano como se muestra en la Figura 7.3.

Figura 7.3: Gráfico de la relación determinada por x ² + y ² = 1.

Problema 7.15. Para cada una de las siguientes, dibuje una porción de la gráfica que represente la relación como un subconjunto de\(\mathbb{R}^2\).

1. \(\{(x,y)\in \mathbb{R}^2 \mid y=x^2\}\)
2. \(\{(x,y)\in \mathbb{Z}^2 \mid y=x^2\}\)
3. \(\{(x,y)\in \mathbb{R}^2 \mid y^2=x\}\)
4. \(\{(x,y)\in \mathbb{N}\times \mathbb{R} \mid y^2=x\}\)

Problema 7.16. Dibuja una porción de la gráfica que represente la relación\(\leq\) en\(\mathbb{R}\).

Para una relación sobre un conjunto, es natural considerar la colección de elementos con los que se relaciona un elemento dado. Por ejemplo, la “Lista de seguimiento” de un usuario en Twitter es el conjunto de cuentas en Twitter que el usuario está siguiendo.

Definición 7.17. Que\(R\) sea una relación en un set\(A\). Para cada uno\(a\in A\), definimos el conjunto de familiares de\(a\) con respecto a \(R\)vía También\[rel(a,R):= \{b\in A\mid aR b\}.\] definimos la colección de los conjuntos de familiares con respecto a \(R\)por\[Rel(R):= \{rel(a)\mid a\in A\}.\]

Si\(R\) es claro desde el contexto, usualmente escribiremos\(rel(a)\) en lugar de\(rel(a,R)\). En cuanto a dígrafos,\(rel(a)\) es la colección de vértices que tienen un borde dirigido apuntando hacia ellos desde el vértice etiquetado por\(a\). En la teoría gráfica, esta colección de vértices se llama el vecindario out de\(a\) y cada vértice se llama un vecino out. Observe que\(Rel(R)\) es un conjunto de conjuntos. En particular, un elemento en\(Rel(R)\) es un subconjunto de\(A\) —equivalentemente, un elemento de\(\mathcal{P}(A)\).

Problema 7.18. Consideremos la relación dada en el Ejemplo 7.4. Al inspeccionar los pares ordenados en\(R\) o al mirar el dígrafo en la Figura 7.2 (b), vemos eso\[rel(a) = \{a,b,c\},\ rel(b) = \{a,b,c\},\ rel(c) = \{d,e\},\ rel(d) = \{a,c,d\},\ rel(e) = \{a\},\] así que\(Rel(R) = \{\{a,b,c\},\{d,e\},\{a,c,d\},\{a\}\}\).

Problema 7.19. Considerar la relación dada en el Problema 7.13 (a). Encuentra\(Rel(R)\) determinando\(rel(x)\) para cada uno\(x\in A\).

Problema 7.20. Describir la colección de los conjuntos de familiares respecto a la relación vacía del Problema 7.13 (b).

Problema 7.21. Vamos a\(P\) denotar el conjunto de todas las personas con cuentas en Facebook y definir la relación\(F\) en\(P\) vía\(xFy\) si\(x\) es amigo de\(y\). Describa\(rel(\text{Maria})\), donde María es el nombre de un usuario específico de Facebook. ¿Qué es\(Rel(F)\)?

Problema 7.22. Definir la relación\(\equiv_5\) en\(\mathbb{Z}\) via\(a\equiv_5 b\) si\(a-b\) es divisible por 5. Encontrar\(rel(1)\),\(rel(2)\), y\(rel(6)\). ¿En cuántos conjuntos distintos hay\(Rel(\equiv_5)\)? Enumere los distintos conjuntos en\(Rel(\equiv_5)\).

Problema 7.23. Considerar la relación\(\leq\) sobre\(\mathbb{R}\). Si\(x\in \mathbb{R}\), ¿qué es\(rel(x)\)?

Problema 7.24. Supongamos que\(R\) es una relación sobre\(A=\{1,2,3,4,5\}\) tal que\(rel(1)=\{1,3,4\}\)\(rel(2)=\{4\}\),\(rel(3)=\{3,4,5\}\),\(rel(4)=\{1,2\}\),, y\(rel(5)=\emptyset\). Enumere los pares ordenados\(R\) y dibuje el dígrafo correspondiente.

Ahora examinaremos tres propiedades importantes que una relación en un conjunto puede o no poseer.

Definición 7.25. Que\(R\) sea una relación en un set\(A\).

1. La relación\(R\) es reflexiva si es para todos\(a\in A\),\(aR a\).
2. La relación\(R\) es simétrica si para todos\(a,b\in A\), si\(aR b\), entonces\(bR a\).
3. La relación\(R\) es transitiva si para todos\(a,b,c\in A\), si\(aR b\) y\(bR c\), entonces\(aR c\).

Ejemplo 7.26. Aquí hay algunos ejemplos que ilustran los conceptos en la definición anterior.

1. La relación\(=\)\(\mathbb{R}\) es reflexiva, simétrica y transitiva.
2. La relación\(\leq\) es reflexiva y transitiva\(\mathbb{R}\), pero no simétrica. Sin embargo, observe que\(<\) es transitivo\(\mathbb{R}\), pero ni simétrico ni reflexivo.
3. Si\(S\) es un conjunto, entonces\(\subseteq\) on\(\mathcal{P}(S)\) es reflexivo y transitorio, pero no simétrico.

Problema 7.27. Determinar si las relaciones dadas en cada una de las siguientes son reflexivas, simétricas o transitivas.

1. Ejemplo 7.4
2. Problema 7.13

Problema 7.28. Supongamos que\(R\) es una relación en un conjunto\(A\).

1. Explique lo que significa\(R\) para no ser reflexivo.
2. Explique lo que significa\(R\) para no ser simétrico.
3. Explique lo que significa\(R\) para no ser transitivo.

Problema 7.29. Vamos\(A=\{a,b,c,d,e\}\).

1. Definir una relación\(R\)\(A\) que sea reflexiva pero no simétrica ni transitiva.
2. Definir una relación\(S\)\(A\) que sea simétrica pero no reflexiva ni transitiva.
3. Definir una relación\(T\)\(A\) que sea transitiva pero no reflexiva ni simétrica.

Problema 7.39. Dada una relación\(R\) sobre un conjunto finito\(A\), describir cómo se ve cada uno de reflexivo, simétrico y transitivo en términos de un dígrafo. Es decir, dibujar cuadros que representen cada uno de los reflejos, simétricos y transitivos. Una cosa a tener en cuenta es que los elementos utilizados en las definiciones de simétrico y transitivo no tienen por qué ser distintos. Entonces, es posible que deba considerar varios casos.

A continuación, proporcionamos pruebas esqueléticas para demostrar que una relación es reflexiva, simétrica o transitiva. Observe que la prueba esqueleto para demostrar que una relación es reflexiva es un caso especial de Prueba Esqueleto 2.81. De igual manera, las pruebas esqueléticas que involucran simétricas y transitivas son ambos casos especiales de Prueba Esqueleto 2.82. Es importante señalar que toda relación en el conjunto vacío es vacuamente reflexiva, simétrica y transitiva. En las pruebas esqueléticas a continuación, estamos asumiendo implícitamente que el conjunto en cuestión no está vacío. En algunas circunstancias, puede ser necesario mencionar la posibilidad del conjunto vacío.

Prueba de Esqueleto 7.31. Aquí está la estructura general para demostrar que una relación es reflexiva.

Asumir\(R\) es una relación sobre\(A\) definida por (o satisfactoria)... [Utilizar la definición dada (o describir la propiedad dada) de\(R\)]. Vamos\(a\in A\).

\(\ldots\)[Usar la definición (o propiedad) de\(R\) para verificar que\(aR a\)]\(\ldots\)

Por lo tanto, la relación\(R\) es reflexiva\(A\).

Prueba de Esqueleto 7.32. Aquí está la estructura general para demostrar que una relación es simétrica.

Asumir\(R\) es una relación sobre\(A\) definida por (o satisfactoria)... [Utilizar la definición dada (o describir la propiedad dada) de\(R\)]. Dejemos\(a, b\in A\) y supongamos\(aR b\).

\(\ldots\)[Usar la suposición de que\(aR b\) con definición (o propiedad) de\(R\) verificar que\(bR a\)]\(\ldots\)

Por lo tanto, la relación\(R\) es simétrica sobre\(A\).

Prueba de Esqueleto 7.33. Aquí está la estructura general para demostrar que una relación es transitiva.

Asumir\(R\) es una relación sobre\(A\) definida por (o satisfactoria)... [Utilizar la definición dada (o describir la propiedad dada) de\(R\)]. Dejemos\(a, b, c\in A\) y supongamos\(aR b\) y\(bR c\).

\(\ldots\)[Usar la suposición de que\(aR b\) y\(bR c\) con definición (o propiedad) de\(R\) verificar que\(aR c\)]\(\ldots\)

Por lo tanto, la relación\(R\) es transitiva en\(A\).

Problema 7.34. Determinar si cada una de las siguientes relaciones es reflexiva, simétrica o transitiva. En cada caso, debe proporcionar un contraejemplo específico o una prueba.

1. Consideremos la relación\(T\) descrita en el Ejemplo 7.5.
2. Consideremos la relación\(F\) descrita en Problema 7.21.
3. Consideremos la relación\(\equiv_5\) descrita en Problema 7.22.
4. Dejar\(P\) ser el conjunto de todas las personas y definir\(H\) vía\(xHy\) si\(x\) y\(y\) tienen la misma altura.
5. Dejar\(P\) ser el conjunto de todas las personas y definir\(T\) vía\(xTy\) si\(x\) es más alto que\(y\).
6. Considerar la relación “divide” en\(\mathbb{N}\).
7. Dejar\(L\) ser el conjunto de líneas y definir\(||\) vía\(l_1||l_2\) si\(l_1\) es paralelo a\(l_2\).
8. Dejar\(C[0,1]\) ser el conjunto de funciones continuas encendidas\([0,1]\). Definir\(f\sim g\) si\[\int_0^1|f(x)|\ dx=\int_0^1|g(x)|\ dx.\]
9. Definir\(R\) en\(\mathbb{N}\) vía\(nR m\) si\(n+m\) es par.
10. Definir\(D\) en\(\mathbb{R}\) vía\((x,y)\in D\) si\(x=2y\).
11. Definir\(F\) en\(\mathbb{Z}\times \left(\mathbb{Z}\setminus \{0\}\right)\) vía\((a,b)F(c,d)\) si\(ad=bc\). ¿Reconoces esta relación? Piensa en fracciones.
12. Definir\(\sim\) en\(\mathbb{R}^2\) vía\((x_1,y_1)\sim (x_2,y_2)\) si\(x_1^2+y_1^2=x_2^2+y_2^2\).
13. Definir\(S\) en\(\mathbb{R}\) via\(xS y\) if\(\lfloor x\rfloor =\lfloor y\rfloor\), donde\(\lfloor x\rfloor\) es el mayor entero menor o igual a\(x\) (por ejemplo,\(\lfloor \pi\rfloor=3\),\(\lfloor -1.5\rfloor=-2\), y\(\lfloor 4\rfloor=4\)).
14. Definir\(C\) en\(\mathbb{R}\) vía\(xCy\) si\(|x-y|<1\).