8.5: Funciones reales continuas

En esta sección, exploraremos el concepto de continuidad, que probablemente encontraste en la preparatoria.

Definición 8.95. Una función real es cualquier función\(f:A\to \mathbb{R}\) tal que\(A\) sea un subconjunto no vacío de\(\mathbb{R}\).

Existen varias definiciones equivalentes de continuidad para funciones reales. La siguiente caracterización se conoce típicamente como la definición épsilon-delta de continuidad. Nuestra definición imita la definición de continuidad utilizada en espacios métricos, que\(\mathbb{R}\) dotados de valor absoluto pasa a ser un ejemplo de. Recordemos que\(|a-b|<r\) significa que la distancia entre\(a\) y\(b\) es menor que\(r\) (ver discusión a continuación Corolario 5.31).

Definición 8.96. Supongamos que\(f\) es una función real tal que\(a\in dom(f)\). Decimos que\(f\) es continuo en \(a\)si por cada\(\varepsilon>0\), existe\(\delta>0\) tal que si\(x\in dom(f)\) y\(|x-a|<\delta\), entonces\(|f(x)-f(a)|<\varepsilon\). Si\(f\) es continuo en cada punto de\(B\subseteq dom(f)\), entonces decimos que\(f\) es continuo en \(B\). Si\(f\) es continuo en todo su dominio, simplemente decimos que\(f\) es continuo.

Hablando vagamente, una función real\(f\) es continua en el punto\(a\in dom(f)\) si podemos\(f(x)\) acercarnos arbitrariamente\(f(a)\) al considerar todo\(x\in dom(f)\) lo suficientemente cercano a\(a\). El valor\(\varepsilon\) indica qué tan cerca\(f(a)\) tenemos que estar mientras el valor\(\delta\) está proporcionando la “ventana” alrededor\(a\) necesaria para garantizar que todos los puntos en la ventana (y en el dominio) rindan salidas dentro de \(\varepsilon\)de\(f(a)\). La Figura 8.5 ilustra nuestra definición de continuidad. Obsérvese que en la figura, el punto\(a\) es fijo mientras necesitamos considerar todos\(x\in dom(f)\) tales que\(|x-a|<\delta\). El cuadro discontinuo en la figura tiene dimensiones\(2\delta\) por\(2\varepsilon\) y está centrado en el punto\((a,f(a))\). Intuitivamente, la función es continua en\(a\) ya que dado\(\varepsilon>0\), podríamos encontrar\(\delta >0\) para que la gráfica de la función nunca salga de la parte superior o inferior de la caja discontinua.

Quizás te hayas encontrado con la frase “una función es continua si puedes dibujar su gráfica sin levantar tu lápiz”. Si bien esta descripción proporciona cierta intuición sobre lo que significa la continuidad de una función, no es ni lo suficientemente precisa ni precisa para captar el significado de continuidad.

Al probar que una función es continua en un punto, la elección de\(\delta\) depende tanto del punto en cuestión como del valor de\(\varepsilon\). Un ejemplo debería ser útil.

Ejemplo 8.97. Definir\(f:\mathbb{R}\to\mathbb{R}\) vía\(f(x)=3x+2\). Demostremos que\(f\) es continuo (en cada punto del dominio). Dejar\(a\in\mathbb{R}\) y dejar\(\varepsilon>0\). Elige\(\delta=\varepsilon/3\). Veremos en un momento por qué esta es una buena opción para\(\delta\). Supongamos\(x\in\mathbb{R}\) tal que\(|x-a|<\delta\). Vemos que\[|f(x)-f(a)|=|(3x+2)-(3a+2)|=|3x-3a| = 3\cdot |x-a|<3\cdot \delta = 3\cdot \varepsilon/3 =\varepsilon.\] Hemos demostrado que\(f\) es continuo en\(a\), y desde que\(a\) fue arbitrario,\(f\) es continuo.

Problema 8.98. Demostrar que cada una de las siguientes funciones reales es continua utilizando la Definición 8.96.

Figura 8.5: Representación visual de la continuidad de f en a.

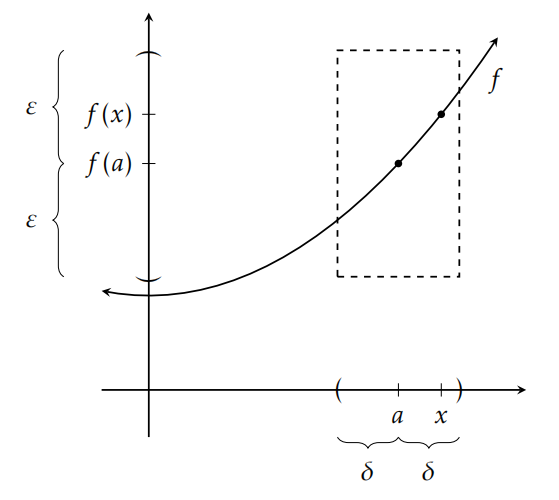
1. \(f:\mathbb{R}\to \mathbb{R}\)definido vía\(f(x)=x\).
2. \(g:\mathbb{R}\to \mathbb{R}\)definido vía\(g(x)=x+42\).
3. \(h:\mathbb{R}\to \mathbb{R}\)definido vía\(h(x)=5x\).

El siguiente resultado nos dice que cada función real lineal es continua. No olvide manejar el caso cuando esté\(m=0\) en su comprobante. Tenga en cuenta que el caso cuando\(m=0\) demuestra que cada función constante es continua.

Teorema 8.99. Si\(f:\mathbb{R}\to\mathbb{R}\) se define vía\(f(x)=mx+b\) for\(m,b\in\mathbb{R}\), entonces\(f\) es continuo.

La segunda parte del siguiente problema es mucho más difícil de lo que cabría esperar.

Problema 8.100. Definir\(f:\mathbb{R}\to\mathbb{R}\) vía\(f(x)=x^2\).

1. Demostrar que\(f\) es continuo a 0.
2. Demostrar que\(f\) es continuo a 1.

Problema 8.101. Definir\(f:\mathbb{R}\to\mathbb{R}\) vía\(f(x)=\sqrt{x}\). Demostrar que\(f\) es continuo a 0.

Problema 8.102. Supongamos que\(f\) es una función real. Escribir una declaración precisa de lo que significa\(f\) para no ser continuo en\(a\in dom(f)\).

Problema 8.103. Defina\(f:\mathbb{R}\to\mathbb{R}\) vía\[f(x)=\begin{cases} 1, & \text{if }x=0\\ x, & \text{otherwise}. \end{cases}\] Determinar dónde\(f\) es continuo y justifica tu afirmación.

Problema 8.104. Defina\(f:\mathbb{R}\to\mathbb{R}\) vía\[f(x)=\begin{cases} 1, & \text{if }x\in \mathbb{Q}\\ 0, & \text{otherwise}. \end{cases}\] Determinar dónde\(f\) es continuo y justifica tu afirmación.

Después de completar el siguiente problema, reflexiona sobre la afirmación “una función es continua si puedes dibujar su gráfica sin levantar tu lápiz”.

Problema 8.105. Definir\(f:\mathbb{N}\to\mathbb{R}\) vía\(f(x)=1\). ¡Observe el dominio! Determina dónde\(f\) es continuo y justifica tu afirmación.

Teorema 8.106. Supongamos que\(f\) es una función real. Entonces\(f\) es continuo si y solo si la preimagen\(f^{-1}(U)\) de cada conjunto abierto\(U\) es un conjunto abierto intersectado con el dominio de\(f\).

La caracterización previa de la continuidad suele ser referida como la “definición de continuidad de conjunto abierto”, aunque para nosotros es un teorema en lugar de una definición. Esta es la definición utilizada en topología. Otra noción de continuidad, llamada “continuidad secuencial”, hace uso de secuencias convergentes. Todas estas caracterizaciones de continuidad son equivalentes para los números reales (utilizando la definición estándar de un conjunto abierto). Sin embargo, hay contextos en matemáticas donde la definición épsilon-delta de continuidad es indefinida (porque no existe una noción de distancia ni en el dominio ni en el codominio) y otros donde la continuidad y continuidad secuencial no son equivalentes.

Dado que cada conjunto abierto es la unión de intervalos abiertos acotados (Definición 5.53), la unión de conjuntos abiertos es abierta (Teorema 5.58), y las preimágenes respetan las uniones (Teorema 8.92), podemos fortalecer el Teorema 8.106 en un resultado un poco más útil.

Teorema 8.107. Supongamos que\(f\) es una función real. Entonces\(f\) es continuo si y solo si la preimagen\(f^{-1}(I)\) de cada intervalo abierto delimitado\(I\) es un conjunto abierto intersectado con el dominio de\(f\).

Ahora que tenemos dos métodos para verificar la continuidad (Definición 8.96 y Teorema 8.106/8.107), puede usar cualquiera de ellos al acercarse a los problemas restantes en esta sección. A veces no importa qué enfoque tomes y otras veces un método podría ser más adecuado para la tarea.

Problema 8.108. Definir\(f:\mathbb{R}\to\mathbb{R}\) vía\(f(x)=x^2\). Demostrar que\(f\) es continuo.

Problema 8.109. Definir\(f:\mathbb{R}\setminus\{0\}\to\mathbb{R}\) vía\(f(x)=\frac{1}{x}\). Determina dónde\(f\) es continuo y justifica tu afirmación.

Los problemas anteriores vuelven a cuestionar la frase “una función es continua si puedes dibujar su gráfica sin levantar el lápiz”.

Problema 8.110. Encuentra una función real continua\(f\) y un intervalo abierto\(I\) tal que la preimagen no\(f^{-1}(I)\) sea un intervalo abierto.

Para los siguientes problemas, si intentas construir contraejemplos, puedes confiar en tus conocimientos previos sobre diversas funciones que encontraste en la secundaria y el cálculo.

Problema 8.111. Supongamos que\(f\) es una función real continua. Si\(U\) hay un conjunto abierto contenido en\(dom(f)\), ¿la imagen\(f(U)\) siempre está abierta? Si es así, demuéstralo. De lo contrario, proporcione un contraejemplo.

Problema 8.112. Supongamos que\(f\) es una función real continua. Si\(C\) es un conjunto cerrado, ¿la preimagen es\(f^{-1}(C)\) siempre un conjunto cerrado? Si es así, demuéstralo. De lo contrario, proporcione un contraejemplo.

Problema 8.113. Supongamos que\(f\) es una función real continua. Si\([a,b]\) está contenido en un intervalo cerrado\(dom(f)\), ¿la imagen es\(f([a,b])\) siempre un intervalo cerrado? Si es así, demuéstralo. De lo contrario, proporcione un contraejemplo.

Problema 8.114. Supongamos que\(f\) es una función real continua. Si un conjunto cerrado\(C\) está contenido en\(dom(f)\), ¿la imagen es\(f(C)\) siempre un conjunto cerrado? Si es así, demuéstralo. De lo contrario, proporcione un contraejemplo.

Problema 8.115. Supongamos que\(f\) es una función real continua. Si\(B\) está contenido en el conjunto delimitado\(dom(f)\), ¿la imagen es\(f(B)\) siempre un conjunto delimitado? Si es así, demuéstralo. De lo contrario, proporcione un contraejemplo.

Problema 8.116. Supongamos que\(f\) es una función real continua. Si\(B\) es un conjunto acotado, ¿la preimagen es\(f^{-1}(B)\) siempre un conjunto acotado? Si es así, demuéstralo. De lo contrario, proporcione un contraejemplo.

Problema 8.117. Supongamos que\(f\) es una función real continua. Si\(K\) es un conjunto compacto, ¿la preimagen es\(f^{-1}(B)\) siempre un conjunto compacto? Si es así, demuéstralo. De lo contrario, proporcione un contraejemplo.

Problema 8.118. Supongamos que\(f\) es una función real continua. Si\(C\) un conjunto conectado está contenido en\(dom(f)\), ¿la imagen\(f(C)\) siempre está conectada? Si es así, demuéstralo. De lo contrario, proporcione un contraejemplo.

Problema 8.119. Supongamos que\(f\) es una función real continua. Si\(C\) es un conjunto conectado, ¿la preimagen es\(f^{-1}(C)\) siempre un conjunto conectado? Si es así, demuéstralo. De lo contrario, proporcione un contraejemplo.

Quizás notó la ausencia de una pregunta natural en la secuencia anterior de problemas. Si\(f\) es una función real continua y\(K\) es un subconjunto del dominio de\(f\), ¿la imagen es\(f(K)\) un conjunto compacto? Resulta que la respuesta es “sí”, pero probar este hecho está más allá del alcance de este libro. Este teorema a menudo se prueba en un curso de análisis real y luego se utiliza para probar el Teorema del Valor Extremo, que puede haber encontrado en su curso de cálculo.

El siguiente resultado es un caso especial del conocido Teorema del Valor Intermedio, que establece que si\(f\) es una función real continua cuyo dominio contiene el intervalo\([a,b]\), entonces\(f\) alcanza cada valor entre\(f(a)\) y \(f(b)\)en algún momento dentro del intervalo\([a,b]\). Para probar el caso especial, utilizar el Teorema 5.87 y el Problema 8.118 junto con una prueba por contradicción.

Teorema 8.120. Supongamos que\(f\) es una función real. Si\(f\) es continuo en\([a,b]\) tal que\(f(a)<0<f(b)\) o\(f(a)>0>f(b)\), entonces existe\(r\in [a,b]\) tal que\(f(r)=0\).

Si generalizamos el resultado anterior, obtenemos el Teorema del Valor Intermedio.

Teorema 8.121. Supongamos que\(f\) es una función real. Si\(f\) es continuo en\([a,b]\) tal que\(f(a)<c<f(b)\) o\(f(a)>c>f(b)\) para algunos\(c\in \mathbb{R}\), entonces existe\(r\in [a,b]\) tal que\(f(r)=c\).

Problema 8.122. ¿Es cierto lo contrario del Teorema del Valor Intermedio? Si es así, demuéstralo. De lo contrario, proporcione un contraejemplo.