2.3: Notas al pie

Última actualización
Guardar como PDF

Page ID: 109803

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Como en el caso del “álgebra” vamos a pretender por el momento saber qué es una “ecuación”. El análisis del presente texto pronto permitirá comprender en qué sentido los problemas babilónicos antiguos pueden entenderse como ecuaciones.

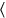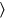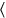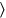“ya alt ves alt ” traduce ta - alt mar alt . El escriba así no omite una palabra, utiliza la primera sílaba (que pasa a llevar la información sobre la persona gramatical) como logograma para toda la palabra. Esto es muy común en los textos de Susa, e ilustra que el uso de los logogramas está vinculado al género textual: solo en los textos matemáticos podemos estar razonablemente seguros de que ningún otro verbo que comience con la sílaba ta estará presente en esta posición.

Un triángulo rectángulo ciertamente también está determinado por una longitud y una anchura (las patas del ángulo recto), y estas dos magnitudes bastan para determinarlo (el tercer lado, si aparece, puede ser “la longitud larga”). Pero un triángulo siempre se introduce como tal. Si no es prácticamente correcto, el texto dará un boceto.

Se debe tomar nota de la palabra “prácticamente”. Los babilonios no tenían ningún concepto del ángulo como una cantidad medible, por lo tanto, nada correspondiente a nuestro “ángulo de”\(78^{\circ}\). Pero distinguían claramente los ángulos “buenos” de los “malos”; podemos usar el juego de palabras de que lo opuesto a un ángulo recto era un ángulo equivocado. Un ángulo recto es aquel cuyas patas determinan un área, ya sea las patas del ángulo recto en un triángulo rectángulo, los lados de un rectángulo, o la altura y la base promedio de un trapecio derecho.

“Simple” porque también hay una “doble posición falsa” que puede servir para resolver problemas de primer grado más complejos. Consiste en hacer dos hipótesis para la solución, que luego se “mezclan” (como en problemas de aleación) de tal manera que los dos errores se cancelan entre sí (en términos modernos, esta es una forma particular de hacer una interpolación lineal). Dado que los babilonios nunca hicieron uso de esta técnica, una “posición falsa” siempre se refiere a la “simple posición falsa” en lo que sigue.

El presente documento emplea muchos logogramas sin complementos fonéticos ni gramaticales. Basta escrito en acadio silábico, sin embargo, para permitirnos discernir el esquema habitual que, en consecuencia, se impone a la traducción.

La palabra sumeria é.dub.ba significa “tablilla”, es decir, “escuela”.